船舶推力轴承弹性支承的轴系纵振减振性能研究
何江洋,何 琳,徐 伟,李正民
(1.海军工程大学 振动与噪声研究所,武汉 430033;2.船舶振动噪声重点实验室,武汉 430033)
船舶推力轴承弹性支承的轴系纵振减振性能研究
何江洋1,2,何 琳1,2,徐 伟1,2,李正民1,2
(1.海军工程大学 振动与噪声研究所,武汉 430033;2.船舶振动噪声重点实验室,武汉 430033)
运用结构弹性波理论,以推力轴承及其弹性支承系统作为一端边界条件,建立推进轴系纵向振动理论模型,详细推导轴系纵向振动特征频率方程,基于泰勒级数展开得到轴系纵振一阶固有频率估算解析式;结合某型船舶参数,重点对比研究集成隔振系统与RC支承子系统对轴系纵振衰减效果,分析结果表明:集成隔振系统能够在较大频段内有效衰减轴系纵向振动,而RC支承子系统表现动力吸振特性;在保证轴系运行安全性的基础上,增大集成隔振系统质量或减小RC支承子系统质量有助于扩大减振频段。
弹性波理论;推力轴承;弹性支承;纵振减振性能
RC(Resonance Charger)
0 引 言
船舶艉部机械噪声一直是低转速船舶的主要噪声源,近年来我国自主研制了浮筏隔振系统、智能气囊隔振装置,成功解决了艉部大型动力设备减振降噪难题。然而推力轴承振动成为新的短板,这也是我国减振降噪急需突破的关键技术之一。推力轴承振动是轴系纵向振动的延伸,由推进器在船舶艉部不均匀流场中运转产生的脉动力引起,某型船舶实测结果表明推力轴承在14 Hz、28 Hz和56 Hz具有较高的振动幅值,分别对应螺旋桨叶频及倍叶频,其低频分布特点引发船舶较强声辐射特征[1],因此,必须采取有效技术手段进行控制。
但推力轴承作为船舶推进系统中重要组成部件,对其控制必须以保证轴系安全运行为前提,工程上多在轴系上串联纵振减振器,受轴系纵向允许变形量的限制,纵振减振器刚度不能过低,对推力轴承低频振动减振效果有限,因此具有低频率、大刚度特点的控制系统成为解决推力轴承振动的关键。
早在上世纪中叶,国外学者对该问题开展了研究,其中Goodwin[2]在1960年提出的Resonance Charger(简称RC,如图1(a)所示),推力瓦块采用液压活塞支承,受螺旋桨推力时,互连的各液压油腔通过外接软管将液压油挤进蓄能器,依靠蓄能器中油液的微小可压缩性衰减轴系纵向振动,具有设计参数取值范围大、适装性好等特点。文献[3]表明该装置已装备国外新型舰船,通过对RC参数优化设计,结果表明轴系纵振一阶固有频率由55 Hz转换至16 Hz,取得了一定的减振效果,但无RC的实测报告,国内对该问题还处在理论研究阶段。
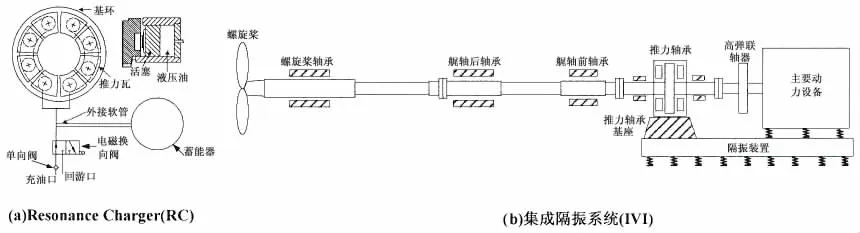
图1 推力轴承振动的控制措施Fig.1 The control measures of thrust bearing’s vibration
此外,针对直接传动的短轴系而言,文献[4]提出的船舶推力轴承及动力设备集成隔振系统(如图1(b)所示),将艉部主要动力设备及推力轴承集成安装在同一大型公共筏体上,分别在筏体垂向、纵向、横向分布低固有频率、横向大刚度高性能元器件,可构成低频大刚度隔振系统,不仅能够有效衰减推力轴承和动力设备振动,同时系统受螺旋桨推力变形较小,保证船舶推进安全性。
本文针对以上两种推力轴承控制措施,以轴系纵向振动为切入点,将RC与集成隔振系统简化为推力轴承端的支承子系统,运用结构弹性波理论,建立轴系纵振理论模型,详细推导轴系纵振特征频率方程,对比研究RC与集成隔振系统对轴系纵振减振性能。
1 轴系纵振理论模型
船舶轴系纵向振动,其力学特征符合一维杆特性,故可将轴系纵向振动类比为有限长杆的纵振。
对于有限长杆,受简谐激励力作用下,作用点会分别产生向两边传播的强迫行进波,遇杆端经反射形成两列自由行进波,如图2所示,根据线性理论及叠加原理,杆上任意点纵向位移可近似地由四列波表示[5-6]:

图2 杆内纵向弹性波示意图Fig.2 The scheme of longitudinal elastic wave in bars

其中:A1、A2为波幅系数,由初始条件与边界条件确定;x0为简谐力作用位置;F0为简谐力激励幅值;E为弹性模量;S为横截面积;kn为纵向振动的波数,k1=-k2=jkL;kL=ω/c,ω为轴系纵振圆频率,c为纵向波传播速度;j为虚数单位;an为纵向振动系统受集中力响应函数系数:

螺旋桨及推力轴承简化为集中质量作为两端边界条件,忽略各支承轴承约束作用,推力轴承支承子系统简化为弹簧振子系统与推力轴承相连:集成隔振系统简化为大质量、低频率、纵向大刚度支承子系统,如图3(a)所示;引用文献[2]中对RC的建模方法,如图3(b)所示。

图3 轴系纵振简化模型Fig.3 The simplified model of shafting longitudinal vibration
图中:F0ejωt为螺旋桨脉动力,作用在螺旋桨端;Mp、Mt、Mg为螺旋桨及其附连水质量、推力轴承及其基座质量、支承子系统质量;Kt、Kg为推力轴承及其基座纵向当量刚度、支承子系统刚度。
零初始条件下(1)式中波幅系数A1、A2由两端边界条件确定,对质量块Mt运用达朗贝尔原理,化简可得两端边界条件:
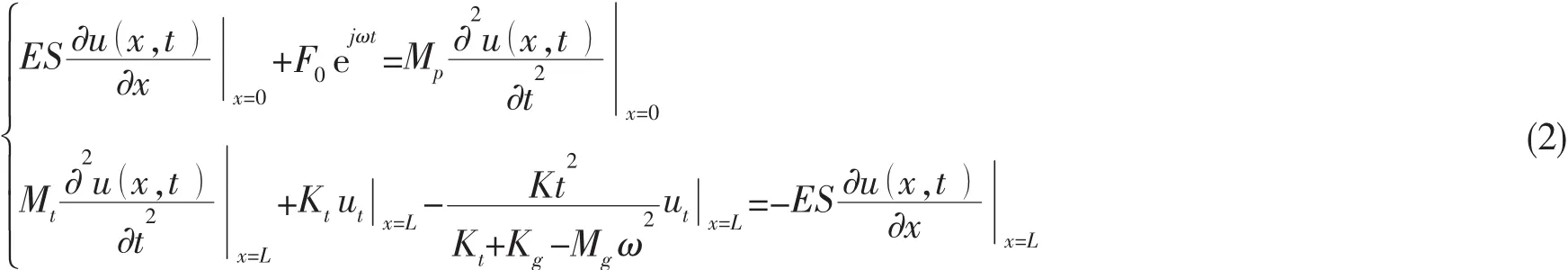
可以看出,图3中(a)、(b)两模型对应的边界条件是相同的。运用(1)式代入两端边界条件,螺旋桨脉动力作用位置x0=0,化简可得:
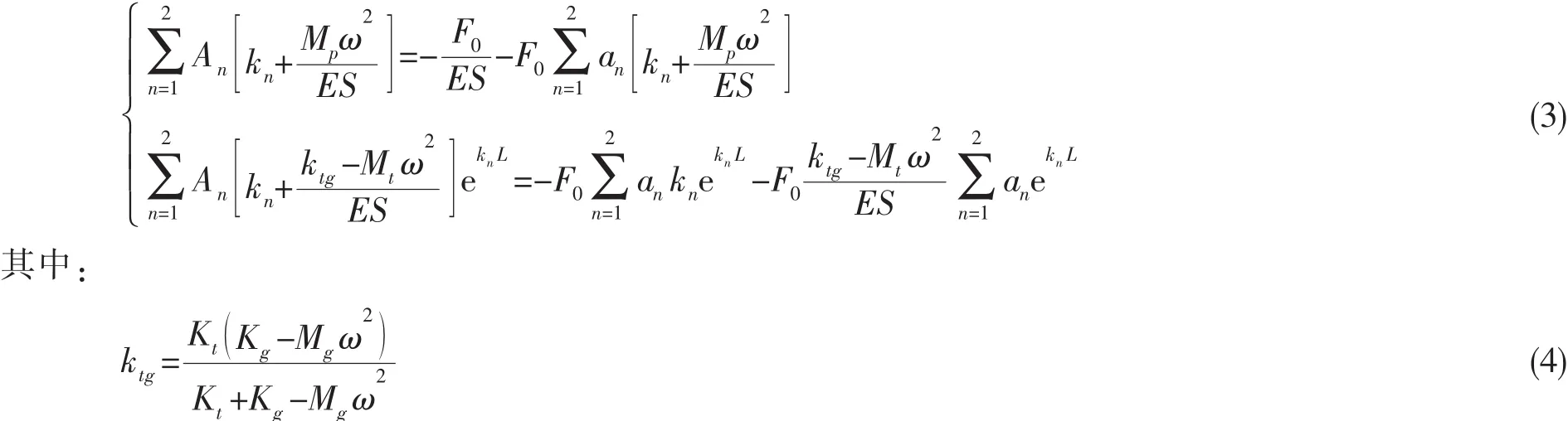
ktg具有刚度的量纲,定义为推力轴承与支承子系统的耦合纵向刚度,(3)式中含有两个未知数,对某一固定激励频率可求得波幅系数A1、A2,从而得到轴系上任意一点的纵向振动位移响应,在一定频段内扫频就可以得到轴系上任意一点的纵向振动位移频率响应曲线,其峰值对应的是系统固有频率。
2 轴系纵振动态特性
2.1 轴系纵振动态特性
当激励力F0=0时,(3)式为关于系数A1、A2的齐次方程:
上述方程若有非零解,系数矩阵为0,可得轴系纵振特征频率方程:
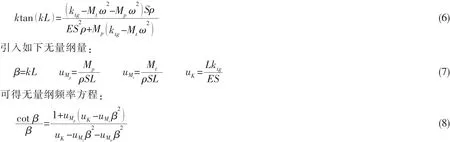
(8)式可借助图解法求得轴系纵振各阶固有频率。引用文献中轴系结构相关参数[7],对推力轴承传统支承条件下,运用图解法求解轴系纵振各阶共振频率。
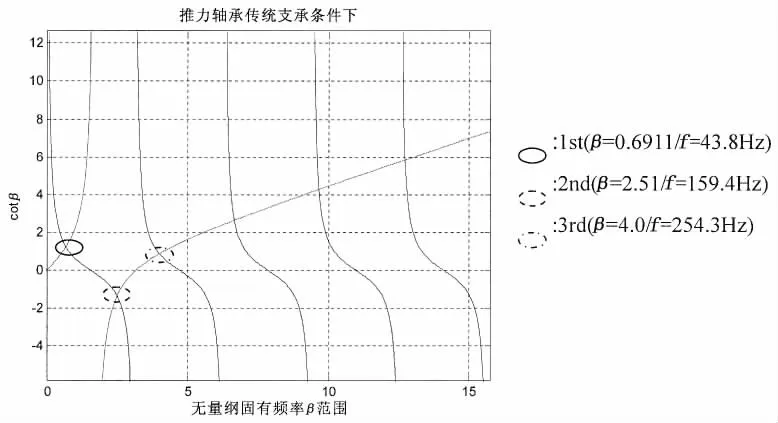
图4 图解法轴系无量纲固有频率Fig.4 The graphic method of shafting dimensionless natural frequencies
图4中两曲线交点即为无量纲固有频率,由于(8)式右端分母含有未知项ω,故轴系纵向振动一阶、二阶无量纲固有频率分布在(8)式右端分母的间断点两侧,即β1<β断<β2。对于低转速船舶,主机常用转速往往能够避开轴系二阶及二阶以上纵振固有频率,故国内外学者多将轴系一阶纵振固有频率作为研究对象,对(8)式左端运用泰勒级数展开,可近似得到轴系一阶纵振无量纲固有频率与各无量纲参数的关系式:
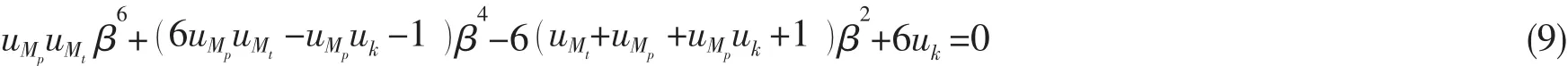
(9)式可用于估算轴系纵振一阶固有频率,计算结果如表1;此外,还可得到轴系一阶无量纲固有频率与各无量纲参数的影响曲线。概括来说,一阶无量纲固有频率β与uMp、uMt是负相关的,与uk是正相关的;各参数影响权重取决于初始值大小,对于一般推进系统,螺旋桨质量及推力轴承刚度对轴系一阶固有频率影响较大。

表1 轴系纵向振动一阶无量纲固有频率计算结果Tab.1 The computation results of the first-order dimensionless natural frequency of longitudinal vibration of shafting
2.2 轴系受迫振动响应
对(3)式进行0-300 Hz扫频,计算中F0=1 N,以log10(u)为纵坐标,可得轴系上各点(x=0,4 m,8 m,13.5 m(轴系全长))的频响曲线。
从图5可以看出,轴系上不同位置处各点在0-300 Hz内的频响曲线有三个波峰,分别在43.1 Hz、159.1 Hz和253.1 Hz处,代表了轴系纵振前三阶固有频率,计算结果与图解法一致(图4所示),曲线波谷代表了不同位置处的反共振频率。此外,代入(3)式轴系前三阶固有频率,可得轴系上各点纵振位移,即轴系前三阶固有振型,在此不再赘述。
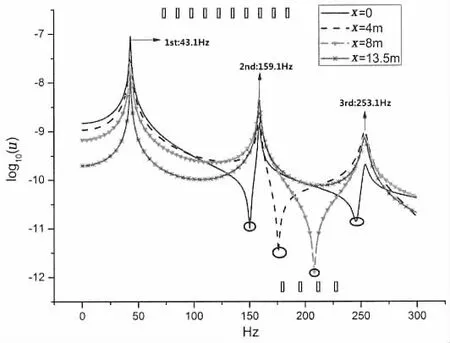
图5 轴系上各点频响曲线Fig.5 The frequency response curves of different locations on shafting
3 算例分析
上一节参考文献[7]中轴系参数,分析推力轴承传统支承条件下轴系纵振动态特性,表明弹性波理论应用在轴系纵振研究合理性。本节结合某型船舶参数,以力传递率作为指标,分别评估推力轴承不同支承形式下轴系纵振减振效果,其轴系初始参数如表2所示。

表2 轴系初始参数Tab.2 The initial parameters of shafting
为保证轴系运行安全性,在选取支承子系统参数时,推力轴承合理的纵向位移是前提。第1章已证明集成隔振系统与RC支承子系统对于推力轴承端的边界条件是一致的,同样设计参数下推力轴承处的纵向位移也一样;暂取支承子系统刚度Kg=2e9N/m,分析现有轴系匹配的支承子系统最优系统参数。
从图6可以看出,该船舶轴系一阶纵振固有频率约在31 Hz,推力轴承弹性支承后,频响曲线中出现代表子系统固有频率的波峰(第一个波峰),原轴系一阶固有频率发生改变;增大子系统固有频率,频率变化量变大(fIVI/RC=40 Hz,fs=44 Hz,Δfs=13 Hz),同时子系统有限刚度使系统总刚度减小,推力轴承处响应被放大,放大数值随子系统固有频率的增加而增加,由于子系统质量的减小,减弱了子系统惯性力对推力轴承位移的约束作用。轴系上各点允许的纵向位移主要由艉轴的密封装置及轴系艏端的联轴器限制,在几毫米的范围数量级,经验表明以推力轴承纵向位移代表轴系各点位移是合理的,图6表明支承子系统刚度数值匹配现有轴系方案,波峰处的瞬时位移可通过增大阻尼衰减。

图6 支承子系统不同固有频率下,推力轴承纵向位移曲线Fig.6 The longitudinal displacement curves of thrust bearing under different natural frequencies of supporting subsystem

图7 推力轴承及支承子系统输入输出示意图Fig.7 The scheme on input&output of thrust bearing and its supporting subsystem
由于集成隔振系统与RC支承子系统分别采用了质量与弹簧串联、并联的方式,其力传递率表达式将不同,在此借用四端参数法对推力轴承及其支承子系统输入输出做定性分析,化简可得推力轴承及其支承子系统的力传递率:

式中:f1为目标频率,即轴系一阶纵振固有频率,f2为支承子系统固有频率;从上式可以看出,集成隔振系统在高频段以24 dB/oct衰减轴系振动,而RC支承子系统以12 dB/oct衰减轴系振动,同时过大的质量将减小力传递率,因此,较集成隔振系统,RC子系统的工作频率较高。现阶段工程上集成隔振系统已达到质量最大数百吨,固有频率低至3-5 Hz,RC子系统设计参数选取范围较大,因此,在子系统刚度数值匹配轴系参数下,分析集成隔振系统与RC子系统最优工作频率。
从图8可以看出,与频响特性一致,力传递曲线出现了代表子系统固有频率的波峰;(a)集成隔振系统:增大系统质量,即减小系统固有频率,对原轴系一阶纵振固有频率几乎无调频作用,但会扩大低频减振带,增大减振效果,fIVI=5 Hz时,7-30 Hz时,减振效果大于20 dB;(b)RC支承子系统:表现动力吸振特性,即fRC处出现反共振,低频段减振频带较窄,减小系统质量会扩大减振频带,fRC=30 Hz时,fs=31 Hz→fs1=20 Hz、fs2=39 Hz,调频效果约为10 Hz。

图8 不同支撑子系统固有频率下,力传递率曲线Fig.8 The force transmissibility curves under different natural frequencies of supporting subsystem
以上对比分析可以看出,对于轴系纵向振动,集成隔振系统在减振频带和减振效果上优于RC支承子系统,即便在声辐射特征丰富的低频段也能够达到减振20 dB的效果;而RC支承子系统表现动力吸振特性,对轴系纵振固有频率的调频作用较集成隔振系统较好。在此,对比最优工作频率下集成隔振系统与RC支承子系统对轴系纵振的衰减效果,同时考虑工程可行的集成隔振系统与RC支承子系统的不同组合情况。
从图9可以清楚地看出,集成隔振系统能够有效衰减轴系纵向振动,7-30 Hz频段,减振效果大于20 dB,48-100 Hz以24 dB/oct衰减轴系振动,但对轴系纵振一阶固有频率无调频作用;RC支承子系统表现动力吸振特性,fRC=30 Hz处出现反共振,调频效果约为10 Hz,48-100 Hz以12 dB/oct衰减轴系振动;同时,基于线性系统叠加原理,集成隔振系统与RC支承子系统串联,能够叠加两者优点,消除原轴系一阶共振峰,实现较大频段内衰减轴系纵振,48-100 Hz以36 dB/oct衰减轴系振动;两RC支承子系统串联有助于扩大调频效果,48-100 Hz以12 dB/oct衰减轴系振动。

图9 不同组合情况下力传递率曲线Fig.9 The curves of force transmissibility under different combination with IVIs and RCs
4 结 论
针对低转速船舶艉部低频振动引发的辐射噪声问题,以轴系纵振作为切入点,运用结构弹性波理论建立了轴系纵振理论模型,详细推导了轴系纵振特征频率方程,重点分析了集成隔振系统与RC支承子系统对轴系纵振的衰减效果,得出如下结论:
(1)结构弹性波理论应用于轴系纵振研究,物理意义明确,计算结果清晰,易于推导完整的轴系纵振特征频率方程解析式;
(2)结合某型船舶参数,在保证轴系纵向变形量的基础上,集成隔振系统在较大频段内能够有效衰减轴系纵向振动,低频段7-30 Hz,减振效果大于20 dB,解决推力轴承低频振动难题,其中增大系统质量有助于扩大低频减振带,增大减振效果;RC支承子系统更多体现动力吸振特性,实现轴系纵振共振转换,调频效果约为10 Hz,低频段减振频带较窄,减小系统质量有助于扩大减振频带;
(3)集成隔振系统与RC子系统串联,能够叠加两者优点,实现调频及减振功能,在较大频段内衰减轴系纵向振动,高频段以36 dB/oct衰减轴系振动;两RC子系统串联有助于扩大调频效果。
[1]Merz S,Kinns R,Kessissoglou N J.Structural and acoustic response of a submarine hull due to propeller forces[J].Journal of Sound and Vibration,2009,325:266-286.
[2]Goodwin A J H.The design of a resonance changer to overcome excessive axial vibration of propeller shafting[J].Institute of Marine Engineers-Transactions,1960,72:37-63.
[3]Dylejkoa P G,Kessissogloua N J,Tsob Y,Norwoodb C J.Optimization of a resonance changer to minimize the vibration transmission in marine vessels[J].Journal of Sound and Vibration,2007,300(1-2):101-116.
[4]何江洋,何 琳,帅长庚,等.船舶动力设备及推力轴承集成隔振系统设计研究[J].舰船科学技术,2013(1):126-131. He Jiangyang,He Lin,Shuai Changgeng,et al.Design research of integrated vibration isolation system for marine power equipment and thrust bearing[J].Ship Science and Technology,2013(1):126-131.(in Chinese)
[5]Mead D J,Yaman Y.The harmonic response of uniform beams on multiple linear supports:a flexural wave analysis[J]. Journal of Sound and Vibration,1990,114(2):465-484.
[6]Mead D J,Yaman Y.The response of infinite periodic beams to point harmonic forces:a flexural wave analysis[J].Journal of Sound and Vibration,1991,144(3):507-530.
[7]张 维,李天匀,赵 耀,等.基于液压阻尼减振器的轴系纵振控制研究[J].中国造船,2012,53(1):18-27. Zhang Wei,Li Tianyun,Zhao Yao,et al.Research on axial vibration control of ship shafting based on hydraulic damping shock absorber[J].Shipbuilding of China,2012,53(1):18-27.
Research on longitudinal vibration isolation of marine shafting under elastic supporting forms of thrust bearing
HE Jiang-yang1,2,HE Lin1,2,XU Wei1,2,LI Zheng-min1,2
(1.Institute of Noise and Vibration,Naval University of Engineering,Wuhan 430033,China; 2.National Key Laboratory on Ship Vibration&Noise,Wuhan 430033,China)
Based on the theory of elastic wave in structure,through the established longitudinal vibration model of the shafting which takes thrust bearing and its supporting system as one boundary condition,the frequency characteristic equation of longitudinal vibration was derived and the first-order natural frequency with Taylor series was estimated.Then combined with a certain ship parameters,the comparative research on the isolation effect of shafting longitudinal vibration between Integrated Vibration Isolator and Resonance Charger was put.The results show that the effect of Integrated Vibration Isolator could be better in large frequency bands,while RC more performance characteristics of DVA;furthermore,on the basis of safety operation of the shafting,larger damping frequency bands could be acquired with more weight of Integrated Vibration Isolator and less of RC.
theory of elastic wave;thrust bearing;elastic support;longitudinal vibration isolation;
P75
:Adoi:10.3969/j.issn.1007-7294.2017.05.012
1007-7294(2017)05-0613-08
2016-11-05
湖北省自然科学基金资助项目(2014CFB223)
何江洋(1987-),男,博士研究生,E-mail:hjywuhan@sina.com;何 琳(1957-),男,教授,博士生导师。

