不同风向角对高架运行磁浮列车气动特性影响分析

黄尊地，周镇斌，陈争卫，常宁，伊严严，陈传仰

（1.五邑大学 轨道交通学院，广东 江门 529020；2.香港理工大学 土木及环境工程系，香港 九龙 999077）

近年来，在绿色低碳背景下，磁悬浮列车具有广阔的应用前景[1-2]. 与轮轨列车不同，磁浮列车是通过磁浮力来推动列车行进. 在横风环境下，高架磁浮列车运行会受到横向冲击载荷，严重时甚至会危及行车安全.

目前，越来越多学者对磁浮列车的气动载荷进行研究. 梁习锋等[3]利用动网格研究了横风环境下平地磁浮列车等速交会的横向气动性能. 毕海权等[4-5]利用数值模拟方法研究了平地磁浮列车在不同车速、风速环境下运行的气动特性. 刘堂红等[6]对不同外形的磁浮列车气动性能进行了研究，结果表明磁浮列车和轮轨列车的气动性能随外形变化的规律基本一致. 丁叁叁等[7]对平地五车编组高速磁浮列车的气动升力性能及气动升力控制进行研究，结果显示气动升力主要集中在头车和尾车，且车体底部与轨道间的间隙决定升力的分布规律. 孟石等[8]对无风及横风环境下的不同轨道间隙的两车编组磁浮列车的气动特性进行了研究，在无风环境下随着轨道间隙增加，头车升力减小、尾车升力增加；在横风环境下随轨道间隙增加，头车和尾车的升力呈减小趋势. Zhou 等[9]采用数值模拟方法研究了新型高速磁浮列车的绕流特性，揭示了磁浮列车引起的涡流特性. Tan 等[10]对不同编组（两车、四车和八车编组）磁浮列车的流场结构进行数值模拟分析，结果显示随编组长度增加尾车流动分离的位置提前了. 高锋等[11]采用数值模拟方法对横风环境下中速磁浮列车在单线高架运行气动特性进行分析，结果表明列车受到的气动载荷与风速呈正相关，与车速呈负相关的关系. 但鲜有学者系统性地研究在横风环境下磁浮列车在高架运行的气动特性，因此，本文采用数值计算的方法，对横风作用下高速磁浮列车以不同车速（430 km/h、600 km/h）及风向角（0°、15°、30°、45°、60°、75°、90°）在高架运行的空气动力学特性进行研究，探讨横风作用下列车的气动载荷大小及性能.

1 数值模拟计算

1.1 数值计算模型

本文采用3 车编组的磁浮TR08 列车简化模型，该模型的头、尾车几何外形相同，头、尾车长27.12 m，中间车长25.50 m，总车长L79.74 m ，车宽W3.70 m ，车高H4.00 m. 高架桥面与地面的距离为6.0 m，列车底部与轨道间的间隙为0.1 m.VT为车速，VW为风速，VT与VW之间的夹角β为风向角. 磁浮列车及高架几何模型如图1 所示.本文研究车速TV为430 km/h 和600 km/h. 在数值模拟计算中，当马赫数Ma ＞0.3，即速度大于368 km/h，必须考虑空气的可压缩性[12]. 在夏季或秋季，沿海地区经常遭遇台风天气，其中心风速达到32.7 ～41.4 m/s，考虑到热带气旋边缘的风速小于32.7 m/s. 因此，研究风速WV为30 m/s 及风向角β为0°～90°. 横风环境下，磁浮列车在高架桥上运行时周围的空气流动为湍流流动. 目前，数值模拟方法主要有直接数值模拟（DNS）、大涡模拟（LES）、雷诺应力模型、涡粘性模型（k-ε与k-ω模型）等方法[13-15]. 本文采用标准k-ε双方程模拟列车周围的湍流流动，因其不仅使用最广泛而且节省计算资源和时间[16-17]. 选用SIMPLEC 算法[18]求解速度和压力的耦合方式，采用基于格林高斯的单元法控制梯度变化. 离散对流相、动量方程、k-ε双方程均采用更高精度的QUICK 格式.

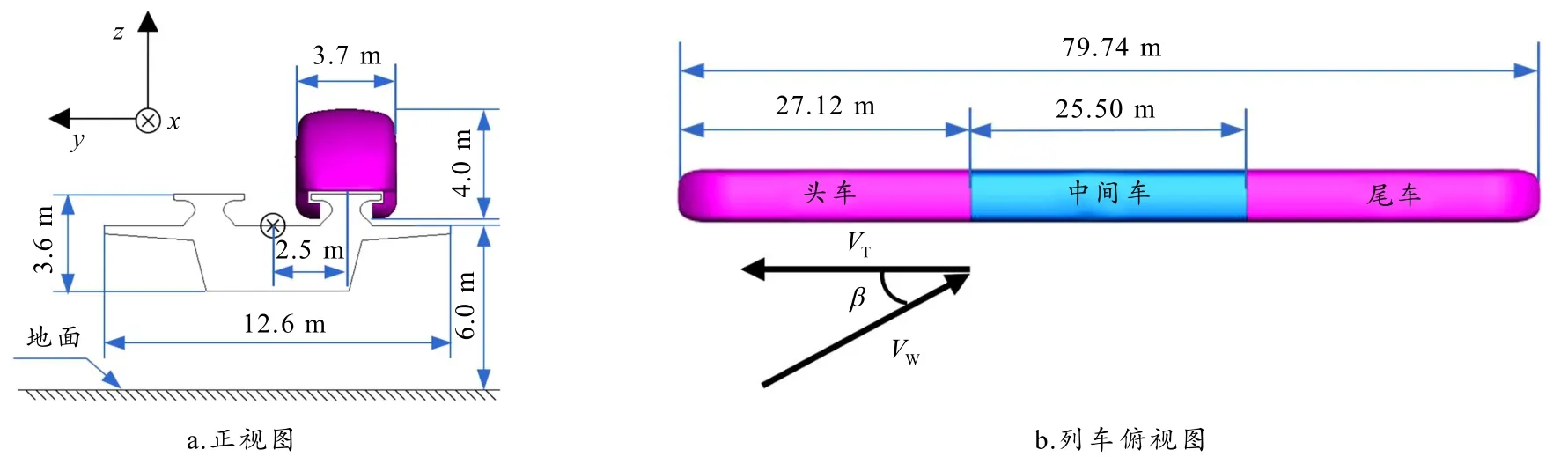
图1 计算几何模型

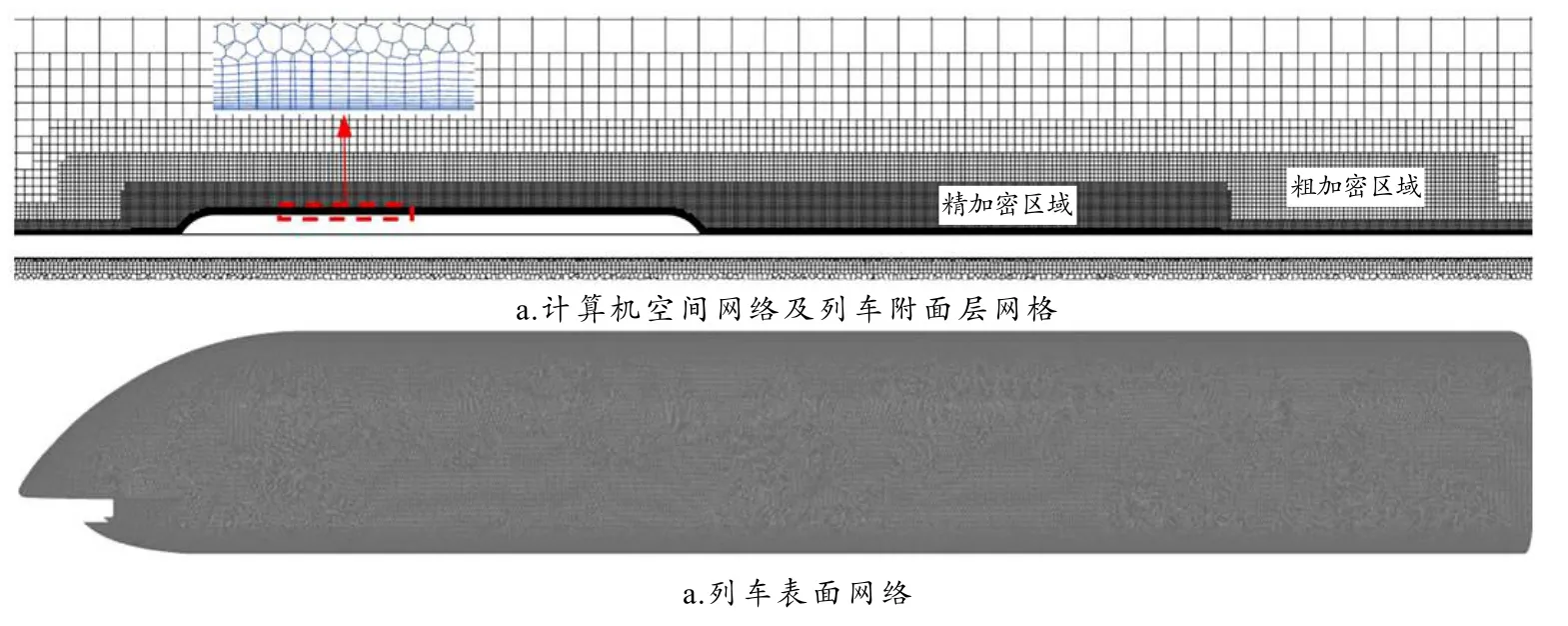
图3 列车表面及空间网格

图4 列车纵向中心线表面压力系数CP 分布图

1.2 计算区域与边界定义

本文采用静止吹风法[8]（列车静止，轨道、高架和地面运动）模拟列车在高架桥运行的外部流场. 该方法已经普遍应用于国内外对列车明线运行时气动性能的研究[18-20].计算区域如图5 所示，列车前方边界ABCD为压力远场，后方边界EFGH 为压力出口，迎风侧边界 BCGF 为压力远场，背风侧ADHE 边界为压力出口. 为了避免回流对数值模拟的影响，列车前端鼻尖点距离前方压力远场20H，列车后端鼻尖点距离后方的压力出口50H；列车纵向中心线距离迎风侧边界压力远场15H. 计算区域的轨道、高架和地面设置为移动壁面，顶部设为对称壁面.

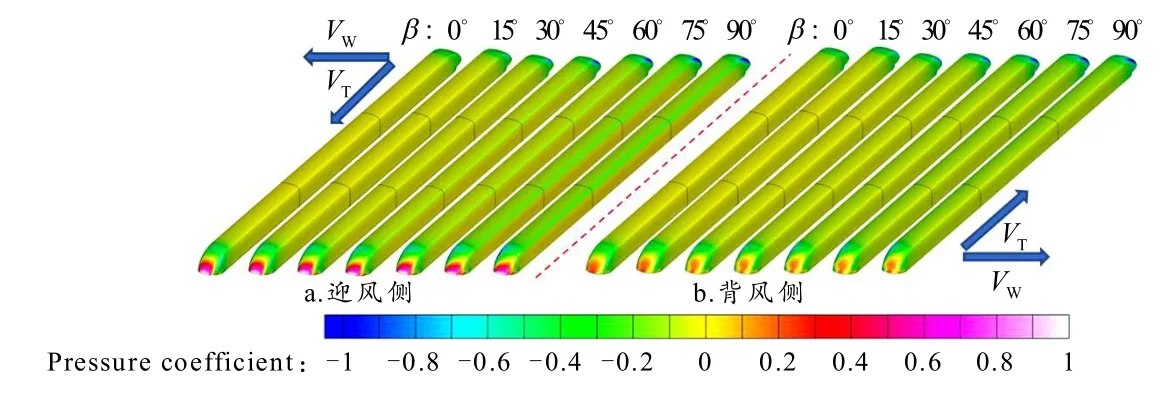
图5 列车表面压力云图

图5 计算区域与边界条件

1.3 计算网格及验证

本文采用CFD 软件Ansys Fluent 进行网格划分和计算，利用马赛克网格Poly-Hexcore[21]划分空间域网格，在列车车体表面设置附面层网格，附面层的纵横比为1 :10，增长比为1.2，共10 层. 为了提高流场结构可视化分辨率，在车体附近区域（背风侧、尾流区域和车底间隙）进行网格加密.

为了验证计算结果与网格划分的相关性，本文对计算区域设置3 套不同尺寸的网格，其中网格数量分别为 13.78 ×106、 29.85 ×106和 57.15 ×106. 通过数值模拟计算得到不同网格密度的列车头、中、尾车及整车侧向力Fs结果，如表1 所示.

表1 不同网格下侧向力 sF 的计算结果

与精密网格计算得出的侧向力sF相比，稀疏网格计算得出头、中、尾车及整车侧向力sF与之偏差分别为2.4%、7.5%、13.1%和0.9%；中等网格计算得出头、中、尾车及整车侧向力sF与之偏差分别为1.3%、2.9%、2.1%、和0.3%. 中等网格计算得出头、中、尾车及整车侧向力sF结果与精密网格相比误差都在2%以内，符合精度误差要求. 综上所述，本文采用中等网格尺寸，列车表面及空间网格如图3 所示.

为了方便对比分析，本文将对压力P进行无量纲参数处理. 压力系数Cp如式（1）所示.

式中，ρ为空气密度，取 1.225 kg/m3；V为车速与风速的合成速度；P0为列车表面压力；P∞为参考压力，取0 Pa.

本文基于中南大学的磁浮列车风洞实验[8,10]进行算法验证. 风洞试验模型测试段的长、宽、高分别为15 m、3 m 和3 m. 风洞实验室的最大风速达到94 m/s，稳定风速20 ～70 m/s. 为了保证数值模拟的准确性，采用与文献中一致的 1 :16 列车模型，轨道间隙为0.01 m. 网格划分及算法见前文.图4 为列车纵向中心线表面压力系数CP分布图.由图4 可知，与风洞试验得到CP相比，通过数值计算得到各测点的压力系数CP的偏差基本在8.2%以内，除了尾车部分测点CP偏差大于 10%之外. 由于尾车尾端受到尾涡影响，导致列车尾部部分测点CP与风洞试验相比偏大. 因此本文的数值模拟方法具有一定的可靠性.

2 列车外部流场分析

2.1 列车表面及周围压力分布

当车速TV为600 km/h、风向角β为0°、15°、30°、45°、60°、75°、90°及WV为30 m/s，列车表面压力云图如图5 所示. 根据伯努利定理可知，流速快则压力小，流速慢则压力大. 由图5 可得，当β为0°时，列车表面压力呈对称分布. 当空气流过头车鼻尖点时会在此处产生驻点. 当β由0°增加到90°时，头车压力系数CP较高区域逐渐向迎风侧偏移；而尾车鼻尖点处CP较高的区域也向车体背风侧偏移，且尾车驻点附近CP逐渐减小. 除此之外，车体迎风侧表面CP逐渐增大，背风侧表面CP逐渐减小，从而导致列车车体两侧的压差逐渐增大.

2.2 列车周围涡量分布

TV为600 km/h、β为0°、90°及WV为30 m/s，列车垂向截面（1.26 mz=）涡量分布图见图6.

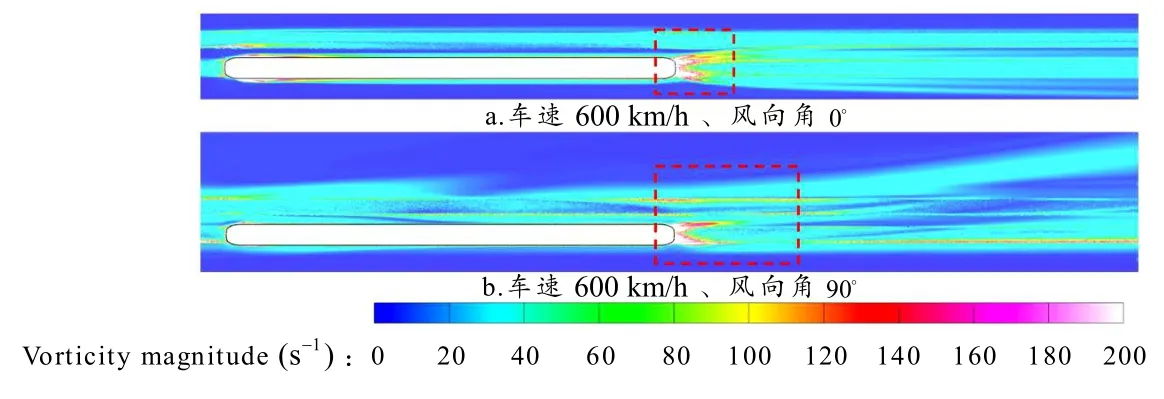
图6 列车垂向截面（z=1.26 m ）涡量分布图

由图6 可知，当TV为600 km/h、β为0°时，列车尾部有两对有对称性的尾涡，且尾涡强度和尺度较小. 当β为90°时，列车尾部只有一对非对称性的尾涡，其强度和尺度都较大. 漩涡在尾车出现流动分离后在横风的作用下，尾涡更复杂且沿着背风侧偏移. 与β为0°相比，β为90°时尾涡的强度、尺度及作用范围更大、更广.

3 列车气动载荷分析

3.1 侧向力

高速列车在横风环境下行驶将受到较大的侧向力[22]，即横风环境导致列车运行的横向稳定性恶化. 当VW为30 m/s，不同车速VT列车受到的侧向力Fs如图7 所示.VT为430 km/h 和600 km/h 时，头、中、尾车Fs的变化规律基本一致. 头车、中间车Fs随β增大而增大；尾车|Fs|随β增大呈现先增加后减小的趋势. 当β相同时，VT对头车Fs影响最大；当VW、β相同时，头车的Fs最大，尾车次之，中间车最小，即头车的横向稳定性最差.

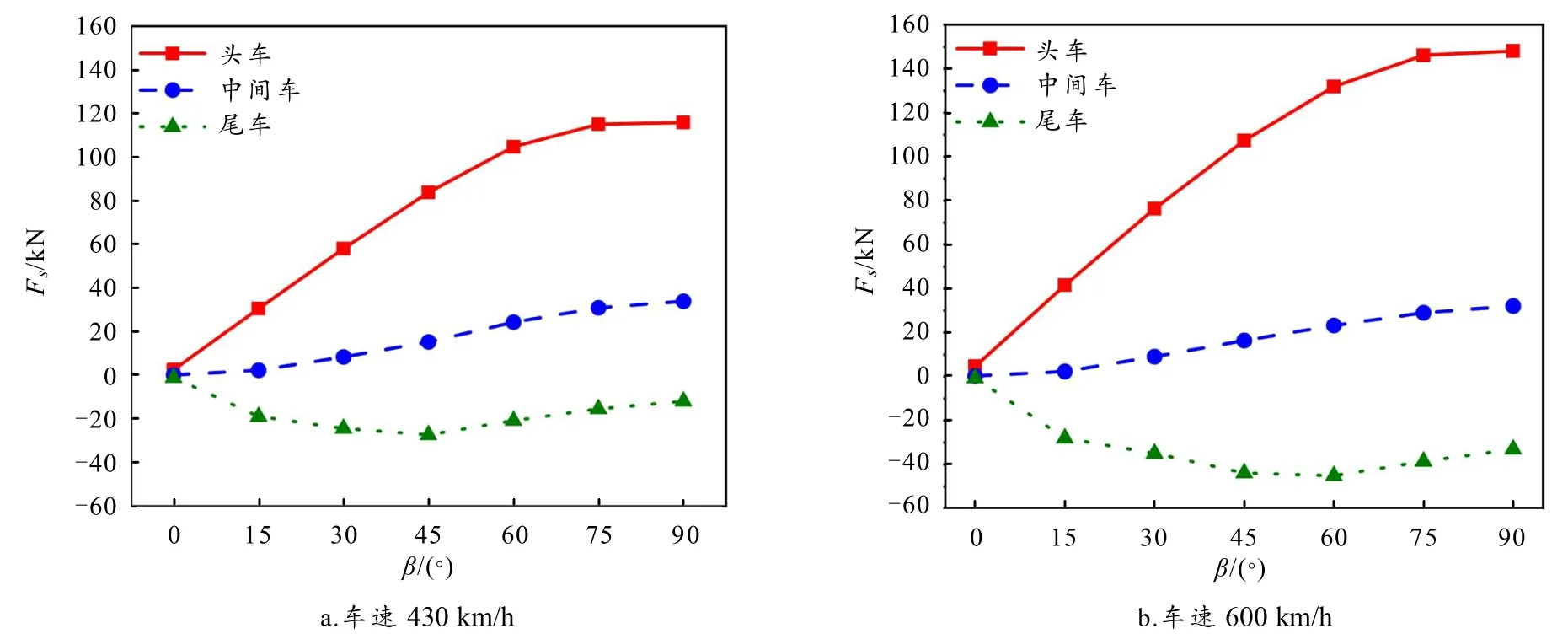
图7 不同车速侧向力图

3.2 升力

高速列车在横风环境下行驶，列车的垂向稳定性也会受到影响. 当WV为30 m/s，不同车速TV列车受到的侧向力lF如图8 所示. 当TV相同时，随着β增大，列车头、中、尾车lF曲线规律与sF曲线规律相似，头车、中间车lF也随之增大，尾车lF则先增大后减小；当β相同时，TV对尾车lF影响最大. 当WV、β相同时，尾车的lF最大，头车次之，中间车最小，即尾车的垂向稳定性最差.

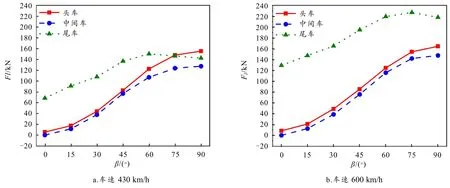
图8 不同车速升力图

3.3 倾覆力矩

当VW为30 m/s，不同车速VT列车受到的侧向力Mx如图9 所示.VT为430 km/h 及600 km/h，头、中、尾车|Mx|的变化规律基本一致. 当VT为430 km/h 和600 km/h 时，头、中、尾车|Mx|的变化规律一致. 随β增大，头车|Mx|先增大后减小；中间车、尾车|Mx|呈现增大趋势. 列车的倾覆力矩受到侧向力及升力共同影响，导致列车头车及尾车|Mx|较大.

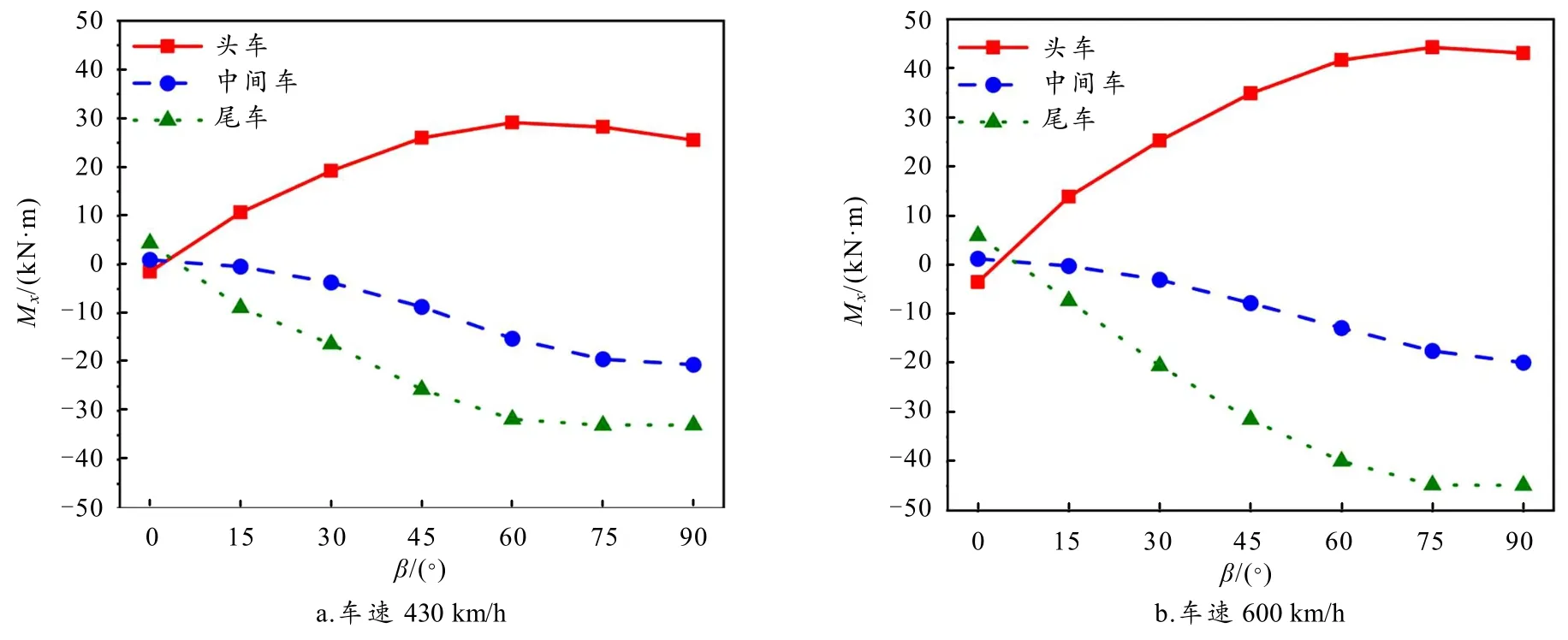
图9 不同车速倾覆力矩图

4 结论

本文利用标准k-ε双方程对不同风向角及不同车速磁浮列车在高架运行的气动特性进行数值计算，并对列车表面压力、列车周围流场结构及气动力进行分析. 得出如下结论：1）风向角越大，列车车体两侧的压差越大；2）当风向角为0°时，尾涡具有明显的对称性，且尾涡强度及尺度都较小；当风向角为90°时，列车尾涡呈现明显的非对称性，尾涡的强度、尺度及作用范围更广，对周围铁路环境有一定影响；3）综合气动力分析，当车速一定时，列车气动载荷基本随风向角增大而增大，头车侧向力最大，尾车升力最大. 气动力的最不利风向角范围集中在60°～90°之间.

本文的研究结果可为横风环境下高架运行高速磁浮列车的运行安全行提供理论依据，但未对不同风速、编组、磁浮间隙等进行全面分析，后续将开展深入研究.