基于GA-BP神经网络的颗粒阻尼器减振特性预测

游佳凝，高 玲，王 庆

(1.中国农业大学信息与电气工程学院，北京 100091；2.贵州大学公共管理学院，贵州 贵阳 550025)

颗粒阻尼是一种通过粒子碰撞能量耗散来实现有效减振的技术．由于其耗能效率高，减振效果好，结构紧凑简单，在实际生活中常用于机械减振和降噪，近年来被广泛运用到各个行业领域．近几年，关于颗粒阻尼的研究一直是热门问题．其中，在颗粒阻尼器的应用领域中，阻尼特性对阻尼起着决定性的作用，成为重要的研究方向之一．

许多国内外专家学者对此进行了实践和研究．国内，胡溧等[1]利用回归设计的方法，进行二次回归正交组合试验，建立颗粒阻尼减振特性的非线性回归模型.将该模型应用于预测，并通过试验验证该回归模型的正确性．鲁正等[2]系统阐述颗粒阻尼理论分析、数值模拟及试验研究发展，重点研究了多自由度结构附加颗粒阻尼器离散元模拟方法．在悬臂梁的颗粒阻尼方面，夏兆旺等[3]以填充颗粒的悬臂梁为研究对象，研究了结构阻尼随颗粒各参数呈非线性变化的特性，同时还系统研究了颗粒参数和结构参数的变化对结构减振效果的影响规律．杜妍辰等[4]分别对在传统单体碰撞阻尼和带颗粒减振剂碰撞阻尼作用下悬臂梁减振效果进行试验研究，发现以微细颗粒塑性变形消耗振动能量的带颗粒减振剂碰撞阻尼具有优秀的减振效果，远远超过传统单体碰撞阻尼器．在垂直简谐激励条件下，周宏伟等[5]通过稳态功率输入法对颗粒阻尼纵向耦合结构系统的动态特性进行了研究和分析，实验结果表明，在简谐激励作用下由颗粒体引起的周期脉冲力对系统的损耗功率并不产生影响，损耗功率只与激励频率有关．在国际上，Zheng等[6]对带有调谐质量阻尼器和颗粒阻尼器的结构进行了对比研究，发现颗粒阻尼器可以显著降低主体结构与阻尼器本身之间的相对位移．基于改进的对称-偏差耦合应力理论，Dehrouyeh等[7]提出了函数梯度粘弹性阻尼夹芯微梁的尺寸相关数学公式，新建立的模型包含5个材料长度尺度参数来解释夹层微梁的尺寸相关阻尼特性．然而现有的研究主要集中在将颗粒阻尼与实际应用相结合，实现振动阻尼，而对颗粒阻尼器本身的研究还比较缺乏．

目前颗粒阻尼器领域的研究大多是基于对某些特性参数和外界影响参数的分析，而不是对颗粒阻尼器本身特性的综合分析和考察．李来强等[8]曾提出了BP神经网络的改进 LM(levenberg marquardt)算法原理对颗粒碰撞振动系统的阻尼进行了训练和仿真并将此改进算法与传统算法进行比较，发现神经网络训练的模型在稳定性、效率和准确度上均优于传统模型，但由于大型复杂网络时对计算机的性能要求比较高，当权值过多时LM算法并不适用，该模型也没有针对颗粒阻尼器的性能参数，无法很好地对颗粒阻尼减振特性进行预测．

针对上述问题，本文提出将遗传算法和神经网络算法相结合，然后应用于颗粒阻尼特性预测模型．该算法选择ReLU激活函数来研究数据特征在局部范围内的突然变化问题，并使用遗传算法代替反向传播算法计算神经网络权值．本文的贡献如下：

(1)研究了共振频率、颗粒材料、颗粒直径和填充率等性能参数对阻尼效应的影响，并通过神经网络模型预测了颗粒阻尼器的阻尼效应，预测结果能够对颗粒阻尼器的参数选择提供参考；

(2)设计悬臂梁阻尼检测实验，利用悬臂梁、振动器、扫频信号发生器、功率放大器和CA-YD-1181压电式传感器进行测试，基于真实实验结果构建数据集，用于模型训练和结果检测；

(3)利用适应性函数指导权值优化方向，采用遗传算法代替反向传播算法，不需要先利用反向传播算法计算模型导数，再利用梯度下降方法进行最优权值求解，进一步简化了求解算法框架，同时由于其初始种群涵盖范围较广，更不容易陷入局部最优解，提高了收敛速度以及模型预测精度.

1 相关工作

1.1 阻尼技术的应用

柔性臂由于其适应性和交互安全性，近年来受到了研究人员的广泛关注．Zurawski等[9]提出了一种新型调谐粒子冲击阻尼器(TPID)，通过快速调节容器体积达到改变振动系统动态特性的目的．Yang等[10]通过3个薄的气动人工肌肉和一个充满离散粒子的室实现了变刚度减振效果．Bhudolia等[11]通过添加核壳聚合物(C/SH)颗粒显著改善其阻尼和动态力学性能，该方法利用了微波固化具有固化时间短、能耗低等优点．Foong等[12]进行的研究表明，机械阻尼变化对悬臂梁型电磁谐振器特性的建模具有重要影响，而根据共振处的最大临界阻尼应力定义材料阻尼的方法，将使计算过程更简单，计算结果更准确．Zhang等[13]采用自由层粘弹性阻尼材料处理压制了轴向柱塞泵最主要的离散频音，噪声和振动明显降低．为了减少航空航天机械系统中的结构振动，Pan等[14]提出了一种由圆柱形永磁体、两块环形铜板、轴向传动轴和电磁屏蔽组成的涡流阻尼器新结构．

上述研究主要集中在将颗粒阻尼与实际应用相结合，实现振动阻尼，而对颗粒阻尼器本身的研究还比较缺乏．为了更有针对性地调整颗粒阻尼器的参数，提高其阻尼减冲效果，需要研究其设计参数与实际阻尼效果之间的映射模型．

1.2 颗粒阻尼器相关工作

近年来，许多学者基于多种参数对颗粒阻尼的影响进行了相关研究，建立了与设计参数和阻尼效应相关的各种模型．在颗粒阻尼器参数控制方面，Meyer等[15]将离散单元模型与简化有限元模型相结合，在较宽的频率范围内进行多特征模态分析，实验结果表明，系统的频率响应与模态参数具有良好的一致性．基于阀控阻尼的结构特性，Xie[16]建立了阀控阻尼可调阻尼器阻尼特性的数学模型，设计了压缩行程和恢复行程阻尼特性实验，分析了不同激励速度下不同关键参数的阻尼贡献，为阻尼器的设计和优化提供了指导．Wang等[17]利用动态力学分析(DMA)表征数据和粘弹性阻尼材料的动态性能实验研究了结构阻尼的动态性能，分析总结了阻尼材料的性能随温度和频率的函数关系．为了对颗粒阻尼器(pd)的宽带特性进行分类，Schonle[18]寻找了一种量化pd宽带阻尼特性的方法，发现pd在较宽的频率范围内提供了较高的阻尼，并通过适当的pd性能指标量化了宽带阻尼特性．Yan[19]发现粒子与空腔之间的碰撞恢复系数参数、粒子与空腔之间的滚动阻力系数以及粒子半径能够影响pd的阻尼机制和性能，结果表明颗粒阻尼是碰撞和摩擦阻尼机制的混合物．

在颗粒阻尼器的应用领域中，阻尼特性对阻尼起着决定性的作用，有许多学者进行了相关研究．Du等人[20]开发了数值模型来捕捉细颗粒冲击阻尼器所涉及的复杂物理现象，研究表明，在所有情况下，细颗粒冲击阻尼器(FPIDs)的阻尼性能都优于SMIDs (single mass impact dampers)，并且存在最优的参数组合以实现最大的阻尼能力和最小的系统响应．基于粒子动力学，Fowler等[21]开发了一种利用表征颗粒阻尼数据预测结构系统阻尼的分析方法，并验证了阻尼效应在复杂粒子流中复杂碰撞上的作用．为了探究颗粒阻尼器的最优阻尼机理，Kai等[22]开展了一项悬臂系统实验研究，研究了颗粒阻尼器的最优阻尼性能与颗粒在颗粒阻尼器中的运动模式之间的关系，发现最佳阻尼性能主要是由粒子在莱顿弗罗斯特状态下的阻尼耗散特性引起的．

1.3 阻尼特性预测模型相关工作

在颗粒阻尼器阻尼应用领域，学者多采用硬件和软件相结合的方法分析其阻尼特性，更多关注所提出的数值模型和硬件优化．Fiore等[23]探讨了结构阻尼不确定性对阻尼折现因子的影响．Sarikaya等[24]研究了聚合物纳米复合材料阻尼特性的特殊效应，这些都没有基于振动阻尼特性各种参数的预测模型．

如今，神经网络预测已广泛应用于科学研究的各个领域，BP神经网络、RBF神经网络等常用来对各类数据进行模拟和预测，其中GA-BP算法被广泛应用于各种数据预测中．Wang[25]使用集成了经验模态分解(EEMD)的风速信号作为GA-BP神经网络模型的输入数据，对单个信号的预测数据进行聚合，得到最终的预测风速数据．对于短期燃气负荷预测，Yu[26]利用优化遗传算法的全局搜索能力确定BP神经网络的初始权值和阈值，还加入了cat混沌映射以避免陷入局部极小值，并增强了遗传算法的能力．Sun[27]使用遗传算法优化的BP神经网络预测碳价格，在湖北市场的实证分析中，该模型优于其他比较模型，在北京和上海碳市场互补的情况下，该模型也表现最佳．

2 神经网络拟合预测数据方法设计

2.1 基于数据特征的BP神经网络模型

BP神经网络是目前应用较为广泛的神经网络之一，基本的学习规则是使用梯度下降法通过反向传播不断调整网络权值和偏差值，使网络损失函数的值最小．前馈神经网络是通过不断调整网络中的权重和偏差来训练的．图1是一个具有两个隐含层的前馈神经网络架构．其中x1、x2、x3，…，xm为输入层神经元，f(z11)、f(z12)，…，f(z1s)、f(z21)、f(z22)，…，f(z2s)为隐藏层神经元，f(z31)、f(z32)，…，f(z3s)为输出层神经元．zij表示神经元上层的输入，定义yij=f(zij)，表示神经元的输出值．

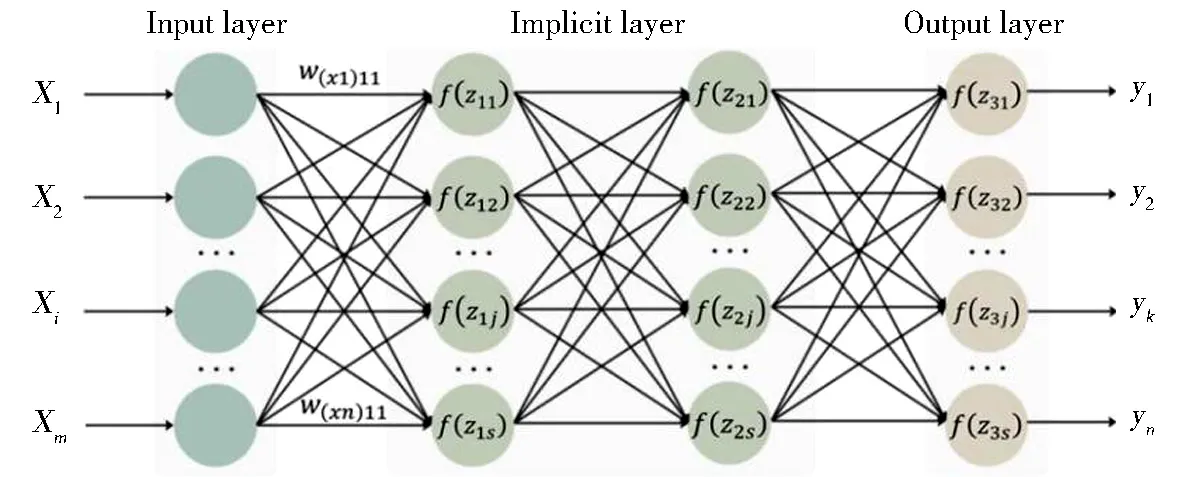
图1 前馈神经网络架构Fig.1 Feedforward neural network architecture

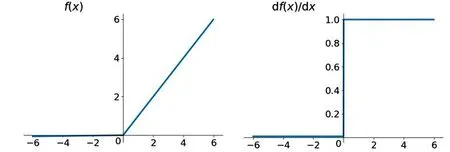
图2 ReLU函数特征曲线Fig.2 ReLU function characteristic curve

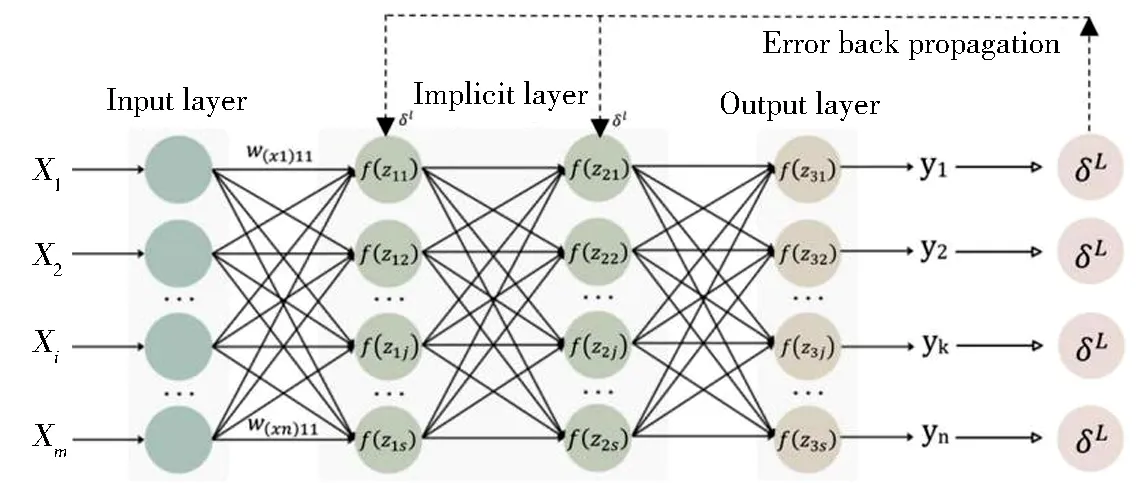
图3 BP神经网络反向传播结构Fig.3 BP neural network back propagation structure

选择不同的网络隐层数和不同的非线性激活函数会对学习结果产生不同的影响，其中激活函数直接关系到BP神经网络的最终输出，影响到非线性误差函数的收敛能力．在梯度消失概率较高的深度神经网络中，为了防止梯度向后转移导致梯度爆炸和梯度消失，Eckle[28]引入了由ReLU函数激活的深度神经网络．他的拟合过程适合于数据集，于是引入ReLU函数来解决梯度消失问题，ReLU函数如下所示：

ReLU=max(0，x)，

(1)

其特性曲线如图2所示，可以看到，在x>0的时候，函数的导数直接就是1，故不存在梯度衰减问题．ReLU函数缓解能够缓解梯度消失的问题，但也可以看到，在x<0的时候，函数的导数直接为0，处于硬饱和状态，一旦输入落这个区域，神经元便不会更新权重，导致神经元死亡．但是，由于阻尼数据均为正数且不具有线性规律，在控制单一变量的情况下，数据变化幅度小且密集，ReLU函数适合为激活函数应用于阻尼特性领域的研究．

2.2 基于GA-BP神经网络模型

2.2.1 反向传播算法

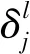
(2)

其中，zl为该神经元的加权输入，δl为向量化表示一层上面所有神经元的误差．

2.2.2 遗传优化算法

由于反向遗传算法形式较为复杂且因只有一个初始值而容易陷入局部最优解．为了克服这个问题，在本文中，引入遗传算法代替反向传播算法进行权值求解．相比于反向传播算法，遗传算法只要计算前馈网络所获得的预测值，并利用适应度函数指导进化方向，不需要进行反向传播以及梯度优化，改进了反向传播算法中反向反馈过程，通过种群的迭代对权值和阈值进行调整和优化，能够有效避免陷入局部最优解的问题，找到全局最优解．

遗传算法优化的BP神经网络算法对算子的基本操作如图4所示，分为遗传算法和BP神经网络算法相互融合的两部分，绿色流程框代表遗传算法相关步骤，蓝色流程框代表BP神经网络训练相关步骤，遗传优化算法的主要步骤如下：

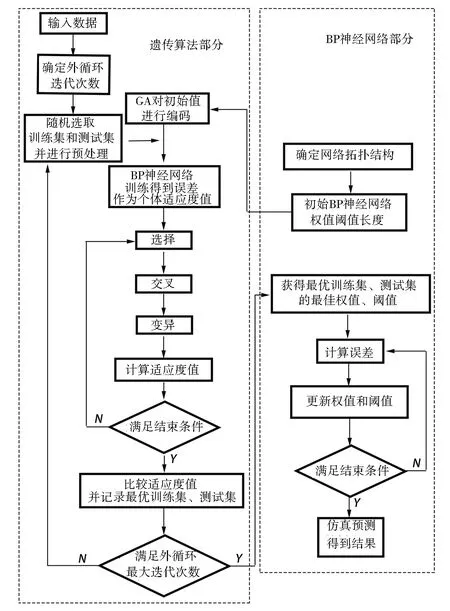
图4 遗传算法优化的BP神经网络流程Fig.4 Flow chart of BP neural network optimized by genetic algorithm

(1)随机产生一个种群，作为问题的初代解，以确保个体基因的多样性；

(2)运用二进制编码方案对种群中的每个个体进行编码，二进制编码长度等于隐含层节点数，并判断权值和阈值是否越界；

(3)以MSE均方误差的值作为个体的适应度值，计算出种群中每个个体的适应度；

(4)采用轮盘赌法，根据适应度的高低选择存活的个体作为父体和母体进行繁衍；

(5)对被选出的父体与母体进行遗传操作，并采用交叉、变异等算子产生出子代，在较大程度保留优秀基因的基础上，变异增加了基因的多样性，从而提高找到最优解的概率；

(6)根据判断标准决定是否继续执行算法，找出所有子代中适应度最低的个体作为解返回并作为最优的BP神经网络初始权值，判断准则为设定的解的阈值、指定的迭代次数．

在上述基本操作的基础上，先在实验数据分训练集和测试集时，进行了二次优化，在外层嵌套了一层循环，迭代出拟合效果最好的训练集和测试集并记录，以此获得最优模型．为防止过拟合现象，在求适应度函数时，本文引入L1正则化概念，加入刻画模型复杂度的指标．L1正则化如下：

R(w)=‖w‖1+∑iwi，

(3)

即假设用于遗传算法选择迭代的适应度函数为J(θ)，在优化时不直接优化J(θ)，而是优化J(θ)+λR(w)，其中R(w)刻画的是模型的复杂度，而λ表示模型复杂损失在总损失中的比例．其中θ表示的是一个神经网络中所有的参数，包括变身的权重w和偏置项b．

在加入了L1正则化项这个与模型有关的参数前，模型倾向于最小化损失函数，极有可能发生过拟合的现象，在引入R(w)后，倘若模型过于复杂，则该项的惩罚值也更大，以此来抑制模型的过度复杂化．

3 实验与算法验证

3.1 悬臂梁减振实验

Gagnon[29]在保持粒子总质量恒定的情况下，使用4个质量几乎相同的不同腔体改变粒子数量，并利用峰值加速度计算阻尼响应、阻尼系数和有效质量变化．Meyer[30]选择了一个由两根柔性电缆支撑的柔性梁组成的实验台，从中可以假定自由边界条件．本节主要研究了结构参数和颗粒参数对颗粒阻尼器阻尼性能的影响，测试内容包括：系统振动频率(155.2、190.7、250.2 Hz)；颗粒类型及直径，其中镀镍铁(1、1.5、2、4 mm)、不锈钢(1.5、2、3、6、9 mm)、钨(2、3、4 mm)、铜(3 mm)；金属箱与悬臂梁固定端距离(20 cm)；金属箱填充率(0%、25%、40%、50%、60%、75%、90%、100%)．

图5 实验测试系统及实验装置Fig.5 Experimental testing system and setup

根据实验装置与本文实验的共性和个性，设计了如图5所示的实验装置，给悬臂梁一定的初始位移，引起金属盒内颗粒的摩擦和碰撞．用于实验的悬臂梁的尺寸为长550 mm、宽25 mm、厚4 mm．将装满颗粒的金属盒密封，然后用强胶粘剂粘在距离振动点位移300 mm位置的悬臂梁上．加速度传感器为CA-YD-1181压电传感器(图5(c))，灵敏度为4 Pc/N，测量范围为0～2000 N．实验采用SA-SG030扫频信号发生器和SA-PA010功率放大器作为振动源(图5(b))，实验装置一阶本征频率为155.2 Hz，二阶本征频率为190.7 Hz，三阶本征频率为250.2 Hz．

3.2 实验数据

部分实验数据如表1所示．

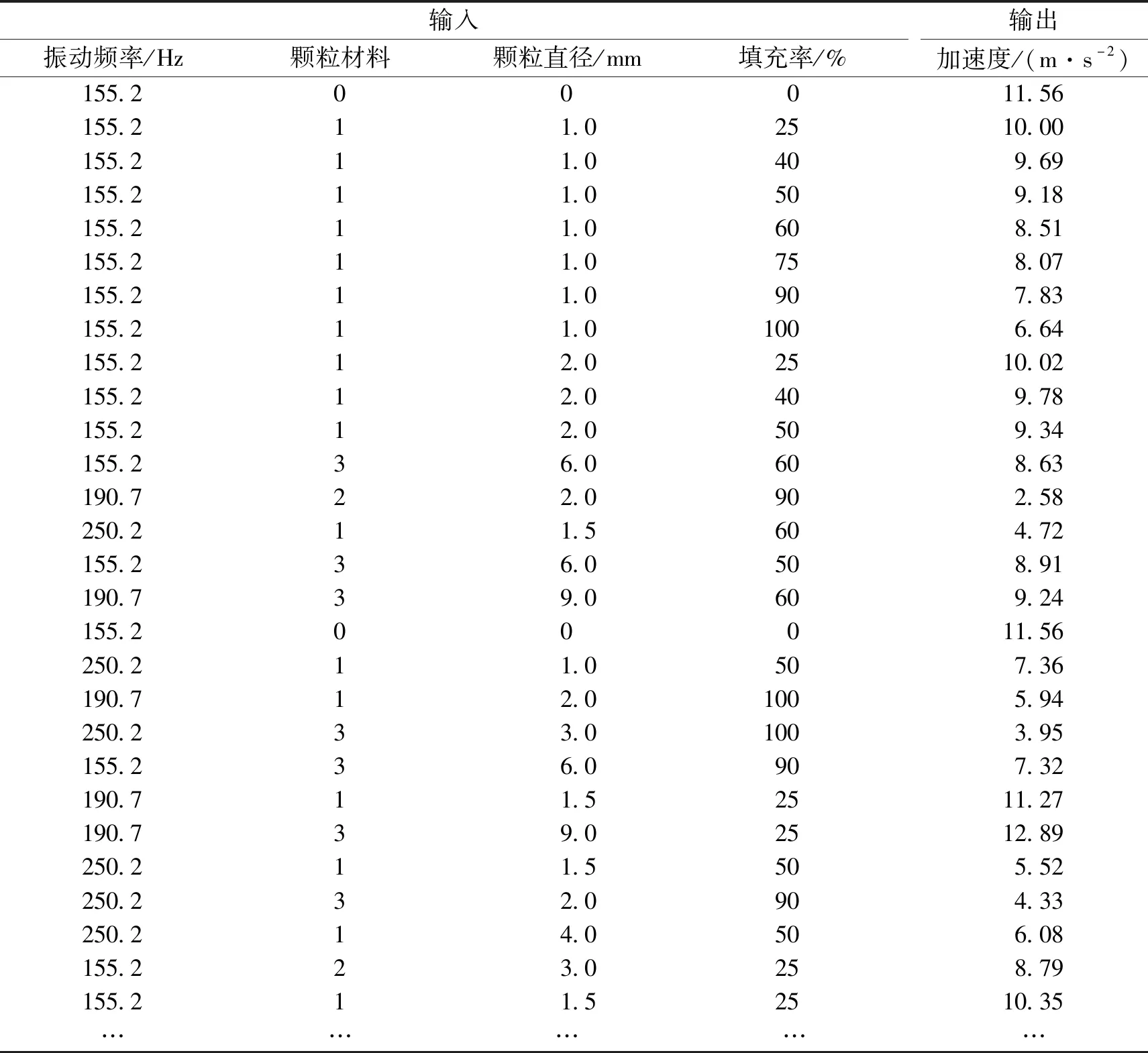
表1 部分实验数据Tab.1 Experimental data

3.3 算法结果分析

本文根据上述算法进行模型建立，利用遗传算法优化的BP神经网络算法拟合不同参数下阻尼减振效果数据集，建立阻尼减振效果影响因素预测模型，在基于算法的基础上，在外层嵌套一层循环以迭代出拟合效果最好的训练集和测试集，每次大循环时打乱数据集，选取前50组数据作为预测集，后226组数据作为训练集，并记录拟合效果最佳的训练集和测试集其结果如图6所示．在遗传算法计算适应度函数时加入正则化项，防止发生过拟合现象，同时对BP神经网络不同激活函数的选择也进行了筛选，并对比ReLU函数作为激活函数的迭代收敛图和sigmoid函数作为激活函数的迭代收敛图，如图7所示．由图7可知，在外循环时对数据集进行二次优化，选择较优的训练集和测试集，获得了更好的拟合效果，提高了遗传算法优化的神经网络的预测精度．以ReLU函数作为激活函数训练的神经网络(图7(a))收敛迭代次数明显优于运用sigmoid函数作为激活函数训练的神经网络(图7(b))，且ReLU具有更高的运算效率，故本文选择ReLU函数作为激活函数构造神经元模型．

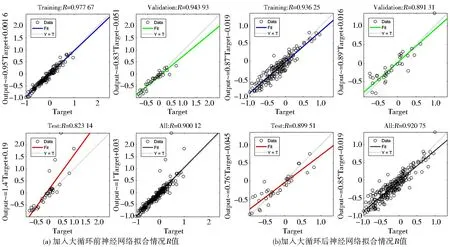
图6 加入大循环迭代前后神经网络的拟合情况R值Fig.6 R-value of the neural network fitting before and after adding large loop iterations

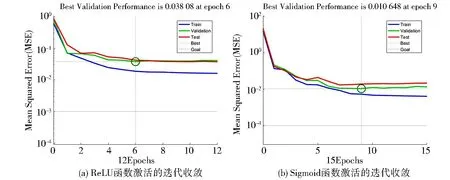
图7 ReLU函数和sigmoid函数激活时迭代收敛图对比Fig.7 Comparison of iterative convergence plots for ReLU function and sigmoid function activation

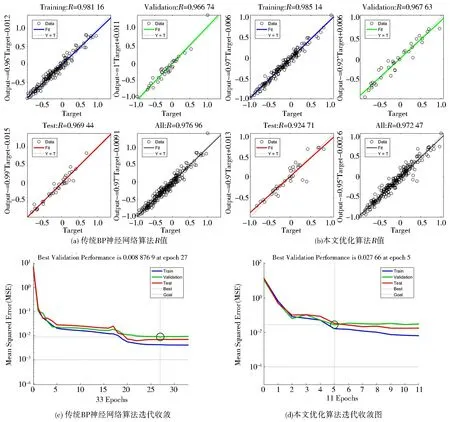
图8 传统BP神经网络与模型算法对比Fig.8 Comparison of traditional BP neural network algorithm and the optimized algorithm proposed

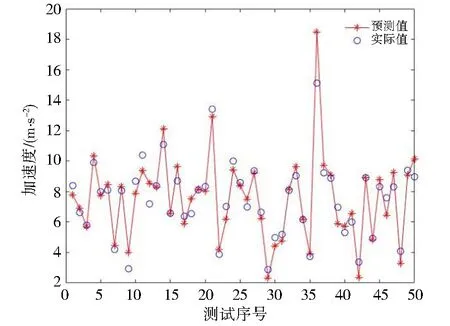
图9 算法拟合结果Fig.9 Algorithm fitting results

为了突出本算法在加快迭代速度和拟合效果方面的优点，与传统BP神经网络算法做对比，保证激活函数、网络层数和结点个数的情况下，对比结果如图8所示．实验发现，提出的优化算法在达到同样均方差，甚至于更低均方差的情况下，迭代到第10-15步基本收敛，收敛速度明显高于传统BP神经网络，且拟合的R值相比于传统BP神经网络有一定程度的优化．最终拟合且遗传算法优化的BP神经网络对于测试集的预测结果如图9所示，可知本文提出的算法和实验所得数据集训练的神经网络对于测试集的拟合效果良好，能够通过不同参数的变化对颗粒阻尼器减振效果进行精准预测，得到各个参数下准确的振动加速度值，以此可对颗粒阻尼器的性能进行可视化评估．

4 总结

本文主要研究了共振频率、颗粒材料、颗粒直径和填充率4个因素对颗粒阻尼器减振效果的影响．根据颗粒阻尼器减振数据局部骤变的数据特征，提出了遗传算法结合神经网络的减振效果预测模型．利用遗传算法代替了反向传播算法，有效解决了计算了神经网络权值的复杂性．同时引入ReLU激活函数进行神经网络模型建模，有效克服了梯度下降问题．所提算法相比于已有的颗粒阻尼器减振效果预测模型，明显提高了数据细节特征的拟合效果．通过独立收集实验数据、创建数据集，使结果具有更实际的参考价值．