多链竞争视角下供应链内部协调定价研究

王 奎,梅亚丽,高太光,2,3,刘 丹,刘春丽

(1.黑龙江科技大学 管理学院,黑龙江 哈尔滨 150022;2.哈尔滨工业大学 管理学院,黑龙江 哈尔滨 150001;3.黑龙江省产权交易集团,黑龙江 哈尔滨 150090)

《第十四个五年规划和2035年远景目标纲要》明确指出,要提升产业链供应链现代化水平,锻造产业链供应链长板,补齐产业链供应链短板,而供应链企业间协调对于产业链供应链优化升级至关重要。供应链内部成员往往以自身利益最大化为目标,与上下游企业间也会存在利益分配、成本分担等问题,如小米手机的线下直营店与线上零售商竞争关系较为紧张,如何合理协调供应链内部各节点间利益冲突,进而实现供应链整体收益最大化目标亟待解决。此外,面对愈加激烈、动态复杂的市场竞争环境,企业依赖自身力量可能难以应对,过去企业间单打独斗的竞争模式逐步被取代,转换为供应链与供应链之间的竞争,如当今电商巨头淘宝和京东、家电行业的苏宁和国美等均属于以核心企业为代表的供应链间竞争。因此,研究供应链间竞争背景下内部成员协调定价,对在满足成员收益合理分配前提下如何实现供应链整体收益最大具有重要意义。

一、文献综述

国内外部分学者从企业行为因素考虑供应链成员间协调:Zhang和Ma[1]基于零售商公平关切行为下的两种定价策略构建Stackelberg和Nash博弈模型,发现价格的快速变动对供应链上制造商不利、对零售商有利,但过度公平关切行为偏好可能导致零售商收益降低;汪峻萍和汪亚[2]在供应链定价决策模型中引入零售商公平偏好行为,研究供应链收益不公平分配对零售商产生的影响,曹凯等[3]进一步研究制造商公平关切下供应链协调问题,并通过设计收益共享契约实现供应链各成员协调。一些学者从制造商和零售商对风险厌恶程度角度分析供应链成员间协调:张新和罗新星[4]基于前景理论探讨零售商不同风险偏好程度对供应链协调问题影响,而Zhou等[5]研究均衡条件下零售商静态和动态规避损失行为如何影响零售商决策、制造商利润和效用,单汨源等[6]基于制造商和零售商不同风险偏好进一步研究季节性产品供应链内部协调契约模型,Du等[7]基于各成员均为损失厌恶偏好下研究双方不同损失厌恶程度对其决策影响。此外,还有学者从政府激励[8]、激励成本分担[9]、库存竞争[10]、转移价格[11]等方面对供应链协调进行了研究,但均未涉及供应链间协调问题。

现代企业间竞争已转变为企业所在供应链间竞争,逐渐成为供应链管理领域最新研究方向[12]。Deng等[13]运用理论博弈模型,通过考虑供应链纵向一体化和横向一体化四种情形,探讨供应链竞争如何影响企业产品可持续性和利润策略;Chen等[14]研究需求不确定下两个竞争供应链中纵向和横向信息共享激励问题;李柏勋和林洁[15]基于供应链各节点不同议价能力研究链间不同博弈模型下各成员收益变化情况;Liu等[16]指出,大数据环境下供应链内各成员加强信息共享有助于提高链间竞争力;Ma等[17]基于时间概念拓宽了供应链间竞争维度。Wang等[18]引入产品绿色度分析两条竞争供应链间最优定价和生产决策,指出产品批发价与链间竞争强度呈反比;曹颖赛等[19]基于市场供求关系构建链内各成员博弈模型,在此基础上建立寡头市场环境下供应链间博弈模型;Wu等[20]考虑负溢出效应和服务竞争,构建供应链间双层复合嵌套博弈模型,指出链间竞争不利于提供服务的零售商;魏守道和孙铭[21]通过引入消费者补贴,探讨链间不同合作模式下供应链各成员利润及总利润变化情况。

上述文献分别从单链内各成员间协调和供应链之间竞争角度进行阐述,但通过梳理这些文献不难发现,学者们对供应链协调及定价问题已开展了比较系统研究,但对同时考虑供应链间竞争与链内各成员间协调相关问题研究不够深入,而在多供应链竞争环境下,对链内上下游企业间协调定价决策的有效刻画和分析,将有利于提高供应链协调运作水平和供应链总收益。本文考虑单一供应链内制造商和零售商选择策略与否,构建供应链间Stackelberg博弈,通过理论和算例分析,研究供应链内不同策略下供应链间定价和收益变化,期望厘清多链竞争背景下供应链内部协调定价机理和规律。

二、定价决策模型构建

1.问题描述

假设某寡头市场由两条生产可相互替代产品的供应链构成,且该产品在市场中已经饱和。供应链内核心企业零售商为领导者,制造商为追随者,且两者均有选择合作或非合作的权利;供应链间决策中,供应链1(SC1)为市场领导者,供应链2(SC2)为追随者,同时本文采用逆向归纳法求解博弈均衡[3]。考虑两条供应链都清楚博弈规则和结构,且皆以单链总收益最大化为目标进行博弈。为了分析比较,先构建链内制造商和零售商四种策略下总期望收益模型,再建立链间Stackelberg模型。链间竞争如图1所示。

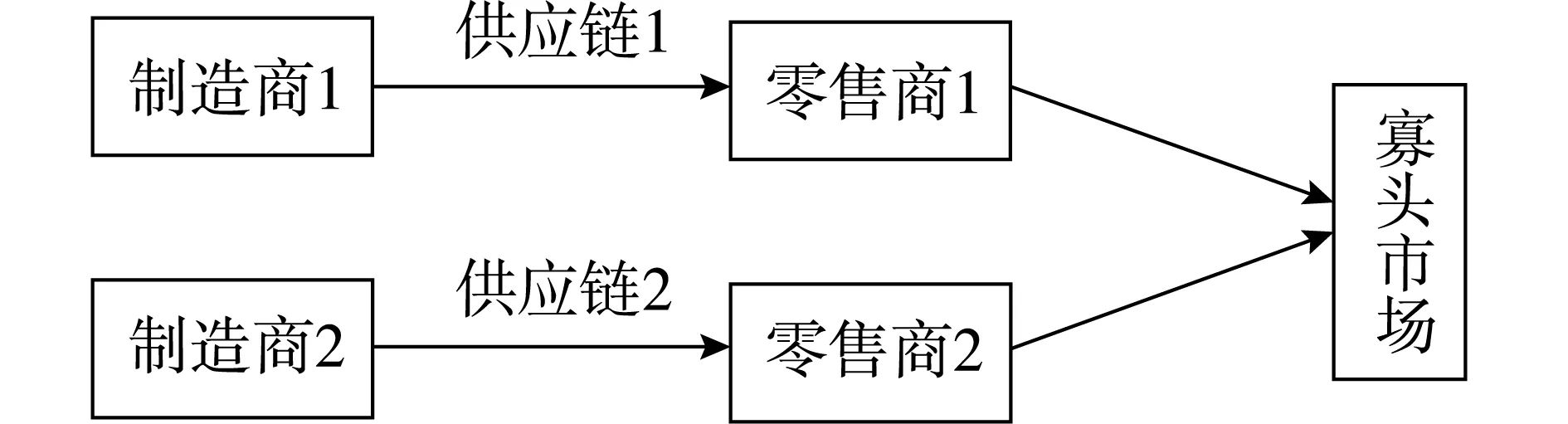
图1 两条供应链竞合示意图

2.链间Stackelberg博弈模型构建

基于市场中存在多链竞争特性,构建双供应链SC1和SC2间Stackelberg博弈模型。假设两条供应链都由单个制造商和单个零售商组成,链间同时采取同样策略,但任一链内各方具有选择合作或不合作决策的权利。链间博弈决策次序为:市场领导者SC1优先进行定价决策,而追随者SC2后定价。模型中涉及的具体变量及定义如表1所示。

表1 模型变量及说明

其中,i=1,2;j=3-i;λ=C,N;μ=CC,NN,NC,CN。此外,消费者对产品直接价格的敏感度大于交叉渠道的影响,即0<ηc,供应链内成员才倾向于采取合作策略。

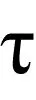
三、供应链间定价决策博弈过程分析

双链Stackelberg博弈模型中,领导者SC1零售商率先决策给出零售价格p1,追随者SC2零售商根据观察到的p1做出最优定价决策,制定出零售价格p2。链内制造商和零售商均具有采取合作或不合作决策的权利,且两条链同时采取相同策略,共有四种组合:同时合作(CC)、均非合作(NN)、制造商合作和零售商非合作(NC)、制造商非合作和零售商合作(CN),下面针对每种情况采用逆向归纳法对博弈过程进行分析。

1.制造商和零售商均采取非合作策略

供应链间Stackelberg博弈中,依据SC1零售商给出的零售价格p1,SC2零售商决定其零售价格p2;链内双方均选择非合作策略,不会产生协调成本和超额收益,本节研究可作为余下三种供应链协调策略情形的参照基准。

(1)追随者SC2链内动态博弈

依据SC1零售商给出的零售价格p1,SC2零售商给定零售价格p2,则SC2零售商收益函数如式(1)所示。

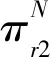
(1)

SC2制造商依据给定的批发价格,求出自身收益函数如式(2)所示。

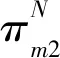
(2)

SC2总收益函数如式(3)所示。

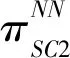
(3)

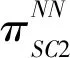
(4)

(2)领导者SC1链内动态博弈

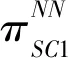
(5)

2.零售商采取非合作策略、制造商采取合作策略

此情形下制造商存在链内协调成本,但不会产生超额收益,链间Stackelberg博弈模型构建如下。

(1)追随者SC2链内动态博弈

SC2零售商收益函数同式(1),SC2制造商依据给定的批发价格,同时希望达成合作,存在一定的协调成本,则制造商收益函数如式(6)所示。

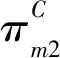
(6)

SC2总收益函数如式(7)所示。

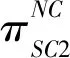
(7)

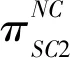
(8)

(2)领导者SC1链内动态博弈

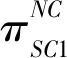
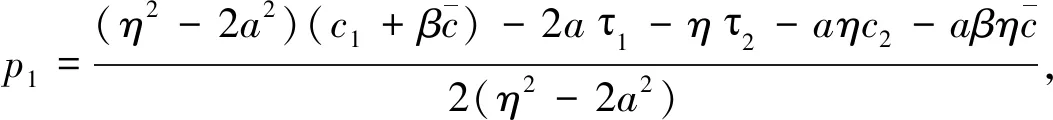
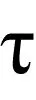
(9)

3.零售商采取合作策略、制造商采取非合作策略

此情形下零售商存在链内协调成本,但不会产生超额收益。

(1)追随者SC2链内动态博弈

链内零售商希望达成合作,会产生一定的协调成本,则SC2零售商收益函数如式(10)所示。

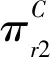
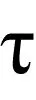
(10)

SC2制造商收益函数同式(2),SC2总收益函数如式(11)所示。

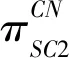
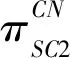
(12)

(2)领导者SC1链内动态博弈

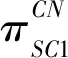
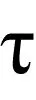
(13)

4.制造商和零售商均采取合作策略

此情形下制造商和零售商共同承担协调成本,并产生超额收益,链间Stackelberg博弈过程如下。

(1)追随者SC2链内动态博弈

链内双方均采取合作策略,会产生超额收益,则SC2零售商收益函数如式(14)所示。

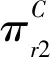
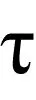
(14)

SC2制造商收益函数如式(15)所示。

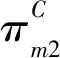
SC2总收益函数如式(16)所示。

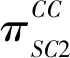
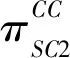
(17)

(2)领导者SC1链内动态博弈

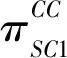
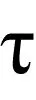
(18)

四、结果分析

命题1:四种策略下零售商价格在制造商和零售商选择合作策略时最小,均不合作时次之,制造商或零售商单方面合作下较大,其值视β大小而定。

命题1证明:

由命题1可知,四种情况下单链上零售价各不相同,为了共同收益最大,双方合作时都会作出让步,价格往往较低,这也符合实际情况;双方均不合作时,制造商和零售商为保证本方收益最大化,价格要高于前者,这也说明制造商或零售商单方面合作时,由于协调成本增加,选择合作方通过提高价格减少企业损失。

命题2:无论链内双方采取何种策略,领导者SC1的零售价均大于追随者SC2的零售价,即p1>p2。

命题2证明:

(1)链内零售商采取非合作策略、制造商采取合作策略

链内零售商采取合作策略、制造商采取非合作策略时证明过程类似,此处不再证明。

(2)链内制造商和零售商均采取非合作策略

(3)链内零售商和制造商均采取合作策略

由命题2知,追随者供应链零售价低于领导者供应链零售价,这表明后定价供应链可根据市场规模大小、产品替代率高低及初始投入成本大小等采取降低价格策略与先定价供应链竞争,从而获取较多客户需求,这也与实际情况相符。

命题3 无论链内双方采取何种策略,产品差异较小时,领导者SC1总收益均小于追随者SC2总收益。

命题3证明:

(1)链内双方均采取非合作策略时,把p1代入p2,得:

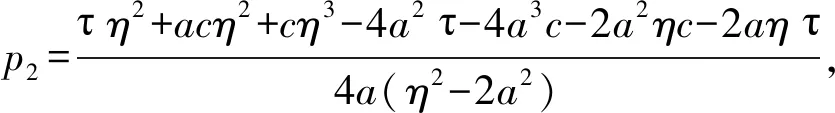
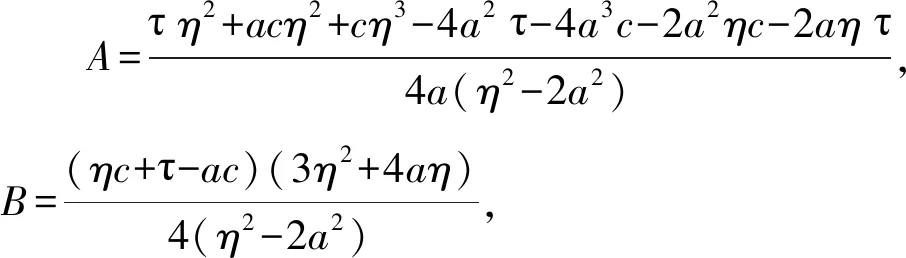
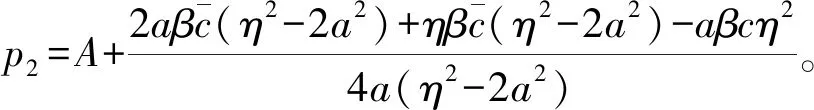
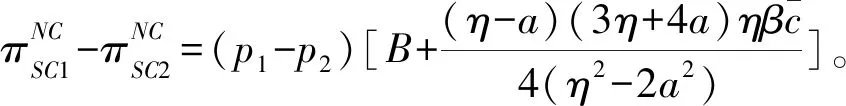
(3)链内双方均采取合作策略时,把p1代入p2,得:

比较领导者SC1总收益和追随者SC2总收益,得:

由命题3知,无论链内零售商和制造商采取何种策略,在链间Stackelberg博弈中,虽领导者SC1零售价高于追随者SC2零售价,但追随者可以通过降低价格、薄利多销等策略占领更多市场份额,导致领导者SC1所获总收益均小于追随者SC2,这也说明在产销相等、产品几乎同质情况下,虽领导者率先制定出符合市场行情的价格快速占领市场,但追随者根据产品可替代性或降低价格策略可以获取更大的收益。

五、数值仿真分析

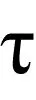
1.协调成本分担系数对单链零售价及总收益的影响

令β∈[0,1],根据链内零售商选择非合作策略、制造商选择合作策略,得到零售价格和单链收益如图2和图3所示。

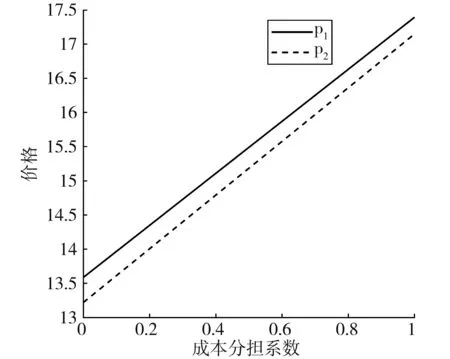
图2 价格随成本分担系数变化

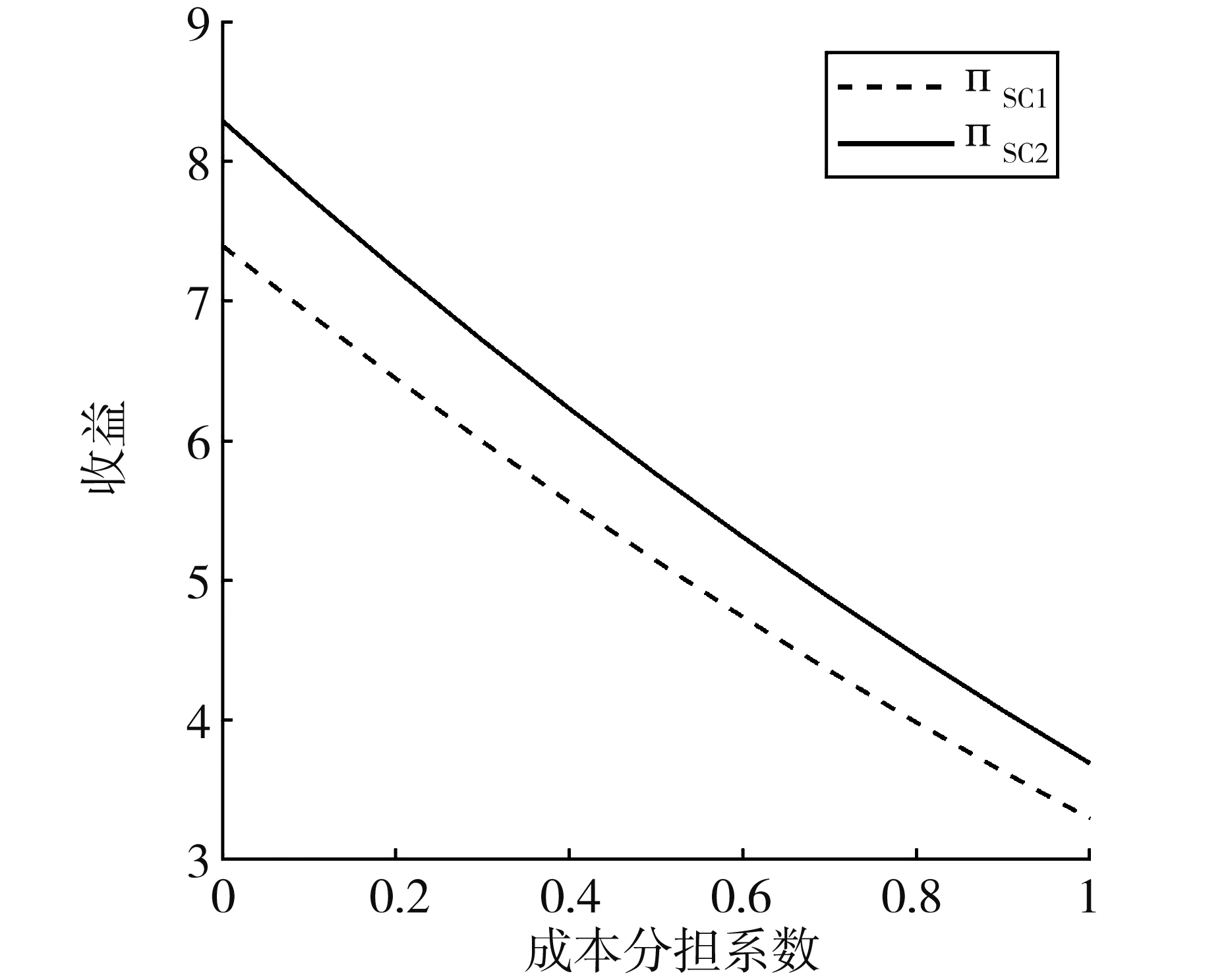
图3 收益随成本分担系数变化

由图2和图3可知,SC1和SC2零售价均与成本分担系数呈正比,各单链总收益均与协调成本分担系数呈反向变动,说明在产销量一定前提下,随着制造商或零售商分担协调成本增加,企业可通过提高价格弥补这部分支出,但整条供应链总收益仍呈下降趋势,这同时说明若链内双方对协调成本分配不合理,导致双方很难达成合作,进而影响整条供应链收益。链内零售商采取合作策略、制造商采取非合作策略情况类似,此处不再阐述;对于链内双方均不采取合作策略情况,因不产生协调成本,故对单链总收益不会产生影响;对于链内双方均采取合作策略情形,因所建模型中不含β,且各单链追求供应链总收益最大化,链内合作增加的总收益可以弥补产生的协调成本,故各供应链总收益均会有所增加,成本分担系数的变动对其影响甚微。

2.成本分担系数一定下,横向对比不同策略间定价和总收益

下面给定β=0.5,对比分析不同策略下各供应链价格及总收益,具体如图4所示,其中1-4分别代表NN、NC、CN和CC四种策略。

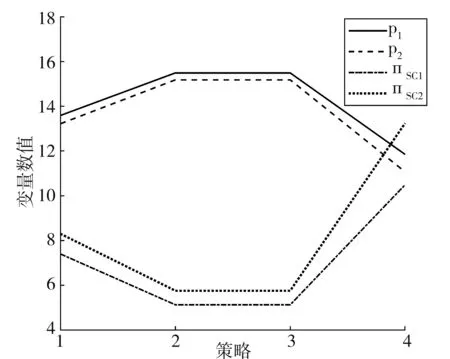
图4 不同策略下各变量数值

由图4可知:

(1)SC1或SC2零售价在制造商或零售商单方面采取合作策略时最高,均不采取合作策略时次之,双方采取合作策略时最小,这也表明若一方采取合作策略,必然导致该方协调成本增加,因此在产量一定前提下企业会通过提高价格弥补成本。

(2)两条供应链总收益在链内双方均采取合作策略时最大,均不采取合作策略时次之,链内一方采取合作策略时所获总收益最小,说明当链内双方均选择合作策略时,产生的超额收益可以弥补相应协调成本,双方都愿意适当降低价格以获取更多收益;链内制造商或零售商单方面采取合作策略导致协调成本增加,必然引起该方总收益降低。

(3)任何策略下领导者SC1零售价均高于追随者SC2零售价,而SC1总收益总小于SC2总收益,即p1>p2,πSC1<πSC2,这表明虽领导者率先进入市场,制定出符合市场行情价格、快速占领市场,获得一定领先优势,但后定价追随者可根据产品市场需求、产品替代率等适当降低价格,在产品几乎同质、差别不大情况下,能吸引更多需求、获得更多收益,对追随者供应链长期发展有利。

3.价格敏感系数和产品替代率对价格影响

令a,η∈[0,1],其他条件不变,双方均不合作情况下SC1和SC2零售价如图5所示。

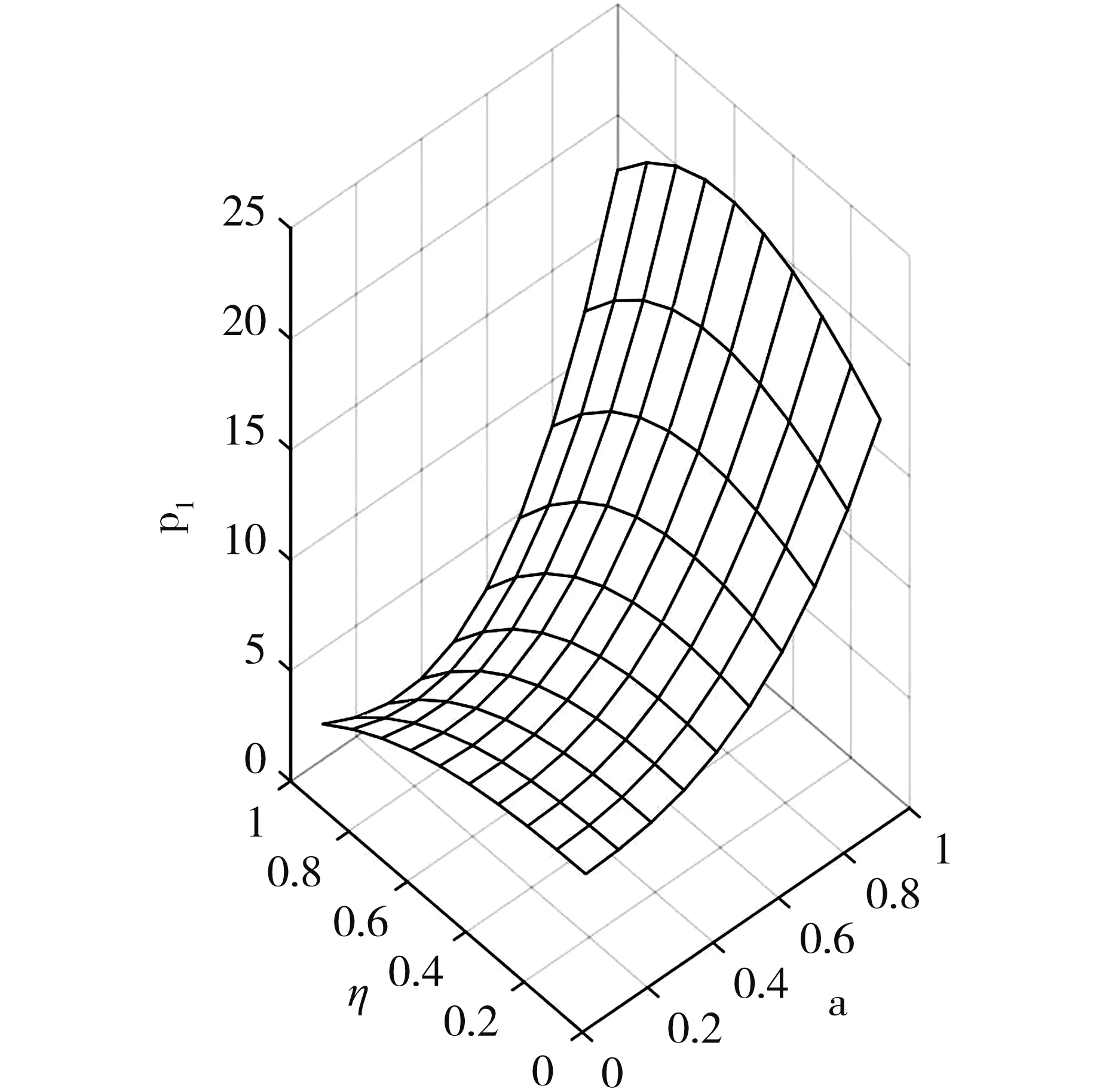
(a)第一种情形下零售商1价格

由图5可知,产品差异较大时,各供应链零售商价格均与顾客需求价格敏感系数呈正比,且SC1零售价变化幅度较大,原因是SC1率先进入市场制定价格,随着SC2在市场中所占份额增加,SC1会迅速提高价格以获得较多收益;产品几乎同质情况下,SC1零售价先下降再提高,SC2零售价与顾客需求价格敏感系数呈正比,原因是虽SC1率先进入市场,但由于后进者SC2产品与其差别不大,在消费者对价格不敏感前提下,SC1试图通过降价争夺市场份额;随着客户对价格敏感度提高,SC1和SC2均通过提高价格获取更多收益,但p1>p2,这也与上述讨论相符。其他三种情况类似,此处不再阐述。

六、结论

随着消费者超个性化需求激增,产品质量、服务和价格成为供应链间竞争核心,也对供应链定价提出更高要求。企业不仅需要在与同行竞争中生存,还需要不断提高产品质量和提供多样化服务,与供应链上下游企业建立合作关系就成为各企业甚至整条供应链保持竞争力的重要基础。本文通过构建两条包含单个制造商和单个零售商供应链,链内制造商和零售商均可采取合作或非合作策略,在两供应链不同主导地位下研究各单链最优定价策略。研究发现:链间Stackelberg博弈模型中,无论链内双方采取何种策略,领导者供应链零售价均大于追随者供应链零售价,而总收益则相反,说明即使领导者通过增产降价方式快速占领市场,但追随者根据产品可替代性或降低价格、薄利多销等策略获取更多收益,也说明在产销相等、产品几乎同质情况下,链间Stackelberg博弈中后定价供应链具有明显优势,对追随者供应链长期发展有利。通过数值仿真对所提模型合理性和有效性及相关命题合理性进行了验证。值得注意的是,本文考虑每条供应链仅包含单个零售商和单个制造商,但现实供应链可能包含多个节点,下一步考虑制造商和零售商上下游节点企业间竞合研究将更为有趣,此外新零售或区块链背景下供应链内协调也是未来研究方向。