基于PD理论和XFEM对混凝土板裂纹扩展仿真的对比分析

张富钧,王少雷,张玉栋,朱文明,崔义鑫

(河北建筑工程学院 土木工程学院,河北 张家口 075000)

混凝土材料构件在工程领域中应用广泛,项目中大多用作承重构件。由于混凝土结构的内部材料性质较为复杂,使用过程中易发生疲劳损伤,产生一些微细裂缝[1],破坏时没有明显预警,具有一定的安全隐患,尽管已经对混凝土结构破坏形式进行了大量的研究,但其渐进式破坏过程仍在工程中不可预测且不可控制,特别是对其裂缝的自发形成及其后续的裂纹扩展机制尚未完全了解[2-4]。如预先在裂缝扩展的路径上进行加固措施,将极大地降低工程事故的发生,故预测裂纹扩展路径是解决混凝土结构破坏的主要措施之一。

本文将基于近场动力学原理的混凝土板渐进破坏过程和基于扩展有限元法的混凝土板裂纹扩展方式进行对比分析研究,尽可能真实地模拟混凝土板的渐进式破坏过程,并与将两种渐进破坏进行对比和相互验证。

1 扩展有限元法

1.1 位移函数的确定

有限单元法在构件的位移场分析过程中具有连续性的特点,构件内部任意一点的位移表达如式(1)所示。

(1)

对有限元理论的局限性进行扩展研究,进一步将裂纹穿过单元内部,考虑构件的不连续性,在增加扩充项后,可将裂纹两端的不连续位移表达如式(2)所示。

(2)

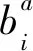
(3)

式(3)中,x是一个采样点;x*是距离裂纹上x最近的点;φ(x)是反映不连续性的强化函数,如式(4)所示。

(4)

式(4)中,(r,θ)表示以裂纹尖端为原点的局部极坐标,与标准有限元公式相比可以看出,在这种位移近似后,总体将增加6-7个自由度。

1.2 水平集法

在扩展有限元法的使用过程中,可采用水平集法来追踪界面破坏的演化,如图1所示。较传统有限元不同的是其网格的划分和断面间的位置相互独立,不需要重新划分网格就可以追踪其界面破坏的运动轨迹。裂纹面的水平集函数由以下符号距离函数表达,如式(5)和式(6)所示。

(5)

(6)

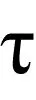
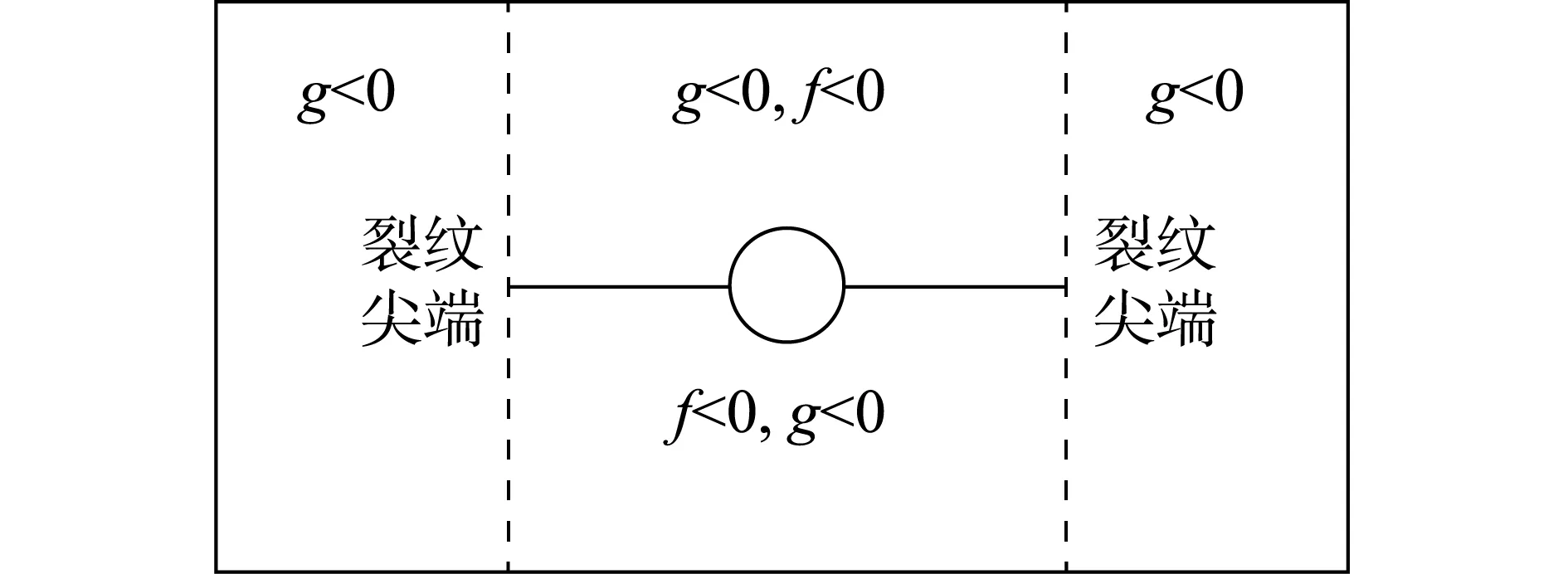
图1 界面破坏裂纹水平集定位图

1.3 扩展有限元仿真

1.3.1 仿真流程

通过在ABAQUS软件中对预制圆孔板进行破坏分析,建立混凝土预制板模型并引入材料属性和破坏参数,对预制板进行加载测试,并通过更改加载方向和施载大小,来模拟出混凝土板在工程中渐进破坏的裂纹扩展过程,扩展有限元仿真流程,如图2所示。

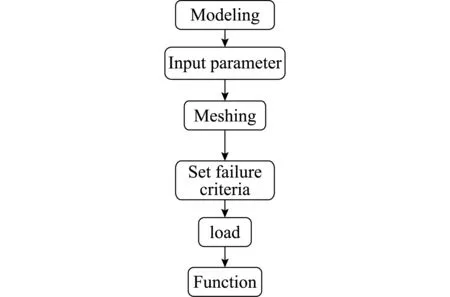
图2 仿真流程图

1.3.2 参数设置

通过ABAQUS建立三维预制圆孔混凝土板,预制构件的几何参数,如表1所示。在 XFEM的破坏演变中,为了更接近实际的混凝土板的内部应力破坏过程,需要对预制件的材料属性进行定义,输入参数如表2所示。

表1 几何参数表

表2 材料参数表

1.3.3 结果分析

模型施加载荷后,扩展有限元破坏图,如图3(a)所示,深色区域应力较大在裂纹尖端发生应力集中效应是渐进式破坏的主要原因,图3(b)为局部放大图,深色区域为应力集中点位置也是裂纹扩展的方向。

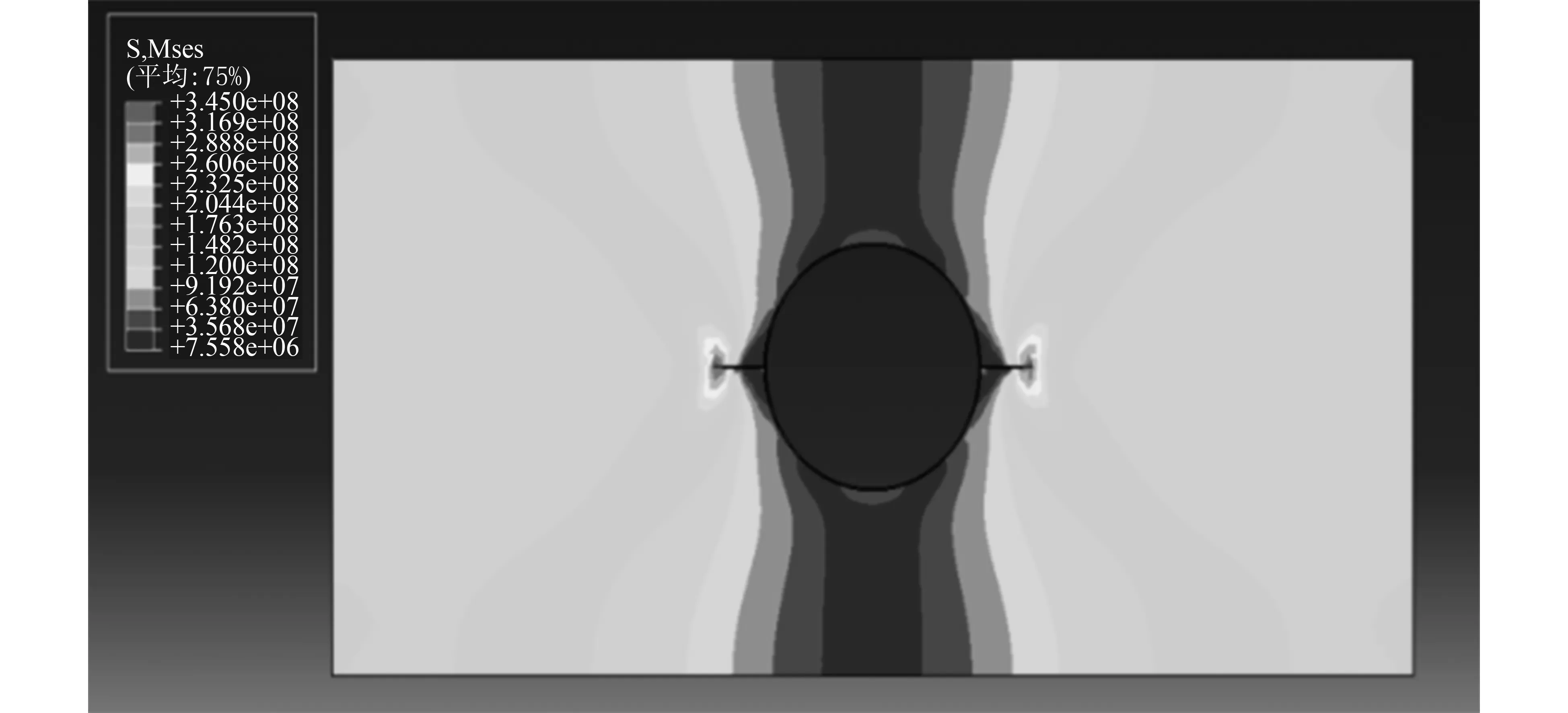
(a)裂纹初期萌生图

破坏过程中,裂纹尖端应力向周围逐步降低,初步破坏发生后产生大量的能量,裂纹逐步向板缘进行扩展,构件失效,致使混凝土板破坏,如图3(c)所示。得出结论应力集中位置往往是构件重点破坏区域,工程中应减少重要构件产生应力集中,或者加强材料的破坏极限逐步提高安全质量。

2 近场动力学

2.1 近场动力学理论

根据牛顿第二定律,可以列出物质点x在t时刻下的运动方程,如式(7)所示。

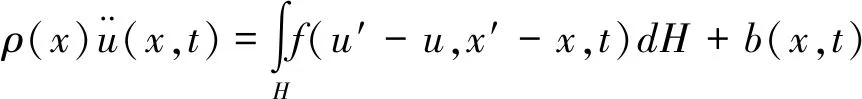
(7)

式(7)中,H为以δ为半径的圆域;u为位移矢量场;ρ(x)为物质密度;b(x,t)是体力密度;f为本构力函数:表示在t时刻下,单位体积的物质点X′施加于物质点X的体力密度/(N/m6),也称为力密度矢量。通常认为物质点X和X′存在相互作用力f,由两者自身的运动状态来决定,可以假设力密度矢量f与这些物质点之间的伸长率s呈线性关系,如式(8)所示[8-9]。

f(u′,u,x′,x,t)=f(u′-u,x′-x)

(8)

式(8)中,伸长率s(u′-u,x′-x)定义如式(9)所示。

(9)

式(9)中,s为t时刻键的伸长率;ζ用来判断物质点的破坏情况,定义如式(10)所示。

(10)

式(10)中,s0为物质点对的临界伸长率,在二维体系中,通常采用表达如式(11)所示。

(11)

式(11)中,k为体积弹性模量;μ为剪切模量;GC为临界能量释放率;δ为近场范围半径。当出现键的s≥s0时,该键断裂且永久失效,裂纹也随之产生,如图4和图5所示。

图4 键的伸长变化图

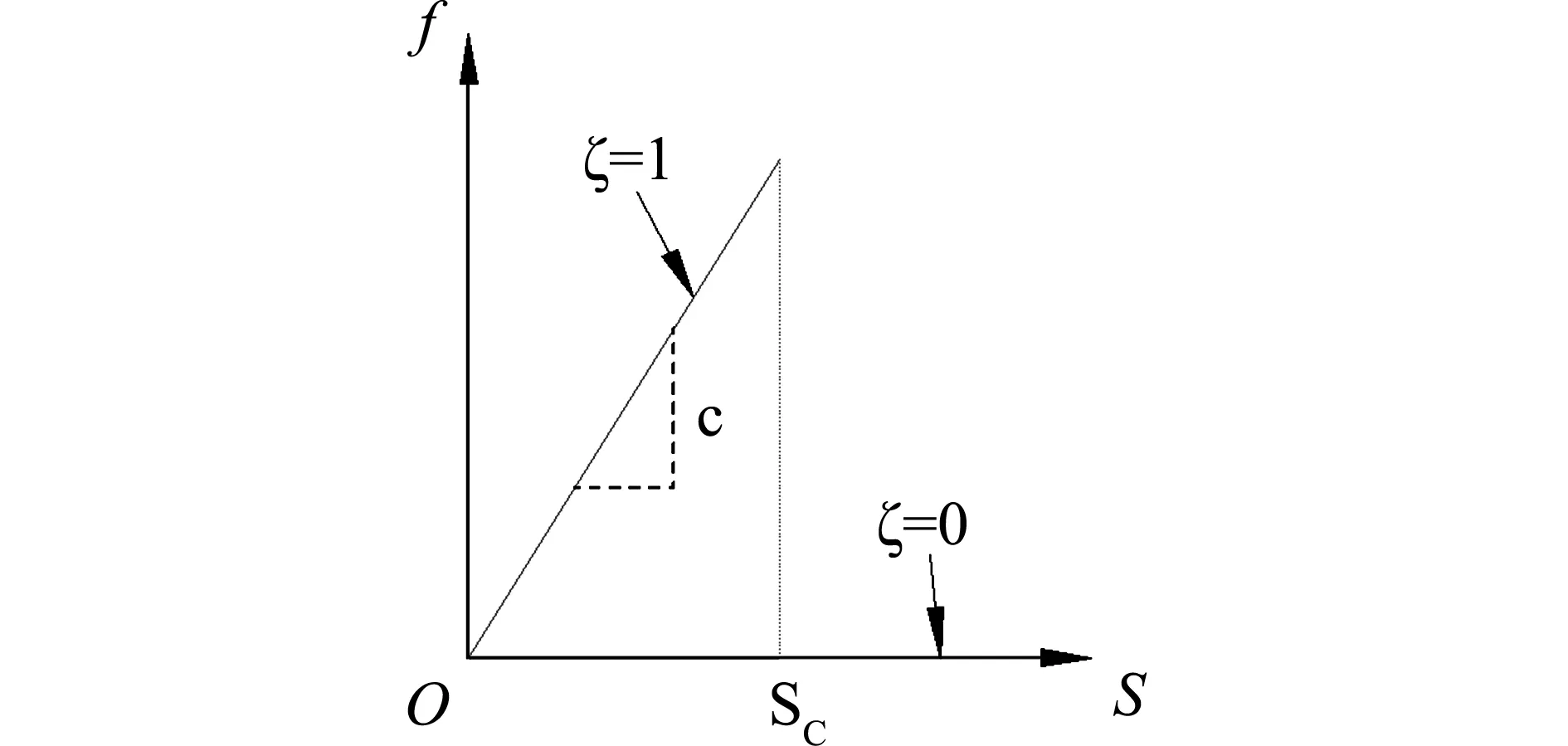
图5 伸长率和力密度矢量关系图

2.2 数值模拟

2.2.1 编码流程

在MATLAB软件中对混凝土板的裂纹扩展模型进行编码[10],如图6所示,初步设定材料参数,定义边界条件后,输入近场动力学破坏准则,在加载后对PD模型断裂进行判断,观察其完整的裂纹扩展演化。

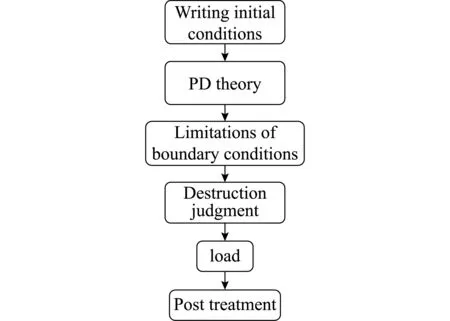
图6 编码流程图

2.2.2 参数设置

PD计算参数直接影响精度和效率,其域范围选取与材料的物理性质有关,当近场尺寸取3倍物质点间距时结果较为准确,故本文采取进场动力学范围δ=3Δ[11-15],PD模型的参数设置表,如表3所示。

表3 PD参数表

2.2.3 受拉荷载裂纹扩展

通过MATLAB软件进行编码,代码主要由初始参数、近场动力学理论公式、破坏准则、后处理四部分组成。通过编写基于近场动力学原理的预制圆孔混凝土板的破坏过程,输入混凝土和板的初始参数,并对域内键的连接数和加载值进行破坏分析,观察预制圆孔板在不同材料下的渐进破坏时间和破坏趋势,并设置破坏规则,在加载过程中观察其混凝土板的破坏过程,通过模型的运行时间和板的破坏趋势来对模型进行分析,确定开裂的载荷,并更改域内键的数量和施加荷载的大小来观察预制板的破坏形式[15-18]。

在运行MATLAB程序代码后,输出破坏图像,本案例计算耗时127秒,如图7所示。

(a)初始图

由图7(b)得出裂纹在荷载的加载方向垂直发生扩展[18-22],预制圆孔水平方向产生应力集中效果。圆域中的两物质点发生相对位移变化,当伸长率大于临界伸长率时发生断裂,且断裂产生后是不可恢复,通过初次横向裂纹的产生,圆域内的各点处于动态变化中,键长在不断地更新,裂纹逐渐扩大,直至预制圆孔的混凝土板的近场动力学破坏终止。含预制圆孔的混凝土板近场动力学破坏预测的结果图,如图7(c)所示,裂纹的破坏具有一定的趋势,裂纹的大小也在逐步扩大,在混凝土板的四个直角位置也发生破坏,可见直角处也是发生应力集中破坏的要点之一。得出结论,当物质点对之间的连接键超过临界伸长率时,物质点间会发生破坏效果,在不同时间步的检测下,裂纹在不同速度边界条件下的应力集中处发生破坏,利用近场动力学方法将宏观材料渐进破坏过程模拟出来。

2.3 图像分析

x=0,y=0.01处质点位移分量ux和uy的收敛性分布图,如图8所示,随着时间步数的增加,在x=0,y=0.01处的质点在x方向的位移和y方向的位移快速收敛,逐步趋于稳定值。总时间步长为2000时,可得出较为收敛的解。

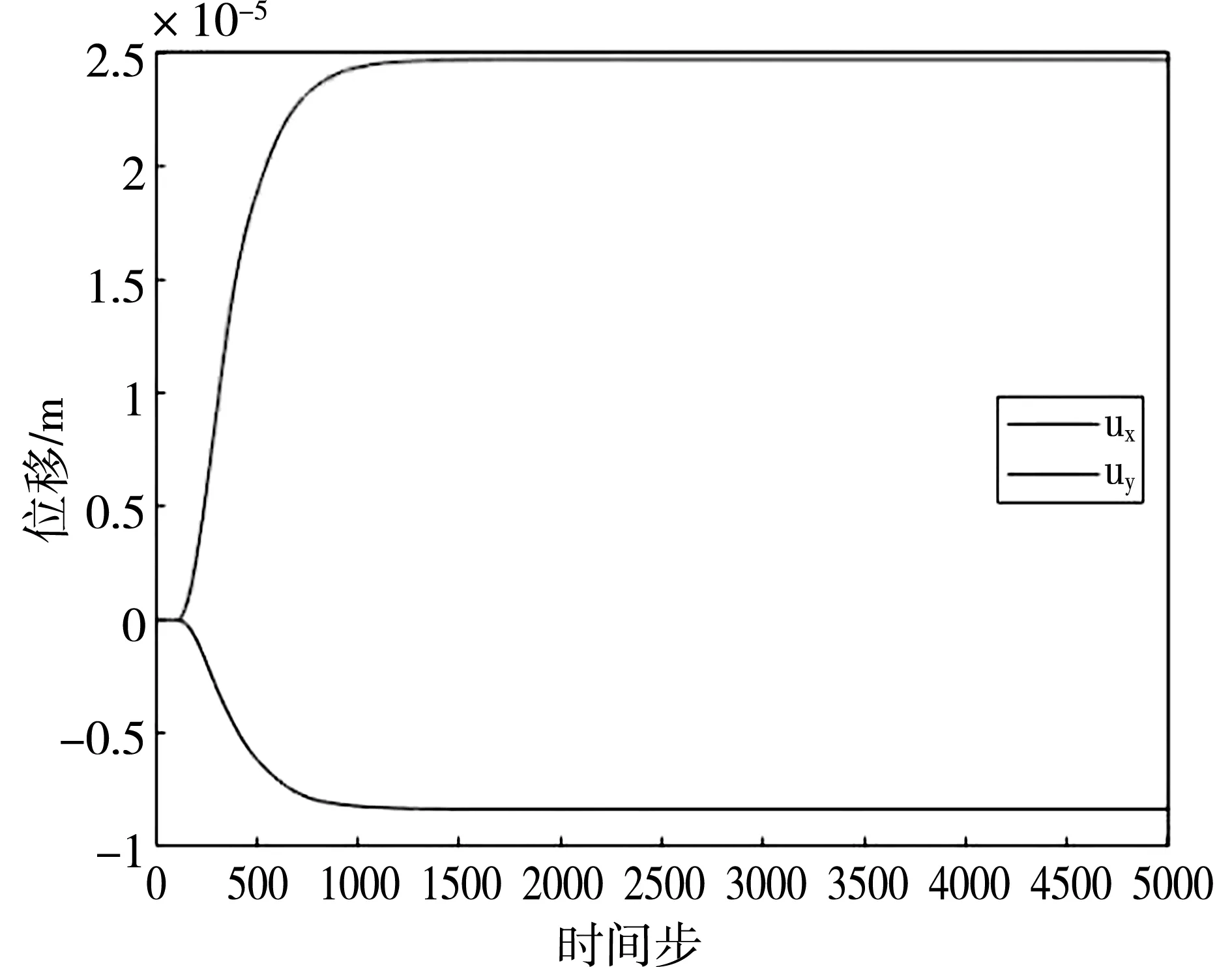
图8 x=0,y=0.01处质点位移分量ux和uy的收敛性

单轴拉伸载荷下平板中心线上的位移图,如图9所示,在单轴拉伸载荷下,对平板中心线上的位移进行分析,并将ux和uy处的PD解和解析解对比,可见PD解和解析解的结果吻合。

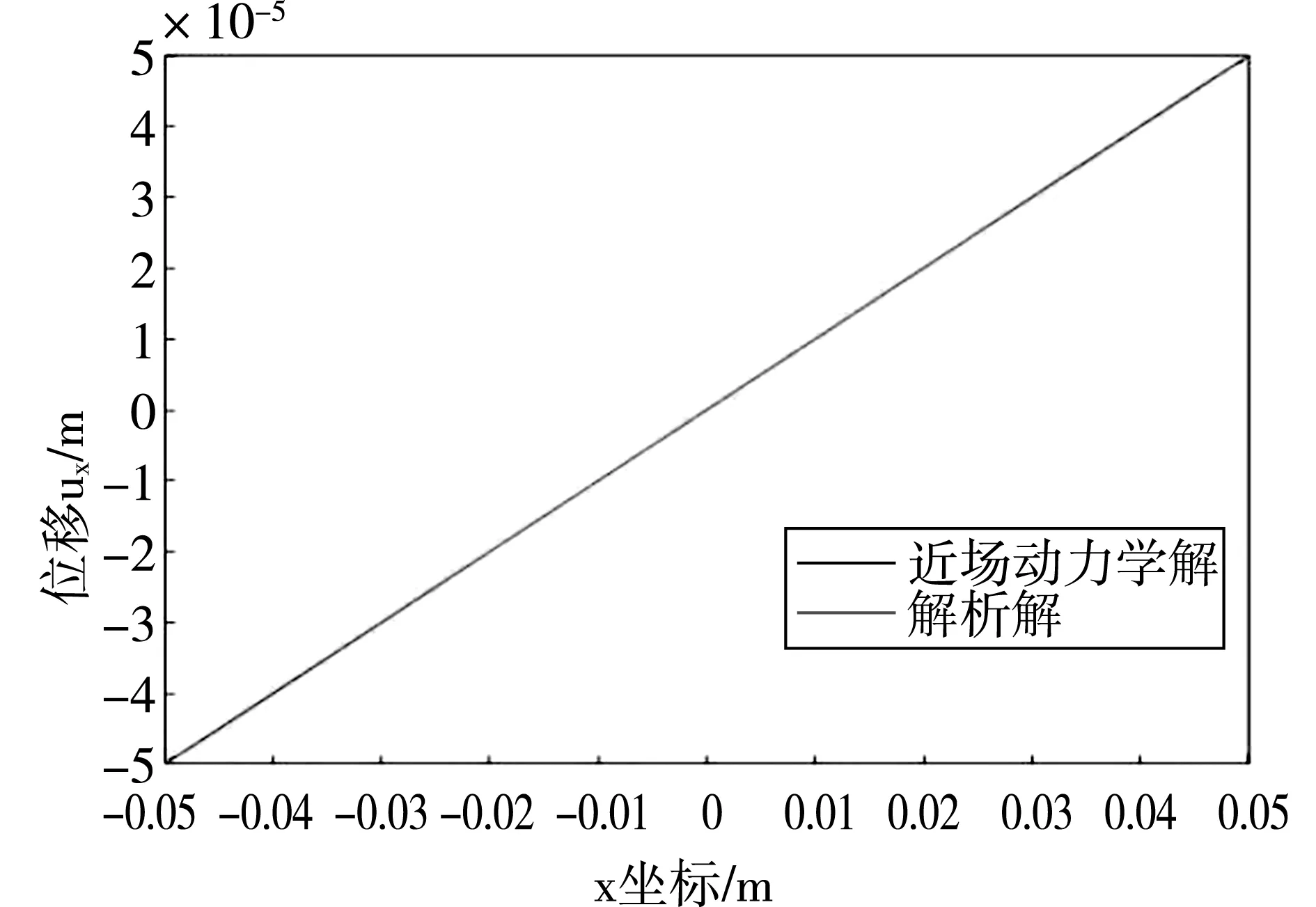
(a)x坐标

结语

(1)本文对混凝土板单轴受拉载荷的动态破坏过程进行模拟观测裂纹的扩展趋势,利用PD和XFEM两种方法对不连续介质渐进破坏过程进行模拟,对比得出PD理论在模拟裂纹扩展方向上更有优势,将两者的分析结果进行结合,可以更加准确地对单轴拉伸载荷下的混凝土板的破坏机制进行预测,工程应用中,如在裂缝易发生区域和裂缝扩展区域进行加固措施,或者改变拉应力的施加区域,可以控制裂纹的产生和裂缝的不规则扩展趋势,提高了一定的安全保障。

(2)PD理论和XFEM均可对混凝土板的渐进破坏进行模拟,PD理论在计算和建模仿真上较优于XFEM,PD理论可以直接应用于不连续介质中,在模型计算中近场动力学相较于XFEM法不会出现不收敛的情况,并且PD理论中已有损伤和断裂的标准,在分析破坏和裂纹扩展情况时,不需要经过传统的开裂判断和裂纹路径预测等分析,通过连接键的断裂来控制裂缝产生,可自发地产生裂纹,并且裂纹在键的断裂后完成裂纹扩展,且在计算方法和耗费的计算资源上更为简单和快捷。