基于堆叠模型的滑坡易发性评价
——以商洛市丹凤县为例
郭亚雷,邓念东,李宇新,周 阳,石 辉
(1. 西安科技大学 地质与环境学院, 陕西 西安 710054; 2. 陕西省地质调查院,陕西 西安 710043; 3. 陕西省水工环地质调查中心,陕西 西安 710068)
0 引言
滑坡作为严重的自然灾害,对人们的生命和财产安全造成了巨大的威胁[1-2]。滑坡易发性评价指一定区域内滑坡发生可能性的预测,被认为是对区域滑坡进行防治措施的首要步骤以及土地空间规划的有效借鉴。因此,科学严谨、高精度的滑坡易发性评价意义重大。目前,国内外学者已进行大量滑坡易发性评价相关的研究,评价方法主要包括定性和定量2种方法,随着评价方法研究的深入,定性方法展现出主观性大的缺点,逐渐被定量方法所替代[3]。随着计算机人工智能的飞速发展,一系列经典的机器学习与数据发掘算法已经应用至滑坡易发性评价,并取得了较优的预测结果,诸如人工神经网络[4]、支持向量机[5]、朴素贝叶斯[6]、决策树[7]等。田述军等[8]基于不同评价单元,论述了斜坡单元和网格单元对滑坡易发性评价结果的影响。李文彦等[9]对滑坡易发性不同评价模型进行对比,并验证了各模型的精度。由于滑坡发生机理复杂,影响因子数据与标签的关系通常呈非线性,以上机器学习算法在分析不同区域时仍存在一定适用性的差异,并且过拟合是机器学习算法进行分类时难以规避的问题。集成学习是指将多个分类器组合来共同解决分类或回归任务的模型,分类器组成结构主要分为同源集成与异源集成2类[10]。研究表明,集成学习能有效克服单一机器学习模型自身的局限性,具有更高的泛化能力[11]。其中Adaboost[12]、Bagging[13]、随机子空间(random subspace, RS)[14]、随机森林[15]等集成学习方法已应用于国内外滑坡易发性评价研究中。为弥补不同集成学习各自预测的缺陷,堆叠Stacking模型可将多种模型进行组合,从而提高分类精度。同时,非滑坡的选取影响着样本数据纯度,文中对评价因子进行滑坡密度分析与筛选,在滑坡分布稀疏的区域与缓冲区叠加选取负样本。
1 研究方法
1.1 RA模型
RA模型属于Boosting算法族,由于Boosting算法通常使用弱分类器,使得其个体学习器之间存在强依赖关系。 RA是Freund和Schapire提出的一种解决二分类问题的集成学习算法。主要目标为将弱学习器“提升”为强学习器,其核心思想是根据训练集的权值分布来选择各分类器所使用的子集,对权值进行调整。对集成系统中各个分类器的分类结果使用加权多数投票进行组合,使具有较高训练精度的基分类器在投票时具有更大的权重,具体流程为先对每个样本赋予相同的初始权重,每一轮学习器训练过后都会根据其表现对每个样本的权重进行调整,增加对分错样本的权重,从而在后续训练中加强对分错样本的学习,按这样的过程重复训练出多个学习器,进行加权组合。最后将对应的权值之和最大的那个类别作为分类结果(图1)。
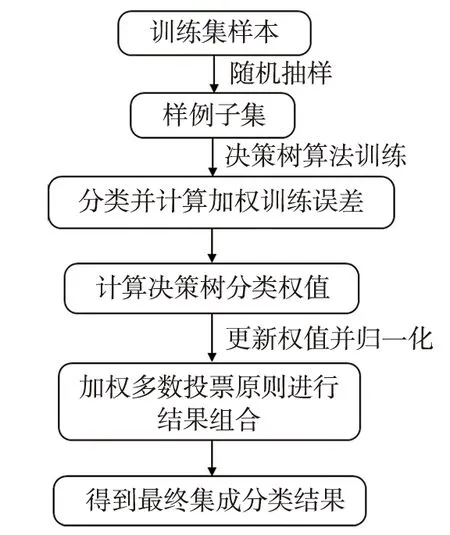
图1 RA模型分类流程图Fig. 1 Classification flow chart of RA model
1.2 DECORATE模型
DECORATE(diverse ensemble creation by oppositional relabeling of artificial training examples,DECORATE)是Melville和Mooney在2005年提出的一种集成学习算法,属于同源集成的一类。与Bagging和Boosting算法族的一个显著的区别是,该算法的基本思想是通过利用人工训练样例集来生成一些多样化的分类器。研究表明,DECORATE比Boosting对冗余样本数据具有更强的鲁棒性,比Bagging对缺失属性值样本具有更好的容忍性[16]。该算法首先统计训练集的分布特征,对于连续性属性计算其均值与标准差,基于这2项指标得到一定人工样本数据;对于离散值统计其出现的频率,根据频率同样随机选取一定量数据。对上述人工样本数据通过概率元组的方式进行类别标记,由于类标签与集成系统分类结果的差异,促进了其个体分类器之间多样性。在每次迭代中,在扩展训练集生成一个分类器后,将扩展集成系统与原集成系统分类的训练精度进行对比以及不断进行筛选,来保证该模型分类精度不会降低。
1.3 RS模型
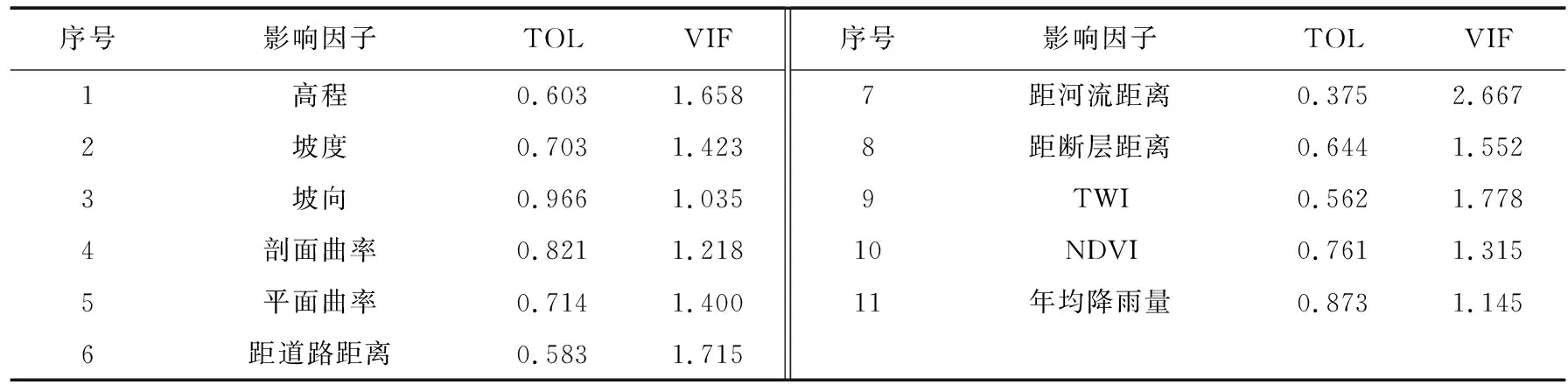
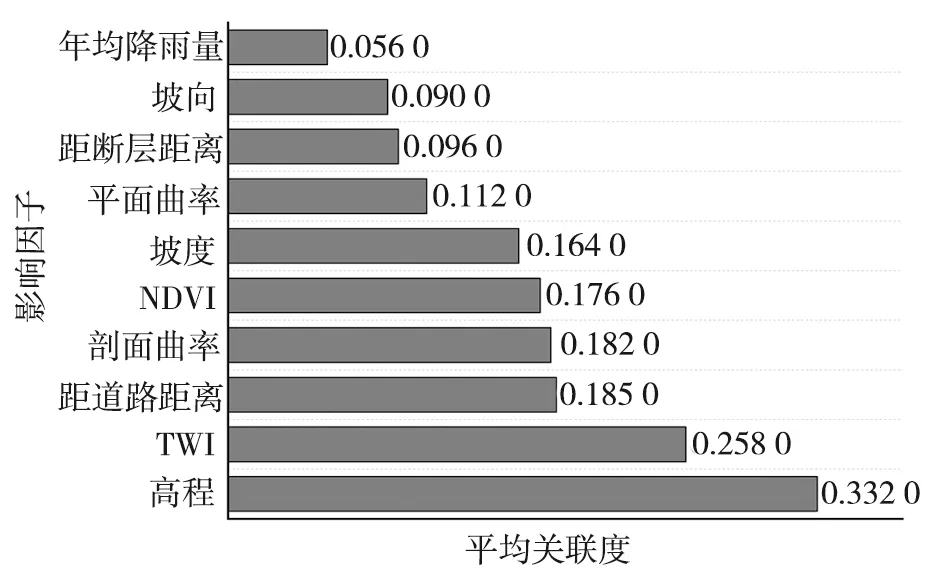
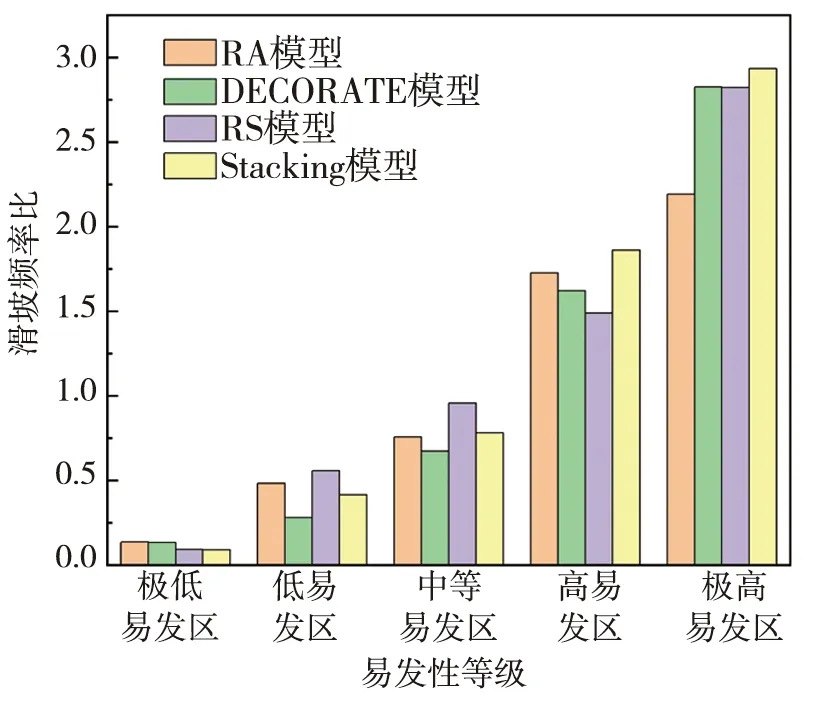
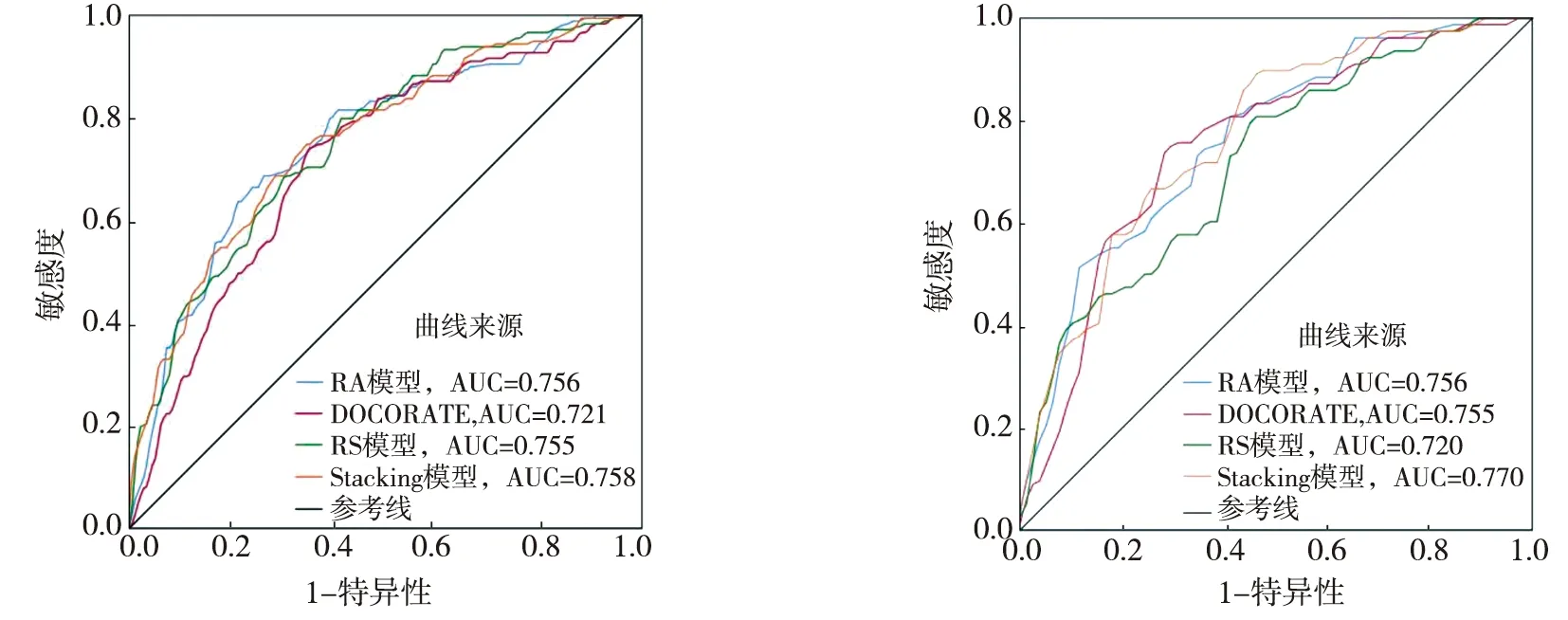
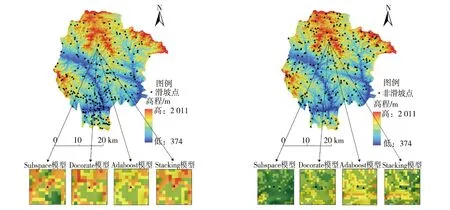
RS模型隶属于Bagging算法族的一类,是基于对训练集随机抽样的一类集成学习算法[17]。首先,从训练集的属性集合(A1,A2,…,An)随机选取k个属性(1 随机森林主要是通过多棵决策树中每棵树的投票结果来获取最优的分类结果。每棵决策树因有回放的方式以及随机获取数据特征所得到的数据集而具备更全面的输入变量信息。通过多棵决策树的集成来实现模型的鲁棒性并避免过拟合。随机森林主要特征是能够给出相应输入变量的重要性排序。随机森林中用不纯度来度量最佳分割,通过环境因子k在节点分割时的基尼指数的减少值DGk实现基础环境因子重要性计算,其中涉及平均基尼减小值占所有基础环境因子平均基尼减小值综合的百分比计算,具体如式(1): (1) 式中:m,n,t分别为基础环境因子总数、分类树棵数和单棵树节点数;DGkhj为k个因子在第h棵树的第i个节点上基尼指数减小值;Pk为第k个基础环境因子的重要性。 Stacking模型是一种异构分类器集成的模型,这是与同源集成模型主要的区别。模型由2层框架组成:第1层由RA、DECORATE、RS多个基分类器组成;第2层为处理第1层输出结果的元分类器。首先将数据集分成训练集和测试集,利用训练集训练得到多个初级学习器,然后用初级学习器对测试集进行预测,并将输出值作为下一阶段训练的输入值,最终的标签作为输出值,用于训练次级学习器,再让次学习器给基分类器模型的结果分配权重,进行重复训练后,将10倍交叉验证后的基分类器训练结果的概率分布,作为元分类器线性回归模型的输入,线性回归模型对每个类学习了一个分类结果隶属度的线性回归函数,归一化后作为分类概率,最后得到集成模型的分类结果(图2)。由于每次所使用的训练数据不同,因此可以在一定程度上防止过拟合。 图2 Stacking模型流程图Fig. 2 Flow chart of Stacking model 丹凤县位于秦岭东段南麓, 地处陕、 豫、 鄂三省交界之丹江通道上段。县域东西长62.1 km, 南北宽 65.5 km,总面积为2 438 km2。属于北亚热带向暖温带过度的季风性半湿润山地气候区,气候温和,四季分明,平均气温13.8℃,年平均降雨量687.4 mm,年日照时间2 056 h,无霜期217 d。地势西北高、东南低,高程介于324~2 011 m,相对高差1 687 m,县域内分布着自北而南的3条山脉;发育有丹江、银花河、武关河和老君河4条河流河谷相间,呈“掌”状地貌。通过研究区地质灾害详细调查,共圈定257处滑坡,通过GIS转化为点映射至区内(图3)。 ①优:骨折完全愈合且功能正常,无痛、无畸形,生活自理能力同骨折前。②良:骨折愈合,无痛、无畸形,但存在10°~20°活动度之差,生活能自理。③可:骨折略有畸形愈合,无痛,功能有所恢复,生活可部分自理。④差:骨折愈合延迟,有疼痛感,功能受限,生活不能自理。 图3 滑坡编录图Fig. 3 Landslide cataloging diagram 文中通过“地理空间数据云”获取研究区DEM数字高程数据和Landsat 8遥感卫星数据;利用Bigemap地图软件下载1∶5万地质图以及道路、水系矢量数据。根据DEM数据在ArcGIS软件中生成坡度、坡向、曲率、地形湿度等指数因子,为模型数据库的构建奠定基础。 选取合适的评价单元是滑坡易发性评价的基础,主要划分为栅格单元、斜坡单元、地形单元[18]。由于栅格单元具有数据结构简单、计算机处理高效的特点,更适用于集成学习模型的训练与验证。根据汤国安经验公式[19],文中采用30 m×30 m大小的栅格作为评价单元,将研究区共划分为2 670 541个栅格。结合研究区地质环境背景,初步选取高程、坡度、坡向、剖面曲率、平面曲率、TWI、NDVI、距河流距离、距道路距离、距断层距离、地层岩性和年均降雨量共12个影响因子。对连续型因子分别采用Jenks自然间断法和等间距法进行分级;离散型因子根据二级因子类型进行划分(表1)。 表1 滑坡密度分析结果Table 1 Landslide density analysis results 续表 集成学习训练与验证的数据库由正负样本组成,通常将滑坡影响因子数据作为正样本,选取等量的非滑坡区域提取负样本数据。因此,非滑坡区域的选取直接影响到模型拟合的效果[20]。目前,主要有以下选取方法:1)在滑坡周界外一定距离作缓冲区处理,在其余范围进行随机选取。该方法不足之处在于不同研究区缓冲区阈值难以确定。2)在特定的非滑坡区域进行选取,比如水系区域、坡度小于2°的区域等[21]。该方法存在负样本选取集中、数据覆盖不全面的问题,易造成分类模型过拟合,从而导致结果准确率降低。 为有效避免因数据冗余造成模型分类精度下降,以及非滑坡因子属性集中造成的过拟合问题,文中通过统计各因子二级分类的滑坡数量与滑坡密度(表1),剔除滑坡数量与密度同时最高的二级分类范围,选取其余区域与剔除滑坡缓冲区范围进行叠加,选取范围如图4所示。在该区域随机生成257个非滑坡点并提取因子属性信息。将正负样本按照7∶3随机划分为训练集与验证集,分别包括179和78个样本。 图4 非滑坡选取范围Fig. 4 Selection range of non-landslide 在R语言中利用随机森林模型计算出各因子的权重值,对12个因子进行重要性排序,结果见图5。筛选出的高程、坡度、坡向、剖面曲率、平面曲率、距道路距离、距断层距离、距河流距离、TWI、NDVI、年均降雨量、地层岩性12个重要因子中,地层岩性权重值为0.029 8,远小于其他类因子权重值,其重要性最低,因此剔除影响较弱的地层岩性因子。 图5 各因子权重分布图Fig. 5 Weight distribution of each factor 对模型的训练集进行相关性和共线性分析,可以降低因数据间高度相关或共线对模型分类精度的影响。文中采用皮尔逊相关性(PCC)、方差膨胀因子(variance inflation factor, VIF)和容忍度(tolerance, TOL)进行分析,其中TOL为VIF的倒数。通常认为PCC大于0.5或VIF大于2时,数据之间存在较强烈的相关性或较严重的共线性,需要进行剔除[22]。同时采用相关属性评估(correlation attribute evaluation,CAE)进行10倍交叉验证,分析研究区滑坡发生的关联度,其值越大代表该因子与区内滑坡发生更密切。 由表2和表3结果可以看出,距水系距离与距道路距离的皮尔逊相关性为0.591,同时距水系距离VIF值为2.667,因此剔除距河流距离因子。根据图6分析结果,其余10个因子对研究区滑坡均有一定作用。最终选取高程、坡度、坡向、剖面曲率、平面曲率、距道路距离、距断层距离、TWI、NDVI、年均降雨量共10个因子作为一级指标进行评价。 表2 皮尔逊相关性指标Table 2 Pearson correlation indicators 表3 影响因子共线性分析Table 3 Collinearity analysis of impact factors 图6 影响因子CAE分析Fig. 6 CAE analysis of impact factors 文中采取的基分类器分别为RA、DECORATE和RS模型,均在WEKA3.8软件中进行生成。对RA模型进行参数设置,其中选择决策树为基分类器,迭代次数为100次,收缩参数为0.1;DECORATE模型选择J48树算法为基分类器,其中用于剪枝的置信因子设为0.25,成员分类器数量选择15个,迭代次数为50;RS模型采用REP树模型作为基分类器,每一个子空间大小为0.5,迭代次数为100。将训练集代入RA、DECORATE和RS这3种集成模型中,通过10倍交叉验证分别得到训练正确率为74.7%、69.9%和74.9%,代入验证集数据得到预测率分别为76.5%、73.8%和72.6%。最终,将研究区11个因子属性的2 670 541个栅格代入3种模型生成滑坡易发性指数(landslide susceptibility index, LSI)。根据自然间断法,将LSI分为极低易发区、低易发区、中等易发区、高易发区和极高易发区5类[23](图7)。 同样采用WEKA软件构建Stacking模型,其中基分类器使用上述RA、DECORATE以及RS模型,分类器参数选择与单独训练时一致;元分类器选用线性回归模型。通过10倍交叉验证进行训练,得到训练正确率为75.5%。代入验证集数据得到预测率为77.1%,最终生成研究区各栅格LSI值,重分类生成滑坡易发性分区图(图8)。 通过比较4种模型滑坡易发性分区结果,可以看出区域等级划分趋势基本一致。极高易发区主要集中在研究区中南部,极低易发区主要分布于研究区北至东北部。图9对4种模型易发性分区进行统计,从各易发性等级对应的滑坡密度可以看出,4种模型滑坡频率比均随着易发性等级提高而上升,说明分区结果与事实相符。其中,Stacking模型高至极高易发区的滑坡频率比为2.932,高于其余模型(RA模型为2.192,DECORATE模型为2.825以及RS模型为2.821),说明Stacking模型对研究区滑坡预测更为敏感。 图9 滑坡易发性等级分区对比Fig. 9 Comparison of landslide susceptibility grade zones 文中采取受试者工作特性曲线(receiver operating characteristic,ROC)及其线下面积(area under curve,AUC)对4种模型训练与验证进行对比[24]。ROC曲线以敏感度(即实际为滑坡,预测为滑坡)为纵坐标、1-特异性(即实际为非滑坡,预测为滑坡)为横坐标,通过动态分类阈值避免界限值对结果的影响[25],如图10、图11所示。 图10 训练集ROC曲线 图11 验证集ROC曲线Fig. 10 ROC curve of train set Fig. 11 ROC curve of validation set 从图10、图11中可以看出,4种模型训练与验证集AUC值均大于0.7,表征其预测能力均较好[26],其中集成了3种基分类器的Stacking模型AUC值高于其余单独分类器模型,说明不同集成模型作为基分类器组合成的Stacking模型泛化能力更好。 文中分别选取滑坡点和非滑坡点对Stacking模型及其基分类器的效果进行了对比,图12为滑坡点及其周围模型易发性结果对比,Stacking模型预测的易发性为极高易发、高易发;RA、DOCORATE及RS模型预测出的易发性为高易发、中等易发;图13为非滑坡点及其周围模型易发性对比结果,Stacking模型预测出的易发性等级为极低和低;RA、DOCORATE及RS模型预测出的易发性等级为低和中等。结果发现,Stacking模型在易发性预测中,与历史滑坡分布更加吻合,说明其更适用于研究区滑坡易发性评价,其易发性分区结果可以作为相关部门进行土地规划与滑坡防控的参考依据。 图12 单个滑坡点易发性等级对比 图13 单个非滑坡点易发性等级对比Fig. 12 Comparison of susceptibility grades of single landslide points Fig. 13 Comparison of susceptibility grades of single non landslide points 文中以Stacking模型进行丹凤县滑坡易发性评价,提供了一种新的评价方法与思路,仍存在一些问题将在后续深入研究:1)文中以集成学习的分支选取RA、DECORATE和RS模型,尚未进行基分类器数量与种类差异对堆叠效果影响的研究,来提升Stacking模型的泛化能力;2)文中基分类器参数主要依靠试验确定,存在一定主观性,后续可进行模型参数的优化选取,提高模型预测精度。 文中采用Stacking集成模型进行了丹凤县滑坡易发性评价,有以下结论: 1)结合相关文献及地质资料,文中选取高程、坡度、坡向、剖面曲率、平面曲率、TWI、NDVI、距水系距离、距道路距离、距断层距离、地层岩性和年均降雨量共12个影响因子,CAE结果显示其均对研究区滑坡具有关联性,其中高程、TWI和距道路距离与滑坡发生最为密切。区内滑坡主要集中发生在高程介于374~720 m、TWI介于8.88~12.55以及距道路距离介于3 108.58~5 364.30 m的区域中。通过VIF和皮尔逊相关性进行因子相关性分析和随机森林计算各因子权重,剔除距水系距离、地层岩性因子后选择剩余10个因子构建模型数据集。 2)通过WEKA软件分别构建了单一的RA、DECORATE、RS模型以及基于前三者的Stacking集成模型。训练与验证结果表明4种模型AUC值大于0.7,4种模型均具有良好的预测能力,其中Stacking模型较其他单一模型相比,训练成功率与验证预测率均最高,为国内滑坡易发性评价的模型选择提供了新的思路。 3)4种模型的滑坡易发性分区图划分趋势基本一致,研究区滑坡高至极高易发区主要分布于研究区中南部,低易发区分布于北至东北侧。通过等级分区统计,Stacking模型的滑坡高至极高易发区滑坡频率比达到2.932,高于3种单独模型,表明其分区结果与历史滑坡分布最为吻合。研究结果可作为相关部门进行滑坡防治与土地利用的参考。1.4 随机森林模型
1.5 Stacking模型
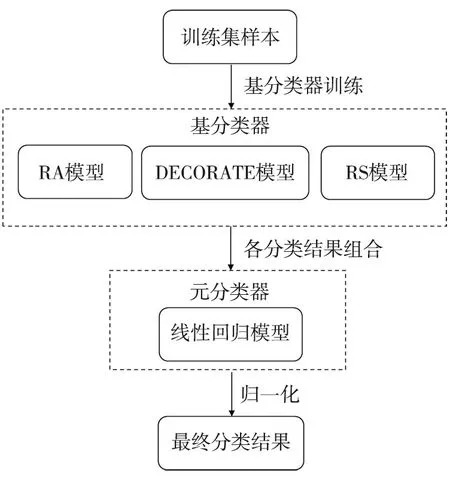
2 研究区概况及数据源
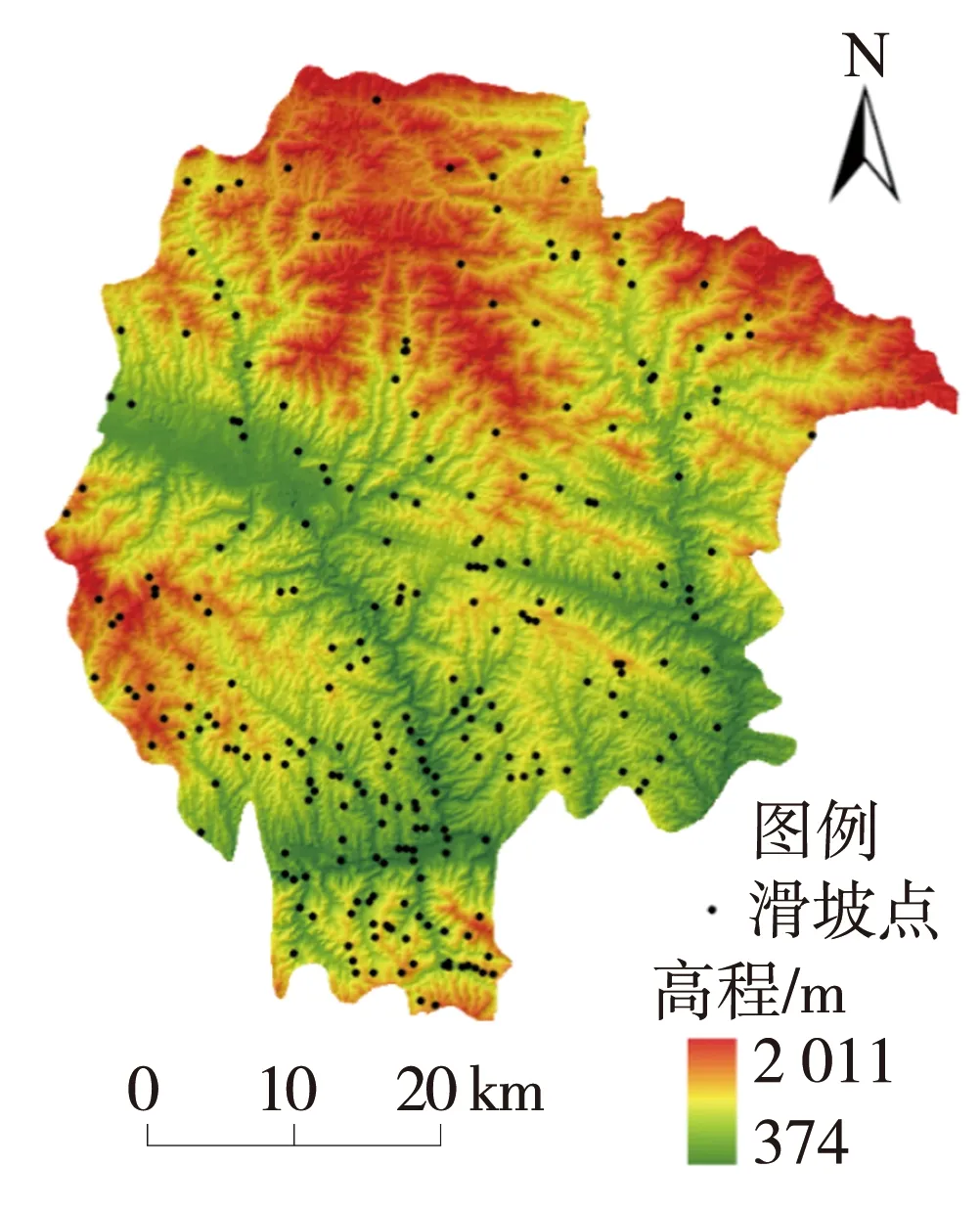
3 评价模型数据预处理
3.1 评价单元与影响因子的选取
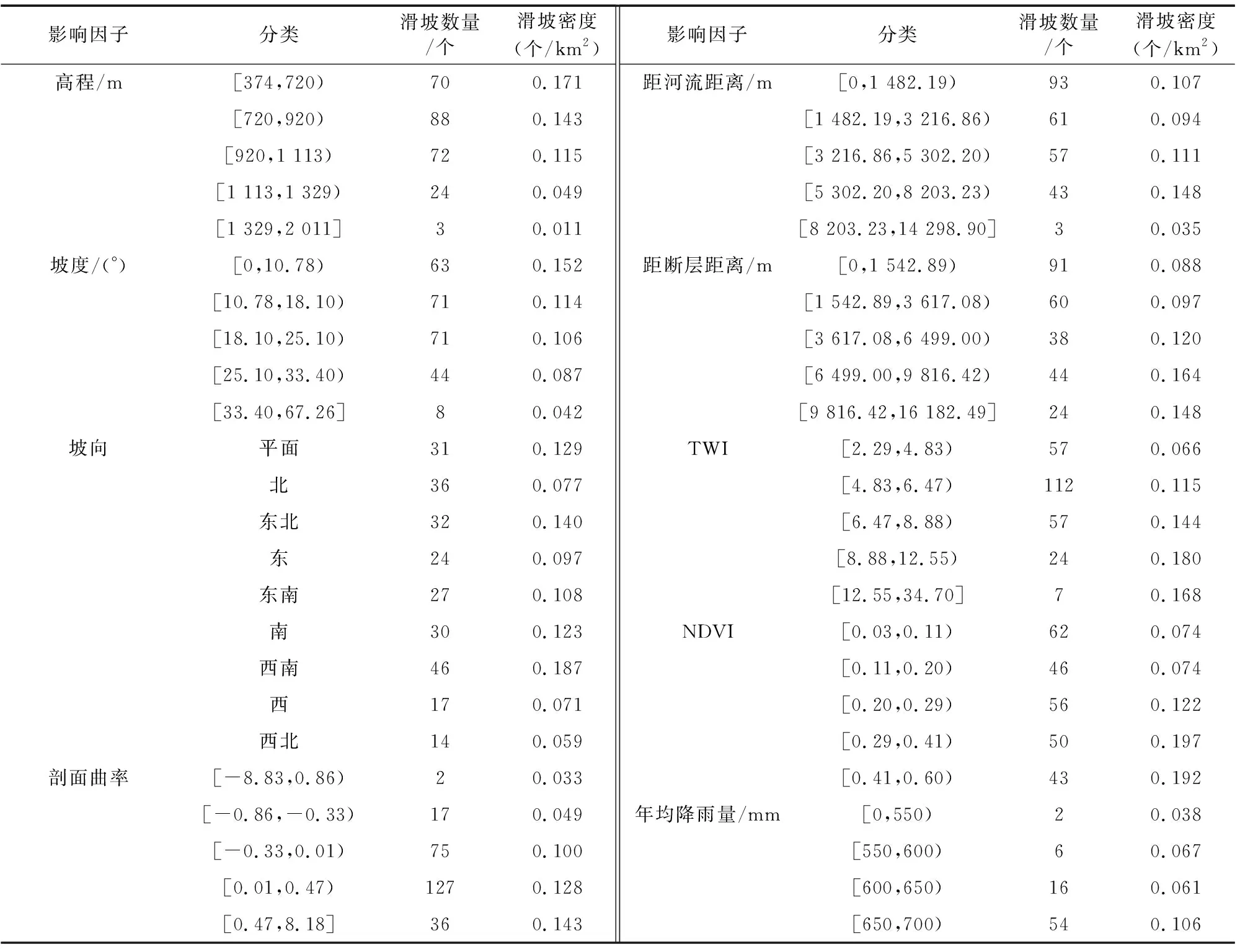
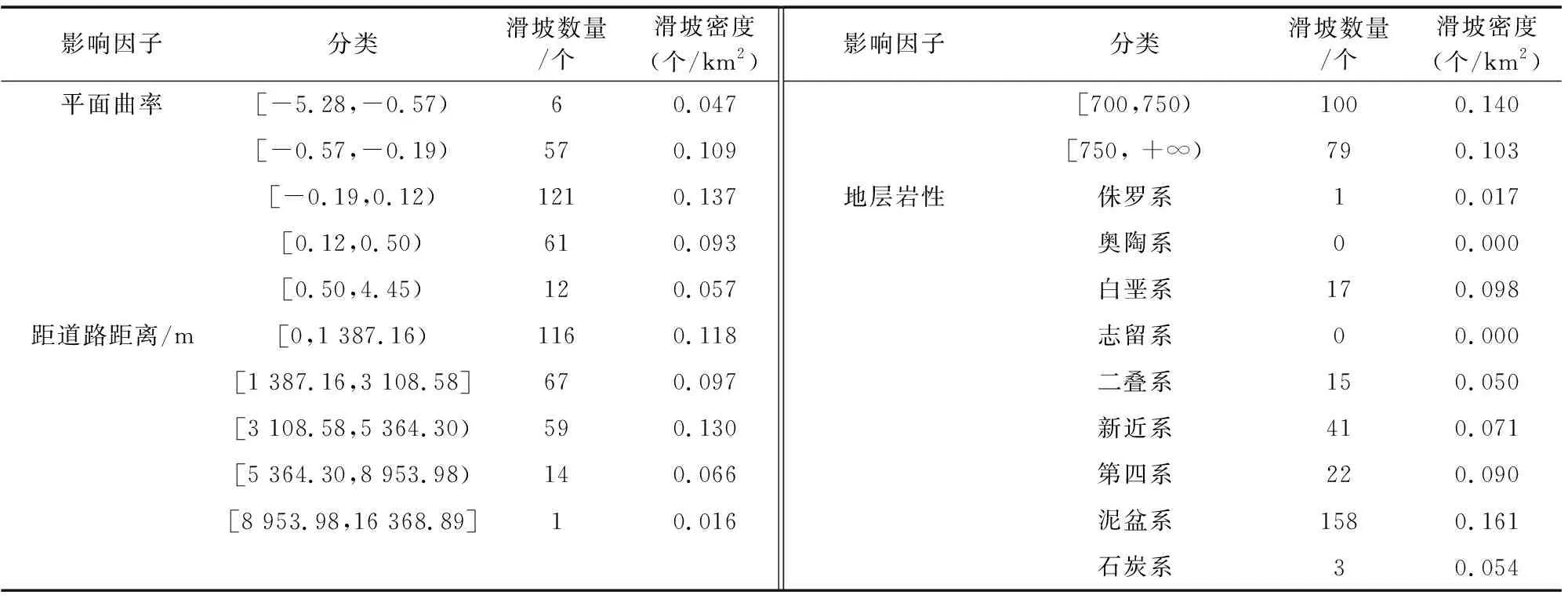
3.2 模型数据集构建
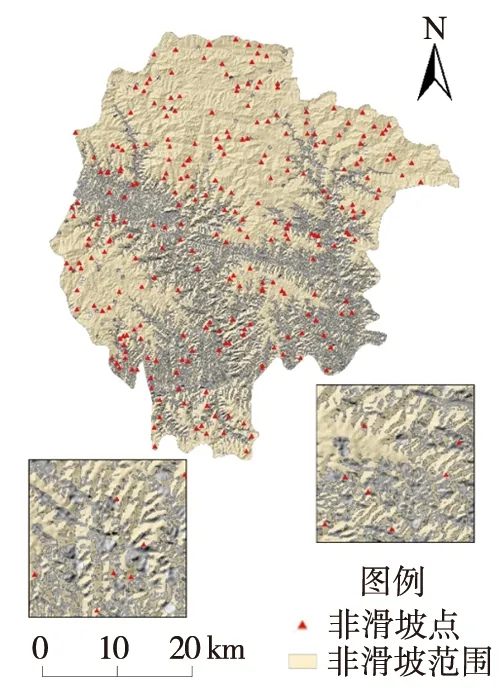
3.3 影响因子的筛选
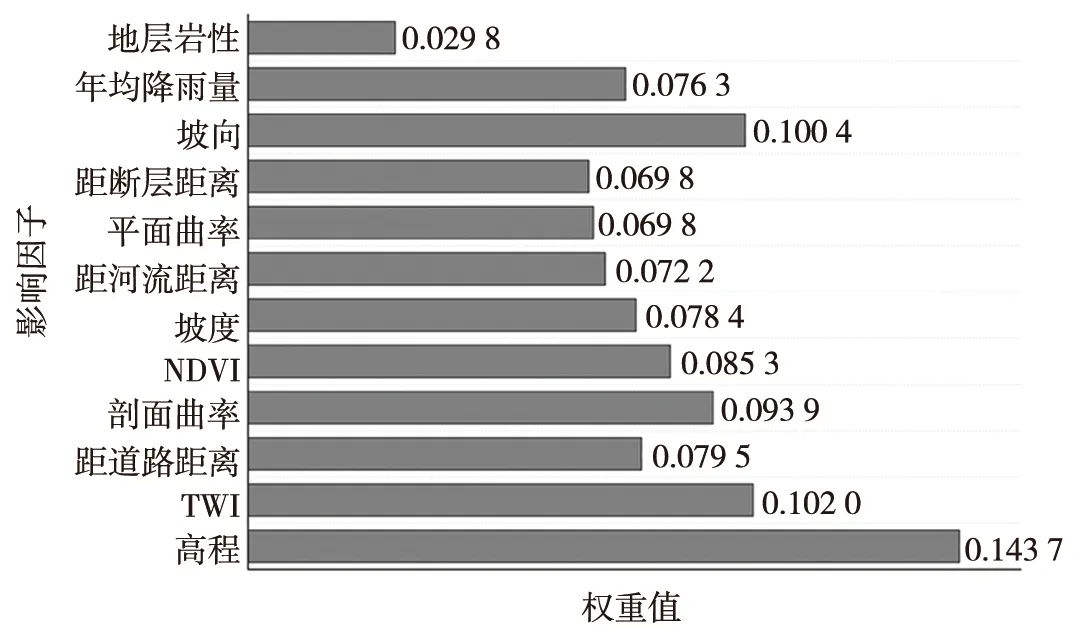
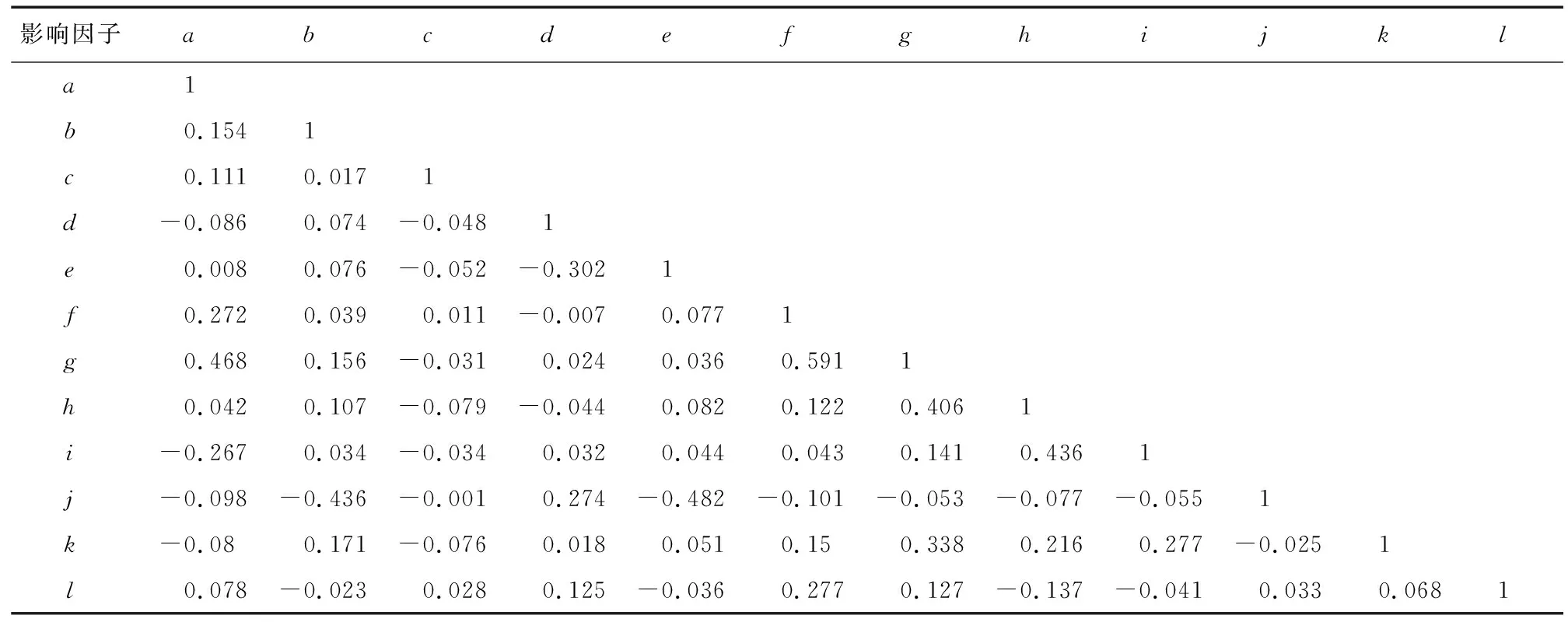
4 滑坡易发性评价
4.1 基于基分类器模型的滑坡易发性评价
4.2 基于Stacking模型的滑坡易发性评价
5 模型验证与讨论
6 结论

