地下水位抬升对黄土高填方地基增湿影响研究
朱才辉,彭 森,刘争宏,张继文
(1. 西安理工大学 岩土工程研究所,陕西 西安 710048; 2. 陕西省城市地质与地下空间工程技术研究中心,陕西 西安 710068; 3. 陕西省水工环地质调查中心,陕西 西安 710068;4. 机械工业勘察设计研究院有限公司,陕西 西安 710043)
0 引言
黄土地区沟壑纵横,城市空间狭小,严重限制了城市的发展,为此通过“深挖高填”工程来拓展城市居住空间、交通及工业建设的工程案例愈来愈多,但其存在的岩土工程问题也较为显著。其中,针对黄土地区地下水的运移模式,尤其是针对黄土高填方施工前后地下水位的变化以及可能存在的增湿变形问题、边坡稳定问题一直备受关注。
探索黄土地区的地下水来源及补给特征是确定地下水位演化规律的首要条件,以往对于黄土高原地区的长期降水入渗试验研究认为[1],由于受到较强的蒸发作用,降水难以对地下潜水进行补给,且通过土壤水中的氘氧同位素追踪试验证明,土壤水主要来自于地下水,而外源水主要源于河流、湖泊的补给,由此推断,黄土地区的地下水与直接降水关系不大,而与外源水有关,但对黄土地区梁峁沟壑状地貌单元受到人为改造后的地下水补给特征未作探讨。为此,有学者针对某黄土削峁填沟高填方工程为背景[2-4],针对填方地基在竣工前后的地下水位、孔隙水压力、土体含水率、盲沟水流量、地表水入渗情况进行了长期的监测和分析,监测结果显示:黄土沟壑区高填方施工抬高了局部区域的地下水位,短时间的降水难以对地下水进行补给,但场地内发育的裂缝易成为地表水下渗通道,提出了黄土沟壑高填方工程中沟谷地下水排导措施,为黄土沟壑区高填方工程的设计、施工提供了科学的参考。此外,有诸多学者针对地下水位变化对高填方机场、路基、工业厂区和房屋建设地基的影响方面开展了有意义的研究,机场高填方坡脚部位稳定的地下水会引起高填方地基长期沉降变形和边坡不稳定[5-6]。挖填黄土沟壑区形成的露天工业内地下水排泄受阻、地下水位上升是导致深部黄土湿陷、场地地基失效、填土高边坡失稳等问题的重要原因[7]。地下水位变化会引起建筑地基土中附加应力、承载力大幅度下降和不均匀沉降等问题[8-9]。上述工程问题均与非饱和黄土的土水特征、渗透特性、毛细现象有关[10-14],基于室内试验、模型试验和数值分析研究,认为填方压实土的渗透性大大降低(天然黄土渗透系数一般0.02~0.3 m/d,压实土渗透系数量级一般为10-4m/d[10-11],回填土渗透性低,降水渗入较困难,导水性差,使进入土体中的水也不宜排出,此外,基岩裂隙水和孔隙潜水的缓慢入渗,可能会导致土体由下而上逐渐饱和,从而引起地下水位抬升。
然而,关于黄土地区沟谷中高填方施工对地下水位的影响规律,仍存在一定的争议,有学者认为[15-16],西部黄土沟壑区地下水的补给区与径流区一致,大气降水是地下水唯一补给来源。由于沟谷深切,地形破碎,地下水接受补给的条件较差,降水多以表流形式向沟谷排泄,少部分垂直入渗补给地下水。地下水主要排泄方式是沟谷泉水,形成地表径流最终排至河谷,除此之外便是蒸发排泄和居民生活用水汲取地下水。从陕西近50 a气候及城市化的进程上讲,随着人口增多、地下水的过量开采,加之气候的变暖,降水量减少,地下水位长期呈下降趋势。随着填方造地工程的进行,进一步减少地下水的补给,地下水位会发生下降趋势。
综上可见,上述针对黄土地基中“水”的问题开展了大量原位监测、室内试验、模型试验、数值分析等研究,对深刻认识沟壑区高填方施工前后的原地基及填方地基内部地下水的变异特性具有重要的科学和工程意义,但对于黄土沟壑区水位抬升对高填方地基增湿影响问题研究尚不够,文中试图通过已有的某黄土高填方地基内部水分场原位监测结果,结合室内试验和模型试验来分析地下水对压实黄土的增湿规律,并基于数值分析方法,来分析某黄土高填方地基在水位抬升情况下的入渗增湿特性和增湿变形规律,以期通过文中的研究,为类似黄土沟壑区高填方地基设计提供科学参考。
1 工程背景及岩土工程问题
1.1 高填方工程背景
以陕北某黄土高填方工程为背景[2-4],该试验场区地层可分为梁、峁、冲沟等主要地形地貌,梁峁顶面宽度50~150 m,坡度一般小于20°,下部坡度一般30°~40°,坡高一般100~150 m。梁峁区主要地层为Q3黄土(厚10~20 m不等,局部可达30 m以上)、红黏土和砂岩、泥岩;冲沟区地层与梁峁区黄土地层厚度有所不同,但分布有第四系全新统地层,在风化泥砂岩地层中蕴藏孔隙潜水和基岩裂隙潜水,其中孔隙潜水渗透系数一般为0.014~0.023 m/d,且沟谷中的地下水埋藏脚浅,为1.5~9.7 m,含水层厚度约为2.3~8.6 m;而风化基岩裂隙潜水,渗透系数0.022~0.471 m/d,水位埋深为地表以下16~36 m,厚度约20~40 m。该地区7—10月份的连续阴雨有利于水分向深层渗入,从而引起一部分黄土含水量增大,一部分水分在重力作用下沿着黄土中的孔隙裂隙逐渐下渗,在红黏土或泥岩的隔水层表面形成上层滞水,然后以下降泉的形式排泄于沟谷中,冬季出现冻结成冰,见图1,次年春季下降泉逐渐消失,表明上层滞水排泄完毕。

图1 沟谷底部下降泉出露Fig. 1 Springs fall from the bottom of the gully
本试验段施工控制方法如下:填方体设计采用的重型击实试验标准,取压实度为0.90~0.95,平均为0.93,填料的含水率控制在最优含水率±2%,填方施工前期,采用振动碾压方法原地基压实;大面积施工后,采用冲击碾压进行压实填方体。对填挖交界处、工作面交接处、基岩出露处、黄土陡坎间的狭窄区域等采用点夯强夯法处理。为了减少地下水位对高填方地基增湿影响,沟谷采用盲水盲沟和涵管形式排水。
1.2 高填方深层地基增湿问题
以该黄土高填方试验段某沟谷中断面的实测数据为例进行分析[2-4],该典型断面填方及原地基中布置了1#、2#、3#这3个含水率观测孔,监测断面的布置示意图见图2。
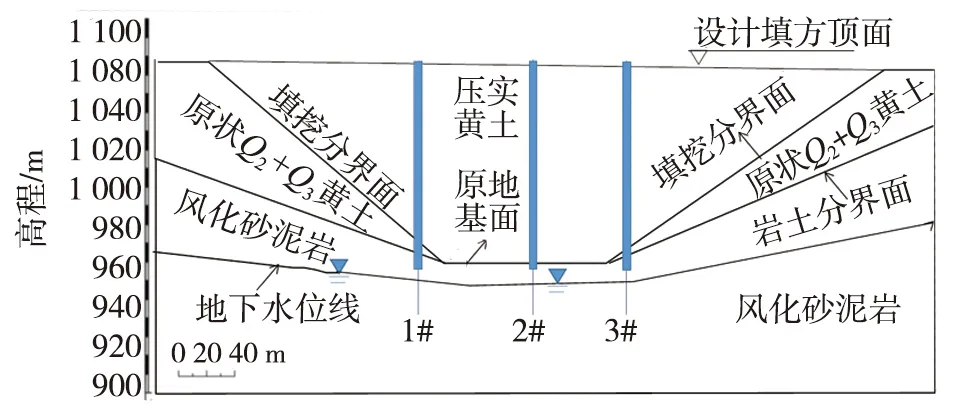
图2 某高填方地基典型监测断面Fig. 2 Monitoring section of a high-fill foundation
本次采用的含水率观测孔为人为挖掘监测孔,孔径约为75 cm,无套管。含水率观测孔探头布置方式如下:地下水位面至原地基面以上9 m范围内,竖向距离每间隔3 m设置一个土壤水分计TDR探头,用于监测地下水位上升;填筑体顶面以下7 m的深度范围内每隔5 m布设一个TDR(time-domain reflectometer,TDR)探头,用于监测地表水入渗;在填挖交接面处设置1个TDR型土壤水分计,用于监测交界处裂缝水分入渗情况。布置现场见图3。

图3 TDR监测点布设Fig. 3 Layout of monitoring points with TDR method
从填方顶部至原地基在不同高程处的含水率在竣工前后的变化趋势见图4。可得如下结论:
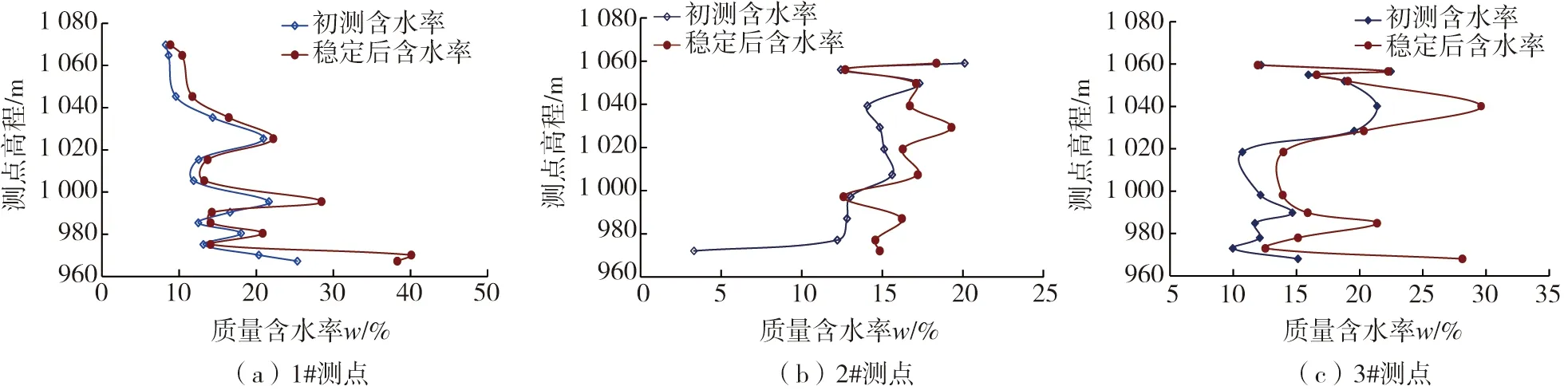
图4 不同监测点处高填方地基含水率随深度分布Fig. 4 Measured water content with depth in the HFF
1)黄土高填方在填筑压实期间采取的初始含水率基本控制在16%左右,满足设计要求,高填方地表以下约1.5 m范围内的土体含水率相对初始状态下偏低,可能填方作业后土体水分蒸发减少所致。
2)将上述高填方地基不同深度处的监测点在初始和稳定阶段的含水率加权平均值进行对比发现:1#、2#、3#测井中的初始含水率分别从15%、14%、15%增大至工后阶段的19%、16%、19%,可见,稳定后的含水率相比初始状态约有2%~4%的增量,表明填方后原地基和填筑体本身的含水率在增大,且原地基局部测点含水率的增幅最大,可高达20%,基本由初始的非饱和状态达到饱和状态。其中,填方体含水率短期内达到稳定后,填方中部位置的2#监测孔底部含水率(15%)较临近沟谷处监测孔1#、3#的含水率(30%~40%)偏小,可能原因是沟谷两侧与填方体交界面处存在如图1所示的下降泉出水口,靠近该部位的监测点与“水源”更接近,水分向1#、3#监测孔周围填方体的迁移效应更为明显所致。
3)分析高填方地基中水分增加的可能原因是:①随着填土荷载的增大,填筑体逐渐压密,而压实黄土的渗透性和导水性均较差,水分难以排出,从而引起上层水分向原地基底部聚集,导致含水率上升;②原地基岩体中的裂隙水和孔隙潜水在大面积填方荷载压缩作用下产生超孔隙水压力,导致裂隙水向填方内入渗;③非饱和压实黄土的基质吸力作用,诱使基岩裂隙水向填方地基内缓慢迁移,从而可能接受裂隙水补给。
4)文献[2-4]中提到的后期下游沟谷中水位监测中,表明地下水位略有3 m左右的上升,然而对于抬升引起的增湿范围及增湿变形未进行深入分析。
如前所述,原本可以自由排出的裂隙水,当受到沟谷中填方土体的封堵,可能会在填方底部产生聚集,此外,考虑到排水措施可能失效,从而诱发沟谷底部填方土体的水位抬升,最终诱发高填方地基出现增湿变形和不稳定问题,上述问题均与黄土的水敏性、渗透性、非饱和特性有关,有必要针对原状或压实黄土的土水特征曲线、渗透系数、增湿后强度、刚度软化特征开展实验研究。
2 黄土增湿特性试验研究
选取陕北某黄土高填方场区Q3和Q2黄土进行室内常规物理指标试验,取土深度为地表以下5.5~6.0 m,轻型击实试验得到填方中填料Q3黄土最优含水率wop=16%,最大密度为1.77 g/cm3,物理指标见表1。

表1 Q3和Q2黄土的主要物理指标Table 1 Physical parameters of Q3 and Q2 loess
2.1 土-水特征曲线及渗透性试验
采用常规压缩固结仪和GCTS(geotechnical consulting &testing systems, GCTS)土水特征曲线仪等系列设备进行脱湿非饱和土水特征曲线试验,当考虑固结压力对重塑黄土的非饱和特性影响时,先将不同压实度下的黄土试样再不同固结压力σ(25~2 000 kPa)下进行饱和状态下固结压缩实验,当竖向应变低于规范值后,迅速取出固结试样置于GCTS土水特征曲线仪中进行脱湿试验,同时对不同试样进行饱和渗透试验。本次试验中采取的重塑Q3黄土压实度分别为0.88、0.90、0.93、0.95、0.98。现以σ=200 kPa下不同压实度Q3黄土及原状Q3、Q2黄土的SWCC试验结果见图5(a),压实度为k=0.90时的Q3黄土SWCC曲线见图5(b)。不同干密度下原状Q3和Q2黄土的饱和渗透系数见图6。
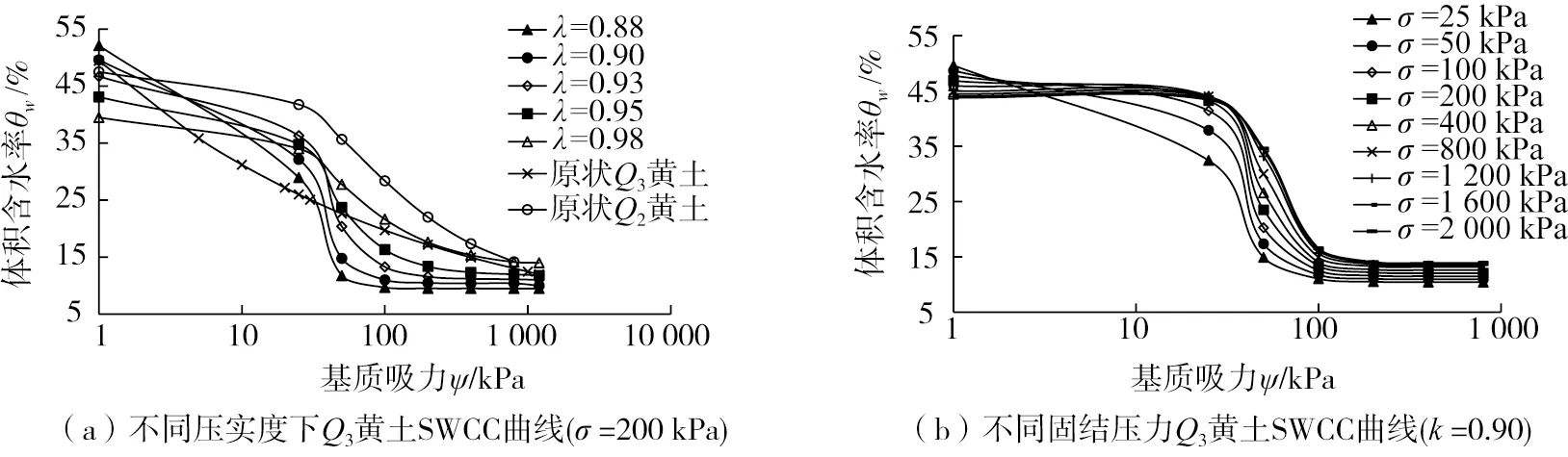
图5 压实黄土的土-水特征试验Fig. 5 Soil water characteristics of loess
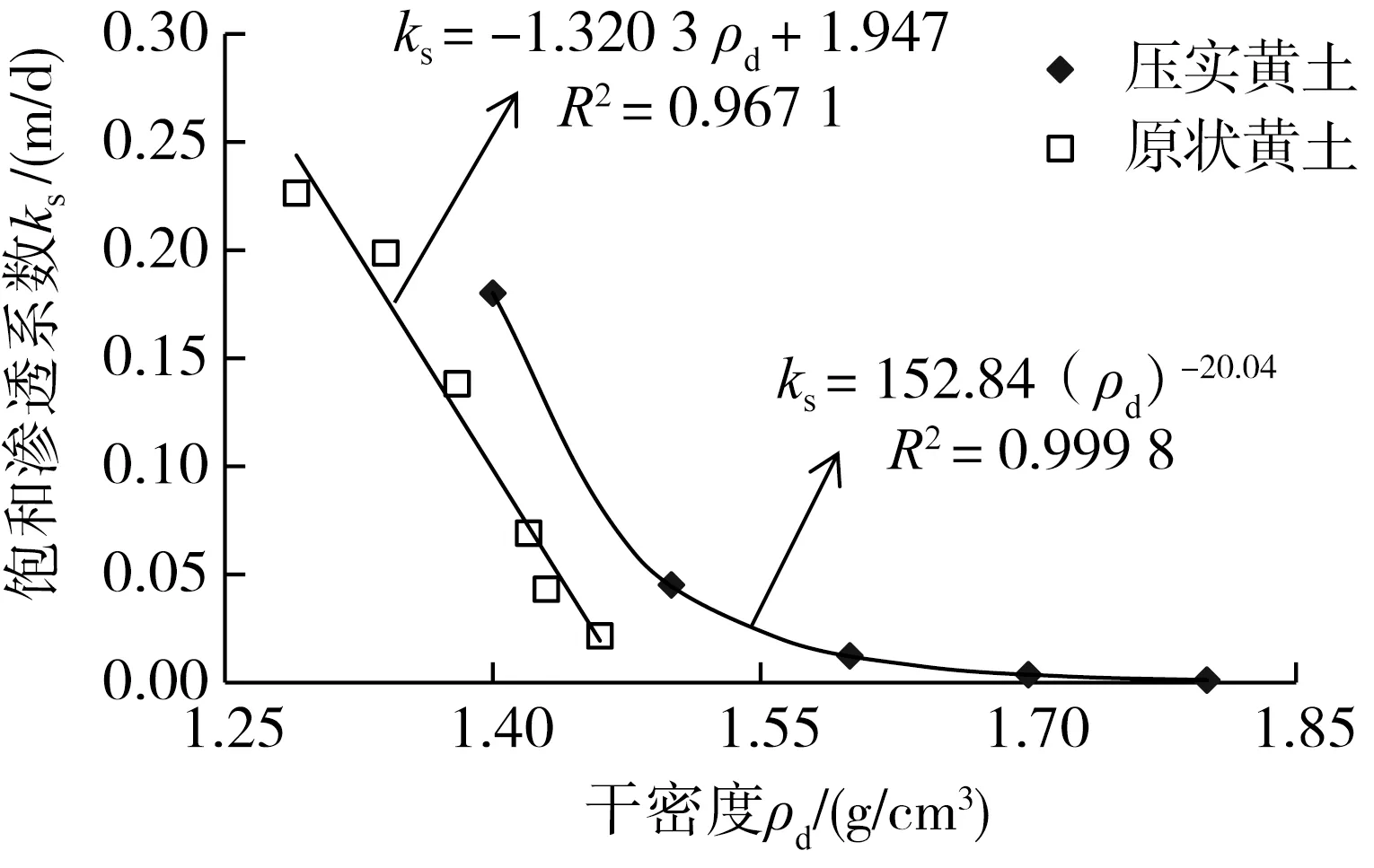
图6 压实及原状黄土饱和渗透系数与干密度关系Fig. 6 Relationship between saturated permeability coefficient and dry density of compacted and undisturbed loess
大量研究表明,黄土的SWCC曲线采用Van Genuchten[17-18](简称V-G模型)方程来描述较为合理,
(1)
式中:θs为饱和体积含水率;θr为残余体积含水率;ks为饱和渗透系数;a(kPa-1)、m、n为V-G模型参数;ψ为基质吸力(kPa)。
基于式(1)采用最小二乘法进行曲线拟合,可得到压实黄土和原状黄土的V-G模型参数见表2,由上述试验结果表明:
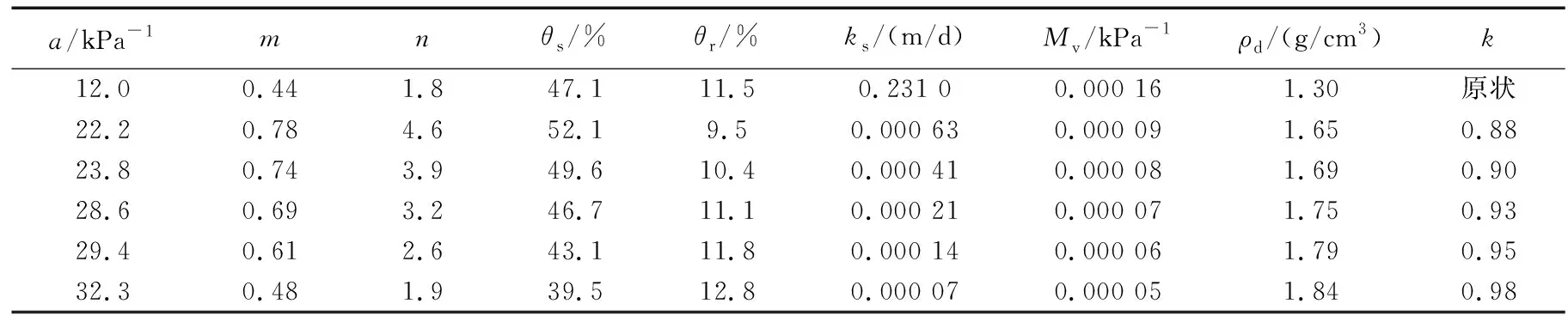
表2 不同压实度(干密度)下Q3黄土V-G模型参数Table 2 V-G model parameters of Q3 loess under different compaction degree (dry density)
1)由图5可知,随着压实度和固结压力的增大,土水特征曲线坡度越缓,其V-G模型参数中,a=12~32.3 kPa-1,m=0.44~0.78,且随着干密度的增大而增大;
2)由图6可知,饱和渗透系数随着干密度增大而逐渐减小,原状黄土(ks=0.02~0.25 m/d)的饱和渗透系数约为压实黄土(ks=n×10-4m/d)的103倍。其中压实黄土的渗透系数与干密度呈幂函数关系,原状黄土的渗透系数与干密度呈线性递减函数关系。
2.2 压实黄土软化特性试验研究
开展不同压实度下Q3黄土在不同含水率下的固结压缩试验和抗剪强度试验, 得到不同含水率下的土体的压缩模量Es、黏聚力c、内摩擦角φ等参数的变化规律,如图7所示。压缩模量Es(MPa),黏聚力c(kPa)、内摩擦角φ(°)等参数与体积含水率θw之间的函数关系如表3所示。从图7及表3可见,在相同的压实度情况下,土体的压缩模量Es随含水率的增大均呈对数函数减小趋势,黏聚力c和内摩擦角φ随含水率的增大呈线性减小趋势;同一含水率条件下,压实度越大其压缩模量Es、抗剪强度指标c和φ越大。

表3 不同压实度下Q3黄土V-G模型参数Table 3 V-G model parameters of Q3 loess under different compaction degree
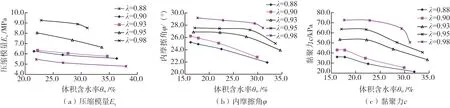
图7 压实Q3黄土力学参数随含水率变化规律Fig. 7 Variation regularity of mechanical parameters with moisture content of compacted Q3 loess
3 地下水位抬升对地基增湿影响
3.1 水位抬升对高填方地基水分场影响
上述针对某高填方地基水分演化规律进行了监测分析,但在工程实际中仍难以通过填方沉降的监测数据来具体分离出因地基增湿引起的工后沉降分量,为此有必要针对填方地基水位抬升引起的增湿水分场分布规律及引起的增湿变形进行数值分析。根据该高填方工程实际,选取典型高填方地基断面,填方高度为H=120.0 m,沟谷坡度为40°,填方平均压实度为k=0.90,采用GeoStudio软件中的SEEP/W分析模块进行非饱和土渗流计算[21]。由于地层条件的不均匀性,本算例对图8中典型断面进行了简化,模型中土岩交界面以下约2~5 m处为初始地下水位,地下水位线处采用常水头边界,模型上边界为自由边界,模型两侧为排水边界。沟谷中黄土高填方的地下水抬升入渗有限元模型如图8所示。根据高填方沟谷模型及该区域的水文地质概况:假定地下水位相对于原始水位线的抬升高度分别为Δh=0.0(初始状态)、3.0、5.0、10.0、15.0、20.0、30.0 m等7种工况进行数值分析,模拟水位抬升期间引起地基水分场变化问题,其水位不同抬升高度下,高填方体内的水分场分布规律云图如图9所示(以Δh=0.0、30.0 m为例),不同深度处体积含水率的量值θw和含水率增量Δθw分布如图10所示。
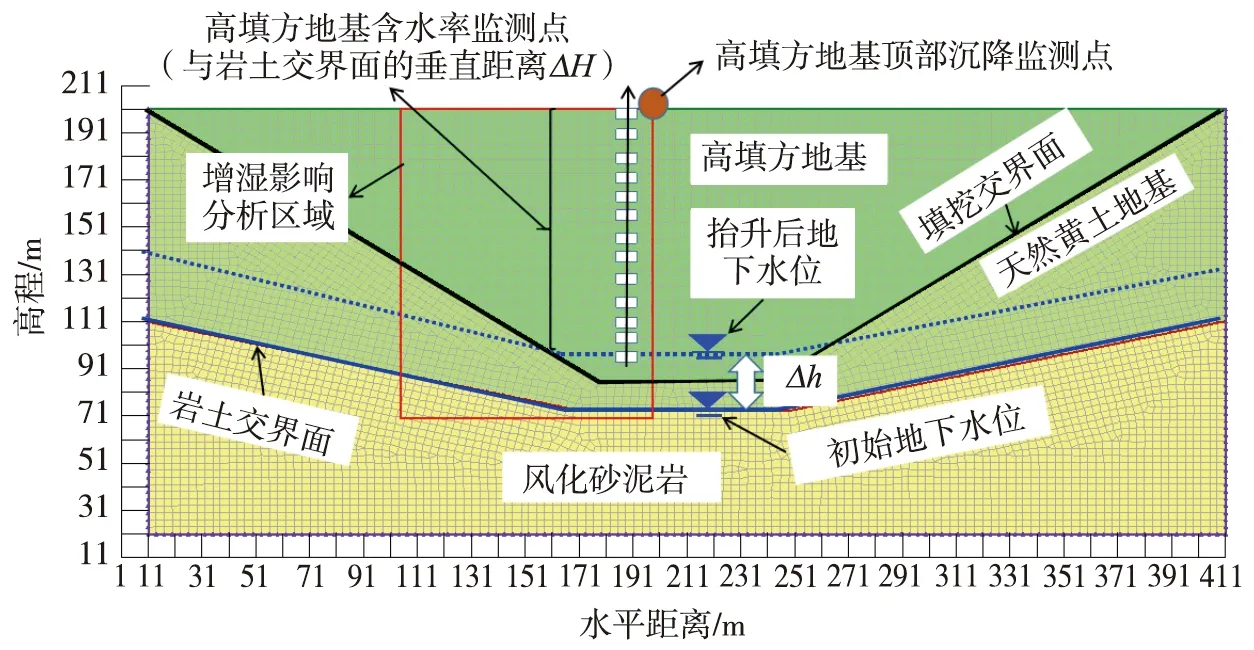
图8 高填方地基地下水位抬升有限元模型Fig. 8 Finite element model in loess high-fill embankment due to groundwater uplift
由上述非饱和渗流分析,可得到如下结论:
1)由图9(a)、(b)可知,在初始水位条件下(Δh=0.0 m)和地下水位抬升Δh=3.0 m时,水位线以上2.0 m范围内土体处于饱和状态,初始水位线以上31.0 m范围土体受到增湿影响,其含水率高于填方地基初始含水率(9%),而初始水位线以上10 m范围内土体增湿影响最为剧烈,且其增幅沿高程向上递减,可见由于非饱和压实黄土毛细吸力作用,会诱使水位线以上很大范围内的土体出现增湿现象。
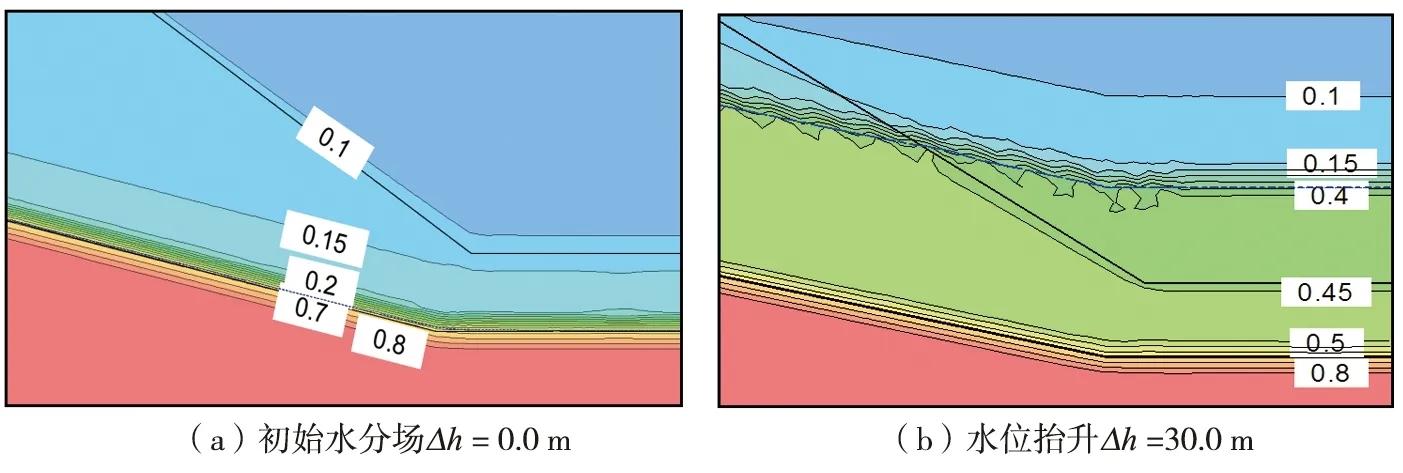
图9 地下水位抬升不同高度Δh时高填方地基含水率沿高程分布规律Fig. 9 Water content distribution along the elevation under the condition of different elevation of groundwater uplift Δh
2)由图10(a)可知,随着地下水位由Δh=3.0 m向上抬升至Δh=30.0 m的过程中,水位线以下土体基本趋于饱和,水位线以上土体的含水率呈台阶状分布,且水位线以上10.0 m范围土体的增湿影响最为剧烈,超过水位线以上10.0 m的土体增湿影响程度较小,不超过2%。可见,随着水位抬升高度的增大,水位抬升对高填方地基的增湿影响范围不容忽视。
3)由图10(b)可知,随地下水位抬升高度Δh增大,距离基岩不同高程ΔH处的含水率增量Δθw呈“S”型分布,越靠近水位线附近,土体的含水率增量Δθw越大,距离基岩(初始水位线)高度ΔH≥34 m时,含水率增量Δθw随Δh增大幅度较小,表明,水位抬升影响高度最大不超过31.0 m。
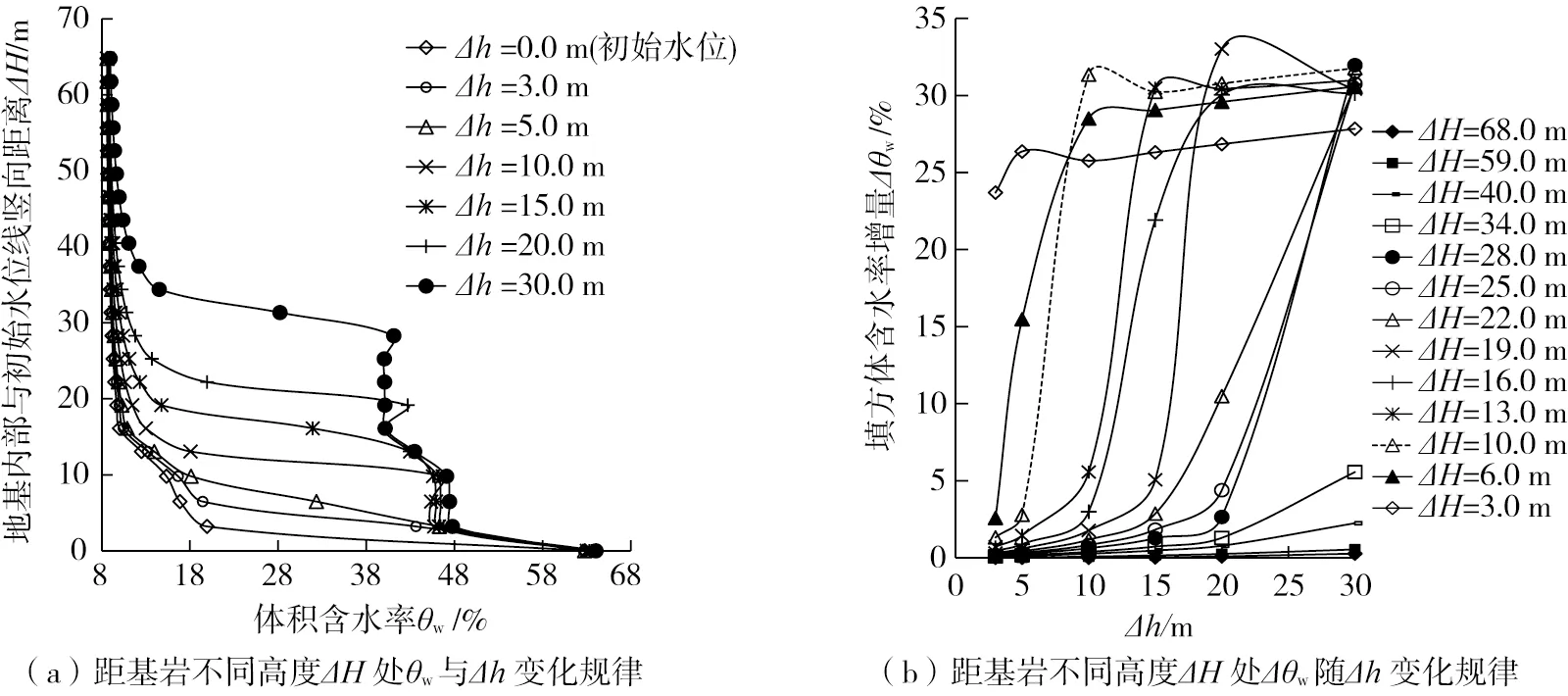
图10 高填方内部水分场与水位抬升高度关系Fig. 10 Relationship between water filed and elevation of groundwater uplift
3.2 高填方地基增湿压缩比分析
关于非饱和黄土地基的增湿变形研究较多,不同学者开展了不同初始状态下黄土在增湿前后的刚度、强度弱化函数研究[19],构建考虑各类影响因素下的非线性本构模型、弹塑性损伤流固耦合模型,并编制有限元程序来研究非饱和黄土的湿化变形,最终应用于填方地基在增湿条件下湿化变形和边坡稳定性计算[20-24]。概括起来,增湿变形的计算方法主要包括:全耦合法和等效法。全耦合方法基于“土-水”互溃作用机理来探索非饱和黄土的增湿变形问题,但实际操作难度较大[25];等效方法是构建物理状态演化与力学参数之间的对应关系来描述土体增湿变形问题,该方法较为简单。笔者拟采用等效方法思路进行增湿变形计算:
1)假定风化砂泥岩含水率的增大不引起地基沉降,仅选取风化砂泥以上的原地基土层和填方压实黄土层的增湿单元进行数值分析。
2)计算初始水位条件下的水分场,根据表2、表3中的参数表赋予其在初始渗流场(水分场θw1)、应力场下的物理力学参数,然后采用摩尔-库伦模型计算其初始水分场下高填方地基的应力-应变场,得到其初始水分场下的自重位移场S1(见图11)。
3)根据研究方案中地下水位抬升高度Δh,修改地下水位边界条件,重新计算水位上升某一高度Δh的渗流场(水分场θw2),计算增湿区域所有有限单元的水分场增量Δθw=θw2-θw1,提取Δθw≥0的单元,根据表3中不同含水率条件下的土体物理力学参数的拟合公式,重新给增湿后的单元赋予新的物理力学参数,计算增湿后的高填方地基应力-应变场,得到其增湿后自重位移场S2(见图12)。
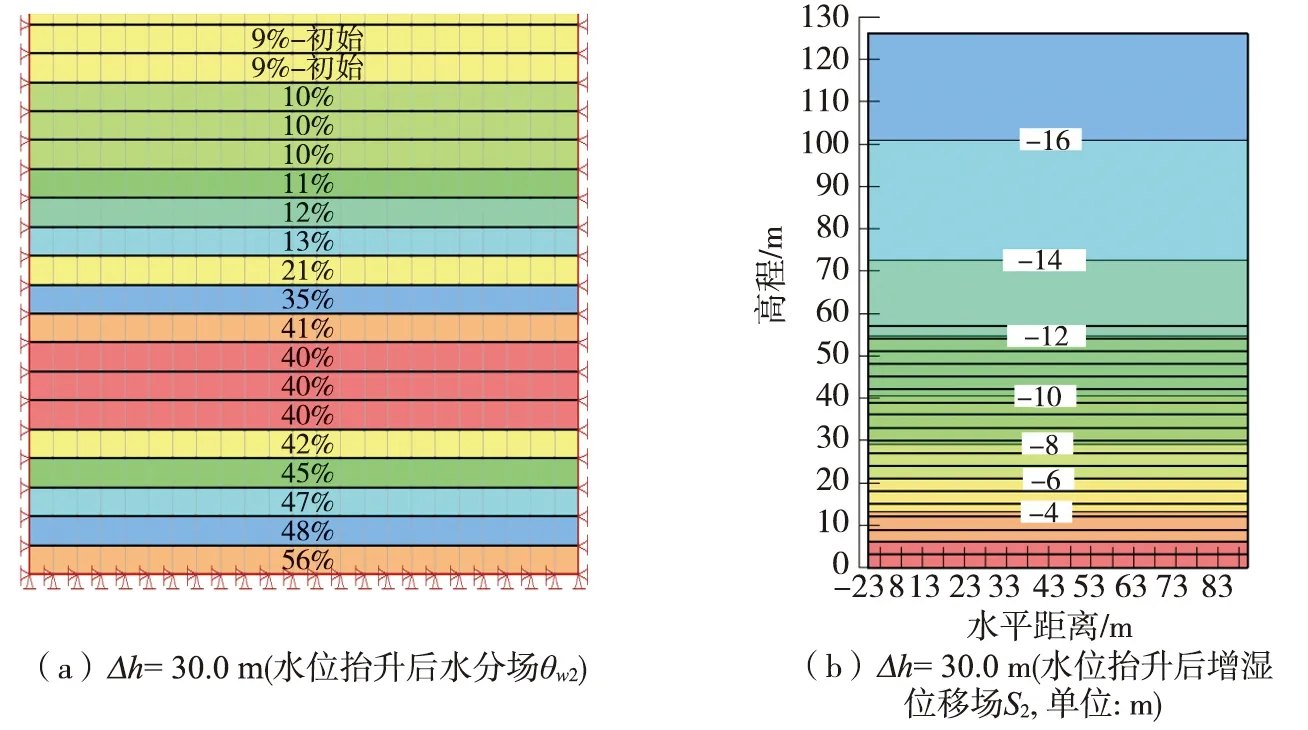
图12 Δh=30.0 m时 θw1分布规律及竖向位移场S1Fig. 12 Distribution regularity of θw1 and S1 under Δh=30.0 m
4)将增湿后计算得到的位移场S2减去增湿前的位移场S1,即可得到增湿变形场ΔS=S2-S1,产生的差值ΔS作为水位抬升引起的增湿变形场。
为了得到高填方地基在地下水位抬升条件下的增湿压缩变形规律,现定义增湿压缩比β,如式(2)所示:
(2)
式中:参数β为高填方地基在增湿后引起的增湿沉降ΔS与填方地基的总高度H之间的函数关系,代表了单位厚度填方产生的增湿压缩应变。
根据上述步骤2)—4)来计算增湿变形,得到高填方顶部的累积沉降,如图13所示。
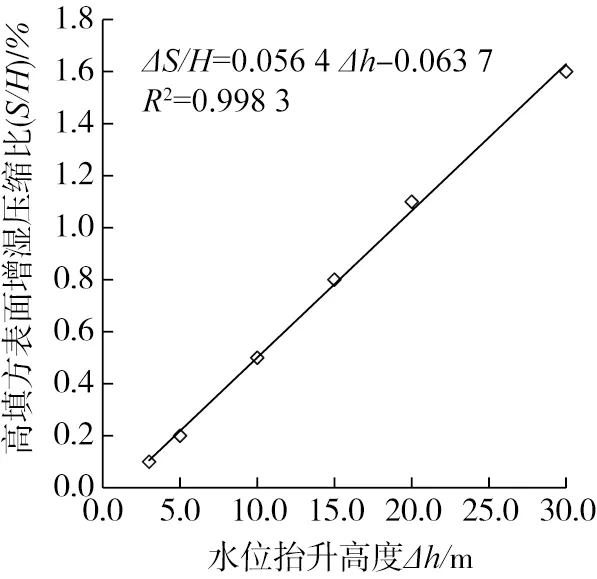
图13 水位抬升高度Δh与高填方地表增湿压缩比β之间的关系Fig. 13 Relationship between the wetting compression ratio (β) and the elevation of groundwater uplift (Δh) of loess high-fill embankment
从上述分析结果可得到如下结论和建议:
1)随着地下水位抬升高度Δh的增大,引起高填方地基表面的增湿沉压缩比β呈线性增大趋势,当地下水位线从Δh=3.0 m抬升至Δh=30.0 m期间,高填方地基增湿压缩比从0.14%增加至1.61%,采用式(3)来预估增湿引起的高填方顶部沉降(适用于填方平均压实度为k=0.90,含水率为最优含水率的情形):
β=0.056 4Δh-0.063 7
(3)
2)根据式(3)可推算,当地下水位线抬升Δh=3.0 m后,填方高度为H=120.0 m的黄土高填方地表发生了约平均ΔS=170 mm的增湿沉降,当地下水位抬升至原水位线以上Δh=30.0 m后,高填方地表增湿沉降高达ΔS=1 936 mm,可见原地基中地下水位的抬升将对高填方的后期增湿变形产生较大影响,因此,在高填方工程的原地基与填挖交界面处应设置永久性的防排水和隔水措施,并应考虑防排水效能及可能会失效的应急排水及地基加固措施。
3)根据上述分析结果可推测,当地下水位抬升不同高度Δh时,黄土高填方地基底部的增湿变形对填方顶部将产生较大的差异沉降。由于高填方地基水循环达到新的平衡需要较长时间,短期内黄土高填方区顶部不适宜布置建筑物,至于合理布置建筑物的时间,需要结合高填方地基中地下水位变化特征、水分场迁移特征、地表水入渗程度、地表径流产流特征及填方地基工程所在区域采取的防排水措施效能发挥程度来综合确定,文中所探讨的只是高填方地基增湿后变形达到稳定的瞬态分析状态,对于更深层次的分析建筑物施建时间,将是下一步的重要研究工作。对于短期内需要在填方地基上部进行修筑建筑物时,有必要采取适当的结构加强措施和对填方地基采取进一步的处理措施,初步建议如下:①在沟谷状高填方地基的沉降盆中部,沉降量较大但相对均匀,可考虑为中高层建筑地基,对沉降量要求较高的区域,适当考虑摩擦型承台群桩基础及其他整体性较强的刚性基础,或采取适当的地基加固措施,如基于SDDC工法的碎石桩、灰土桩等;②在沉降盆侧翼或填挖交界处的差异沉降较大区域,不建议作为建筑物天然地基,如平面上必须布置建筑物,建议布置重要性等级较低的建筑物,应在填挖交界附近区域采取地基加固措施,并在建筑物基础设置变形缝、沉降缝,并考虑建筑物的形体上变化;③挖方区域可作为建筑物的天然地基,但需要结合建筑物形式及地基承载力要求,适当采取加固措施。
4 结论
以某黄土高填方地基工程为例,基于实测资料分析、室内试验及数值分析方法,探讨了黄土高填方地基中含水率上升的原因,得到了不同初始状态下非饱和Q3黄土在增湿条件下的土水特征曲线、渗透性及强度软化函数,量化分析了地下水位抬升对高填方地基的水分场和增湿变形的影响规律,得到结论如下:
1)沟谷底部黄土高填方地基的含水率在短期内呈增大趋势,含水率的增幅与土体的初始含水率和压实度有关,随时间的延长,高填方地基内部地下水将运移会形成新的平衡。
2)随着非饱和压实黄土干密度和固结压力的增大,土水特征曲线坡度越缓,其饱和渗透系数越小,渗透性越低,是原状黄土的10-3倍,其抗剪强度和压缩指标随着体积含水率增加呈非线性减小趋势。
3)地下水位线从初始位置抬升至30.0 m的过程中,水位线以上约10.0 m范围内土体有剧烈增湿现象,其增湿影响高度范围最大可达30.0 m,高填方增湿沉降压缩比β与水位抬升高度Δh呈线性增长关系,地下水位从Δh=3.0 m抬升至Δh=30.0 m期间,高填方地基增湿压缩比从0.14%增加至1.61%。
4)文中的高填方地基填料对象为陕北地区Q3压实黄土,对于不同填料(其他地区的Q3、Q2黄土或Q3、Q2混合填料)在不同压实控制标准下的高填方地基因水位抬升引起的增湿变形研究及高填方地基上部建筑施建时间控制将是下一阶段的重要工作。

