降雨入渗条件下双层非饱和土边坡渐进性破坏数值分析

洪心怡,刘志强,胡春洋,熊勇林

(宁波大学 土木工程与地理环境学院,浙江 宁波 315211)

0 引言

降雨入渗是引发边坡失稳破坏的常见诱因[1-2]。而在自然界中,边坡土体多处于非饱和状态。因此,开展非饱和土坡在降雨条件下渗透变形破坏的研究,对指导边坡防护工作具有重要意义。

目前,针对边坡在降雨入渗下的破坏问题,主要通过实验与数值计算这2类方法进行研究[3-10]。实验大致可分为2类,即探究不同初始条件,如不同坡脚、初始含水量和降雨强度等与边坡稳定性之间的关系(如李焕强等[4]、王福恒等[5])和探究降雨入渗作用下边坡性质的变化和形成机制(如张磊等[3]、王维早等[6]),非饱和土坡受到雨水渗入后,其整个坡体内部的变化很难通过实验来予以详细地展示。数值计算由于其具有适应性强、精度高、可重复等优点受到学者们的广泛应用。刘子振等[7]通过不同的数值计算方法求得临界平衡状态下滑体条块的相互作用力系数和非饱和边坡安全系数,平扬等[8]对降雨入渗条件下的膨胀土边坡稳定性进行了分析。汪洋等[9]研究了小降雨入渗的非饱和土边坡稳定性计算方法,荣冠等[10]编写了非饱和渗流程序分析降雨入渗机理和模拟方法,张社荣等[11]研究了多层岩质边坡在岩层倾角、边坡坡角、结构面间距不同时的破坏机制。石振明等[12]通过改进Green-Amp入渗模型和强度折减法来分析多层非饱和土边坡的稳定性计算。谢秀栋等[13]通过编制使用程序计算相应的可靠指标,对边坡工程的整体稳定可靠度进行分析。陈勇等[14]根据非饱和土Barcelona模型进行了三维有限元数值模拟,得出非饱和土边坡的应力位移分布。宗振邦等[15]采用随机场-贝叶斯方法校准了关键岩土参数并对边坡稳定性的可靠度进行了分析。但是,以上研究对象皆为单一均质土边坡,对于多层坡体的数值分析则相对较少。受自然环境中降雨、岩石风化、动植物活动等因素的影响,土体通常在同一断面出现分层现象。不同土层之间,其力学参数以及饱和渗透系数均会发生变化。而且目前为止,大部分的研究成果都是基于极限平衡法或强度折减法来分析边坡的稳定性,没有对其进行瞬时渗流-变形耦合分析。

因此,本研究基于多相混合体理论,推导得到土-水-气三相耦合控制方程组[16-17],同时结合ZHANG等[18]提出的非饱和土弹塑性本构模型,采用有限元与有限差分法进行空间时间离散化,最终得到土-水-气三相耦合有限元控制方程,并利用Fortran90语言编制成计算程序。以KITAMURA等[19]开展的2层不同湿密度的非饱和砂土边坡模型实验为研究对象,使用计算程序对不同降雨强度与坡角的4个工况进行数值模拟分析,验证了文中所提方法数值分析方法的可靠性及实用性。

1 土-水-气三耦合有限元控制方程

1.1 控制方程

土-水-气三相耦合控制方程分为3个部分:第1部分是混合体平衡方程式;第2部分是土-水连续方程式;第3部分是土-气连续方程式。3个方程式是基于土-水-气各相的动量守恒定律和质量守恒定律推导而得[16-17]:

1)平衡方程式:

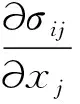
(1)

2)土-水连续方程式:

(2)

3)土-气连续方程式:

(3)

式中:σjj与εii分别为应力张量和应变张量;ρ为土体密度;bi为体积力张量;n为孔隙率;pw为水压;pa为气压;Sr为饱和度;k为渗透系数;K为体积模量;γ为重度; 上标s、w、a分别为固液体和气体。

1.2 控制方程空间/时间离散化

将上节的平衡方程式、土-水和土-气连续方程式进行空间和时间离散化后,即可得到土-水-气三相耦合有限元方程。平衡方程是基于有限元法进行空间离散,而连续方程是基于有限差分法而完成的。

首先将平衡方程进行空间离散化,基于虚位移原理,并进行一系列的计算,可得平衡方程增量的弱形式:

(4)

文中采用ZHANG等[18]提出的以Bishop有效应力和饱和度作为状态变量的非饱和土弹塑性本构模型。该模型在饱和修正剑桥模型的基础上,通过添加饱和度对土体孔隙比的影响规律而建立,模型可以自由连续地同时描述饱和土和非饱和土的力学性质。其应力增量有限元表达式如式(5):

Δσ′=DepBΔuN-ERFSΔSr

(5)

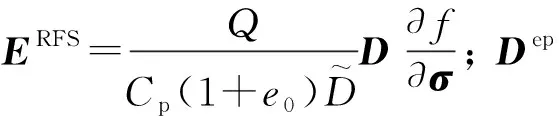
将式(5)代入到式(4)中,得到如式(6):

(6)

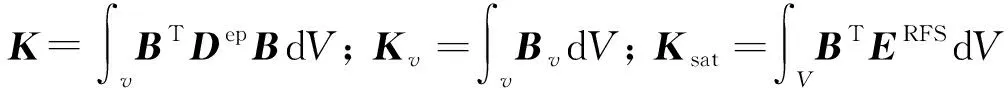
众所周知,非饱和土的饱和度与其基质吸力之间有一定的关系,文中所采用的土-水特征曲线为ZHANG等[18]提出的能够同时考虑干、湿循环效应的土-水特征曲线(soil water characteristic curve, SWCC)。基质吸力增量与饱和度的关系如式(7):

(7)

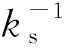
(8)

(9)

将式(6)～式(9)进行时间离散化,并计算得到平衡方程时间和空间离散化后的方程式:

(10)

将土-水和土-气连续方程式进行时间和空间离散化,得到如式(11)、式(12)所示:

(11)

(12)

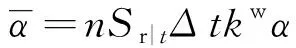
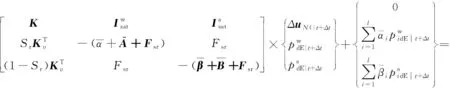
(13)

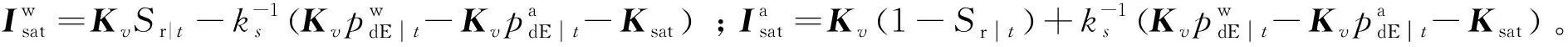
2 边坡模型的数值计算

2.1 计算模型及其初始条件的确定

KITAMURA等[19]为了探究降雨强度和双层边坡坡角对非饱和土双层边坡的破坏影响,设计了如下实验方案:首先选取日本常见的Shirasu砂土,制作了2种不同尺寸的边坡模型,模型是由2种不同湿密度的土组成。将右侧的土体记为A层,左侧的土体记为B层。2种边坡模型的实际尺寸以及孔压计布设具体位置如图1所示,并对每种边坡模型A层顶部分别进行降雨强度为50、100 mm/h的散水实验。在实验的过程中,一直保持降雨状态直至边坡发生破坏,其余实验条件皆相同。表1列出了4种工况的实验条件。

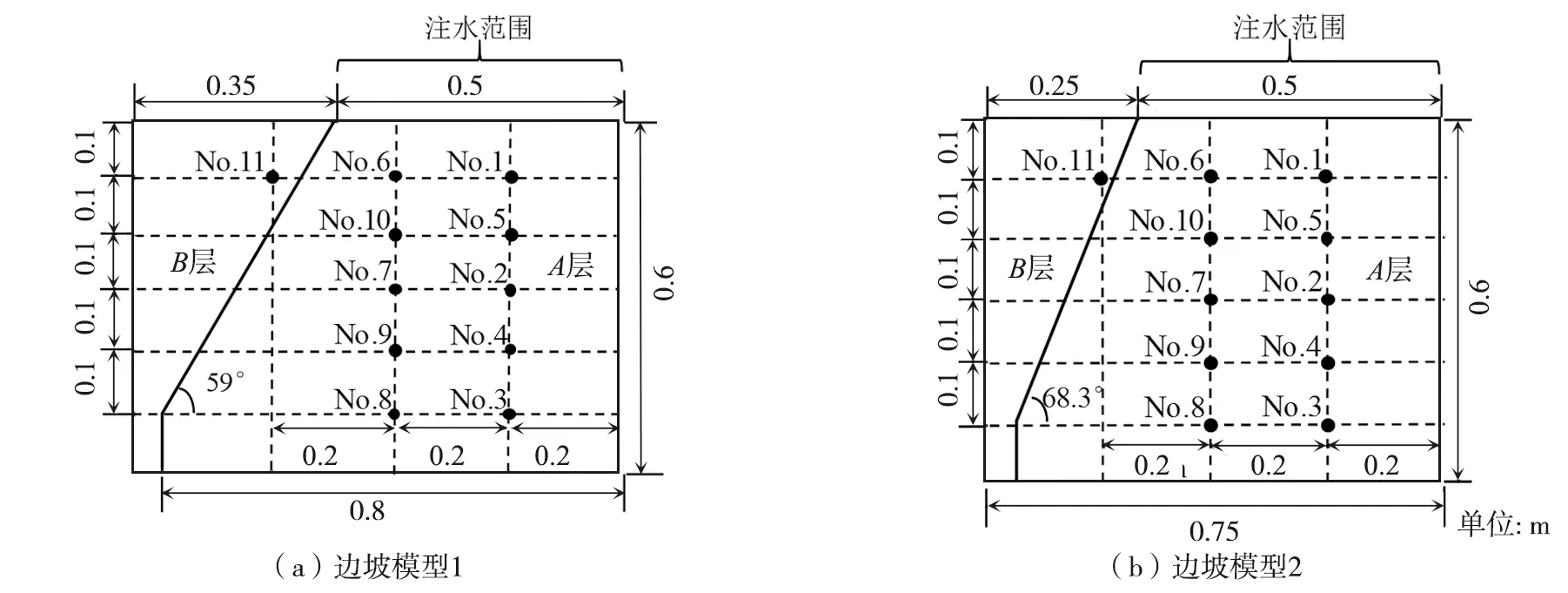
图1 实验模型的尺寸及孔压计的分布位置图Fig. 1 Size of the experimental model and the distribution position of the pore pressure gauge

表1 各工况的实验条件对比表Table 1 Comparison of experimental conditions of various working conditions mm/h

文中选此实验进行数值分析。图2反映了数值计算所使用的2个模型在二维平面内有限元网格的划分以及边界条件。2种不同尺寸的计算模型都划分成1 500个单元,模型的底部固定,右侧横向约束,其余各边自由。模型的上部,左侧以及下部为排气排水面,右侧为不排水不排气面。表2列出了实验所用A、B这2层砂土的物理特性参数。从图3可知非饱和度状态变量ρs的计算方法,即通过在参考应力pr时非饱和土和饱和土的孔隙比之差求得。表3列出了计算时所用的非饱和土本构模型的材料参数。计算模型的初始应力场通过2方面确定,首先根据自重应力进行计算,其次在边坡模型的制作过程中,考虑到对砂土的击实,故在自重应力的基础上额外增加4 kPa的应力。

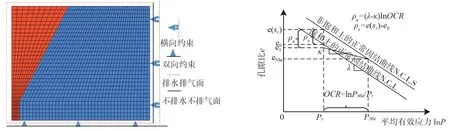
图2 数值计算模型及边界条件 图3 非饱和土及饱和土的e-lnp曲线Fig. 2 Numerical calculation model and boundary conditions Fig. 3 The e-lnp curve of unsaturated soil and saturated soil

表2 砂土物理特性表Table 2 Physical properties of sand

表3 砂土的材料参数表Table 3 Material parameters of sand

图4显示了A、B这2层土样土-水特征曲线的实验数据与计算曲线。从图中可知,计算曲线能较好地拟合实验数据。计算曲线是基于ZHANG等[18]提出的SWCC模型而得,计算所用的土-水特性曲线模型参数列于表4。在边坡模型进行摸拟降雨实验前,先测其4个工况A、B土层土样的初始负孔压值。因为边坡模型的尺寸较小,故可以将初始气压视为大气压力,其大小设定为0 kPa。为了方便计算,根据实验测得的初始负孔压值,将4个工况边坡的每层土整体都取为同一个负孔压值。并通过图4的土-水特征曲线,确定计算的初始饱和度,见表5。

表4 A、B层砂土的土-水特征曲线参数表Table 4 Parameters of the soil-water characteristic curves of the A、B layer sand

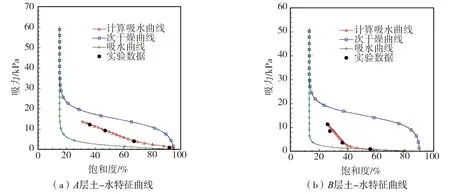
图4 A、B层土-水特征曲线Fig. 4 Soil-water characteristic curves of layer A、B

表5 计算初始负孔压值和初始饱和度Table 5 Calculation of initial negative pore pressure and initial saturation

一般而言,非饱和土的透水系数与其饱和度相关。文中基于MUALEM[20]所提的公式来确定A、B这2土层土样饱和度与透水系数的关系。从图5可知,A、B层土样的透水系数随着饱和度的增大而增大。

图5 饱和度与A、B土层透水系数的关系Fig. 5 Relationship between saturation and permeability coefficient of A、B soil layer

由于实验所用的砂土透气性较好,模型的尺寸不大以及模型的3个边界都为透气界面,因此在实验过程中产生的空气压力很小,可忽略不计。在此文中不再过多探究气压对于边坡雨水入渗破坏的影响。

2.2 数值计算结果与实验对比分析

4种工况实验和计算结果的对比见图6。在初始阶段,各点位的负孔隙水压都趋于平稳。随着降雨的持续进行,各点位的负孔隙水压依次在某段时间内快速上升。实验和计算曲线终止的时间点为边坡破坏时刻。从图6可知,4种工况的计算结果在总体上与实验数据吻合,可以较为准确地反映在不同降雨强度和坡角条件下,边坡各点位负孔隙水压随时间的变化过程以及预测边坡破坏的时间。但是,计算曲线最后达到稳定时的负孔隙水压值总是高于实验结果。其产生的原因是,计算所用的土体透水系数相对偏小,使得雨水在渗入土体时滞留增多。

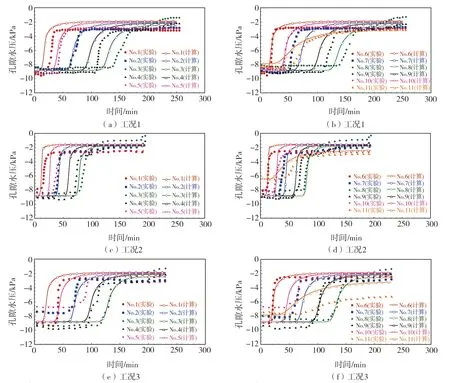
图6 负孔隙水压力的计算值与实验值的对比Fig. 6 Comparison of calculated and experimental values of negative pore water pressure

2.3 边坡水分迁移的计算结果分析

饱和度和吸力值具有一一对应的关系,饱和度越高,则吸力值越小,见图4。故可从吸力在各时间点的变化来反映边坡的水分迁移。图7为4种工况在50 min和坡体破坏时吸力的计算结果云图。雨水是从A层土体的顶部流入,并向下渗透。在初始阶段A层土体的透水系数高于B层,故在短时间内(50 min)B层只有少量的土体受到了渗透。边坡破坏时底部吸力值仍然大于上部,其原因在于边坡底面为排气排水面,水可从底面排出,边坡底面不会出现大量积水。

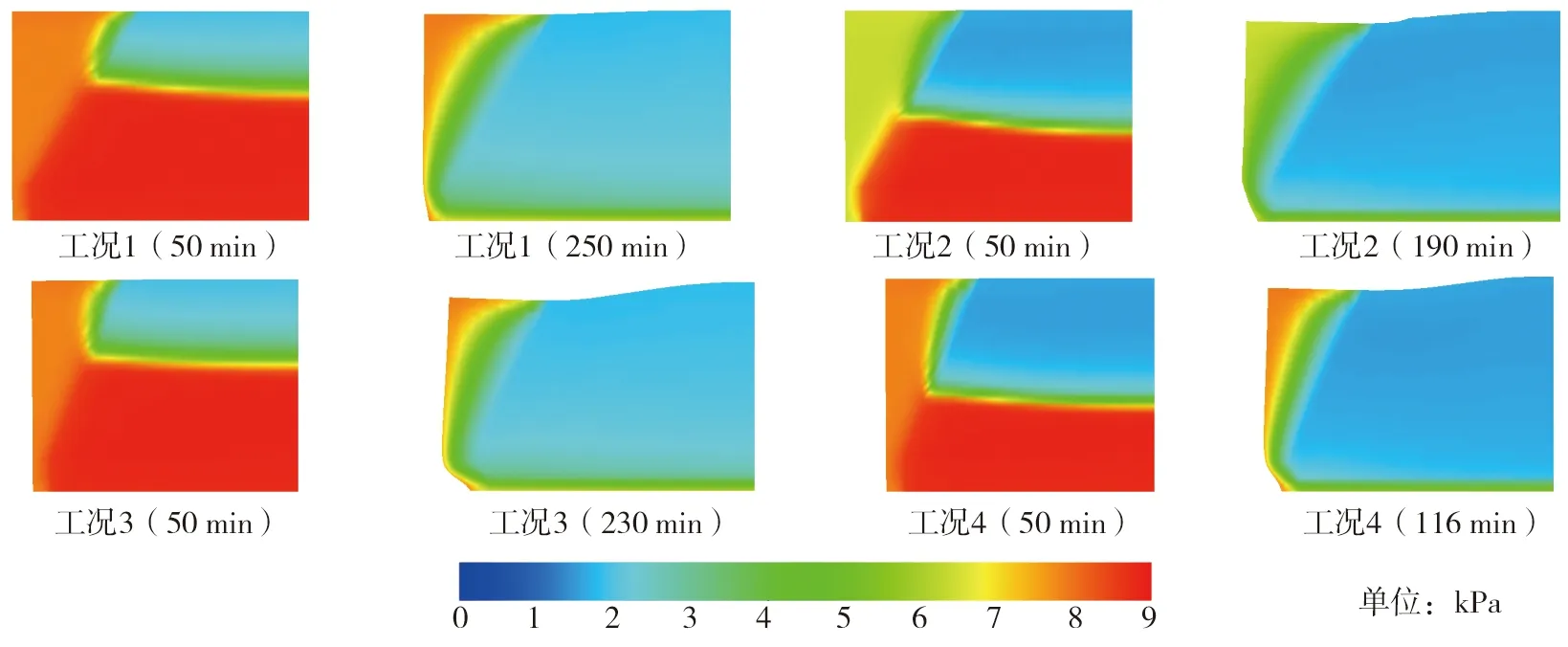
图7 各工况的吸力分布图Fig. 7 Suction distribution diagram of various working conditions

2.4 双层非饱和土边坡破坏机理分析

降雨入渗对于非饱和土边坡的影响主要在于:雨水渗入使得土体的重度增大,同时又使其基质吸力降低甚至丧失。在双重作用下,边坡发生失稳破坏。工况2的B层土的饱和度和其他几个工况不同,因此不将其作为对比实验进行分析。

2.4.1 边坡破坏时间的分析

实验和计算曲线终止的时间点为边坡破坏的时刻,见图6。3个工况破坏所需的时间从长到短依次为:工况1(250 min)、工况3(230 min)、工况4(116 min)。影响边坡破坏时间的因素主要有2点:1)从图1可知,模型1的坡角(59°)小于模型2(68.3°),从力学平衡分析,模型1边坡的稳定性高于模型2。2)从降雨条件分析,工况3的降雨强度(50 mm/h)小于工况4(100 mm/h),即相同的时间内,工况4的累计雨量大于工况3和工况1,从而加快边坡的失稳破坏。

2.4.2 边坡塑性破坏带形成过程的分析

图8为边坡破坏前后瞬时塑性剪切应变分布的计算结果。从3个工况的云图可知,在边坡遭受破坏以后,都有一条明显的塑性剪切带贯穿整个边坡。其所在的位置皆在两土层交界面偏向A层一侧。其原因是雨水渗入整个边坡后,由于两土层渗透性的差异,使得A层的渗透程度远高于B层,即A层的吸力小于B层(如图7所示),因此破坏带主要在A层形成。从3个工况边坡破坏前后的变化可知塑性破坏带的演化过程,即塑性破坏从左侧的坡趾附近开始,随着降雨的进行逐渐蔓延至坡顶,形成一条滑动破坏带,最终导致边坡发生渐进性倒坍滑动破坏。

图8 各工况边坡模型破坏前后的塑性剪切应变分布Fig. 8 Plastic shear strain distribution before and after failure of the slope model under various conditions

2.4.3 降雨强度对边坡破坏影响分析

图9为工况3和工况4边坡破坏后的位移矢量图。矢量的方向表示土体滑动方向。2个工况的左侧土体整体向下滑动。可从图9中很明显地发现滑动带的具体位置。工况4滑动的土体规模小于工况3。造成上述现象的原因是:从累计雨量来看,两者大致相同(工况3降雨强度50 mm/h,历时230 min;工况4降雨强度100 mm/h,历时116 min)。从图7可知,工况4中水从A层渗入B层的量相对较少,使得更多的水滞留在A层中,导致工况4的A层基质吸力小于工况3,此现象也可在图6中得到佐证。因此相比于工况3,其滑动带的位置会发生上移。

图9 破坏后的边坡模型位移矢量分布Fig. 9 Displacement vector distribution of the slope model after failure

2.4.4 塑性剪切带上单个单元的应力路径分析

图10给出了工况3模型中某2个单元的应力路径。图10(a)为选取单元的示意图,选取临界破坏面上C点和塑性带外一点D。图10(b)中横轴表示平均有效应力,纵轴表示广义剪切应力,随着时间的推移,将获得的C点和D点的平均有效应力和剪切应力大小在图10(b)中绘出。从图中可知,当雨水渗入土体中后,土体内部的孔压逐渐上升,土骨架的有效应力逐渐减小。2个单元的应力路径不断向横轴的负方向移动,与此同界破坏面上C点首先达到临界状态线,表明塑性破坏带内的单元已到达临界状态线,此时土体发生了破坏,当C点达到临界状态线时,D点还未达到临界状态线,表明塑性带外的单元没有达到临界破坏状态,并未产生明显滑动。

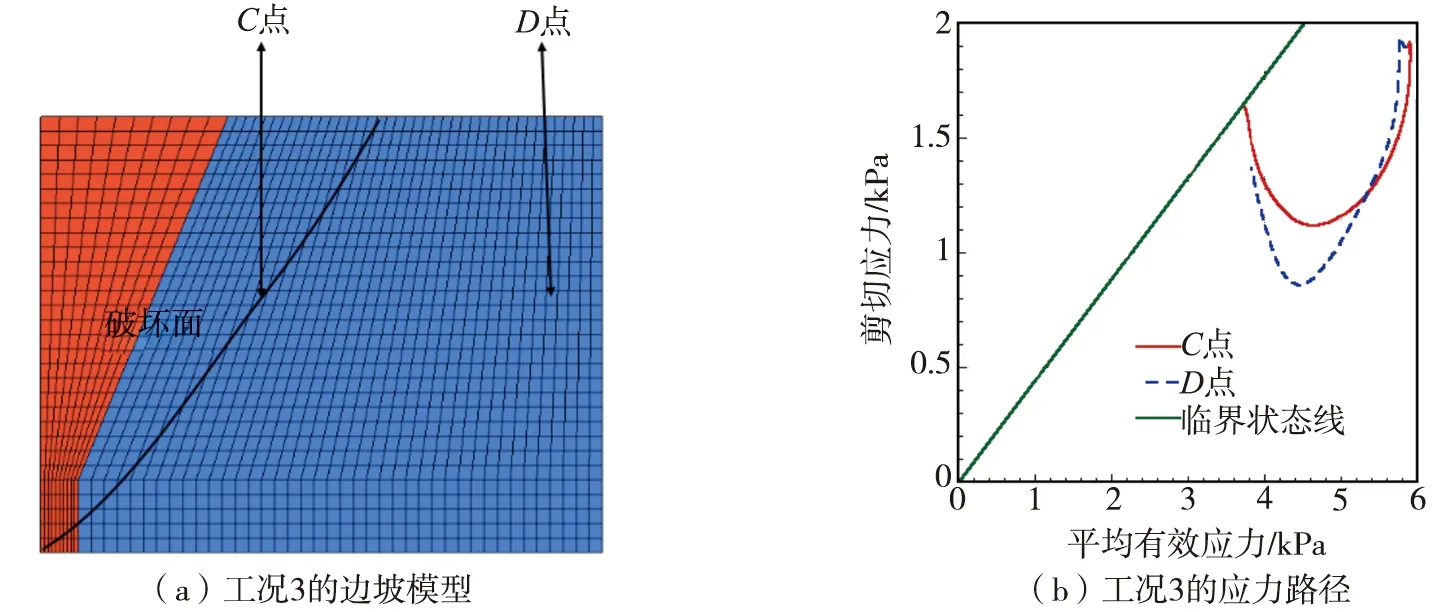
图10 塑性剪切带上的单元位置及其应力路径Fig. 10 Element position and stress path on plastic shear band

3 结论

为研究不同降雨强度和坡度的双层非饱和土边坡的破坏机制,文中基于ZHANG等[18]提出的以饱和度和Bishop有效应力为状态变量的非饱和土本构模型,将其导入土-水-气三相耦合的有限元程序中,并对KITAMURA等[19]的室内边坡降雨破坏模型实验进行数值模拟,得出了如下结论:

1)负孔隙水压的计算结果较为准确地拟合实验数据,表明文中所提的数值计算方法能在同一套参数下较好地模拟不同降雨强度和坡角的双层非饱和土边坡的破坏实验。 计算结果得到了边坡2个土层之间水分迁移的变化情况。开始阶段,水由A层顶部渗入,随后开始向A层土体的底部蔓延,水分由A层渗入B层较为缓慢。

2)降雨强度与坡角的不同会影响边坡发生破坏的时间。坡角越小或降雨强度越小,边坡越不易发生滑动破坏。计算结果揭示了非饱和土边坡塑性破坏带形成的过程。随着降雨的进行,边坡的塑性破坏首先在左侧的坡趾附近形成,然后逐渐延伸至坡顶,形成一条贯穿整个边坡的塑性剪切带,最后边坡左侧的土体整体沿着滑动带下滑。此外,还可得到降雨强度对边坡滑动规模大小的影响,即在总降雨量大致相同时,低强度长历时的降雨使边坡滑动的土体体积更大。相比于双层坡体,单层边坡在A、B层交界面两侧的吸力变化相对平稳。将B层置换成A层砂土后,整个坡体的抗渗能力有了明显的提升。

由于文中选取试验为小尺寸的室内实验,模型的三边皆为透气透水边界,且试验所用的砂土透气性较好。因此没有探究气压对于坡体破坏的影响。若采用大尺寸的边坡模型或者试验土样的透气系数较小时,可能将产生较大的气压,今后,将会在这些方向上进行探究。