发射药冲击破碎对埋头弹装药燃烧和内弹道性能影响的数值模拟

熊佳敏,陆 欣

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

引 言

火药多为黏塑性材料,具有低温冷脆性能。当火药药粒在炮膛内受到挤压冲击碰撞时,产生的膛内压力发生异常,超过药粒自身承受力时,火药就会变形甚至产生裂痕发生破碎。大量发射药药粒骤然发生破碎且破碎程度较为严重时,会引发火药燃面的急增,药粒燃气生成速率随之猛增,膛压飙升,特别在弹丸起始运动阶段。这就是“挤压-破碎-增燃-升压”共识的理论形成[1-2]。大量研究表明,在发射过程中若火药药粒出现严重破碎,易形成恶劣的膛内力学环境,并出现膛炸等发射安全性事故或火药粉末性破碎转化成爆轰[3-5]。

现阶段学者采用多种方法探究药粒破碎对火炮发射安全性的影响。陈言坤等[6]采用燃气生成速率比表征火药破碎程度,并采用密闭爆发器测定撞击后的破碎发射药压力曲线,获取破碎程度量化值验证此定量方法是合理可行的;王燕等[7]阐述了形状大小不一破碎发射装药在气固两相流过程中的等效形状函数与等效形状特征量的确定方法,为火药破碎状况提供一种新的计算方式;杨超[8]结合火药颗粒破碎实验结果分析火药颗粒受撞击后的应力应变特性,证明火药颗粒在超过屈服速度撞击下的破碎必然性,引入燃面变化并设定不同的破碎条件探索颗粒破碎对弹道参量的影响。

作为一种特殊装药结构的新型弹药,埋头弹弹丸放置在药室定向筒内部,采用二次点火及程序燃烧原理[9-10]。唐群英等[11]在模拟弹丸膛内运动过程中,利用改进的非支配排序遗传算法优化相对装药量及装填密度,结果显示弹道效率保持不变的情况下埋头弹炮口速度有所提高;陈玉璐等[12]基于埋头弹点传火特性建立零维内弹道模型,应用一维身管传热模型数值分析了单发和连发射击时的管壁传热规律。

当火药颗粒不能适应埋头弹特定的点火条件、装药结构条件等引发的膛内力学环境,导致点火异常,不能按照程序着火燃烧,使得在点燃前火药发生严重破碎的概率大大增加,极大地影响到埋头弹发射过程。本研究根据火药冲击破碎变化机理进行理论分析,结合火药破碎结构形状对燃面产生的影响,挖掘火药燃面与形状的深度联系,为展现火药床的运动、挤压与破碎,建立考虑火药破碎的一维两相流理论模型,分析发射过程中的物理量分布,预测发射药粒在点传火过程中的受力、破碎、燃烧以及膛压异常变化等内弹道性能,以期为研究发射装药的发射安全性提供新的手段。

1 火药冲击破碎机理

1.1 破碎度

为了定量描述含能颗粒床的破碎程度,翁春生等[13]提出破碎度的概念。将火药颗粒破碎后的总燃烧面积与标准未破碎火药总燃烧面积之比定义为破碎度,即:

(1)

式中:Sbr、Sst为火药破碎后总燃面与标准未破碎火药总燃面;m为火药破碎程度等级数;ηi为每个等级中火药质量的百分比;M0与Mi分别为单颗火药颗粒的质量和该等级中火药碎粒的质量;S0与Si分别为单颗火药颗粒的燃面和该等级中火药碎粒的燃面。

在火炮两相流模型中颗粒间挤压应力是造成火药冲击碰撞破碎的关键因素。本研究采用Kuo等[20]通过实验得到的颗粒间应力公式:

(2)

(3)

(4)

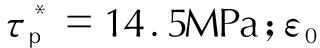
上式适用于从火药颗粒填满空隙、火药床弹性变形以及破碎的全过程。

通过其高低炮压撞击破碎实验分析数据结果发现,在某一温度下破碎度与最大挤压应力成线性关系:

(5)

式中:τ1、τ3、Br1与Br2为火药药粒冲击破碎实验测得数据。即当某一瞬间获取到挤压应力时,便能根据该公式预测这一时刻的火药颗粒的破碎度,得到药粒燃烧表面增大比例。本研究采用文献[13]实验所得数据,即τ1=9.9MPa,τ2=15.8MPa,Br1=1.71,Br2=2.67。

1.2 理想化破碎

忽略颗粒形状差异性,假设火药颗粒力学性能等条件相同,火药药粒遭到冲击破碎时产生形变发生理想化破碎,即需要满足以下条件:(1)根据质量守恒关系总质量、总体积不发生改变,火药破碎前后只发生形状变化;(2)根据火药燃烧规律,火药燃烧一段时间后的形状相似于原来形状,颗粒采用几何燃烧定律,火药破碎前后依然保持平行层燃烧。

理想化破碎模拟如图1所示。由图1可知,一颗单孔管粒状火药理想化破碎成n颗碎粒。平行层燃烧原则显示一个火药颗粒着火一段时间后,均在其表面燃烧相同的厚度,形状由图1(a)变为图1(b)。此时模拟碰撞冲击,火药横向破碎,均等份分裂成n颗大小一致,长度仅为原来的n分之一的颗粒,图1(b)破碎为图1(c)。

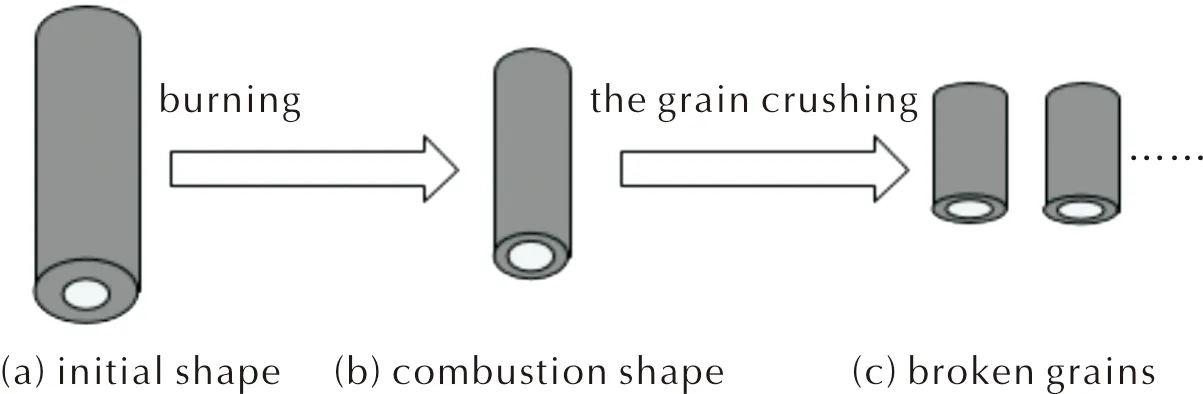
图1 理想化破碎模拟图Fig.1 Idealized fracture simulation diagram

模拟破碎完成,可直观观测到单个颗粒破碎前后总燃面面积。药粒形状变化如下:

(6)

单孔管粒状在此过程中燃面变化为:

(7)

式中:n为火药破碎碎粒颗数;Z为火药已燃相对厚度;e为火药颗粒在这一段时间燃烧的厚度;e1为初始火药粒起始厚度的一半;未燃烧时发生破碎时Z0=0;d与D为管粒状火药内径与外径,d0+4e1=D0;c为破碎后火药长度的一半;Sin为破碎后增加的燃面面积。

在得知预测下的破碎度时可获取到n碎粒颗数:

(8)

图1(c)中的碎粒相当于类似形状的火药燃烧e厚度得来。将火药颗粒破碎后的燃烧规律等同于此类似火药,根据推导计算可知火药破碎后的模拟火药的尺寸参数:

(9)

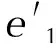
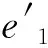
由于管状药粒形状参数μ为0,可忽略。基于形状特征量基础公式模拟火药的形状参数为:

(10)

1.3 实际破碎的修正

由于实际状况下药粒破碎有可能出现缺角、表面弯曲等细微差别,不一定完全符合上述理想化规律进行破碎。故为减少偏差且简便计算,直接将形状特征量参数各自乘以修正系数ηχ、ηλ以表征实际火药不规则破碎模型中的特征值参量,即:

(11)

可通过管粒状火药粒挤压破碎实验获取实际火药破碎表燃面Sid,与理想化破碎火药的表燃面S′比较获得,即:

(12)

管粒状相对燃烧面积为σ=1+2λZ,ξ也为:

(13)

因此,可得:

(14)

结合固相药粒全部燃烧成气相燃气时,火药颗粒消失,即火药相对厚度为1,药粒相对燃烧质量为1,即:

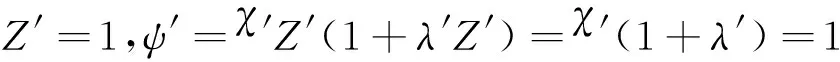
(15)

即ηλ与ηχ也需满足下式:

(16)

即可在确定ηλ与β′时获取ηχ。

综上所诉,根据实际火药破碎状况修正形状参数公式:

(17)

将修正后的火药形状参数参与到一维数值仿真模拟中,能较为准确地表现出点火异常时火药药粒实际破碎的膛内状况。

2 埋头弹两相流模型

埋头弹独特的装药结构及其二次点火程序燃烧机制在体现优越性的同时,也形成了膛内更为复杂的两相流动过程。装药结构图如图2所示。

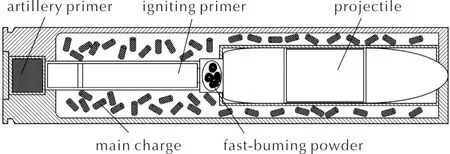
图2 埋头弹装药结构图Fig.2 The charge structure drawing of CTA

由图2可知,埋头弹区别于其他常规弹药在于弹丸置于身管膛线起始部前方定向筒内,主装药装载在弹丸周围,并将少量速燃药放置于弹丸底端。埋头弹有序燃烧下,底火射流击发后率先点燃速燃药颗粒,带动自身及周围主装药在弹底小范围剧烈运动。弹丸尾部达到启动压力后,先行在定向筒自由滑动并缓慢向炮口运动。因此在主装药点燃前,弹丸具有一定的速度从而减少了火药与弹丸的相对速度,减轻了火药药粒在弹底的撞击,缓解了火药颗粒在弹底的挤压冲击过程。与此同时,底火射流点燃主装药床,当弹丸推入膛线时全面着火燃烧,大量高温高压燃气释放,推动药粒从膛底向弹底运动并堆积挤压,部分主装药碎粒和燃气随之流入身管,形成了疏密不均的火药分布,最终弹丸冲出炮口完成发射过程。

若埋头弹未按照正常的点火程序点燃底火、速燃药及主装药,会产生点火异常现象,如埋头弹发射前期出现传火管泄漏或者导向管异常破裂问题,高温点传火气体提前进入主装药粒区域,主装药先行着火,其释放的高压燃气增多,增大气固运动速度,靠近弹底的药粒拥有更大的碰撞速度。上述破坏了原有点火程序的异常现象都将导致火药遭到强烈的挤压冲击而破碎,其火药燃面增大。火药颗粒的状态显著地影响到后续埋头弹膛内气固变化和两相流动。针对埋头弹特殊内弹道过程的特点,简化物理模型,在发射主装药燃烧全部结束之前,考虑火药破碎带来的膛内气固两相间相互作用及运动变化,建立考虑药粒破碎的埋头弹一维两相流内弹道数值模型并模拟仿真。

2.1 控制方程组

根据埋头弹药的结构特点以及点火方式,埋头弹火炮内弹道膛内气固两相流的守恒方程[16-17]如下:

气相连续方程:

(18)

固相连续方程:

(19)

气相动量方程:

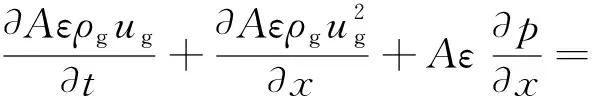
(20)

固相动量方程:

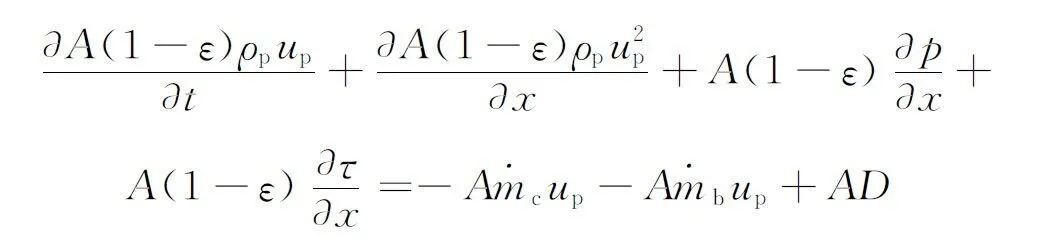
(21)

气相能量方程:

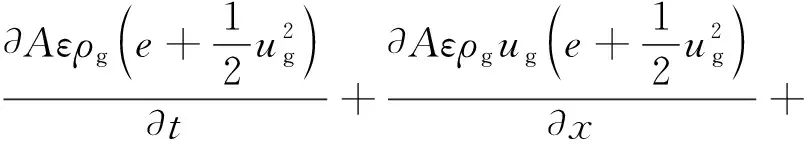
(22)

2.2 辅助方程

部分相关辅助方程公式显示如下,其他详见文献[18]。

发射主装药形状函数为:

(23)

(24)

式中:ψc为主装药相对已燃质量;Zc为主装药已燃相对厚度;σc为主装药相对燃烧表面;Sc为一颗主装药未燃烧部分燃面积;S1c为一颗主装药初燃面。

火药总燃面及燃气质量公式为:

(25)

(26)

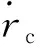
2.3 边界条件与初始条件

(1)弹底边界。由于弹丸在身管向前运动,弹底边界为运动边界。在弹底运动控制体上根据边界的守恒推导所需物理量,还应满足弹丸运动方程:

(27)

式中:pd为膛内弹底压力;f为弹丸横截面遭受的阻力;mq为弹丸质量;v为弹丸速度。

(2)膛底边界。将膛底看成静止固定壁面,采用反射法将边界点内化获取弹底物理量。

(3)初始条件。埋头弹射击过程开始时的膛内状态作为初始条件,其中,气相与固相速度为0,温度为常温,压力为大气压。

3 预测结果及其比较

采用Mac Cormack差分格式和CFL稳定条件编程计算得到各埋头弹一维两相流各物理参量,分析预测火药破碎前后的炮膛力学环境,包括火药破碎状况、药粒间挤压应力、膛压与气相速度等随时间随空间的膛内变化规律以及压力波动情况,为解决埋头弹发射安全性问题提供了基础依据。

3.1 挤压应力与破碎度

颗粒间挤压应力是导致火药破碎的一个重要因素。不同时刻挤压应力分布曲线如图3所示。由图3(a)可明显观察到,在点传火阶段由于受到火炮内壁的限制,在弹底和膛底出现火药床的压缩,火药颗粒间产生挤压应力并向内部扩散,弹底及靠近弹底处挤压比膛底严重许多。此外,速燃药在靠近弹底位置燃烧,使得周围膛内环境压力、温度达到主装药的着火条件,引起主装药颗粒燃烧,堆积的主装药颗粒减少,膛内空间变得稀疏,火药颗粒遭受的火药颗粒与火药燃气、火药颗粒与火药颗粒、火药颗粒与炮膛内壁的相互冲击减少,即在速燃药位置挤压应力有显著的凹陷。与普通弹药相比,速燃药的一次点火缓和了颗粒间的撞击,减缓了弹底挤压应力的增大,这也进一步反映出特有的速燃药装药结构也是埋头弹发射装药发射安全性的关键。

图3 火药未破碎与模拟破碎不同时刻挤压应力分布曲线Fig.3 Crushing stress curves of non-fragmentation and simulated fragmentation at different instants of time

埋头弹点火异常情况下,在某些位置点处在强烈的挤压应力的作用下火药颗粒发生仿真模拟破碎。比较破碎前后的τ变化,由图3(b)可以发现,模拟破碎后τ在x=0.12～0.18m之间有着显著的增大,τmax从24.7MPa增大到35.1MPa,颗粒间挤压应力作用持续时间也明显增长。这表明火药颗粒的变形破碎会使得火药在发射过程中受到更强烈的冲击,达到更大的挤压应力,进而使得更多颗粒产生破碎且碎粒颗数增多,如此恶性循环,进一步证明如果火药颗粒发生大量破碎,将产生严重后果。

不同位置挤压应力随时间的变化曲线如图4所示。由图4可知,变化曲线在发射阶段存在两处鼓包:第一处鼓包为点火传火初期,第二处鼓包为弹丸挤进阶段的射击初期,此时挤压应力在药室各处急速增加。在火药颗粒未破碎时弹底处增加较多,受速燃药燃烧的影响,主装药在速燃药及膛底之间最易发生破碎,使得在t=6.5～8.0ms时挤压应力在x=0.17m处飙升最多。8.0ms后由于主装药全体着火燃烧且弹丸运动后弹道空间变大,火药颗粒更加稀疏,挤压应力减小直至没有。在某一瞬间某一位置的挤压应力飙升,易引发不稳定状态导致膛炸事故的产生,尤其对于力学性能不佳的火药,可通过改善埋头弹挤进条件降低挤压应力增大引发的风险。

仿真火药破碎时不同时刻的破碎度分布曲线如图5所示。

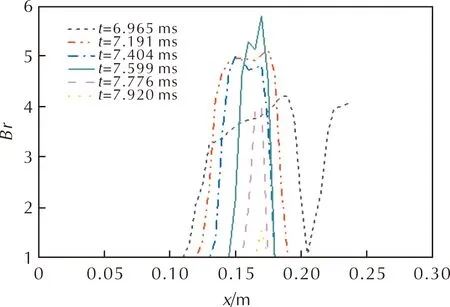
图5 火药模拟破碎时不同时刻的破碎度分布曲线Fig.5 Distribution curves of fracture degree of simulated fragmentation at different times

由图5可知,颗粒间应力越大,药粒破碎越严重。根据τ与Br的线性公式,Br与τ趋势相似,在挤压应力未达到临界应力时,火药颗粒可能一些变形但不足以破碎,破碎度依旧维持在1,对射击过程不产生影响。挤压应力达到临界应力后,随着挤压应力的增大,破碎度也随之增大,即火药燃面增加,模拟火药药粒的破碎状况越发严重,对膛内气固两相间的作用及运动变化影响愈大。破碎主要集中在x=0.12～0.18m处,Br比例最大,达到5.8。

通过分析挤压应力与破碎度的模拟计算结果,发现可从两种途径减缓颗粒间的冲击破碎:首先在装药方面,埋头弹火炮需采用动态力学性能较好的火药,减少变形,扩大其破碎临界应力,降低发射主装药颗粒的冷脆性,减少低温下的破碎,使x=0.12～0.18m处的破碎度集中降低;其次在装药结构方面,应设计合理的传火管及导向管的长度与强度,使得射流能有序稳定点燃速燃药及主装药确保实现点传火及程序燃烧有序进行,也能承受较大冲击,避免出现提前破裂状况,降低颗粒与弹丸的撞击可能性。

3.2 压力分布与压力波

随着膛内火焰的传播,因火药颗粒逐渐被点燃颗粒间挤压应力消失,燃气压力升高。不同时刻膛压分布曲线如图6所示。由图6(a)可知,火药未破碎时膛压曲线更加平滑。假设埋头弹异常点火后添加火药破碎模型,碎粒会导致燃面增加,燃气生成速率加快。当弹后空间的扩展程度跟不上燃气产生程度时,会导致破碎位置的压力异常激增,压力随着时间进而向整个药室及身管传递拓展,各位置膛压都有一定程度的增加,当压力变化超出炮膛机械强度时,易引发灾难性事故。图6(b)中曲线也清晰展现出在火炮局部膛压出现异常波动,证明异常压力在火药冲击破碎现象下极易出现。

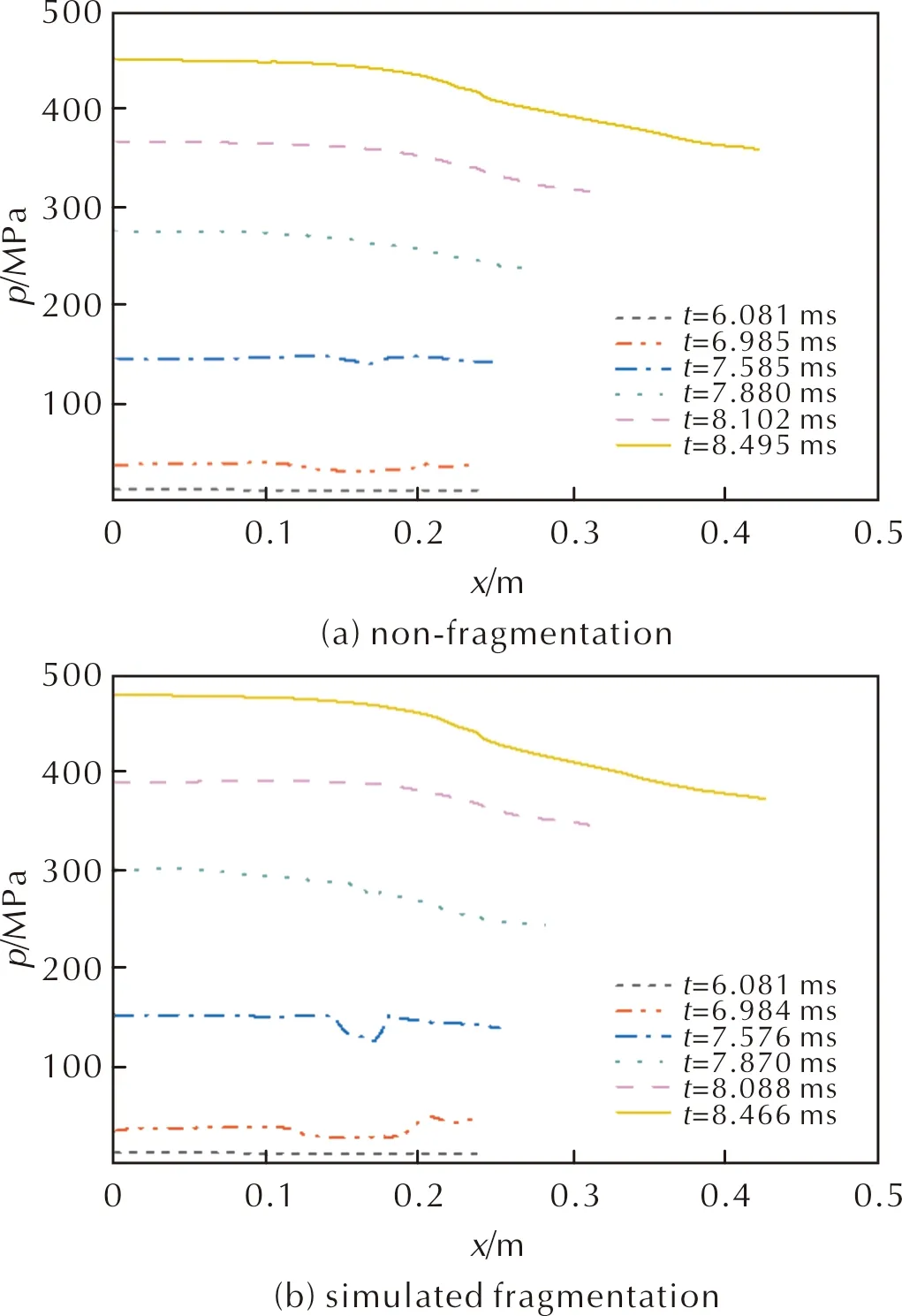
图6 火药未破碎与模拟破碎不同时刻膛压分布曲线Fig.6 Pressure curves inside the chamber of non-fragmentation and simulated fragmentation at different instants of time

膛底压力和弹底压力随时间的变化曲线如图7所示。

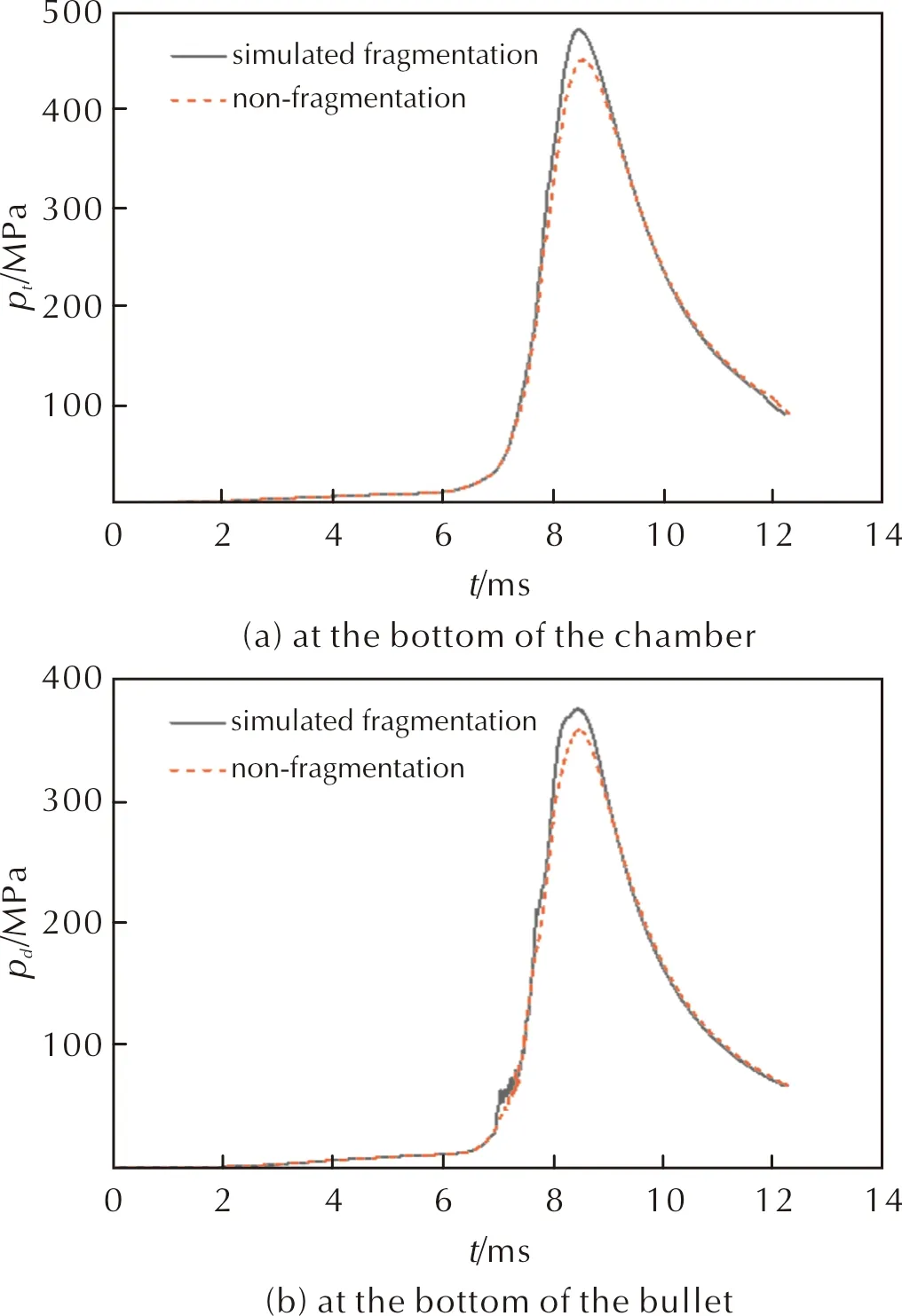
图7 膛底压力和弹底压力随时间的变化曲线Fig.7 Pressure curves with time at the bottom of the chamber and at the bottom of the bullet

由图7可知,火炮开始发射时,底火射流导致膛底主装火药先开始燃烧,膛内放出高温高压燃气,此时的膛底压力高于弹底压力,火药颗粒推动向弹底运动,在弹底位置产生冲击挤压现象,严重时产生破碎。紧接着当弹底压力反高于膛底压力时,造成足够大的反向压力梯度,颗粒会发生反射效应产生向膛底运动的速度,因此颗粒在弹底及膛底如此往复运动。合理匹配埋头弹点传火条件,可减少弹丸挤进阶段以及运动初期存在着的药粒破碎使压力骤然增长的可能性。火药模拟破碎的最大膛底压力为481.5MPa,最大弹底压力为375.3MPa,如表1所示,是未破碎的1.069倍及1.047倍,数值结果揭示了火药破碎增压现象。压力波变化曲线如图8所示。

图8 火药未破碎与模拟破碎压力波曲线Fig.8 Pressure wave curves of non-fragmentation and simulated fragmentation

由图8可知,压力波曲线可定义为膛底压力与坡膛处压力之差随时间的变化曲线,可用来表示膛内压力过程的波动性。-Δpmax是指压力波曲线上最大负峰值,可表征膛内压力波的强度。由表1可知,药粒未破碎的曲线-Δpmax为-2.6MPa,而参与破碎为-11.0MPa,且+Δpmax为22.6MPa,破碎为33.8MPa,表明火药颗粒破碎加剧了埋头弹内弹道流场的波动性,是造成大振幅压力波的一个重要原因。此外,压力波在6.5～8.8ms发生较大振幅的上下起伏,火药模拟破碎后起伏更加剧烈,说明若在此时间内火药发生意外破碎,产生反常危险压力波的可能性大幅增加。

3.3 弹丸速度与气相速度分布

弹丸速度随时间和行程的变化曲线如图9所示。

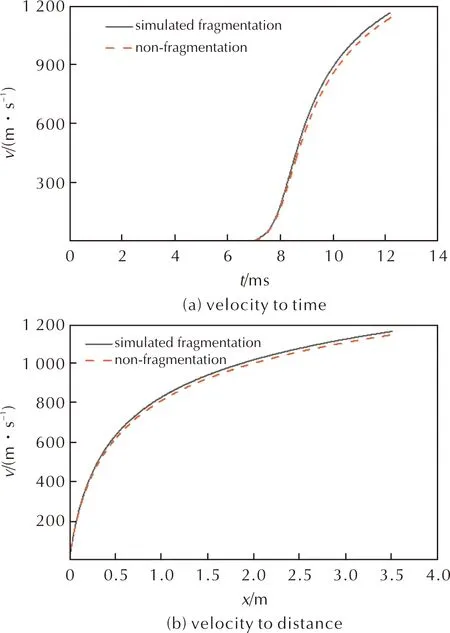
图9 弹丸速度随时间和行程的变化曲线Fig.9 Curves of the projectile velocity with time and distance

由图9可知,火药未破碎的炮口初速v0为1146m/s,模拟破碎增至1163m/s,证明火药颗粒的破碎会导致炮口初速的增加。弹丸速度在相同的时间点都有一定程度的增加,且随着时间和行程的增长斜率更大,这是因为火药破碎增大其颗粒燃烧表面,从而加剧其燃烧效应。火药固相颗粒与其燃烧释放的高压燃气在膛内的运动是十分复杂多变的。不同时刻气相速度分布曲线如图10所示。

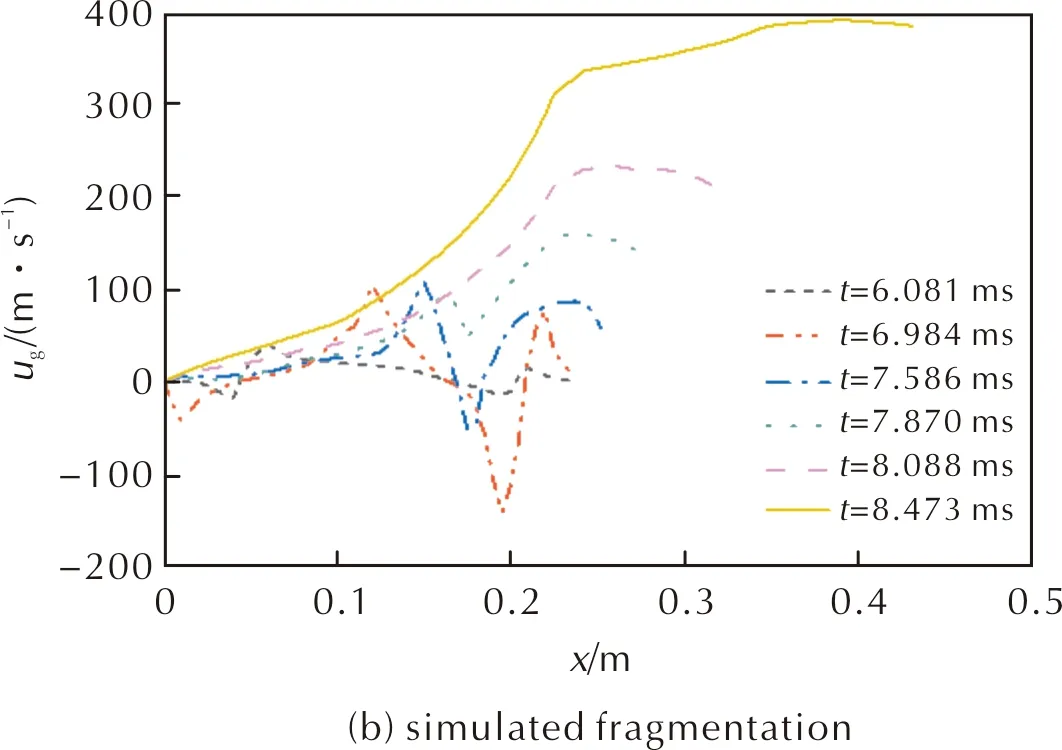
图10 火药未破碎与模拟破碎不同时刻气相速度分布曲线Fig.10 Distribution curves of the gas phase velocity at different time of non-fragmentation and simulated fragmentation

在弹丸未运动及挤进阶段,对比图10未破碎与破碎状态,颗粒破碎时每一时刻气体在膛内达到的最大负流动速度和最大正流动速度都更大,鼓包程度加大,反映出在埋头弹内弹道循环过程中火药药粒破碎引发的燃气的大量生成会影响到膛内的气体流动状态。药粒破碎时更多燃气的冲击碰撞以及更大压力的驱使挤压使得火药颗粒药床内弹道运动更多变,气体流动更加波动及剧烈。

4 结 论

(1)点火异常下的火药破碎使得颗粒间的冲击作用加强,挤压应力在破碎位置迅猛增加,最大挤压应力也从25.7MPa增至35.1MPa。同时破碎度燃面比例跟随挤压应力变化增大到5.8。证明埋头弹装药设计中需要合理的装药和点火程序,大力改善埋头弹点传火过程出现火药破碎的情况,避免产生过强的颗粒间挤压应力。

(2)波动异常的膛压揭示了火药破碎使得在药床内部会形成局部异常压力。膛底压力升至481.5MPa,弹底压力升至375.3MPa,是未破碎的1.069倍及1.047倍,显著升高的数值表明了火药破碎增压机制。增大的振幅及强烈起伏的压力波阐明了药粒破碎加强了两相流流场的波动性。这对研究埋头弹火炮异常压力机理及压力波的抑制提供有益的理论指导。

(3)药粒破碎后炮口初速v0增加到1163m/s,以及气相速度鼓包程度的加大,反映了火药药粒的破碎使得埋头弹内弹道循环内气固两相火药颗粒运动及气相流动更复杂多变,膛内相互作用更为剧烈。因此研究药粒破碎对射击过程的影响对埋头弹火炮有着重要意义。