氮/氧杂环含能材料晶体密度的预测研究

吕志涛,刘玉存,聂江稳,贾康辉,李 强

(1.中北大学 环境与安全工程学院,山西 太原 030051;2.山西兴新安全生产技术服务有限公司,山西 太原 030024)

引 言

含能材料是武器系统实现推进、毁伤的化学能源,对其研究包括分子、晶体、配方和应用等方面,其中含能分子的设计和合成是含能材料研究和发展的基础。为了适应现代武器高安全、高可靠和高效毁伤的发展要求,钝感及高能量密度成为含能材料追求的主要目标。氮、氧杂环含能材料由于具有高正生成焓,密度大,燃烧产物多为无毒气体等优点[1],是设计和合成钝感高能含能材料理想的结构单元,其中杂环结构单元包括吡唑、咪唑、三唑、四唑、呋咱、吡啶、三嗪、四嗪环等,通过引入取代基如:硝基、氨基、硝酸酯基、硝胺基、叠氮基、肼基等含能基团,另有偶氮基等连接单元,可以构建出大量含能材料分子。如果盲目合成这类含能材料再进行筛选则非常困难,预先进行能量特性预测再进行目标化合物合成可大大减小合成工作量。

密度是含能材料重要的能量特性参数,与其他参数如爆速、爆压等有密切关系。因此,建立精准的密度预测模型对含能分子进行预测筛选,可以剔除性能不佳的含能材料的研制工作,避免不必要的人力、时间和资金的浪费。目前,含能材料密度的理论预测方法主要有等电子密度法、分子表面静电势法、基团加和法、定量构效关系法等[2]。每种方法各有优势与局限性,运用时需综合考虑各方面因素。

最早提出预测密度的方法是基团加和法[3],将原子和官能团的体积相加得到分子摩尔体积。此法简单但是无法区分组成相同而分子构型、构象不同对密度的影响。等电子密度面法是利用量子化学方法计算出0.001a.u.等电子密度面包围的体积作为分子体积,进而由摩尔质量与分子体积的比值求出晶体密度。邱玲、肖鹤鸣等[4]采用此法,比较了45种硝铵类化合物在不同基组下的密度。Rice等[5]研究了180个中性分子和38个高氮分子,均方根误差在4%以内。然而在某些情况下误差较大,可能是没有考虑分子间相互作用。故Politzer等[6]将分子表面静电势引入,对等电子密度法进行校正,误差有显著的改进。Rice等[7]运用Politzer[6]提出的修正方法,用之前研究的化合物验证得出该校正方法提高了预测精度。因此分子表面静电势法在分子设计与性能预测方面得到了广泛的应用。

最初构建结构与性能定量关系的计算方法是以多元线性原理为基础[8]。冯雪艳[9]运用多元线性回归对36种多硝基芳香族化合物,以官能团个数为自变量,对密度进行预测;来蔚鹏[10]选取最弱键长、旋转键、氢键供体、中点势、分子总能量等描述符对30种芳香系单质炸药利用多元线性回归建立密度预测模型;Narges Zohari等[11]将唑类含能材料的元素组成、化合物不饱和度、硝基亚胺基以及一些结构性参数的贡献值建立了一种新的回归模型。此方法原理较简单,但需分析所选取的自变量与因变量的线性相关性,且各自变量间不存在极强的多重共线性等适用条件。近年来,机器学习逐渐被用来预测含能材料的性质,它可以对已有数据特征进行提取和建模,预测未知含能材料分子的性能。其中,神经网络算法因其自身的特点和优越性,应用愈发广泛,可以用作分类、聚类、预测等。而BP神经网络,是一种按误差逆向传播算法训练的多层前馈网络,结构简单,是目前应用最广泛的神经网络模型之一,可用于函数拟合、预测等方面。于国强等[12-16]运用神经网络分别建立了撞击感度、炸药临界直径、热感度、生成焓、密度、爆速的预测模型。上述文献研究,模型都达到了一定的预测精度,但是样本数量较少,适用范围有一定的局限性。因此,针对数据集小,一种特殊的机器学习——深度学习,越来越受到重视。陈杰[17]从剑桥晶体结构数据库中筛选出2000条只含有硝基的化合物数据,分别基于随机森林和图神经网络建立了含能材料密度预测模型;陈超等[18]基于空间矩阵特征化的方法建立了精确的机器学习模型,降低了预测的平均绝对误差;Alex等[19]采用分子三维电子结构为描述符,基于卷积神经网络得到含能材料包括晶体密度的8种主要性质的预测模型;Phan Nguyen等[20]将高能化合物化学结构转化为RDKit二维分子描述符作为输入,以信息传递神经网络模型预测密度。这些深度学习算法都获得了较高的预测精度,但是需要大量的数据集,经过特征编码以及矩阵运算,对专业知识及硬件要求非常高。

氮、氧杂环含能材料作为合成高能量密度材料的一种选择,有必要对这类含能材料建立较为精准的密度预测模型,为新型杂环含能化合物的筛选提供理论依据。鉴于已合成的氮、氧杂环含能材料的数量有限,且结构参数和性能参数的匮乏,不适合选用深度学习算法,因此本研究采用与文献[6-7]相同的泛函以及M06-2X泛函,在原有参数下添加其他合适的结构参数,分别采用多元线性回归(MLR)和BP神经网络建立密度预测模型,以比较不同泛函对密度预测精度的影响,并与文献[6-7]方法进行比较,得到一种分子结构与密度的关联模型,提高预测的准确度和可靠性,为新一代高性能含能分子设计提供理论指导。

1 实 验

1.1 样本数据计算与收集

本研究杂环含能材料样本数据通过查询《含能材料及相关物手册》《火炸药手册》《四唑类富氮化合物研究》等书籍及与含能材料相关的期刊文献,收集到杂环含能材料共112种,其中包括10种吡唑类、6种咪唑类、18种三唑类、24种四唑类、29种呋咱类、9种三嗪类、8种四嗪类和8种吡啶类,并从手册和CCDC数据库中查询各物质标准状态下稳定晶型的密度实验值,将其记录并保存。

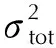
1.2 研究方法

计算和查询到的共10种结构参数在建立模型时需进行变量的筛选来确定引入模型的变量。有的参数可能对密度的影响不是很大,而且各参数之间不完全相互独立,可能有互相作用的关系。因此,这里利用逐步回归方法筛选并剔除引起多重共线性的变量。基本思想是将变量逐个引入模型,并对引入的变量进行F检验,对已经选入的变量进行t检验,当原来引入的变量由于后面变量的引入变得不再显著时,则将其删除。如此反复,直到既没有显著的变量被选入,也没有不显著的变量被剔除为止。这样建立的回归模型预测效果会更好。同时尝试用筛选出的参数建立BP神经网络模型。为了验证模型的可靠性,采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方误差(MSE)、均方根误差(RMSE)、相关系数(R)、决定系数(R2)评价。其中,平均绝对误差、平均绝对百分比误差、均方误差和均方根误差可以从整体上评价模型预测的误差大小,数值越小说明模型预测的精度越高。相关系数和决定系数越接近于1,表明所建立的模型效果越好。

2 结果与讨论

2.1 多元线性回归模型的建立

多元线性回归模型考虑的是多个因素对同一个因素的影响,即多个自变量与因变量的关系,可表示为:

yi=b0+b1xi1+b2xi2+…+bpxip

(1)

式中:yi为预测值,x1、x2……xp为p个自变量,b0为常数项,b1、b2……bp为回归系数,采用矩阵形式求出每个回归系数。

为了验证所建立的模型有良好的外部预测能力,将112个样本数据集随机分为训练集92个,用于建立模型。剩余20个化合物作为测试集,验证该模型的预测能力。首先选用B3PW91/6-31G(d,p)下计算所得参数,采用SPSS软件进行多元逐步回归,结果见表1。

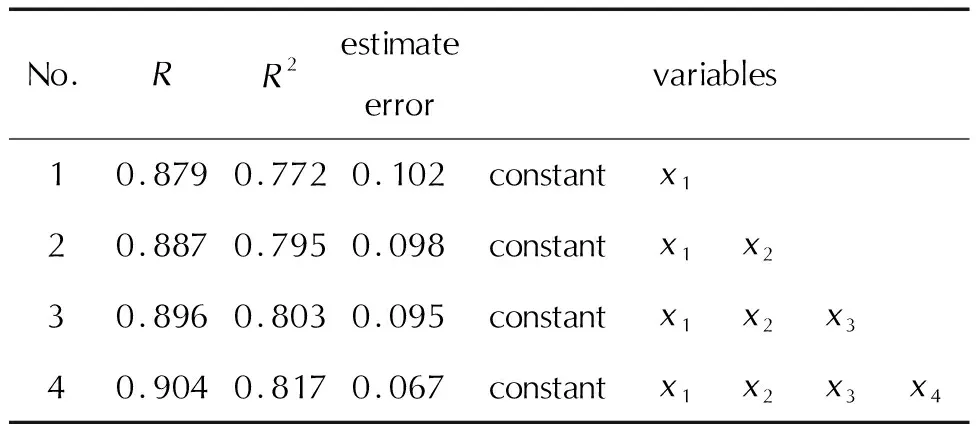
表1 多元逐步回归结果Table 1 Results of multiple stepwise regression

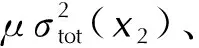
表2 模型系数Table 2 Parameters for models

分别将训练集与测试集中的化合物各参数代入上述模型,计算得到的预测值与实测值作对比,结果见图1和图2。由图1可知,3种计算理论水平下,数据较集中的分布在对角线附近两侧,说明该模型有一定的预测能力。由图2可知,随着预测值的变化,残差均在一定的水平带状范围内波动,说明模型效果较好,由于少数误差较大的点使得带状区域较宽,预测精度不是很高。经比较,在B3PW91泛函下计算所得参数建立的MLR模型对于训练集和测试集的平均绝对误差、平均绝对百分比误差、均方误差均低于B3LYP泛函和M06-2X泛函计算结果,而相关系数和决定系数高于B3LYP泛函和M06-2X泛函。M06-2X泛函计算结果稍好于B3LYP泛函,具体各评价指标见表3。但是从整体分析得出,3种理论水平下建立的MLR预测模型精度都不高,预测结果不是很好,由此考虑采用其他方法建立模型。因BP神经网络能学习和存储大量的输入与输出之间的映射关系,无需事前提供描述这种映射关系的数学方程[13]。因此,尝试采用相同的训练集和测试集,建立BP神经网络模型预测杂环含能材料的晶体密度。

图1 MLR模型预测值与实测值比较Fig.1 Comparison of predicted value obtained by MLR model and experimental value

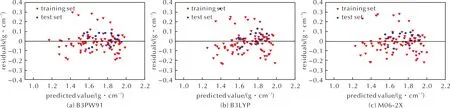
图2 MLR模型预测值与残差的关系Fig.2 The relationship between predicted value obtained by MLR model and residual

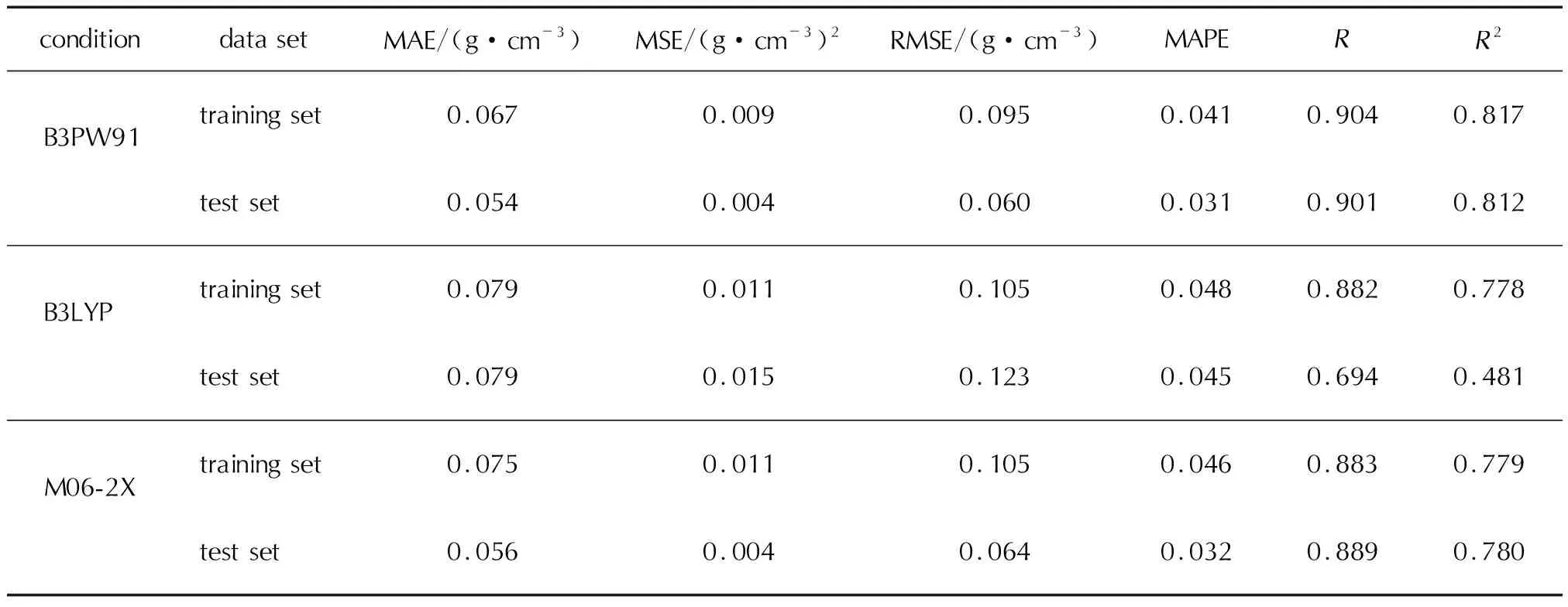
表3 MLR预测模型的评价指标Table 3 Evaluation metrics for MLR model

2.2 BP神经网络模型的建立

由BP神经网络模型的拓扑结构可知,BP神经网络的构建需确定输入层、隐含层和输出层。由逐步回归方法筛选出的参数可知,有4个输入参数和1个输出参数,但隐含层数和节点数是不确定的。为了提高网络训练精度,一般采取增加节点数和隐含层数的方法。但是在网络结构实现上,增加节点数要比增加隐含层数简单,因此选择单隐含层。而隐含层节点数的确定,目前在理论上还没有作出明确的规定。一般根据经验公式,在一定范围内,采用尝试法,通过对不同节点数进行训练对比,选取最合适的网络[25]。

BP神经网络不同的传递函数、训练函数会影响网络预测结果。具体参数设定为:学习速率0.01,训练次数1000次,训练目标最小误差0.0001。在MATLAB中编写程序完成算法过程。分别在不同的传递函数、训练函数和隐含层节点个数下进行训练,经过多次训练得到测试集预测的精度最好时的网络结构为4-7-1。

BP神经网络模型的预测值与实测值比较结果如图3和图4所示;BP预测模型的评价指标见表4。由图3和图4可以看出,对于训练集和测试集,数据整体上较为紧密地分布在对角线附近,残差点也分布在较窄的带状区域内,且B3PW91泛函计算结果优于B3LYP泛函和M06-2X泛函,B3LYP泛函和M06-2X泛函计算结果相差不大。同时由表4可知,和多元回归模型比较,平均绝对误差、平均绝对百分比误差、均方误差均有所降低,而相关系数、决定系数均有所提高,说明BP神经网络模型较多元回归模型的预测效果好,预测精度高。

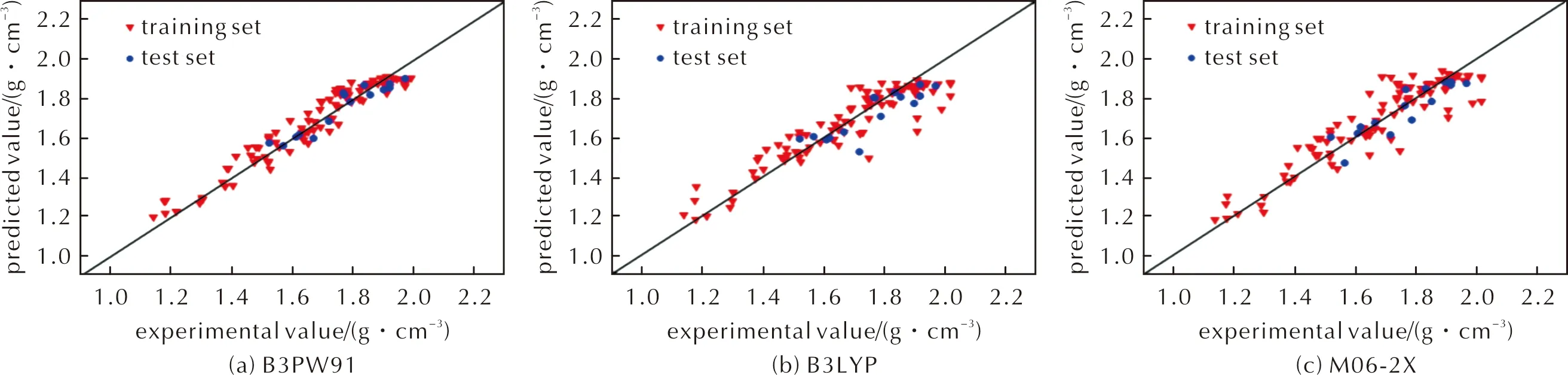
图3 BP模型预测值与实测值比较Fig.3 Comparison of predicted value obtained by BP model and experimental value

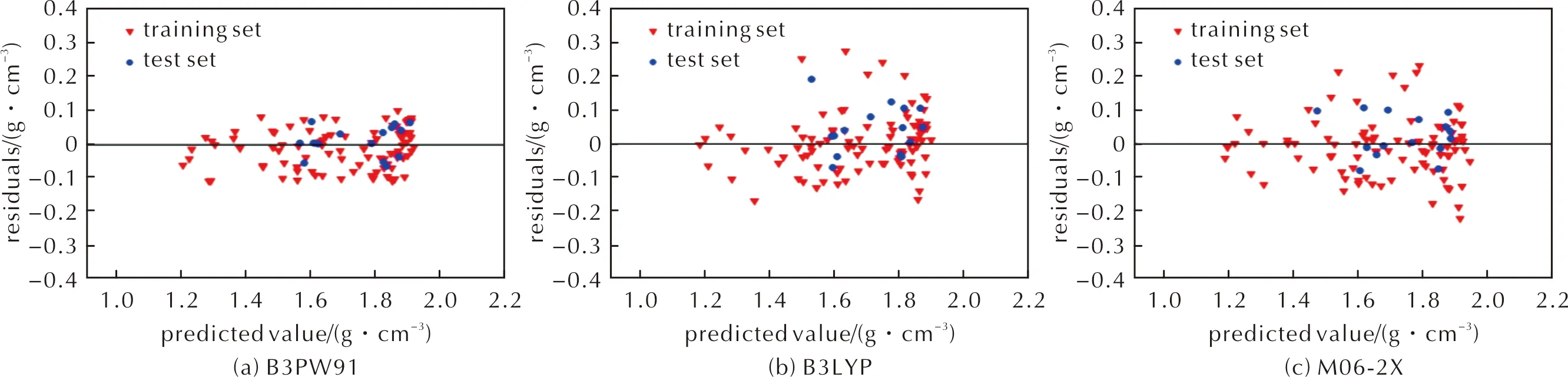
图4 BP模型预测值与残差的关系Fig.4 The relationship between predicted value obtained by BP model and residual

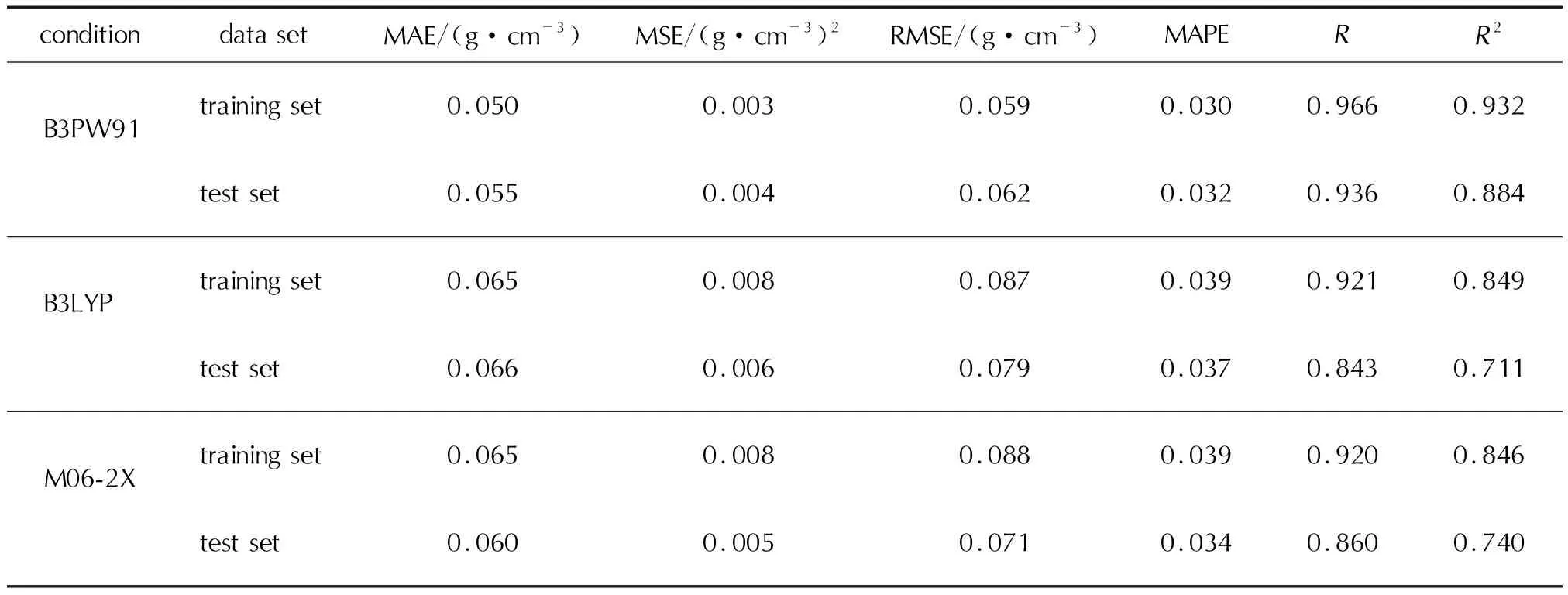
表4 BP预测模型的评价指标Table 4 Evaluation metrics for BP model

2.3 预测模型评估与比较

为了评估模型的可靠性和稳定性,除了应用测试集对模型进行验证外,同时采用留出法将样本数据进行多次建模后取平均值作为评估结果,并与Politzer等[6]和Rice等[7]提出的预测公式进行比较,相关评价指标见表5。

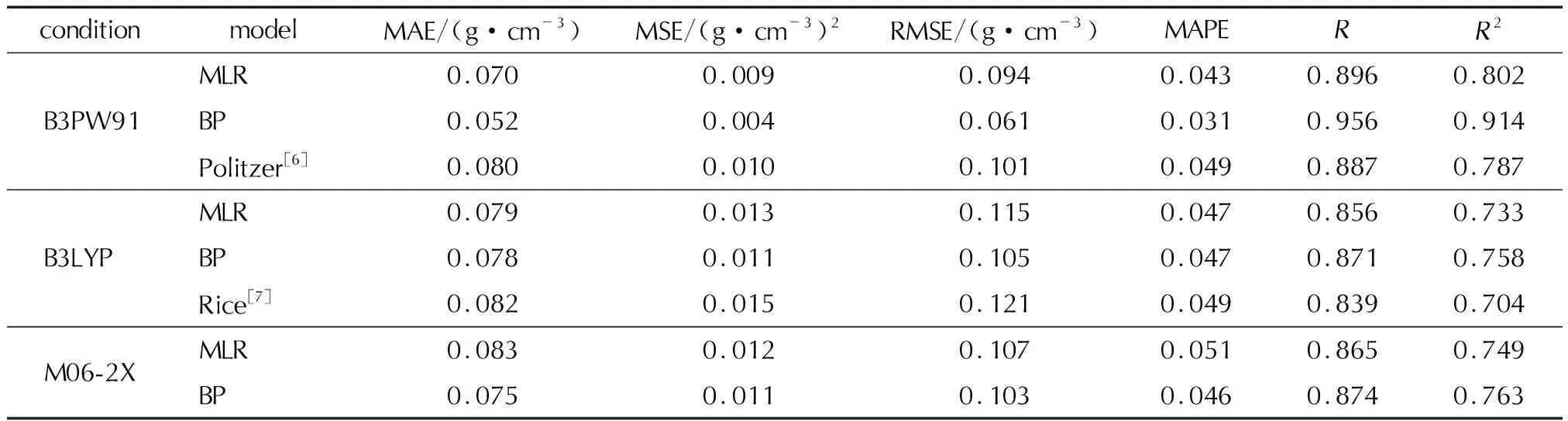
表5 所建模型与现有模型的比较Table 5 Comparison of the established models and the existing models

由表5评估结果可知,3种泛函下计算所得参数建立的模型,B3PW91泛函结果优于其他两种。在B3LYP/6-31G(d,p)水平下,平均绝对误差、均方误差、平均绝对百分比误差,MLR模型预测结果较Rice等[7]的计算结果分别降低了0.003g/cm3、0.002(g/cm3)2、0.002,而BP神经网络预测模型分别降低了0.004g/cm3、0.004(g/cm3)2、0.002,结果较好于MLR预测结果。同样,在B3PW91/6-31G(d,p)水平下,MLR模型预测结果较Politzer等[6]的计算结果分别降低了0.01g/cm3、0.001(g/cm3)2、0.006,而BP神经网络预测模型分别降低了0.028g/cm3、0.006(g/cm3)2、0.018,结果仍然优于MLR预测结果。总体可看出,对于氮/氧杂环含能化合物在原有分子静电势法的基础上添加了氢键供体数和氢键受体数两个参数后,预测精度提高,且在B3PW91/6-31G(d,p)水平下,BP神经网络建立的密度预测模型精度最高,但是没有达到最理想的效果,可能与量子化学计算方法所得参数的精度及样本数量有关。BP神经网络由于具有较强的映射能力,能够通过学习自动提取输入、输出数据间的“合理规则”,通过反向传播不断调整网络的权值和阈值,使网络的误差平方和最小,得到比多元回归模型较好的预测结果。

3 结 论

(1)运用量子化学计算方法,分别选择B3LYP泛函、B3PW91泛函和M06-2X泛函,在6-31G(d,p)基组水平下对112种氮、氧杂环含能材料的分子结构进行优化,分析其振动频率后得到最稳定分子结构,检索出7类量化结构参数,并从PubChem数据库查询到3类结构参数,为建立模型统一了结构参数的来源。

(2)通过逐步多元回归方法筛选出对密度影响较大的参数并分别建立回归模型和BP神经网络模型,结果表明,在3种泛函计算水平下,均为BP神经网络模型的预测误差较小、精度较高。

(3)添加氢键供体数和氢键受体数两个参数后,与已有模型比较,MLR和BP神经网络模型的预测精度均有所提高,且在B3PW91/6-31G(d,p)水平下,BP神经网络模型的预测精度最高。