针对UNGM模型的特性分析与滤波算法设计研究
卢山, 张世源
(1.上海航天控制技术研究所, 上海 201109; 2.上海市空间智能控制技术重点实验室, 上海 201109)
随着航天器在深空探测、国防、导航通讯等多个领域发挥着越来越重要的作用,人们对航天器导航、制导与控制精度的要求也越来越高。准确的状态估计是航天器实现轨道、姿态自主控制、执行深空探测、在轨服务等空间任务的前提[1]。随着任务需求的变化,航天器的运动学、动力学模型越来越复杂,在轨运行环境不确定性因素越来越多,许多研究机构和学者改进和提出了各类非线性滤波算法[2-3]以获得更高的状态估计精度。
单变量非平稳增长模型(univariate nonstationary growth model,UNGM)是用于验证非线性滤波算法的基准模型,在滤波器设计与评估类文献中被广泛使用[4-10]。该模型的状态方程具有很强的非线性,而且在观测yk是关于状态xk的偶函数时其状态的后验概率密度呈双峰特性[11],即状态量在2个不同区间内取值的可能性接近,这大大增加了对状态量进行准确估计的难度。基于以上原因,UNGM的状态估计是一个复杂的非线性递推贝叶斯滤波问题,对于滤波器性能的要求非常高[12]。但是自文献[13]首次将该模型应用于验证非线性滤波器性能以来,鲜有文献针对该模型的性质进行分析研究。由于该模型特性较为复杂,使得一些研究,如文献[14-16]对该模型的使用存在不恰当之处。无迹卡尔曼滤波器(unscented Kalman filter,UKF)[17]是一种经典的非线性滤波器,经常在滤波器设计类文献中被用作对比仿真试验的基准滤波器。由于UKF属于Sigma点卡尔曼滤波器,即采用确定性采样的方式获取采样点,其采样点的数量以及分布范围均受限。当待估计状态量的后验概率密度呈双峰特性时,UKF所使用的采样策略无法同时获得状态量在2个概率密度峰值区间的统计信息,会使得UKF估计结果失准。基于上述原因,UKF在对UNGM进行估计时,会出现模态估计错误、状态方差发散等问题,同时会影响其作为对比仿真试验中的基准滤波器时,对滤波器性能进行评估的合理性。
粒子滤波(particle filtering,PF)[18]基于Bayes原理的序贯Monte-Carlo模拟方法,采样点数目与分布范围不受限制,能够对后验概率密度呈双峰分布的状态量进行估计。在PF中引入重采样以解决权值退化问题的滤波器称为自举粒子滤波器(bootstrap particle filtering,BPF)[5],是一种简单易行的粒子滤波器。但BPF仍存在计算量过大、模型针对性不强等问题,不是一种高效的滤波方法。
状态后验概率密度呈双峰特性的系统模型在工程应用领域也广泛存在:Duffing振子在谐和与随机噪声联合作用下的系统响应[19];油田产量和可采储量的二重二参数Weibull混合分布预测模型[20];毛细管-环电极配置的高压静电雾化系统下水静电雾化雾滴粒径的分布[21]等的状态量均具有显著的双峰概率密度分布规律。对UNGM模型的特性进行分析,设计一种能够有效应对UNGM的滤波器对于工程应用领域具有一定的借鉴意义。
1 UNGM特性分析
UNGM的离散化状态空间方程表示为
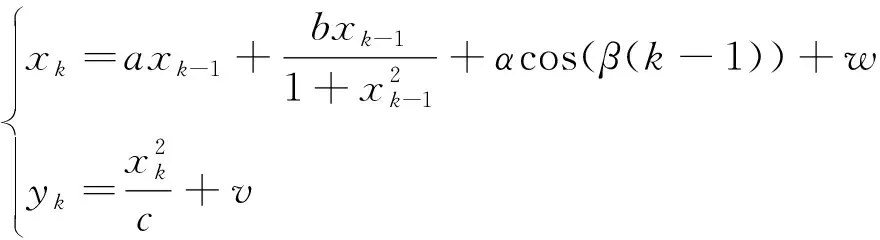
(1)
式中:a∈(0,1),b,c,α,β为模型系数,a与α对模型特性影响较大,可以根据研究所需的模型特性进行调整;w,v为过程噪声和观测噪声。
将状态方程中含状态变量项定义为
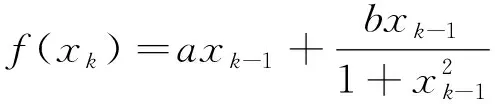
(2)
令a=0.5,b=25,c=20,α=0。假设状态初值x0服从均值为0的正态分布。UNGM的状态方程曲线及状态量在无噪声影响下的递推过程如图1所示。

图1 UNGM状态方程曲线
由图可知,当x0取值为一数值较小的正数时,由于f(x)在原点附近快速增长的特性,状态量会在下一时刻递推至一较大正数x1,并在后续时刻逼近状态方程函数y=f(x)与直线y=x在第一象限的交点(7,7)。易知该交点为状态量的一个平衡点,即处于该点的状态量受扰动偏离该交点后,均有返回该点的趋势。因此在系统噪声的作用下,状态量的值将围绕平衡点上下波动。
当x0取值为负时,递推过程与上述分析相同,此时的平衡点为状态方程函数y=f(x)与直线y=x在第三象限的交点。在不考虑余弦项与系统噪声时,状态方程为奇函数,故两平衡点关于原点对称。由于状态初值服从均值为零的正态分布,故x0取值为正数、负数的概率各占0.5,后续时刻的状态量将也以相等的概率围绕第一、第三象限的平衡点上下波动,这即是UNGM中状态量概率密度分布呈双峰特性的原因。
令a分别取值为0.5与0.9,其余参数不变。从均值为0,方差为1的高斯分布中取10 000个样本点作为状态量在k=0时刻的初始分布,将这些点代入到UNGM状态方程迭代5次,得到状态量在k=5时刻的概率密度分布如图2所示。
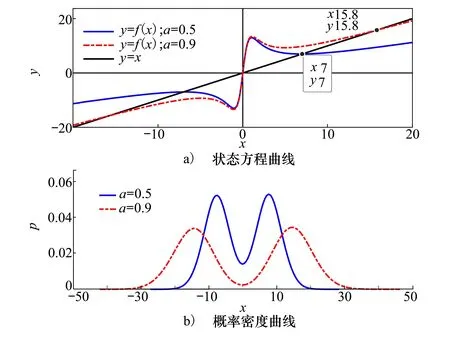
图2 参数a对函数特性的影响
由状态方程曲线可知,参数a对UNGM模型特性的影响主要在于状态方程函数y=f(x)与直线y=x交点的位置,即状态平衡点的大小。a取值越大,状态平衡点距离y轴越远。由概率密度曲线可知,状态量在k=5时刻的概率密度分布呈明显的双峰特性。分布峰值关于x=0对称,且a取值越大,峰值间距越大。
在a=0.5时,令β=1.2,α=8,其余条件不变。进行6次迭代,即令cos(1.2(k-1))近似变化一个周期,绘制k=1至k=6之间每一时刻的状态方程与概率密度曲线,如图3所示。
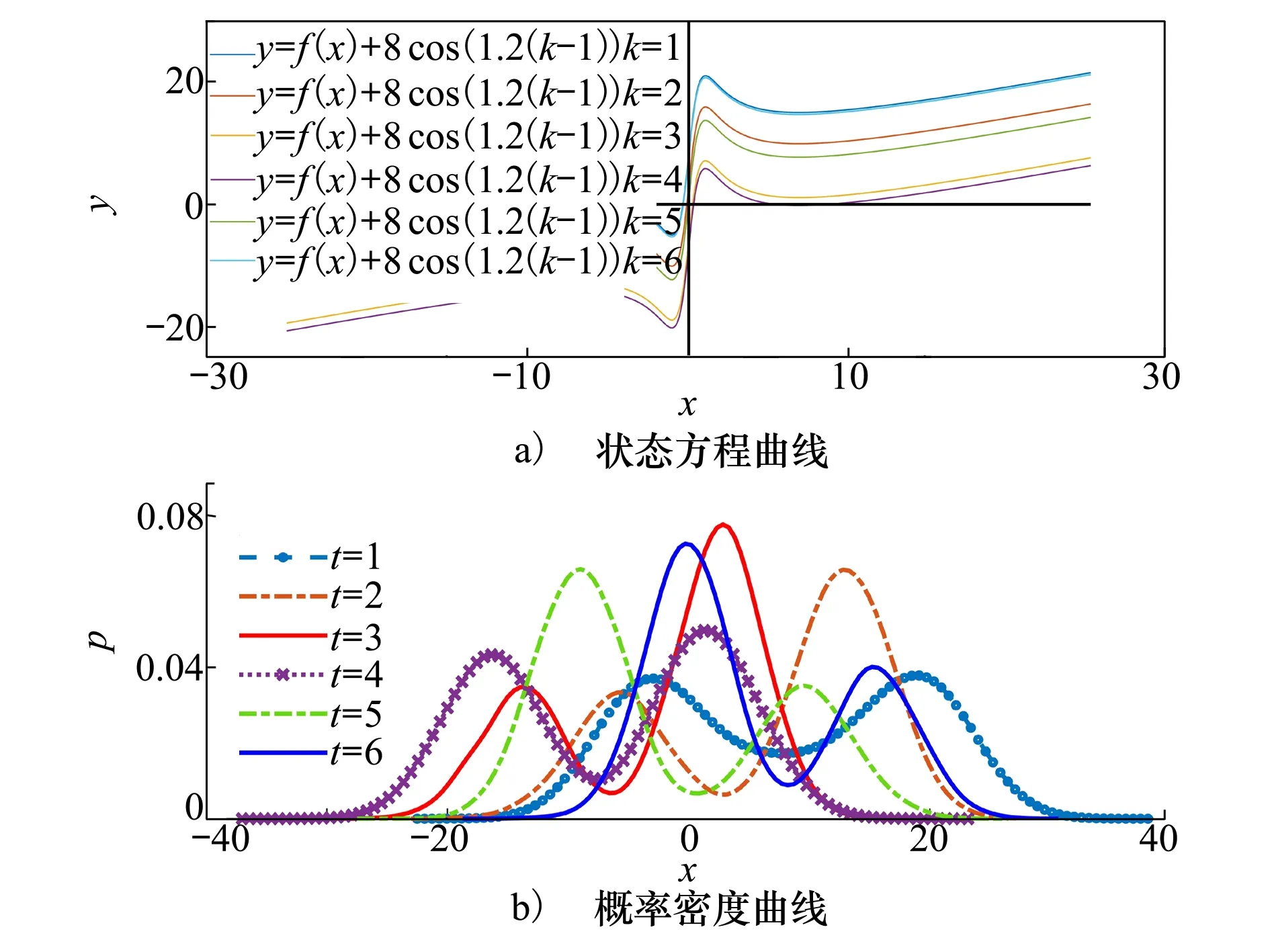
图3 参数α对函数特性的影响
如图3a)所示,αcos(β(k-1))的存在相当于在每一时刻的状态方程中引入一大小不同的常数,使得状态方程曲线沿y轴在[α,-α]的范围内上下移动,平衡点也随之上下平移,不再关于原点对称。由于平衡点不断发生变化,状态概率密度的峰值也不再关于x=0对称,同样在一定范围内呈类似周期性的变化。该变化范围的闭区间边界为αcos(β(k-1))=±α时,状态方程函数y=f(x)与直线y=x交点的x轴坐标值。
2 UKF失准问题分析及UNGM的常见使用误区
2.1 模态判断错误
模态判断错误这一失准问题的具体表现为:状态估计误差发散,状态估计方差收敛,状态估计值与状态真实值近似关于x=0对称。
模态判断错误发生的情况共有2种。第一种是由UKF的状态初值设置不当引起,文献[14]由于忽略了此类失准情况,造成对比仿真结论不合理;第二种是由过程噪声小概率发生的大幅跳变引起,文献[15]由于忽略了此类失准情况,造成对比仿真结论不严谨。


真实状态在系统随机噪声的作用下,可能由初始状态x0=0跳变至正值或负值,并稳定在UNGM位于第一或第三象限的平衡点附近。由于UKF无法对初始随机跳变的正负进行判断,故滤波器中的一步预测值xk|k-1与状态真实值xtrue可能正负异号,稳定于不同象限的平衡点。

图4 模态判断错误情况下的UKF估计情况
文献[14]认为这种情况是由UKF估计误差过大造成,进而得出UKF对非线性系统滤波性能不佳的结论。但该结论是不恰当的。由上述分析可知,UKF的模态判断错误是存在随机性的,并非在每一次仿真中都会发生。当UKF的模态判断正确时,仍能对UNGM进行较准确估计,具体表现如图5所示。
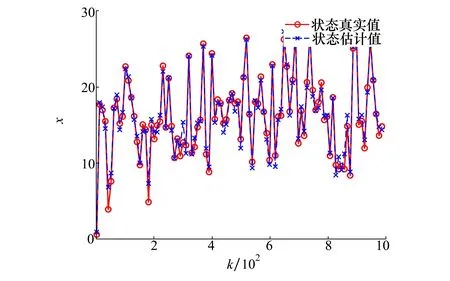
图5 模态判断正确情况下的UKF估计情况

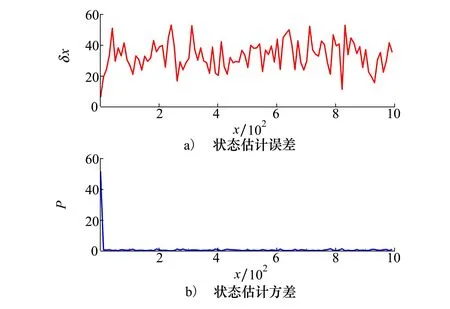
图6 模态判断错误情况下的状态估计误差与方差
第二种模态判断错误情况,如图7所示。虽然过程噪声w~N(0,10)的均值为0,但仍会有小概率出现幅值较大的情况。通常情况下,状态量会在过程噪声的影响下在某一平衡点附近波动。当滤波时间足够长,状态量便可能受到某一刻较大幅值的过程噪声值影响,正负号发生跳变,并迅速稳定至另一平衡点。本文将这种情况称为状态量的“模态跳变”。同样受量测方程为偶函数的影响,UKF无法识别这种模态跳变,发生模态判断错误。

图7 UKF模态判断错误
由UNGM特性分析可知,a的值越小,状态平衡点距离y轴越近,平衡点的值越小。这表示着w使状态量发生符号跳变所需的值越小,状态量在平衡点之间发生跳变的可能性越大,模态跳变越频繁。
文献[15]对状态量进行了100个时刻的滤波估计后,在估计误差收敛的情况下判定滤波器估计性能良好。这样的结论仍是不够严谨的,原因在于时间样本过少,未能包含上述状态量小概率发生模态跳变时模态判断错误的情况。
2.2 状态估计方差发散
状态估计方差发散的表现为:状态估计方差大幅震荡,在模态判断正确的情况下状态估计误差仍不能收敛,滤波器失效。此类情况由UKF的Sigma点分布不合理引起,文献[6,16]均由于忽略了此类失准情况,造成对比仿真结论不严谨。
按文献[6,16]进行参数设置,令a=0.5,α=8,β=1.2,其余条件不变。在这种情况下UKF的状态估计误差与状态估计方差曲线如图8所示。
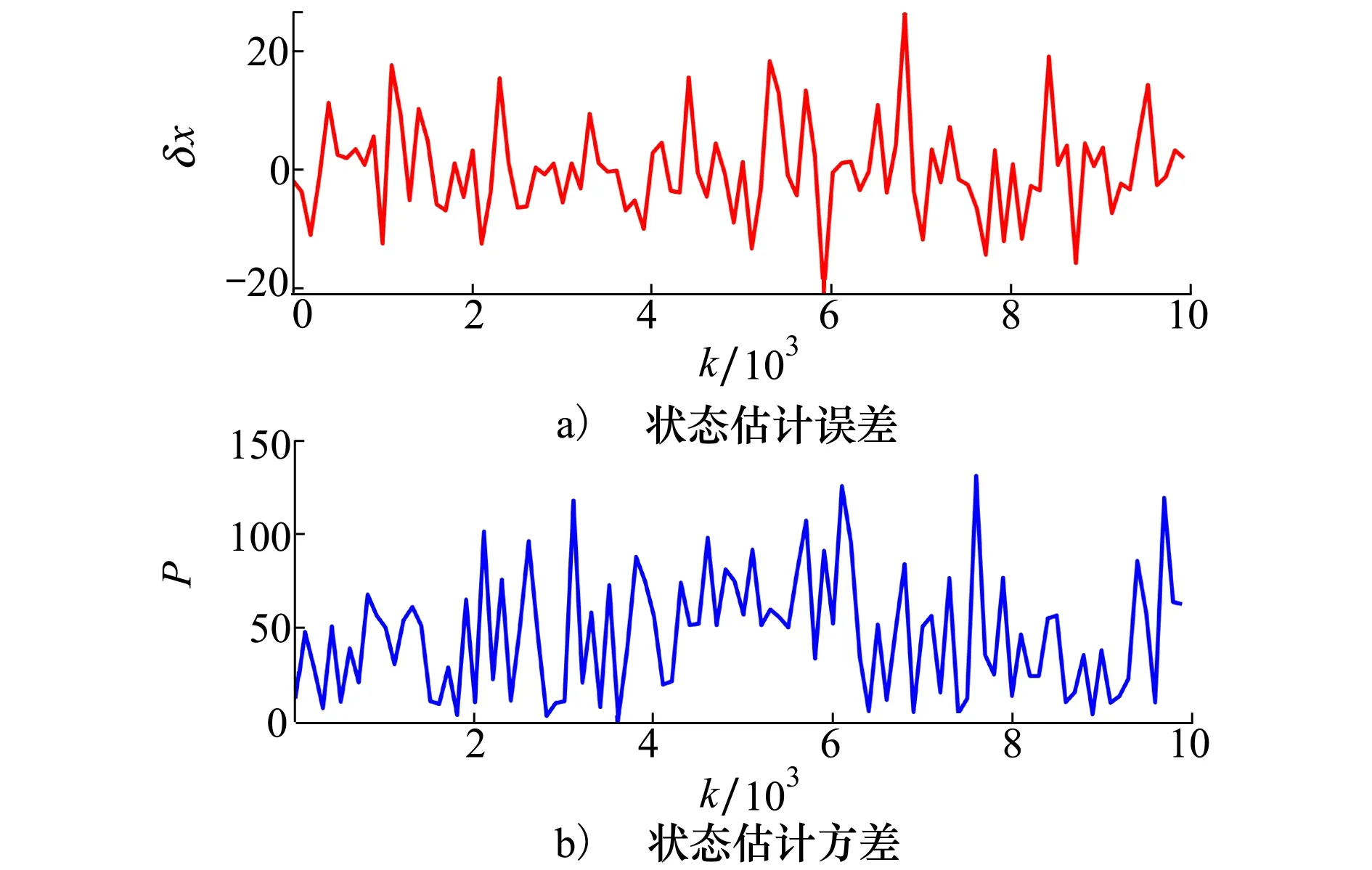
图8 状态估计方差发散情况
由图可知,在该条件下UKF状态估计误差发散,估计方差也未能收敛,滤波器处于失效状态。发生这种情况的原因分析如下。
由UKF滤波原理可知,该算法通过2n+1个采样点来近似非线性变化后的状态分布,其中n为状态方程维数。故在UNGM中,UKF算法每一时刻在f(x)中取3个采样点进行时间更新中一步预测值xk|k-1与方差Pk|k-1的计算。其中第一个采样点为上一时刻的状态估计值,另外2个采样点根据Unscented变换法则关于第一个采样点对称分布。假设某一时刻状态量位于平衡点附近,且估计值的绝对值与真实值接近,具体采样情况如图9所示。

图9 UKF采样情况示意图
由UNGM特性分析可知,当a取值较大且α取值较小时,平衡点距离y轴较远,如图9中的x1,此时3个采样点均位于同一象限。在这种情况下,当UKF发生模态判断错误,即估计值与真实值处于不同象限时,由于f(x)关于原点对称,UKF在估计值邻域进行的采样仍能很好地近似真实值邻域内f(x)区段对状态分布的影响。
但是当a取值较小且α取值较大时,f(x)沿y轴上下移动会使得某些时刻的平衡点距离y轴很近,如图9中的x2。此时,3个采样点将位于原点邻域内的不同象限。由于f(x)在原点附近快速震荡的特性,UKF采样点的分布将发生畸变,不再能够近似真实值邻域内f(x)区段对状态分布的影响。在这种情况下,即使模态判断正确,UKF仍会估计失准,且状态估计方差发散。具体情况如图10所示。
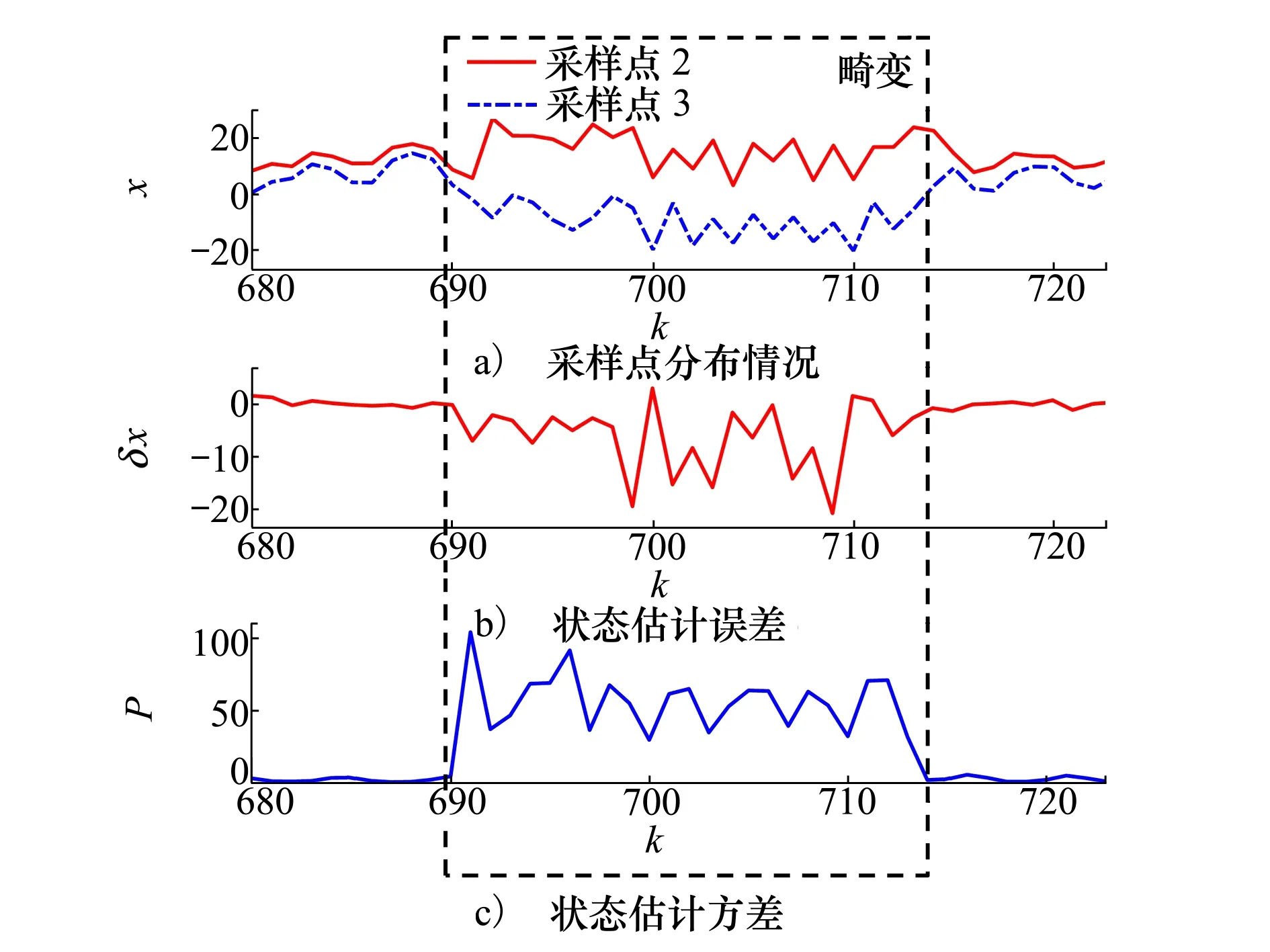
图10 状态估计方差发散时的UKF估计情况
由上述分析可知,第二类状态估计失准情况在任何确定性采样滤波器(UKF、CKF等)的估计过程中均会发生。即使在此类滤波器基础上做出算法优化,只要未改变采样法则,都无法避免此类情况的发生。
由卡尔曼滤波基本原理[22]可知,滤波的目的在于融合状态量与观测量的信息,使得滤波结果的方差小于系统噪声方差与观测噪声方差,以得到更为精确的估计值。故当滤波器估计值的方差无法收敛时,滤波器处于失效状态,估计结果不可靠。
文献[6,16]将优化后的UKF与UKF应用于本节参数设置条件下的UNMG,用以比较两者性能。由上述分析可知,在这种参数设置状态下,优化后的UKF与UKF均处于失效状态,而在滤波器失效时对其估计精度进行比较是缺乏意义的。
3 SSUKF算法设计
由UKF失准情况的分析可知,UKF不适合作为使用UNGM对非线性滤波器进行性能评估时的基准滤波器。为解决这一问题,本文提出具有滑动采样模块的UKF(UKF with sliding sampling module,SSUKF),具体设计如下。
3.1 修正模态判断错误
由UNGM特性分析可知,当α≠0时,状态量后验概率分布的双峰将失去对称性,本文将从这一特性着手进行研究。
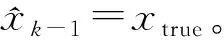
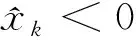
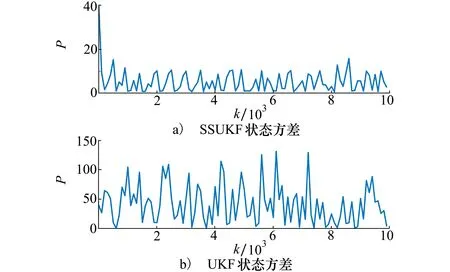
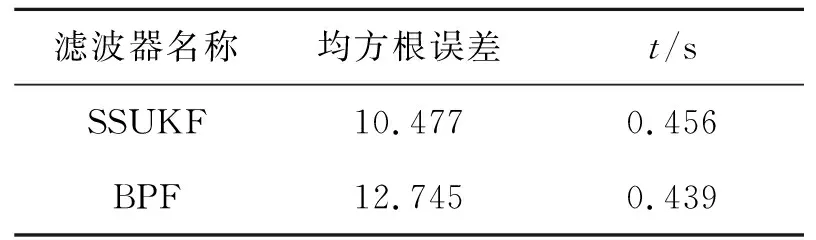
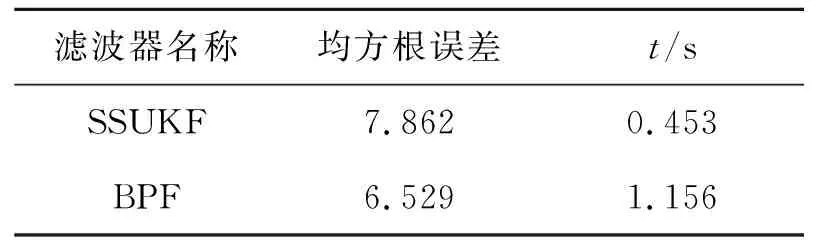
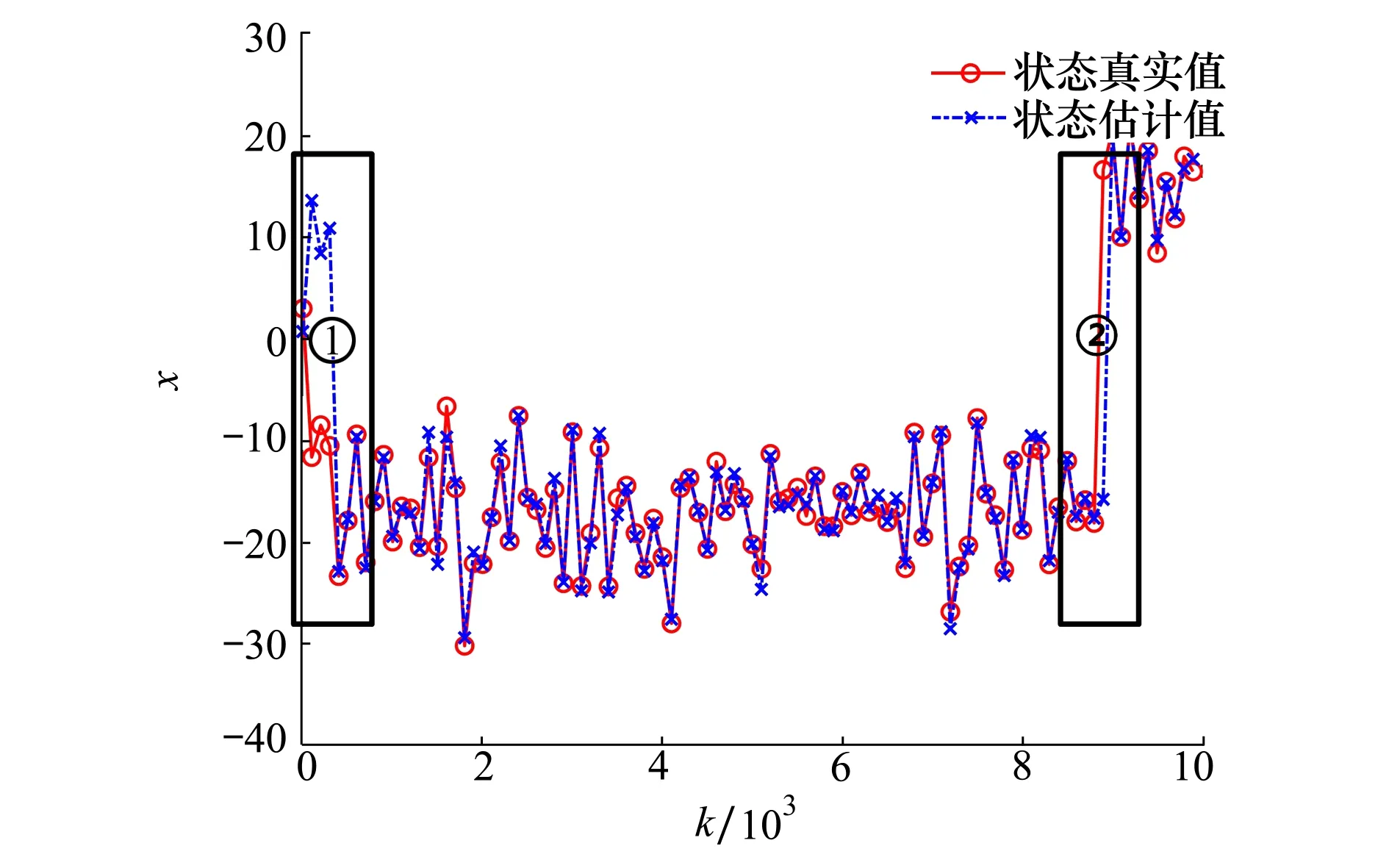
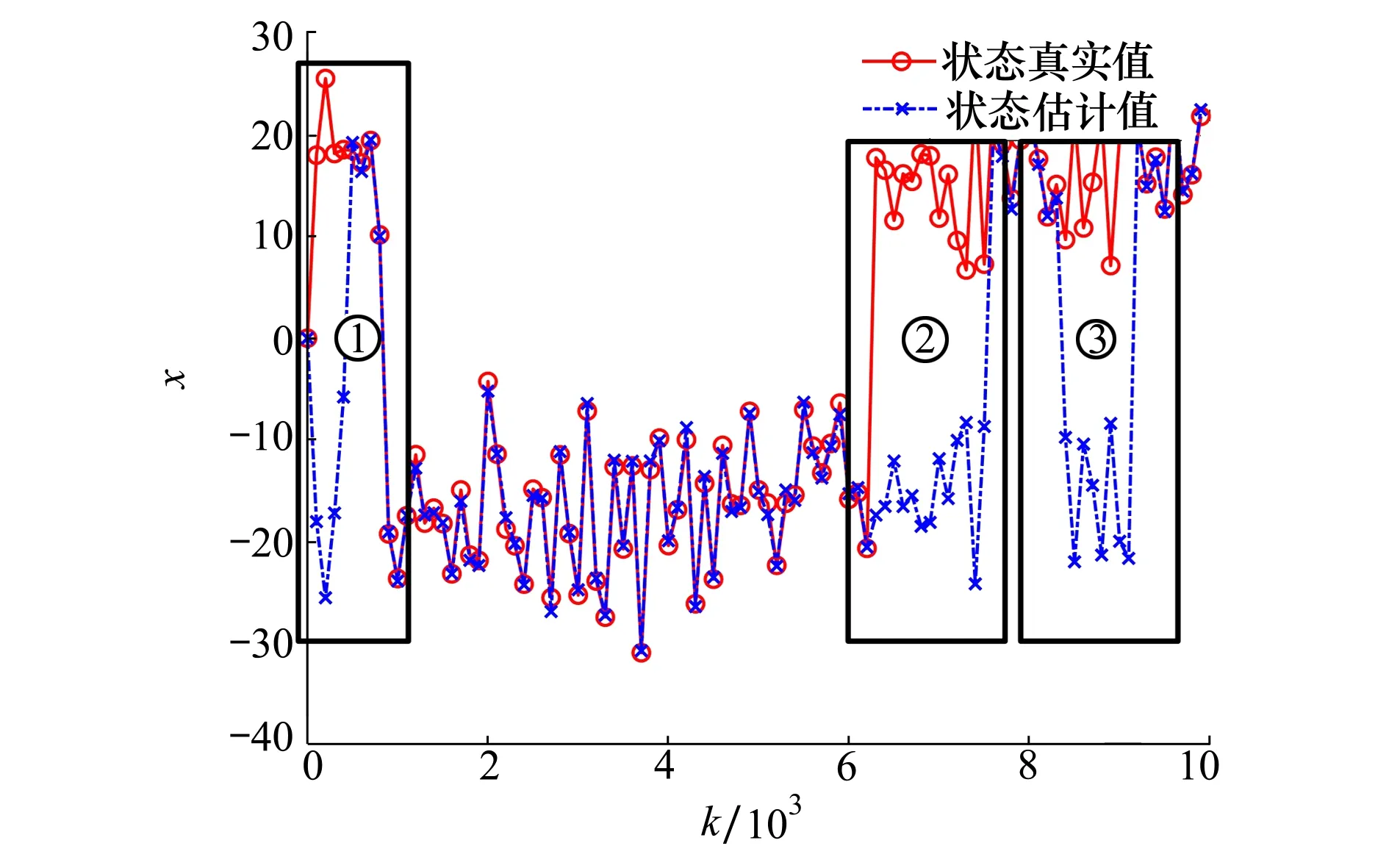
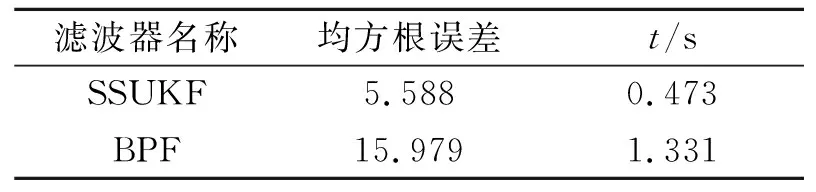
状态方程中cos(β(k-1))在同一时刻大小、符号相同,由于系统噪声w服从均值为0的正态分布,故此时xtrue 当估计值与真实值正负异号时,下一步真实值与滤波器一步预测值分别为 在这种情况下引入系统噪声w后,xtrue 需要注意的是,当选取样本点的阈值,即αcos(β(k-1))的大小确定时,α的值越大,在一定时间范围内,满足阈值被选取的时刻点k越多,反之则越少;采样数量n越小,对于模态错误的判断越迅速,但可能发生误判;n越大,对模态错误的判断的延迟越长,但判断结果也越准确。 本文在UKF的基础上对Sigma点采样法则进行修正,以解决状态估计方差发散的问题,方案如下。 为进一步验证SSUKF应对UNGM复杂特性的有效性,本文将SSUKF与UKF、BPF进行了仿真对比分析。 使用均方根误差(root mean square error,RMSE)来定量比较各滤波算法的精度。状态x在整个滤波时段的RMSE可以表示为 (7) 式中:x和xi分别为第i步时状态量的估计值与真实值;k表示滤波总步数。SSUKF与UKF的仿真结果对比如表1和图11所示。 图11 SSUKF与UKF的状态方差对比 表1 滤波器性能对比 由表1和图11可知,与UKF相比,SSUKF在计算时间基本一致的情况下,状态方差的收敛性与滤波精度都有较大提升。 已知BPF算法粒子数量多、分布范围广,能够较为有效地处理UNGM问题。基于BPF的各种优化滤波算法也经常使用UNGM进行性能评估。本文通过2组不同参数设置的UNGM,对BPF与SSUKF进行比较分析,以进一步评估SSUKF的性能(BPF算法详见文献[5],本文不再赘述)。 1) 第一组参数设置 令a=0.7,b=25,c=20,α=4,β=1.2。SSUKF采样数n=8,BPF粒子数为300。SSUKF与BPF的估计结果如图12~13所示。 图12 SSUKF的状态估计情况1 图13 BPF的状态估计情况1 由图可知,在这种参数设置条件下,状态量在正负平衡点之间的跳变较为频繁,SSUKF与BPF仍基本能够对状态量的变化进行跟踪。此时很难从图中直观评价滤波器性能好坏。滤波器性能的定量比较如表2所示。 表2 滤波器性能对比 由表可知,在这种参数设置条件下,BPF的估计精度略优于SSUKF,但SSUKF的计算时间明显小于BPF,此时2种滤波器性能接近。 2) 第二组参数设置 令a=0.9,α=1,β=0.4;由第3节分析可知,由于a变大,状态量模态跳变频次降低,故此时可以通过增加SSUKF采样点的数量以提高其模态判断的准确性,令n=100,其余参数不变。SSUKF与BPF的估计结果如图14~15所示。 图14 SSUKF的状态估计情况2 由图14可知,SSUKF在区域①发生初始模态判断错误;UNGM模型在区域②中因系统噪声而发生模态跳变。上述情形包含了2.1节中所描述的造成UKF失准的两类模态判断错误情况。当这两类模态误判发生时,SSUKF均正确做出判断并迅速修正。 由图15可知,BPF在区域①中迅速修正了模态判断错误;在区域②中则经过了较长的延迟才对模态错误做出修正;在区域③中则发生了模态误判的情况,估计值的符号发生错误跳变。这是由于当a较大时,UMGN后验概率密度的双峰分布间隔较大(详见UNGM特性分析),BPF的粒子分布稀疏使得采样信息充分,导致滤波器性能下降。这也体现了BPF对于具体模型针对性不强的特点。 图15 BPF的状态估计情况2 滤波器性能的定量比较如表3所示。 表3 滤波器性能对比 由上述分析可知,在这种参数条件下,SSUKF在模态判断准确性以及模态修正速度上均优于BPF。 由仿真结果可知,SSUKF在状态方差的收敛性与滤波精度上均优于UKF。此外,SSUKF可以根据模型特性的变化进行对应的参数调整。相较BPF,SSUKF的模型针对性更强且计算量更小。 综上所述,SSUKF通过对UKF自身滤波数据的充分利用与适当处理,解决了UKF应用于UNGM时的失准问题,达到了较好的滤波效果。 1) 对非线性滤波器设计与研究过程中普遍使用的UNGM进行了详细的特性分析,分析了模型参数对于模型特性的影响及其双峰特性的成因; 2) 指出UKF应用于UNGM时失准的原因主要在于模态判断错误与采样点畸变引起的方差发散,同时结合上述原因分析了在以往研究中使用UNGM与UKF时的不当之处; 3) 提出了SSUKF,仿真结果表明SSUKF能够有效解决UKF应用于UNGM时的失准问题。在使用UNGM对滤波器性能进行评估时,SSUKF弥补了UKF作为基准滤波器时论证不严谨的问题,更适合与各种非线性滤波器进行比较分析; 4) SSUKF在模态跳变的响应速度与模态判断准确性的兼顾层面仍有改进空间; 5) 如何将SSUKF的模态判断方法应用于实际工程模型中,有待进一步深入研究。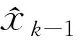
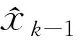
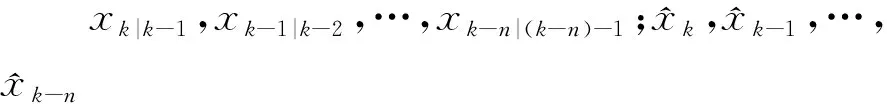
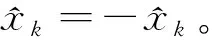
3.2 修正状态估计方差发散
4 仿真校验
4.1 SSUKF与UKF的仿真比较
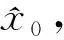
4.2 SSUKF与BPF的仿真比较


4.3 仿真总结
5 结 论

