考虑阻力发散约束的机翼气动/结构多点优化设计

张煜, 白俊强,2, 屈峰

(1.西北工业大学 航空学院, 陕西 西安 710072; 2.西北工业大学 无人系统技术研究院, 陕西 西安 710072)

大多数的航空公司更倾向于当前飞行器能够以至多1%的额外燃油消耗为代价,在比巡航马赫数更高的飞行马赫数条件下更为快速地完成飞行任务[1],这对于提升飞行器的经济性能具有重要意义。但自由来流马赫数逐渐提高时,受空气压缩性影响而产生的强激波会使得飞行器的阻力系数急剧增大,飞行器的气动性能和安全性能会随之恶化。针对该问题,有必要对飞行器巡航马赫数附近较宽速域内的阻力性能进行研究,推迟强激波的产生,即对飞行器的阻力发散性能进行研究。

为了获得良好的阻力发散特性,使得飞行器在巡航状态附近较宽的飞行速域内保持良好的气动性能,国内外的学者在该领域开展了广泛的研究。Kenway等[2]对CRM(common research model)构型的单独机翼进行了多点优化,得到了更加稳定的阻力发散特性。Tao等[3]使用改进的粒子群优化算法对某翼身组合体机翼的阻力发散性能进行了优化。陈迎春等[4]综述了中国大型客机空气动力设计过程,将空气动力设计定位为“突出巡航特性,重视设计鲁棒性”,对设计鲁棒性、非设计点特性和起飞着陆性能等提出了明确、周全、具有竞争力的指标。基于此思想,韩忠华、薛帮猛和黄江涛等[5-7]分别利用代理模型优化方法、遗传优化方法和离散伴随优化方法对大型宽体客机全机构型的机翼外形开展了包括阻力发散特性在内的多目标气动优化设计。

然而,考虑到静气动弹性效应的存在,飞行器在不同设计点下的实际气动外形均有所不同。如果仅从气动学科对飞行器的阻力发散特性进行约束,最终的设计效果会有一定损失。雷锐午等[8]的研究还指出,相比于“先气动后结构”的串行优化设计方法,并行气动/结构优化设计方法可以在同等阻力水平前提下获得更高的结构质量收益。因此,为了得到工程实用的设计结果,需要考虑静气动弹性影响,采用并行优化方法同时设计飞行器多状态的气动性能和结构性能,即对飞行器进行多点气动/结构鲁棒性设计。

相较于单学科单状态问题,考虑静气动弹性影响的气动/结构多点优化问题设计空间增大,设计变量增多,计算量加大,对于优化设计方法的设计效率及鲁棒性提出了较为苛刻的要求。面对此类问题,传统的无梯度类优化算法如基于群体智能的进化类算法等,将会消耗大量计算资源,收敛速度难以满足设计人员需求。梯度类算法的显著效率优势使其渐渐成为此类问题的首要选择。但对于气动/结构优化设计问题,单次耦合求解计算量较大,使用有限差分法求解梯度信息会使得计算量随设计变量个数增加而急剧加大,这对于具有大规模设计变量的优化问题并不适用。伴随方程法的出现很好地解决了大规模设计变量优化中梯度求解效率低的问题,使得梯度类优化算法真正成为高效实用的方法。该方法在20世纪90年代被Jameson[9]引入飞行器气动外形优化设计中,而后Alonso和Martins等[10-11]将伴随方法成功应用于气动/结构优化设计中。白俊强等[12]对伴随理论的优化方法在大型民用客机气动设计中的研究进展进行了详细阐述。

本文以阻力发散性能为约束,使用基于离散伴随的梯度类优化设计方法对某远程宽体客机机翼/机身/平垂尾/发动机构型进行了气动/结构的机翼多点精细化设计。首先基于RANS方程建立了高可信度的气动/结构数值求解方法并对其进行了精度验证。而后基于离散伴随方法,以梯度类算法为驱动,耦合FFD(free form deform)参数化方法和混合动网格算法搭建了可处理大规模设计变量及设计约束的气动/结构优化平台。最终利用该平台对所选取的研究对象进行了气动/结构多点优化设计,希望能够为大型民机多学科精细化设计提供有价值的技术和应用参考。

1 数值求解方法

本文采用基于RANS方程的开源流场求解工具ADflow[13]求解气动载荷。CFD(computational fluid dynamics)数值求解过程中采用多块结构网格、SA(spalart-allmaras)湍流模型进行全湍模式计算。该求解器基于离散伴随方法耦合了自动微分工具,可高效快捷地提供设计过程中流场变量的梯度信息。

结构变形由开源结构求解器TACS[14]求解。TACS包含静力分析、屈曲分析、非线性分析等模块,其基于二维有限元模型并行求解,可以很快地得到结构网格单元节点上的位移、应力和应变。该求解器同样耦合伴随方法实现了对结构状态变量的梯度信息的高效求解。

如图1所示,本文使用紧耦合迭代策略,CFD和CSM(computational structural mechanics)求解器在单个时间步内各自独立,依次交替求解,各学科计算在未收敛之前即进行数据交换。该方法气动学科与结构学科可以实时交换数据,求解效率高、精度高、计算资源消耗相对较少,但气动力和结构变形在还未收敛时就已经开始数据交换,稳定性可能会受到影响。为保证该方法的稳定性,设定单学科计算残差每降低10-1量级后才进行学科数据交换。

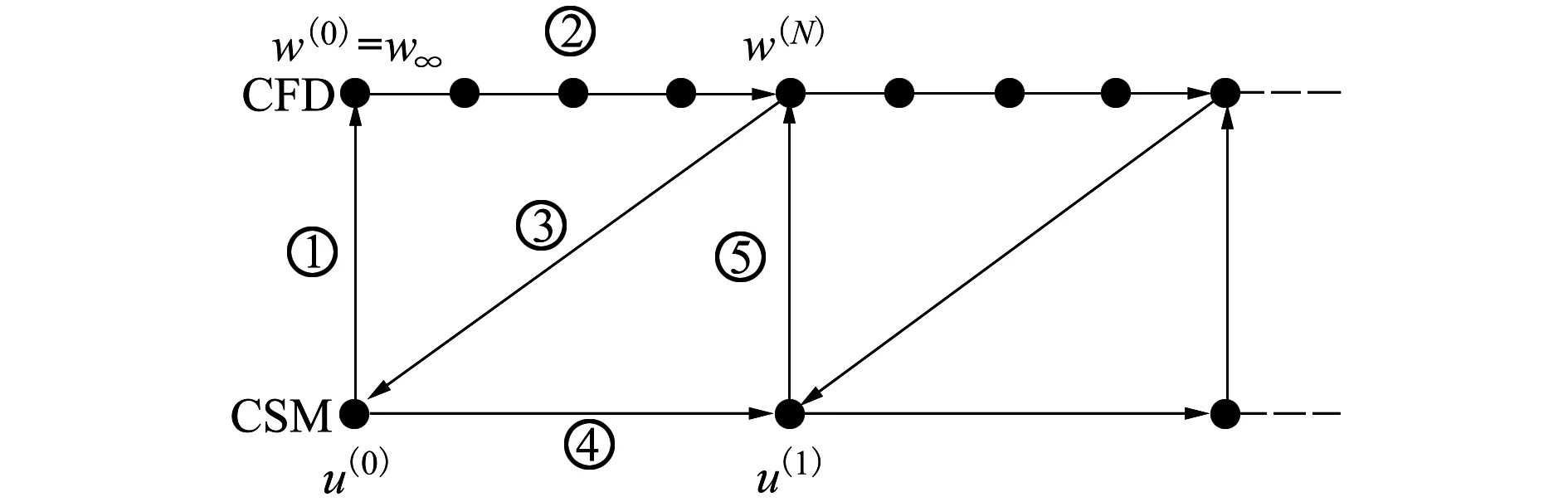
图1 气动/结构迭代流程

在学科模型迭代的过程中,本文使用RBF(radial basis function)插值技术[15]进行结构变形与气动载荷插值,采用虚功原理完成气动载荷数据交换。单次迭代数据交换完成之后,采用一种混合动网格技术[16]将气动物面网格的变化传递至空间网格。该方法将无限插值法与扭转弹簧法结合,基于分块结构网格的思想,每块结构网格的顶点变形由弹簧驱动,网格块内部的网格点根据顶点的位移采用无限插值法逐层插值得到。

为验证所建立的气动/结构耦合数值求解方法的准确性,本文选择DLR-F6翼身组合体构型[17]为测试对象,对比校验该构型在典型试验状态下机翼后缘展向挠度变形。试验状态为

Ma=0.75,Re=3×106,CL=0.50

计算过程中使用的气动网格及结构实体模型如图2所示。其中,气动网格量580万,结构有限元模型包括43 388个有限单元及37 665个节点,结构材料使用90MnV8钢。

图2 计算模型

考虑到当前气动/结构耦合数值求解方法使用的结构求解器TACS只能处理二维有限元模型,此次算例验证使用商业软件NASTRAN替代TACS进行结构实体模型计算分析。TACS求解器自身的精度已在文献[14]中进行过验证。采用NASTRAN进行气动/结构耦合数值求解方法验证,可以在一定程度上验证本文所采用的耦合策略、数据交换方法和动网格技术的可行性。

如图3所示,将当前数值计算结果与文献[18]仿真结果和NASA NTF(national transonic facility)风洞试验结果[19]进行对比。可以看出,三者的机翼后缘展向挠度变形分布规律较为接近,这说明当前所采用的耦合策略、数据交换方法和动网格技术能够正确反映气动/结构耦合效应,具有一定的可信性。也从侧面说明了本文建立的气动/结构耦合数值求解方法可以为优化设计提供较为可靠的计算结果。

图3 机翼后缘展向挠度变形对比

2 优化设计方法

本文建立的优化设计平台主要由以下系统构成:基于NURBS(non-uniform rational B-splines)基函数的FFD外形参数化[20]模块,混合算法网格变形模块,气动/结构耦合分析模块,伴随方程梯度求解模块和梯度类优化算法模块。具体设计流程如图4所示,在进行优化之前,需要事先建立气动学科模型、结构学科模型,而后在每一轮优化设计中,优化算法产生设计变量并传递给外形参数化模块。参数化模块对当前几何外形进行扰动,产生新的物面网格,而后动网格模块更新空间网格。至此气动学科模型与结构学科模型都得到了更新。然后进行气动/结构耦合分析,得到所需要的目标函数值。梯度求解模块则在收敛解的基础上求解伴随方程,组装各模块梯度信息,获得目标函数对于设计变量的导数。将目标函数值和导数值传递给优化算法后就可以获得新一轮的设计变量。

图4 优化设计流程

在优化算法模块中,使用SLSQP(sequential least squares quadratic programming)算法[21]更新设计变量。在梯度求解模块中,本文采用的学科求解器ADflow和TACS耦合了离散伴随方法,可以高效求解各自学科内的梯度信息。但对于学科间的耦合梯度信息,需使用自动微分工具处理学科数据交换代码,然后基于链式法则组装各模块梯度信息。

3 学科模型前处理

3.1 气动学科模型

气动学科模型由CRM构型[1]为基准设计得到,设计状态为

Ma=0.85,H=11.5 km,CL=0.48

该构型机翼前缘后掠角为35°,展弦比10.5,KINK位置在34.9%展长处。设计过程中使用的CFD网格规模在1 200万左右,如图5所示。

图5 机翼/机身/平垂尾/发动机构型气动网格示意图

图6a)展示了基础构型在设计状态下的机翼上表面压力云图,本文按展向位置等比例选取图中包括翼根、KINK及翼梢在内的10个翼型控制剖面进行了手动修型设计,初步调整了各控制剖面的几何扭转、翼型厚度和翼型压力分布,以保证基础构型机翼满足初始几何设计约束,如翼型厚度约束和机翼油箱容积约束等,同时气动性能不会过度恶化。图6b)则给出了其中4个控制剖面的翼型和压力分布,可以看出所设计的基础构型在设计状态有较好的气动性能,机翼压力分布形态和激波强度沿展向位置变化具有典型的超临界特征。

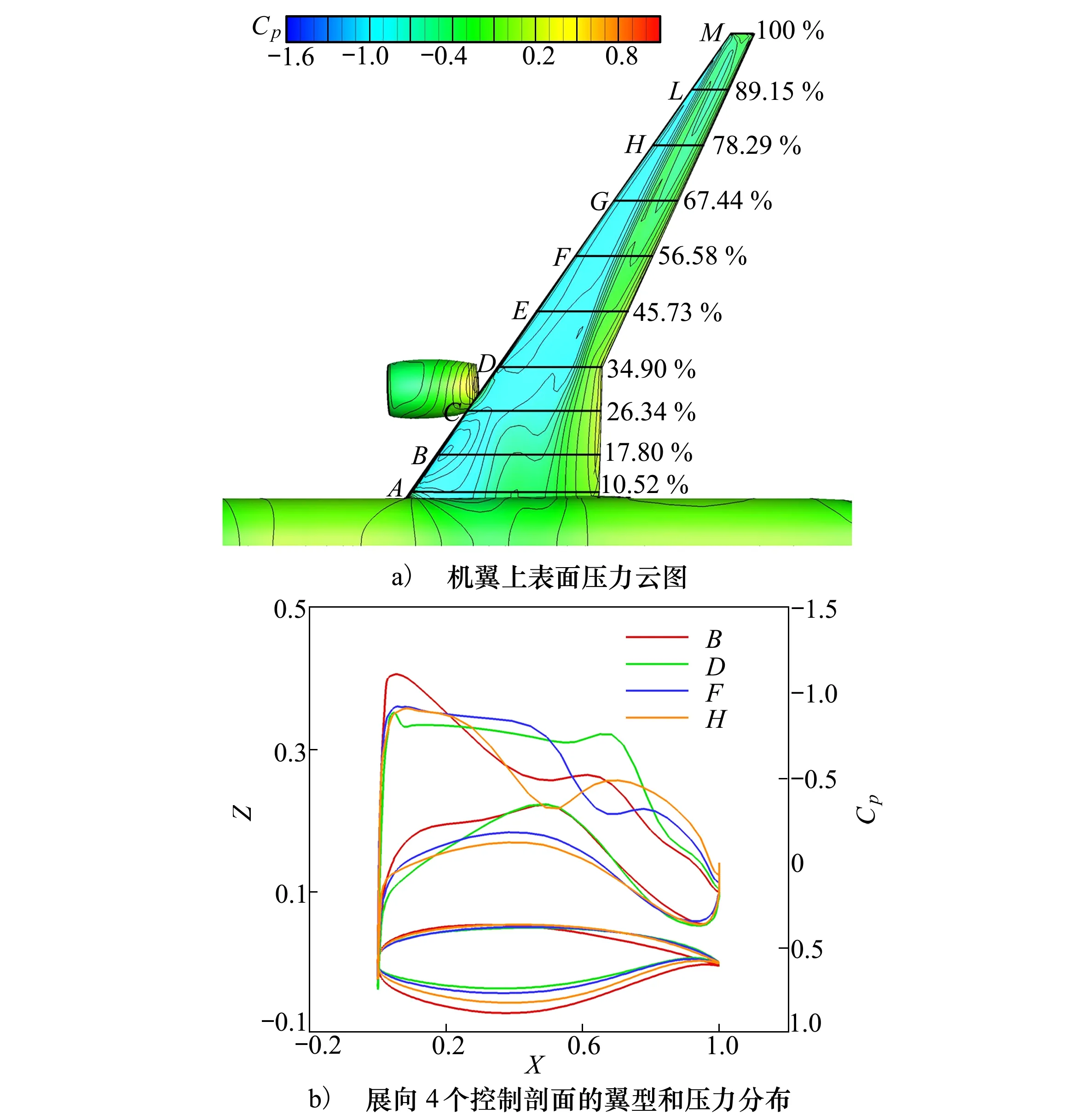
图6 基础构型气动性能

3.2 结构学科模型

机翼是构型飞行过程中产生升力的主要部件,为简化设计模型,本文在设计过程中只对机翼进行了结构布置,计算分析时只考虑该位置的弹性变形,机身、平垂尾等其余部件保持刚性。

结构学科模型中布置的翼盒结构及其约束如图7所示。该翼盒结构包括前后翼梁、翼肋、桁条和上下蒙皮,采用混合方式布置翼肋,中央翼盒顺气流方向布置翼肋,机身外翼盒垂直于前梁轴线正交布置翼肋,其中前梁轴线定义为翼根翼梢2处前梁位置连线。中央翼盒属于机身的一部分,用于提供与外翼的连接,并可以作为整体油箱使用。为模仿实际翼盒装夹,在对称面处翼肋施以固支约束,限制各方向自由度。翼根处翼肋将其X方向位移及Z方向位移限制为0,其余自由度不受限制。

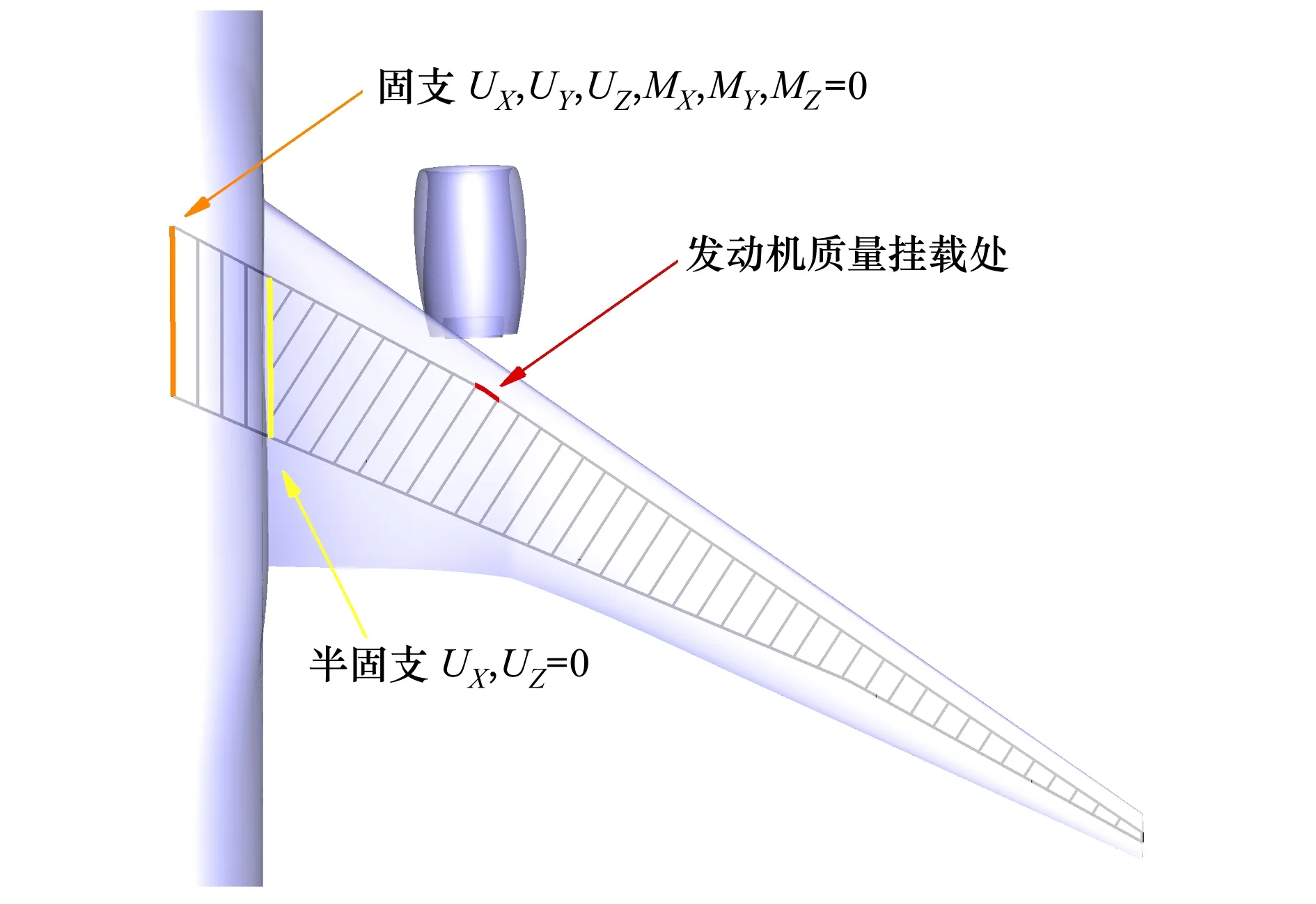
图7 翼盒结构布置

除了翼盒结构质量,设计过程中还考虑了翼盒燃油质量和发动机质量。其中,翼盒燃油质量均布于翼盒下蒙皮上,参考远程宽体客机波音787的飞行数据[22]将其设为40 t。本文所涉及的飞行状态均在巡航状态附近,设计过程中取燃油使用系数为0.5。发动机质量加载至如图7所示前梁处红色实线位置,参考GE90系列发动机质量,将该部分质量取为8 t。

机翼的所有结构部件,包括翼梁、翼肋、桁条和蒙皮,均由四节点线性壳单元构建,共93 952个有限单元。为便于研究,所有结构有限单元均使用高强度2024硬铝合金进行计算分析。

4 机翼气动/结构多点设计

本文主要对构型机翼的巡航性能及阻力发散性能进行设计。如表1所示,在巡航马赫数附近选取3个设计状态,通过多点多目标优化设计保证设计结果鲁棒性。所有设计状态构型飞行高度均为11.5 km。

表1 设计状态

4.1 设计目标

气动学科优化目标为减小各设计状态的阻力系数CDi,结构学科优化目标为减小翼盒结构质量M。受SLSQP算法限制,使用加权和法将各学科目标函数转化为一个加权目标函数

f=λ1×∑wiCDi+λ2×M,i=A,B,C

式中,λ1和λ2为学科权重系数,本文基于文献[23]中对气动/结构目标函数设定的研究,结合设计需求,假定气动学科1 count的阻力收益等同于结构学科100 kg质量收益,取λ1/λ2=1×106;wi为气动学科子权重系数,为突出巡航状态减阻效果,将设计状态A,B,C子权重系数比例wA∶wB∶wC取为1∶3∶1。

4.2 设计变量

本文考虑的优化问题的设计变量包括:几何设计变量、气动设计变量以及结构设计变量。

首先介绍几何设计变量。使用FFD参数化方法将基础构型参数化,建立如图8所示FFD控制框。机翼控制框(图8中黄色圆点)共布置300个控制点,用于控制机翼几何型面变化以及几何扭转角变化,结构模型各部件也会随着机翼几何型面的变化而变化。控制点均匀分布在展向10个控制剖面,每个控制面上下沿弦向布置15个控制点,优化过程中提供控制点Z向位移即可改变对应位置机翼外形。机翼几何扭转角变化对应沿展向的10个控制剖面的扭转角变化,通过绕对应剖面机翼前缘Y轴的转动实现。

图8 FFD控制框

平尾控制框(图8中蓝色圆点)用于控制平尾整体偏转以实现全机力矩配平。平尾整体偏转通过FFD控制框绕给定转轴(图8中红色实线)旋转实现,其中给定转轴定义参考实际飞机平尾偏转,取为平尾翼根和翼梢40%弦向位置连线。设计时只考虑构型巡航状态B的力矩配平。

机身控制框、垂尾控制框和发动机控制框用于与机翼控制框和平尾控制框对接,从而在优化设计过程中保证各部件交接位置处原有几何连续性。

最终几何设计变量包括300个机翼FFD控制点Z向位移变量Zwing,10个机翼几何扭转角变量φwing和1个平尾扭转角变量φtail。

气动设计变量包括3个设计状态的来流迎角αi,优化时为保证设计状态不发生变化,需要不断调整来流迎角以满足定升力约束。

结构设计变量为各部件有限单元厚度Twing,其中,每个翼肋的厚度作为一个设计变量,每个桁条的厚度作为一个设计变量,前后梁每相邻2个翼肋之间部分的厚度作为一个设计变量,蒙皮被翼肋和桁条相互交替划分为多块,每块蒙皮的厚度作为一个设计变量。最终结构设计变量包括45个翼肋厚度变量,44个前梁厚度变量,41个后梁厚度变量,40个桁条厚度变量以及974个蒙皮厚度变量,共计1 144个设计变量,如图9所示,图中每个颜色不同的区域厚度即为一个结构设计变量。

图9 结构设计变量示意图

4.3 设计约束

本文考虑的优化问题的设计约束包括:几何设计约束、气动设计约束以及结构设计约束。

几何设计约束包括机翼厚度约束和控制剖面的前后缘约束。设计过程中为保证机翼装载空间不减小,必须对机翼厚度进行约束。在设计过程中加入了250个厚度约束,均匀分布在沿机翼展向的10个控制剖面,每个剖面沿弦向均布25个,限制每一个约束处的相对厚度Ti始终不小于基础构型初始厚度Ti0。同时为保证机翼FFD控制点Z向位移变化引起的物面变化不会改变当地机翼几何扭转角,使得FFD控制点设计变量Zwing与几何扭转角设计变量φwing相互独立,在机翼每个控制剖面加入前后缘约束,约束前后缘控制点Z向位移扰动量大小相等,方向相反。

气动设计约束包括3个设计状态的定升力约束以及巡航状态的力矩配平约束。此外,本文将阻力发散性能指标作为气动设计约束引入优化问题中。实际工程中一种较为常用的判断阻力发散特性好坏的方法是:在固定巡航升力系数的前提下,马赫数较巡航状态马赫数增加0.02时,其阻力系数差量是否小于20 counts(1 count=10-4),若小于,则当前构型具有较为良好的阻力发散特性。依据此种方法,并尝试进一步挖掘构型阻力发散性能潜力,本文约束巡航状态B与高马赫数计算状态C之间的阻力系数差量不大于19 counts。

结构设计约束为结构模型的93 952个有限单元的屈服强度约束。为保证设计过程中材料不发生损毁,优化过程中约束所有有限单元的屈服应力σyk小于所使用材料2024硬铝合金的屈服强度极限σy,2024,如下式所示

σy,2024=2.75×108Pa

式中:n为安全系数,对于本文所使用的2024硬铝合金,其极限强度与屈服强度之比约为1.5,故设计过程中取安全系数n为1.5。同时考虑到实际飞行器结构要求能够承受极限过载2.5g状态下载荷,设计过程中判断屈服应力是否满足约束时,统一将应力值放大2.5倍。

结构设计约束要求在不同计算状态下均满足屈服强度要求,故最终会增加93 952×3个约束。为提高设计效率,利用Kreisselmeier-Steinhauser(KS)凝聚函数[24]将每个设计状态下翼肋所有结构设计约束、翼梁所有设计约束、桁条和蒙皮所有设计约束各自聚合,得到9个结构屈服强度约束函数KSi,ribs、KSi,spars和KSi,stringers & skins。凝聚函数方法通过构造光滑函数一致逼近最大值函数,将大规模的设计约束凝聚为一个或多个函数,可有效降低算法寻优工作量。

4.4 优化模型

考虑前述所有设计目标、设计变量和设计约束,最终优化模型如表2所示。当前优化问题共包括1个加权目标函数、1 458个设计变量、284个设计约束。对于传统的进化类优化方法或基于有限差分的梯度类算法来说,这样的气动/结构多点优化设计问题是一个不小的挑战。

表2 优化模型

4.5 设计结果

使用国家超级计算天津中心主频为2.93 GHz的560个计算核心对该远程宽体客机构型进行了优化,前后耗时约两周。同时,为了对比机翼气动/结构多点优化性能,文中额外加入了气动学科巡航单点优化算例和结构学科巡航单点优化算例。其中,气动学科单点优化以巡航阻力系数为优化目标,不考虑结构有限元厚度变量、结构屈服强度约束和阻力发散约束,基于气动求解器ADflow对该构型气动外形进行了优化;结构学科单点优化以结构质量为优化目标,仅考虑结构有限元厚度变量和结构屈服强度约束,以初始构型巡航气动力为外载荷,基于结构求解器TACS对该构型结构尺寸进行了优化。

基础构型、气动学科巡航单点优化结果与气动/结构多点优化结果的气动力系数对比如表3所示。在满足各计算状态定升力约束以及巡航状态力矩自配平约束的前提下,气动/结构多点优化构型在低马赫数状态A的阻力系数减小1.75 counts,巡航状态B的阻力系数减小13.67 counts,高马赫数状态C的阻力系数减小23.21 counts,各状态升阻性能均有所提升。气动单点优化构型虽然在巡航性能上略优于多点优化构型,但在非设计点阻力性能恶化,构型鲁棒性减弱。

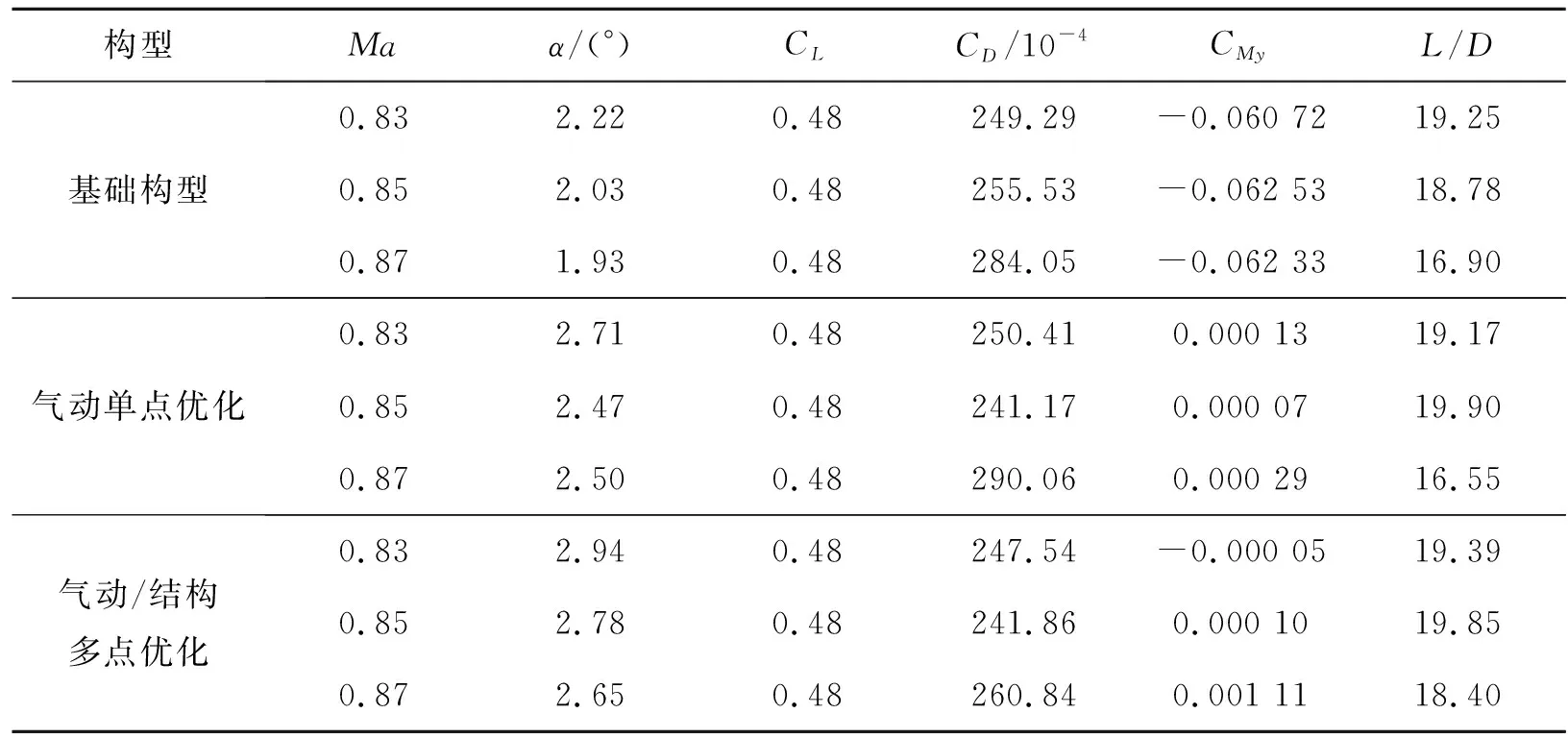
表3 气动力系数对比

进一步对比构型阻力发散特性,图10给出了各构型阻力系数随马赫数变化曲线。优化后,气动/结构多点优化构型0.87Ma较0.85Ma阻力系数差量由28.52 counts减小至18.98 counts,满足优化问题设置的阻力差量不大于19 counts的约束,构型阻力发散特性得到改善。气动单点优化构型0.87Ma的阻力系数急剧增加,与巡航状态的阻力差量增至48.89 counts,阻力发散性能变差。这说明大型客机空气动力设计过程中需要综合考虑构型包括巡航状态在内的多个设计状态的气动性能,单点设计虽然可以在单一设计状态下获得较优性能,但其他设计状态的气动性能可能会因此恶化。

图10 阻力系数随马赫数变化曲线

基础构型与气动/结构多点优化构型巡航状态气动性能的详细对比如图11所示。图中从上至下、从左至右依次展示了两构型之间的气动力系数、上表面压力云图、激波区域、机翼展向载荷、机翼几何扭转角分布、机翼展向厚度分布、各剖面翼型和对应压力分布。可以看出,在满足机翼厚度约束的前提下,优化构型激波区域大幅减小,机翼上表面等压线近似平行分布,激波阻力明显减少。对比各展向站位压力分布及翼型几何,优化构型各剖面翼型上翼面更加平坦,压力恢复均匀,部分翼型后缘弯度减少,机翼后加载也随之减小,为弥补部分升力损失,优化构型增加了机翼的前缘头部压力峰值。

另一方面,为减小诱导阻力,使机翼展向载荷分布趋于最佳环量分布,优化后构型机翼载荷外移,而外翼载荷的增加,造成了外翼展向挠度变形增大,外翼各展向站位翼型相对位置发生较大变化。受气动弹性变形的影响,机翼各站位几何负扭转均有所增加,外翼由于载荷外移,这种变化更为明显。为了满足定升力约束,弥补机翼几何负扭转增加造成的升力损失,构型在各计算状态下来流迎角均有所增加。对比各构型各计算状态来流迎角,如表3所示,多点构型最大增量为0.75°,位于巡航状态。单点优化构型各计算状态下的来流迎角也有所增加,但巡航状态的来流迎角增量仅为0.44°。这说明设计过程中气动弹性变形的存在会驱使飞行状态的来流迎角增加以弥补后掠翼几何负扭转增加造成的升力损失。如果需要维持与基础构型相当的来流迎角,后续设计过程中可调整机翼安装角或加入迎角约束对当前构型重新进行优化。

图12给出了3个计算状态下气动/结构多点优化构型部分剖面的压力系数分布对比。本文给予了巡航状态B较大的子权重系数,设计过程中优化算法更倾向于提升B状态的气动性能。故相较于其他计算状态,B状态气动性能提升较为明显,展向各站位压力分布不存在较大逆压梯度。而低马赫数计算状态A的中、外翼部分区域前缘出现较大逆压梯度,高马赫数计算状态C的大逆压梯度则出现在后缘,这说明该优化构型在A和C状态下仍有较大减阻潜力。但对于多点鲁棒性优化设计,要求每个设计状态的机翼压力分布均光滑过渡以获得最优气动性能是较为困难的,实际设计过程中需要设计人员对各状态性能进行权衡取舍。

图12 3个计算状态下气动/结构多点优化构型部分剖面的压力系数分布对比

气动单点优化构型与气动/结构多点优化构型巡航状态的部分气动性能对比如图13所示。图中展示了两构型之间的气动力系数、上表面压力云图和部分典型剖面的翼型几何及压力分布。这两构型巡航状态的气动性能相近,各位置激波强度较基础构型均得到减弱,中翼段基本无激波。气动单点优化构型内翼段前缘峰值略低,外翼段激波位置相对靠前。

图14给出了结构单点优化结果与气动/结构多点优化结果的结构有限元模型厚度分布对比。在满足所有结构屈服强度约束的前提下,结构单点优化构型的结构质量为13 904.04 kg,气动/结构多点优化构型的结构质量为16 840.55 kg,二者质量相差2 936.51 kg。虽然气动/结构优化构型巡航状态的激波强度得到有效减弱,机翼应力集中区域减小,但在低马赫数状态A和高马赫数状态C下机翼前后缘出现的大逆压梯度区域对翼盒结构提出了新的强度要求。此外,优化构型各状态机翼压力分布前缘头部峰值的提高也增加了机翼前缘的应力值。在这些因素综合影响下,气动/结构多点优化构型的翼盒结构弦向中部高厚度区域向前后缘延伸,机翼质量增加,结构鲁棒性增强。

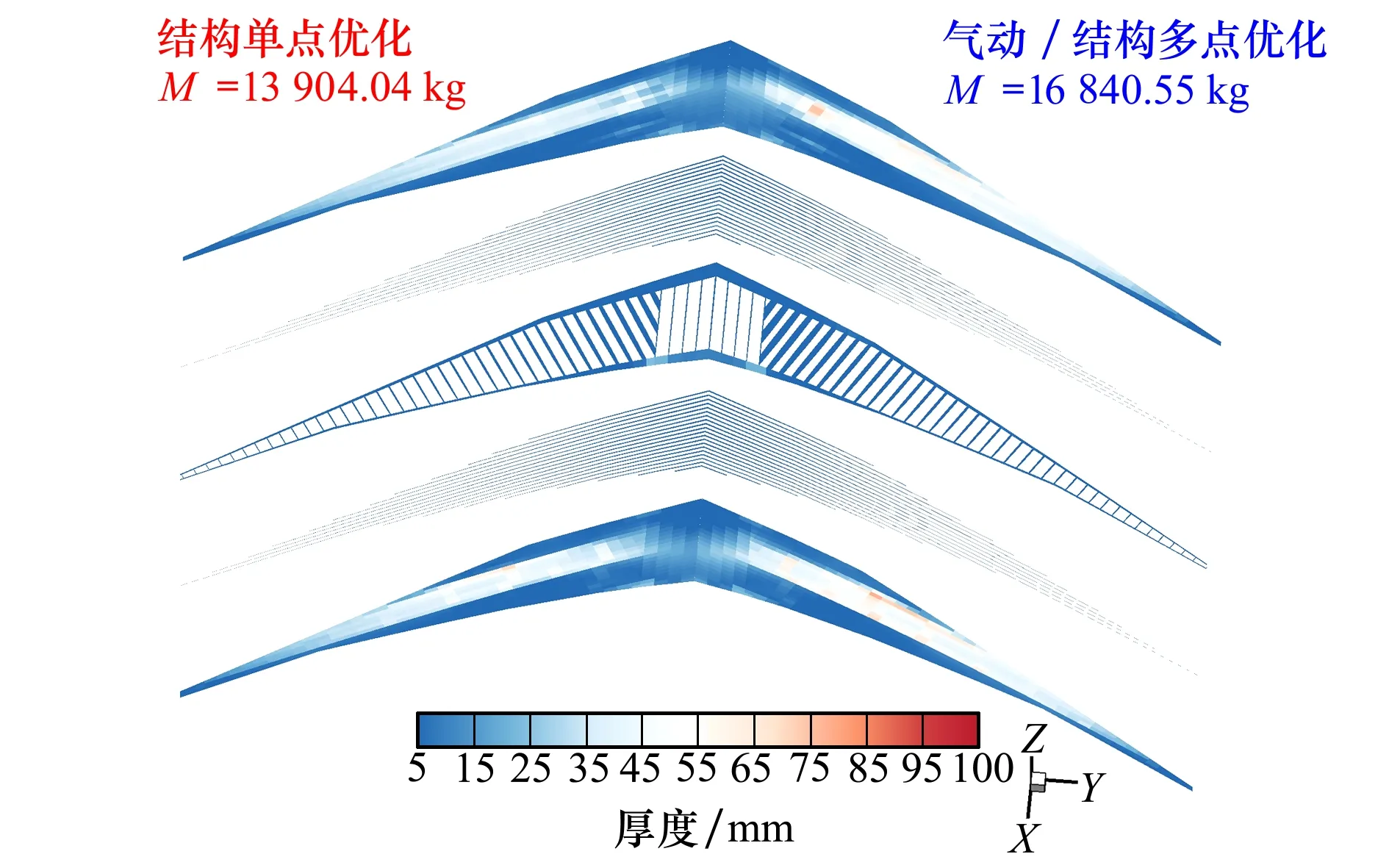
图14 结构单点优化构型与气动/结构多点优化构型的结构有限元模型厚度分布对比

5 结 论

本文以阻力发散性能为约束指标,使用基于离散伴随的梯度类优化设计方法对某远程宽体客机机翼/机身/平垂尾/发动机构型进行了气动/结构的机翼多点精细化设计。

1) 利用DLR-F6翼身组合体构型对建立的气动/结构耦合数值求解方法进行了验证。结果表明该数值求解方法能够正确反映气动/结构耦合效应,可以为优化设计提供较为可靠的计算结果。

2) 优化结果各设计状态的阻力系数均有所减小,巡航状态阻力系数减小13.67 counts,0.87Ma设计状态较0.85Ma设计状态阻力系数差量由28.52 counts减至18.98 counts,飞行器阻力发散性能得到改善。其结构质量与结构巡航单点优化设计结果相比增加了2 936.51 kg,机翼弦向中部高厚度区域向前后缘延伸,结构鲁棒性增强。

3) 结构变形的存在导致后掠翼各位置出现几何负扭转,尤其是外翼段,进而驱使各飞行状态来流迎角增加以弥补升力损失。考虑气动/结构多学科的优化设计方法可预先加入安装角设计变量或来流迎角设计约束来维持与基础构型相当的来流迎角。

4) 多个设计状态的气动载荷会对结构模型的不同区域提出不同的强度要求。综合考虑构型包括巡航状态在内的多个设计状态的气动载荷可以使得结构模型各部件强度提高,鲁棒性增强,但结构质量会增加。

5) 相较于单学科单点设计问题,考虑阻力发散特性的气动/结构多点优化设计可以充分挖掘构型设计潜力,得到综合性能更好、工程实用性更强的设计结果。

6) 为减少问题复杂度,本文对结构学科模型进行了一定简化,仅对结构模型各部件的尺寸进行了优化。可以推论,结构学科仍然有较大的优化潜力,如果使用复合材料或结构拓扑优化等其他先进技术,可使得飞行器的综合性能获得进一步的提升。

致谢本文在研究过程中得到了商飞上海飞机设计研究院张淼、马涂亮等同志的指导和大力支持,在此表示衷心感谢。