从三个视角看幂的运算

王宪成

“幂的运算”是苏科版数学七（下）第8章的内容。在此之前，我们已经学习了“有理数”，知道了有理数的乘方运算的结果叫幂，还认识了幂的底数、指数、读法、性质，科学记数法，有理数的混合运算等。同学们，你们有没有思考过如下问题，比如幂是乘方运算的结果，也是一个数，可以进行加、减、乘、除、乘方等运算吗？幂的指数只能是正整数吗？等等。看来，我们有必要全面地认识本章内容，并站在前后知识联系、发展的角度来深入学习。

一、从数的运算视角看幂的运算

经历过小学数学运算，我们知道了，减法是加法的逆运算，除法是乘法的逆运算。在七年级上学期，我们学习了“有理数”。求相同因数积的运算叫作乘方，幂是乘方运算的结果，也是一个数，自然有同学会问：乘方的结果“幂”，可以继续进行加、减、乘、除、乘方运算吗？这是从数学内部角度进行的思考，值得重视。

同学们可以展开讨论，如24×23、（24）3、（2×3）3、24÷23、23÷24如何运算？我们从乘方运算的视角不难理解上述运算。可是为什么要重点研究同底数幂的运算呢？经历过不同底数幂的运算之后，我们会发现，同底数幂的运算更具有一般规律性，更便于表达，所以更有研究的价值。

从生活与数学的联系中，我们也能感受到研究幂的运算的必要性。本章的章头图里有这样几个问题，光在真空中的速度约是3×108m/s，光在真空中穿行一年的距离称为1光年，请你算算：（1）一光年约是多少千米（1年以3×107s计算）？（2）银河系的直径达10万光年，约是多少千米？（3）如果一架飞机的飞行速度为1000km/h，那么光的速度是这架飞机速度的多少倍？带着这些问题，我们将学习同底数幂的乘法、除法以及幂的乘方和积的乘方。

二、从数到式的发展视角看幂的运算

同学们已经知道，同底数幂的乘、除、乘方等运算更容易开展研究。那么，仍然以24×23、（24）3、（2×3）3、24÷23、23÷24这些幂的运算为例，我们能否将其进行一般化归纳呢？从特殊到一般，归纳表达一般性，这是我们常见的研究路径，也应该成为同学们的数学素养。于是，用字母表示数就自然产生了。从数到式的发展，合情合理，自然发生。同底数幂的乘法、幂的乘方、积的乘方、同底数幂的除法法则就出现了。基于乘方的意义，推理法则的形成过程，可以发展同学们的代数推理能力。

从整式的运算视角来看，我们在整式加减的基础上，又有了新的研究方向，即整式乘法如何运算。如a4b3⋅ab2、a4b3·（ab2-a2b）、（a+b）·（ab2+a2b）……这就有了“整式乘法与因式分解”的研究内容。这样，后续的学习就有了“根”。

三、从指数的变化视角看幂的运算

幂的指数难道就只能是正整数吗？显然不是。那么，负整数、零、分数都可以吗？有时，数学学习需要我们大胆地提出问题，大胆猜想，细心分析问题。

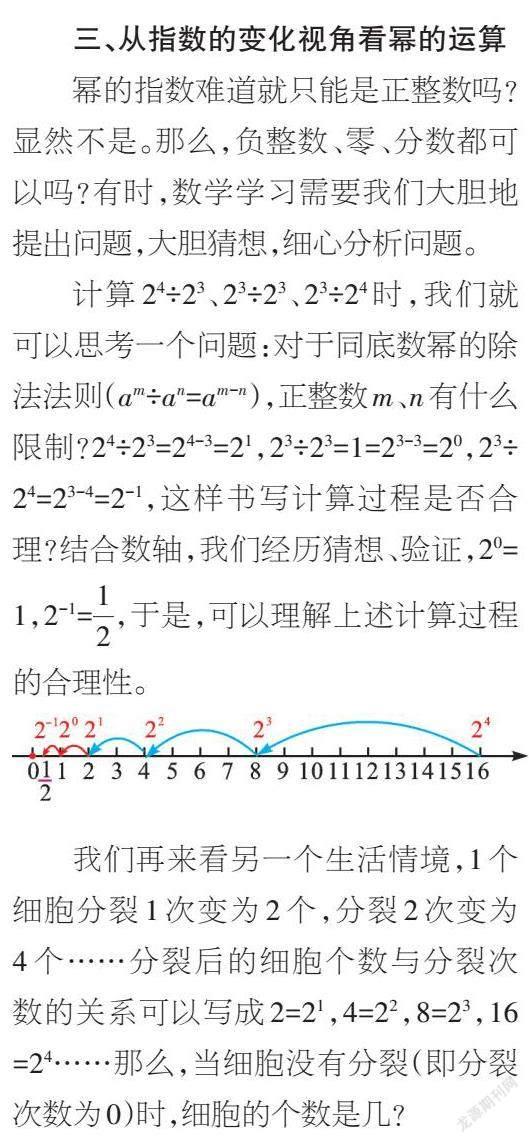
计算24÷23、23÷23、23÷24时，我们就可以思考一个问题：对于同底数幂的除法法则（am÷an=am-n），正整数m、n有什么限制？24÷23=24-3=21，23÷23=1=23-3=20，23÷24=23-4=2-1，这样书写计算过程是否合理？结合数轴，我们经历猜想、验证，20=1，2-1=[12]，于是，可以理解上述计算过程的合理性。

我们再来看另一个生活情境，1个细胞分裂1次变为2个，分裂2次变为4个……分裂后的细胞个数与分裂次数的关系可以写成2=21，4=22，8=23，16=24……那么，當细胞没有分裂（即分裂次数为0）时，细胞的个数是几？

于是，幂的指数进行了数的扩充，更加丰富了同学们对幂的认识。指数可以是正整数、0和负整数。有的同学会进一步大胆思考：指数有没有可能是分数呢？任意有理数呢？任意无理数呢？等等。随着同学们的不断追问，数学就这样自然“生长”起来了。

（作者单位：苏州工业园区青剑湖实验中学）