基于楔形体理论的市政管网超大直径钢顶管施工开挖面极限支护压力研究

梁 斌,房鹏帅,李文杰,耿 弈,唐 刚

(1.河南科技大学 土木工程学院,河南 洛阳 471023;2.中交二公局第四工程有限公司,河南 洛阳 471013)

0 引言

顶管法作为市政地下管道施工的重要工法,因其施工效率高、环境污染小等优点而得到了广泛应用。随着施工要求的提高,中小型顶管施工已难以应用于工程实践。近年来,超大直径钢顶管施工逐渐成为城市可持续发展的重要施工方法之一。但是随着顶管直径的增加,在施工应力作用下会加深土体扰动程度,引起开挖面土体异常移动,发生失稳破坏,产生地表沉降[1-5]。此外,超大直径钢顶管施工可供借鉴的资料非常有限,设计理念缺乏,并且由于其断面高度远大于中小型钢顶管,若采用传统分析方法研究其开挖面稳定性,结果的准确性难以保证,这无疑为超大直径钢顶管的安全施工带来了极大挑战。

近年来,关于隧道开挖面稳定性问题,诸多学者通过数值模拟、模型试验和理论解等方法对其进行研究。数值模拟的优势在于可以通过改变影响参数,模拟复杂地层在不同荷载条件下的各种施工工况,从而解决许多复杂的工程问题[6-11]。在模型试验方面,文献[12]通过模型试验研究了不同控制参数对竖向顶管施工的影响。文献[13]基于砂层护壁浆液室内试验,探讨了大直径顶管穿越沙漠深部浆液流变性、失水造壁性、润滑性的变化规律,但由于其受试验时间、费用等因素限制,难以应用于工程实践。文献[14]通过离心机试验模型对隧道开挖面支护压力进行研究,但没有对其失稳破坏模式进行归纳总结,缺乏相应的理论基础。

理论解因其严密的理论推导在工程界得到了应用,根据现有研究成果可将其分为极限平衡法和极限分析法。失稳破坏理论计算模型主要有：三维楔形体模型、对数螺旋模型和仓筒模型[15-20]。这些理论模型由于没有考虑土拱效应对开挖面稳定性的影响,计算出的理论解往往比实际工程偏大,部分学者通过改进计算模型,对考虑土拱效应展开了研究。文献[19]通过修正楔形体计算模型,推导出矩形顶管施工的主动极限支护压力的计算方法。文献[20]基于Terzaghi松动土压力理论,考虑顶管施工土拱效应的影响,揭示了滑移破裂面形态特征。理论分析法虽然可以获得开挖面极限支护压力,但是求解过程繁琐复杂,不便于实际工程应用。因此,面对日益复杂的钢顶管施工,有必要提出一种简单可行的开挖面极限支护压力计算方法,为超大直径钢顶管的安全施工提供必要的分析理论。

上述文献对管网施工开挖面稳定性研究主要集中在开挖面的破坏模式和对极限支护压力值的确定,但对极限破裂角和最大梯形底角的研究却鲜有报道,且缺乏合理的理论计算模型。本文采用有限元软件研究超大直径钢顶管施工开挖面破坏模式和机理,将传统的楔形体-棱柱体计算模型修正为楔形体-梯形体计算模型,推导出极限支护压力的计算公式。结合工程实例进行极限破裂角、梯形底角、土体内摩擦角、黏聚力和埋深直径比对极限支护压力影响的参数分析。本文提出的极限支护压力计算方法,可为超大直径钢顶管的设计与施工提供一定的理论基础。

1 泥水平衡钢顶管施工开挖面稳定性分析

1.1 工程概况

本项目为深圳市石岩北清污分流超大直径钢顶管工程,顶管管径D=4 m,壁厚30 mm,埋深C=10 m,始发井10座,接收井5座。根据石岩北工程地质勘察报告,该地区地质条件复杂多变,基本为第四系冲洪积层,地层主要以淤泥质土、砾质黏土、中粗砂和砂砾等为主,其中砂土地层稳定性能差、结构松散、黏聚力小。在超大直径钢顶管施工时,容易导致开挖面失稳,引起地层坍塌。数值模拟材料参数取值如表1所示。

表1 数值模拟材料参数取值

1.2 开挖面稳定性数值模型的建立

由于本文主要研究内容为顶管施工开挖面稳定性及极限支护压力的计算,故采取一次性开挖15 m模拟顶管施工过程。对于泥水平衡钢顶管,由良好“泥膜”形成的支护压力可以平衡开挖面水土压力,因此开挖完成后,在开挖面上施加与原始地层静止水土压力值(K0∑γihi=62.5 kPa)相等的均布支护压力[6,17]。由于浆液的润滑作用,忽略摩擦力对土体的影响,同时采用等代层法[21]模拟地层损失。为消除边界效应的影响,可以适当增大模型尺寸,建立泥水平衡超大直径钢顶管施工模型长、宽、高为45 m×40 m×25 m,其纵断面有限元模型如图1所示。

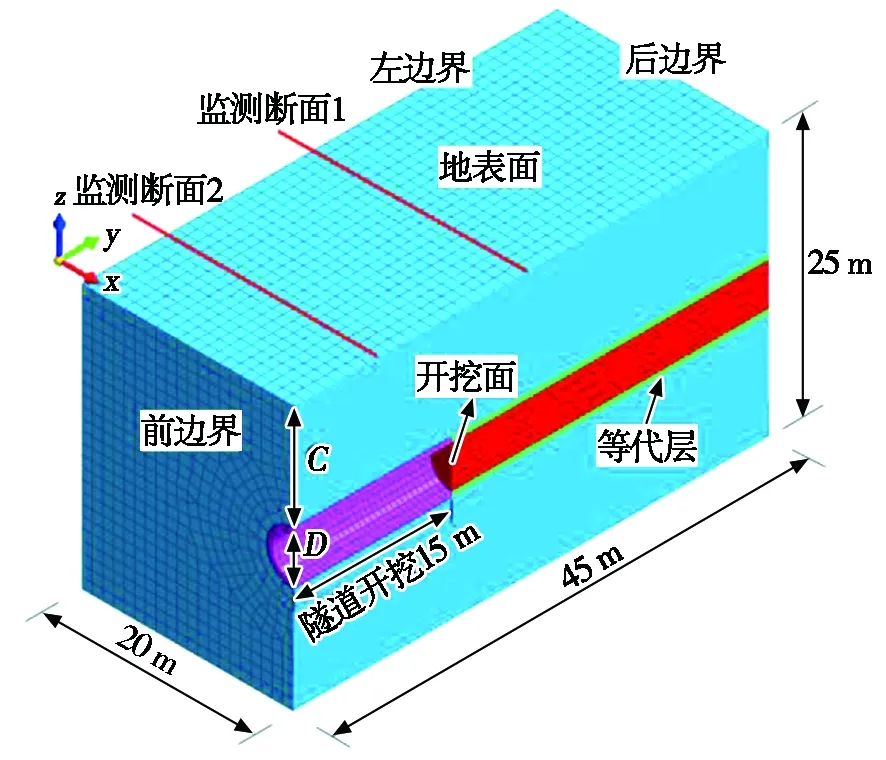
图1 超大直径钢顶管施工开挖面纵断面有限元模型

该模型中地表面设为自由边界,其他侧面的边界条件均为固定法向位移。在计算过程中土体材料的破坏屈服采用莫尔-库仑剪切破坏准则,管片采用板单元进行模拟。在生成顶管模型后,需将顶管模型外部板单元进行析取处理,并选择析取后的板单元生成界面单元,从而建立顶管与土体的接触,实现两者之间的相对位移。除管土设置界面之外,其余接触均为节点耦合,保证各节点变形一致。

1.3 钢顶管施工开挖面有限元模型验证

为验证泥水平衡超大直径钢顶管施工计算模型的准确性,顶管顶进15 m时,在开挖面前后选取2个监测断面,每个监测断面沿横向均匀布置11个监测点。对现场监测数据进行处理分析,数值模拟计算结果与地表沉降监测结果的对比如图2所示。图2中,x为距顶管轴线水平距离,m;S(x)为x处地表沉降量,mm;e为自然常数;DG-J01为顶管监断面1;DG-J02为顶管监测断面2。地表沉降3D颜色映射曲面如图3所示。

图2 地表沉降对比分析

图3 地表沉降3D颜色映射曲面

泥水平衡钢顶管在施工过程中扰动土体,在施工应力作用下位移场发生改变,土体产生变形并不断扩展至地表,最终导致地表沉降。由图2可知：开挖面前方监测断面沉降槽宽度小于其后方沉降槽宽度,两者连线近似呈梯形分布。而对于同一监测断面沉降槽宽度基本接近,同时地表沉降特性基本符合Peck沉降槽曲线(见图3),均呈现出以顶管轴线为中心的正态分布,从而验证了数值模拟参数取值的合理性,可为后续超大直径钢顶管施工开挖面稳定性和破坏形态计算提供计算模型。

1.4 顶管施工开挖面稳定性分析

1.4.1 破坏模式界定

超大直径钢顶管施工,其开挖面力学特性非常复杂,为对开挖面破坏模式进行界定,需考虑不同支护压力作用下地表沉降特性,如图4所示。图4中,σ为支护压力;σ0为初始静止土压力;σa为主动极限支护压力;σp为被动极限支护压力。

图4 开挖面破坏模式界定

由图4可知：当支护压力等于开挖面初始静止土压力(σ=σ0)时,开挖面周围土体受力平衡,处于相对稳定状态。随着超大直径钢顶管施工开挖面支护压力的减小,在开挖面前方,土体颗粒逐渐向左移动,上方土体发生朝向开挖面的位移,形成地层空洞。当支护压力等于主动极限支护压力(σ=σa)时,开挖面发生主动失稳破坏,地表产生沉降。当支护压力等于被动极限支护压力(σ=σp)时,支护压力向右挤压土体,发生相对错动,土体发生屈服变形,导致地表隆起。因此,可以采用开挖面支护压力是否大于地层静止土压力的方法来判定开挖面的破坏模式,并将其分为主动和被动两个破坏区。为了方便研究开挖面破坏模式,引入支护应力比λ,其表达式为：

λ=σ/σ0,

其中：σ为钢顶管施工开挖面支护压力,kPa;σ0为钢顶管持力层静止土压力,kPa。

1.4.2 顶管施工开挖面失稳破坏动态分析

超大直径钢顶管在施工过程中由于工作井顶管顶力不足,极易达到极限支护压力值,造成地表塌陷,开挖面发生失稳破坏。本文通过逐渐减小支护压力比,分析超大直径钢顶管施工开挖面不同监测点水平位移,得出开挖面破坏模式。支护压力比与超大直径钢顶管施工开挖面水平位移关系曲线如图5所示。图5中,λcr为失稳临界值;λu为失稳极限值。

由图5可知：超大直径钢顶管施工开挖面失稳发展过程分为土体稳定、局部失稳和整体失稳3个阶段。当开挖面支护压力等于初始静止土压力时,土体发生弹性变形;随着支护应力比的减小,曲线近似呈直线分布,由于土拱效应的影响,土体保持稳定。当支护压力比为0.40时,开挖面处于失稳临界状态,此时开挖面前方区域侧压力系数达到最大值,土拱逐渐发挥强度。随着支护压力比继续减小,土拱区不断向地表发展,开挖面测点水平位移逐渐增加,土体发生局部失稳破坏,地表出现微小沉降。当支护压力比为0.15时,开挖面处于失稳极限状态。若支护应力比进一步减小,则开挖面测点水平位移急速增加,发生整体失稳破坏。

图5 支护压力比与开挖面水平位移关系曲线 图6 开挖面破坏模式

由开挖面破坏模式(见图6)可知：超大直径钢顶管施工,开挖面前方土体受到扰动,初始地层应力状态被打破,在其前方出现滑动破坏区。随着该区域不断向上发展,开挖面顶部土颗粒产生松动,出现松动破坏区,此时土体竖向土压力逐渐减小,在水平土压力作用下,土颗粒间相互楔紧,形成土拱区。随着开挖面支护压力的减小,土拱区沿竖直方向逐渐向上发展,原有土拱破坏,新的土拱逐渐形成并发挥强度,当移动至地表时,土拱区发生破坏,地表出现整体失稳塌陷面,此时开挖面已完全失去承载能力,发生整体失稳破坏。

2 楔形体理论极限平衡分析

2.1 楔形体计算模型的修正

对于开挖面稳定性分析,目前多采用三维楔形体计算模型进行极限支护压力的计算,开挖面破坏机制范围由楔形体和棱柱体两部分组成。分析数值模拟结果可知：开挖面发生失稳破坏时,地层内部变形沿竖直方向贯通至地表;地表沉降范围并非是规则矩形,而是呈现出前窄后宽,具有一定角度的等腰梯形。因此,改进传统的三维楔形体计算模型,将其上方的棱柱体修正为梯形体,并考虑侧面摩擦力对开挖面极限支护压力的影响,修正前后计算模型分别如图7和图8所示,其中,α为滑块破裂角;β为梯形底角;D为钢顶管的直径;H1为上覆土层厚度;倾斜面ABJK为楔形体滑动面;AKI和BJH均为楔形体侧面。

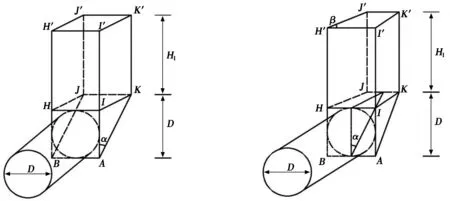
图7 楔形体计算模型(修正前) 图8 梯形楔形体计算模型(修正后)

2.2 开挖面极限支护压力计算方法

本文基于梯形楔形体模型,利用极限平衡理论对该计算模型进行受力分析,列出水平和竖直方向的极限平衡方程,推导适用于超大直径泥水平衡钢顶管施工开挖面发生失稳破坏时的极限支护压力表达式,梯形楔形体滑动块极限破坏计算模型[21]如图9所示,其中,D′为梯形楔形体上底长度;L为梯形楔形体的高;L′为梯形楔形体的腰长;D为钢顶管的直径。

S+Tsinα+2Tssinβsinα-Ncosα=0;

(1)

V+G-Tcosα-2Tssinβcosα-Nsinα=0,

(2)

联立解得：

(3)

(4)

其中：S为钢顶管施工开挖面支护力,kPa;N为楔形体滑动面支护力,kPa;T为滑动面剪力,kN;Ts为楔形体侧面剪力,kN;α为楔形体滑动面与竖直面的夹角,(°);β为梯形底角,(°);V为楔形体上覆土压力,kN;G为梯形楔形体滑块重力,kN。

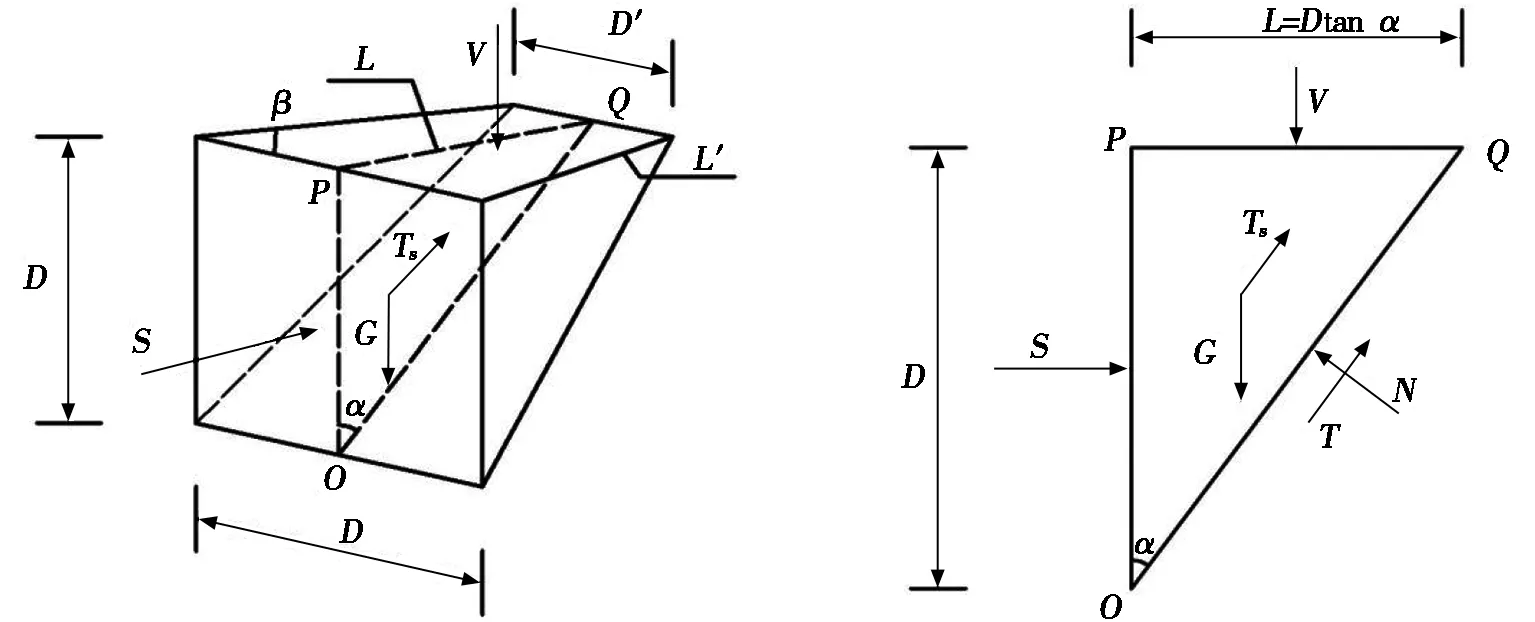
(a) 三维滑动块极限破坏受力模型 (b) 极限破坏平面受力分析图

梯形楔形体滑块重力G[21]为：

(5)

梯形楔形体上覆土压力V[21]为：

(6)

其中：σv为梯形楔形体的竖向应力,kPa。根据考虑土拱效应的Terzaghi松动土压力理论进行求解,上覆土体受力模型如图10所示。松动土体微元的竖向平衡方程为：

σvS+γSdz=(σv+dσv)S+(D+D′+2L′)τdz;

(7)

τ=c+λlσvtanφ,

(8)

联立式(7)和式(8)整理得：

(9)

其中：SHIKJ为梯形面积,m2;τ为地质界面剪应力,kPa;λl为侧压力系数,取0.4;γ为土体容重,kN/m3;φ为土体内摩擦角,(°);c为土体黏聚力,kPa。解此一阶非齐次常系数微分方程得：

(10)

当z=0时,σv=q,代入式(8)得：

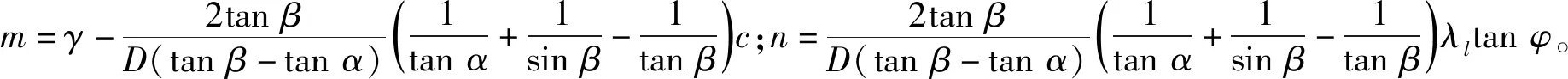
(a) 3D开挖面土压力计算模型 (b) 二维开挖面受力分析图

楔形体滑动面ABJK上的剪力T[22]为：

(11)

联立式(4)和式(11)解得：

(12)

楔形体侧面AKI和BJH上的剪力Ts[22]为：

楔形体侧面沿竖直方向的应力随埋深的增加呈线性变化,其应力分布如图11所示。竖直面AKI(BJH)上某一深度的竖向应力为：

(13)

则作用于楔形体侧面的剪力为：

dTs=[c+λσv(z)tanφ]ds。

(14)

对式(14)进行积分得总剪力为：

(15)

将式(5)、式(6)、式(10)、式(12)和式(15)代入式(3),得到超大直径钢顶管施工开挖面支护力S,钢顶管施工开挖面极限支护压力表达式为：

(16)

由式(14)可知,基于极限平衡理论推导出的开挖面极限支护压力表达式仅与楔形体破裂角α和梯形底角β有关,从而简化了繁琐的计算过程。在此理论分析基础上,本文结合上述深圳市钢顶管项目工程,将施工参数代入极限破坏计算模型,从而得到泥水平衡超大直径钢顶管施工开挖面的极限支护压力,此时对应的滑动块破裂角为极限破裂角。在此基础上,进一步将梯形底角与极限支护压力值进行曲线拟合,得到两者函数关系。

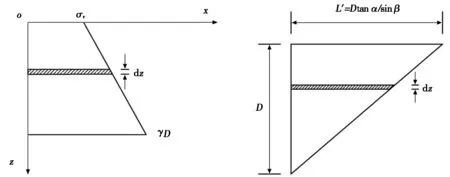
(a) 楔形体侧面竖向应力分布 (b) 楔形体侧面不同区域面积积分

3 工程实例计算分析

3.1 开挖面滑动块破裂角分析

结合上述深圳市超大直径钢顶管项目工程的土体力学参数(见表1),将不同梯形底角代入式(16),计算得到开挖面滑动块破裂角与开挖面极限支护压力的关系曲线,如图12所示。根据楔形体计算模型得到的开挖面支护压力值随滑动块倾角的增加呈现出先增大后减小的趋势。随着梯形底角不断增大,顶管施工开挖面达到失稳破坏所需的极限支护压力不断增加,对应的滑动块破裂角也有所增加,说明梯形底角的增加在一定程度上能够提高开挖面的自稳能力。当梯形底角β=80°时,开挖面达到极限失稳状态所对应的滑动块破裂角为43°,该角度与文献[23]试验研究结果基本一致。由此可知,采用楔形体计算模型确定开挖面滑动块破裂角的方法具有一定的理论价值,可以应用于超大直径钢顶管工程。

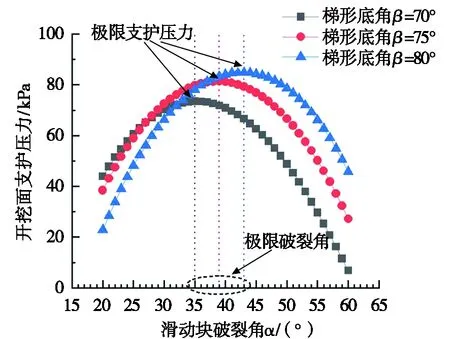
图12 滑动块破裂角与极限支护压力的关系曲线

3.2 梯形楔形体模型梯形底角分析

根据修正楔形体极限平衡理论研究结果,将开挖面发生整体失稳破坏时极限支护压力所对应的滑动块倾角代入式(16),得出梯形底角与开挖面支护压力的拟合曲线,如图13所示。计算结果显示,该理论模型最大梯形底角为79.5°,随着梯形底角的增大,开挖面极限支护压力前期呈线性快速增长趋势;当梯形底角大于75.0°时,两者近似呈指数函数关系,其表达式为：

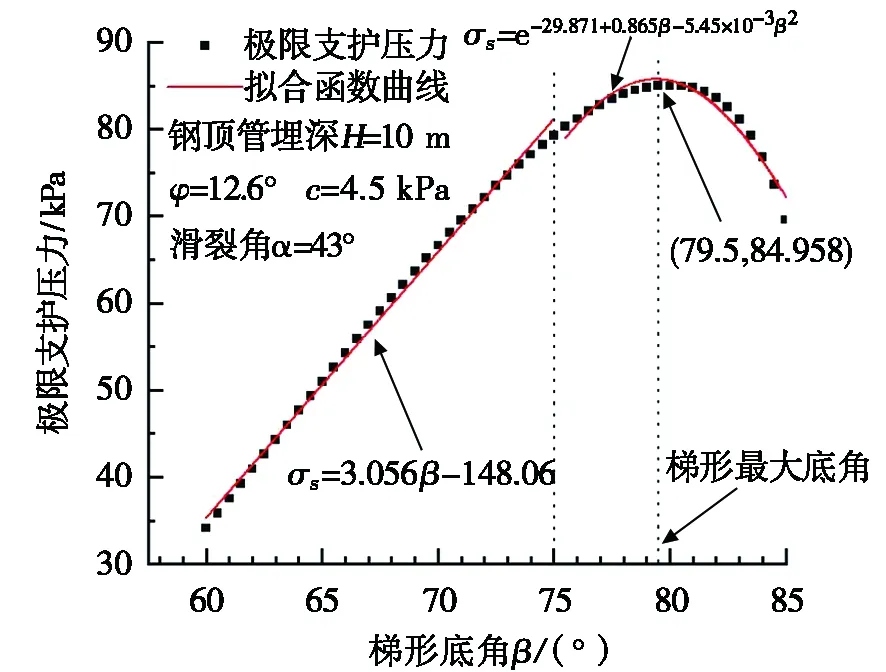
图13 极限支护压力与梯形底角的关系

(17)

3.3 楔形体理论解与数值解对比

为验证超大直径泥水平衡钢顶管施工开挖面极限支护压力计算公式的准确性,结合上述深圳市超大直径钢顶管工程项目,将相关参数代入修正楔形体模型计算公式中,对比本文计算方法得出的极限支护压力值与有限元数值模拟计算结果,如表2所示。

表2 超大直径钢顶管隧道开挖面极限支护压力对比分析

由表2可知：开挖面极限支护压力随着土体内摩擦角的增大而减小,修正后极限支护压力的计算结果普遍小于传统楔形体模型理论解,原因在于该计算模型考虑了侧摩阻力对开挖面稳定性的影响,且传统计算结果偏于保守。同时,文献[6]也揭示了传统楔形体模型存在一定局限性。修正后的理论解与数值模拟计算结果基本吻合,两者理论偏差均在可接受范围内,说明超大直径钢顶管施工开挖面的失稳模式基本符合楔形体-梯形体模型的假设,采用该理论模型得到的极限支护压力值能够较好地应用于工程实践。

4 极限支护压力影响因素分析

4.1 内摩擦角的影响

超大直径泥水平衡钢顶管在施工中,开挖面周围土体因应力松弛造成地层损失,出现由开挖面延伸至地表的地层空洞,若土体内摩擦角较小,则土颗粒间的咬合力减小,导致地表塌落。因此,需对内摩擦角与开挖面极限支护压力的关系进行定量分析以确保超大直径钢顶管的安全施工,两者关系曲线如图14所示。

图14 内摩擦角-极限支护压力关系曲线

由计算结果可知：顶管施工开挖面发生失稳破坏时,极限支护压力随着土体内摩擦角的增大而减小。当内摩擦角较小时,土体抵抗剪切变形的能力减弱,极限支护压力急剧减小。当内摩擦角大于27.5°时,土体颗粒与颗粒之间发生相对位移需要克服的滑动摩擦力较大,土体自稳能力增强,极限支护压力变化幅度趋于平缓。理论上,当土体内摩擦角无限增大时,开挖面可以在无支护压力作用下保持稳定,但是在实际工程中开挖面受力状态复杂,超挖造成的地层空洞常被忽略,因此在超大直径钢顶管施工中,维持开挖面稳定的支护压力设计值应适当大于理论值,减少地层损失,确保施工安全。

4.2 黏聚力的影响

超大直径钢顶管在施工应力作用下,开挖面土体与管周土体易发生相对错动,出现剪切屈服带,开挖面上方土体在自重应力作用下产生向下位移,导致上方土体出现地层空洞或塌落现象,开挖面产生失稳破坏。黏聚力作为维持土体稳定的重要指标,探究不同黏聚力对开挖面极限支护压力的影响,具有非常重要的实践意义,两者关系曲线如图15所示。

由图15可知：随着土体黏聚力的增加,相邻土颗粒间的吸引力增强,土体自稳能力提高,开挖面极限支护压力与土体黏聚力呈线性负相关性。对于黏聚力相同的土体,随着埋深直径比的减少,开挖面极限支护压力不断降低,且下降幅度呈增加趋势,其原因在于浅埋顶管在开挖面上方不易形成压力拱,土体稳定性下降,从而导致极限支护压力下降幅度逐渐增大。因此,在实际工程中应特别重视土体黏聚力对超大直径钢顶管施工开挖面极限支护压力的影响,为确保施工安全应尽可能避免在浅埋砂土地层中施工。

图15 黏聚力-极限支护压力关系曲线

4.3 埋深直径比的影响

超大直径泥水平衡钢顶管在施工过程中,开挖面受到施工应力的影响,土体初始应力平衡状态被打破,开挖面土体变形位移不断积累,并向上部和两侧扩展,最终发展至地表导致开挖面发生失稳破坏。对于不同顶管埋深,由于受到土拱效应的影响,开挖面发生失稳破坏时所对应的极限支护压力也有所差异,根据修正的楔形体计算模型,在其他施工参数不变的情况下,埋深直径比-极限支护压力的关系曲线如图16所示。

图16 埋深直径比-极限支护压力关系曲线

由图16可知：超大直径钢顶管施工开挖面发生失稳破坏时,随着埋深直径比的增加,极限支护压力不断增加。当钢顶管埋深比较小时,顶管在顶进过程中,土体产生弹塑性变形,形成地层空洞,开挖面周围土体为填补管节空隙造成地层损失,极限支护压力迅速增加。当埋深比大于2.2时,土体水平土压力不断增加,土体在自重应力作用下相互楔紧,形成土拱。随着埋深的增加,土颗粒间楔紧效果越好,土拱效应发挥强度,开挖面极限支护压力增大幅度逐渐趋于平缓。因此,埋深直径比对超大直径钢顶管施工开挖面极限支护压力的影响在工程中不能被忽略,尤其对于摩擦角较小的土体,更应该得到重视。

5 结论

(1)超大直径钢顶管施工开挖面失稳发展过程分为土体稳定、局部失稳和整体失稳3个阶段,并伴随着土拱的形成、发展和破坏。当支护压力比为0.4时,开挖面处于失稳临界状态;当支护压力比为0.15时,开挖面处于失稳极限状态。

(2)开挖面极限支护压力随着破裂角的增加呈现出先增加后减小的趋势。当破裂角为43°时,极限支护压力达到最大值;当梯形底角60°<β≤75°时,极限支护压力比是关于梯形底角的一次函数;当梯形底角75°<β≤85°时,两者近似呈指数函数关系。

(3)开挖面极限支护压力随着土体内摩擦角和黏聚力的增加而逐渐减小。当内摩擦角大于27.5°时,土体趋于稳定。随着埋深直径比的增加,开挖面支护压力逐渐增加,当埋深比大于2.2时,变化趋势趋于平缓。