离散高阶多自主体系统的编队-合围跟踪控制

齐晓龙

(陇东学院电气工程学院, 甘肃 庆阳 745000)

多自主体系统的协调控制主要针对一致性问题、编队控制和群集控制等方面．作为多自主体系统协调控制研究的基础,一致性控制要求自主体的状态趋于一个定值或函数[1-2]．当系统中存在多个编队领导者时, 系统的一致性问题则成为合围控制问题[3-4]．编队-合围控制,即在由多个编队领导者和跟随者组成的多自主体系统中,编队领导者形成所要求的编队, 同时跟随者趋于编队领导者形成的凸包．Zheng[5], Han[6]等针对二阶多自主体系统研究了存在时延下系统的编队-合围控制问题; Gong等[7]针对高阶多自主体系统设计了基于观测器的编队-合围控制协议; Zhang[8],Zhou[9]等探讨了采样数据、时延及网络切换等因素对系统实现编队-合围控制目标的影响．时间触发机制及随机采样机制也常被用于多自主体系统的编队-合围控制研究[10-11]．在上述编队-合围控制研究成果中, 编队领导者的轨迹最终趋于编队参考函数,其值由系统的初始状态决定．本文将多自主体系统扩展为由一个虚拟领导者、多个编队领导者和跟随者组成,在已知虚拟领导者的输入信号情形下利用自主体邻接信息,考虑时变时延,分别针对编队领导者和跟随者设计编队和合围跟踪控制协议,再利用图论及Lyapunov稳定性定理给出协议有效的充分条件,以期使得编队领导者和跟随者在所设计的控制协议作用下实现编队-合围控制目标,同时跟踪虚拟领导者的任意轨迹．

1 图论与系统描述

1.1 图论

1.2 问题描述

考虑由1个虚拟领导者和N个自主体(包括M个跟随者和N-M个编队领导者)构成的多自主体网络．描述虚拟领导者的动态模型为

x0(k+1)=Ax0(k)+Bu0(k),

(1)

其中虚拟领导者的状态x0(k)∈Rn, 虚拟领导者已知的输入信号u0(k)∈Rr,A,B分别为系统矩阵和输入矩阵．描述N个自主体的模型为

xi(k+1)=Axi(k)+Bui(k),i=1,2,…,N,

(2)

其中xi(k)∈Rn,ui(k)∈Rr分别为第i个自主体的状态和控制输入．

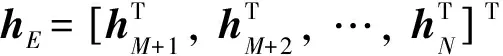
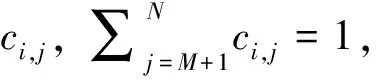
(3)

则称系统(2)实现了编队-合围控制, 并且能跟踪虚拟领导者的轨迹．

根据编队领导者和跟随者邻接集的特点, 可将Laplacian矩阵分解为

其中L1∈RM×M表示M个跟随者之间的邻接信息,L2∈RM×(N-M)为跟随者和编队领导者之间的邻接信息,L3∈R(N-M)×(N-M)为N-M个编队领导者之间的邻接信息．

假设1矩阵B是非奇异的．

假设2在多自主体网络中, 对于每个跟随者, 至少有一个编队领导者与其之间存在有向路径．

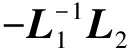
考虑时变时延, 设计如下编队-合围跟踪控制协议:

(4)

ui(k)=u0(k)+K3∑j∈Ni(xi(k-dk)-xj(k-dk)),i∈F,

(5)

式中当第i个编队领导者能接收到虚拟领导者的信息时,δi=1,否则δi=0;K1,K2,K3为常数矩阵;In为n维单位矩阵; 时变时延dk满足

d1≤dk≤d2,

(6)

其中d1,d2为已知常数．

(7)

(8)

其中Δ=diag{δM+1,…,δN},⊗表示Kronecker积,1M为M维元素全为1的向量．

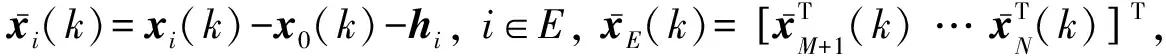
(9)

引理2若

(10)

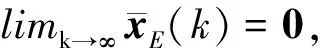
φF(k)=(L1⊗In)xF(k)+(L2⊗In)xE(k)．

(11)

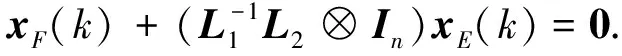
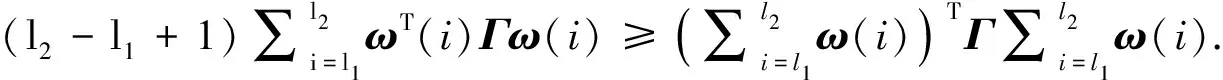
引理4[14]对于误差系统(9), 若存在正定矩阵P,Q1,Q2,Q3,R,S及矩阵L1,L2,M1,M2,N1,N2满足

(12)

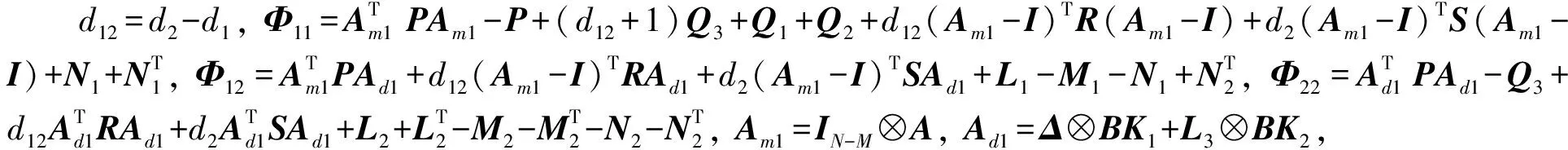
定理1若存在正定对称矩阵PE,QiE(i=1,2,3),RiE(i=1,2),RiF(i=1,2),PF,QiF(i=1,2,3), 满足式(13)～(16):

(13)

(14)

(15)

(16)

式中Ξ11=-R1E-PE+Q1E+Q2E+(d12+1)Q3E,Am2=IM⊗A,Ad2=L1⊗BK3,d12=d2-d1, 则高阶离散多自主体系统(1)(2)在协议(4)(5)的作用下能实现编队-合围跟踪控制．

V(k)=V1(k)+V2(k),

(17)

其中

(18)

(19)

则

(20)

(21)

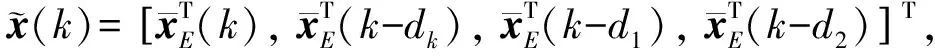
(22)

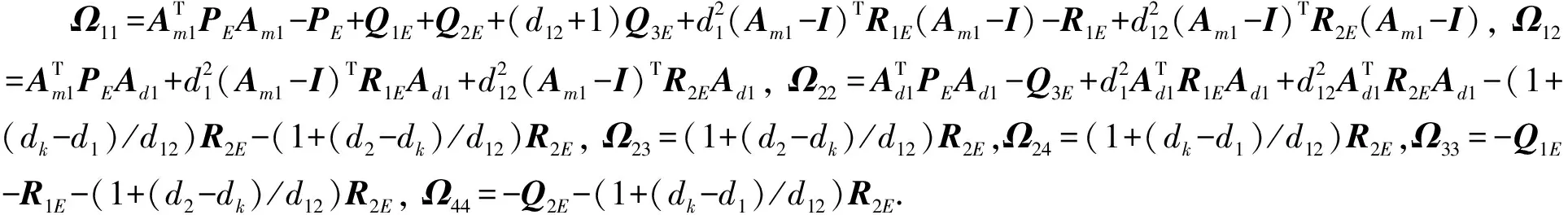
φF(k+1)=(IM⊗A)φF(k)+(L1⊗BK3)φF(k-dk)．

(23)

类似于系统(9), 当线性矩阵不等式(15)(16)成立时, 误差系统(23)渐近稳定．根据引理2, 当式(13)(16)成立时, 多自主体系统(1)(2)在控制协议(4)(5)的作用下可实现编队-合围跟踪控制．证毕．

注1通过状态转换, 将系统的编队-合围跟踪控制问题变换为分析误差系统(9)和系统(23)的稳定性问题．

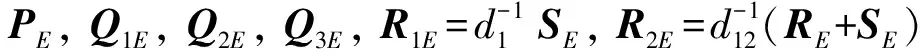
证明 当式(12)成立时, 令UE=RE+SE, 因d12=d2-d1, 故由Schur补引理, 有

(24)

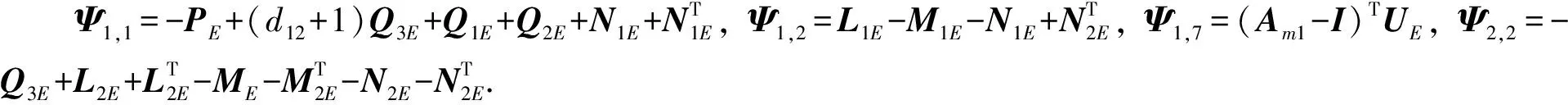
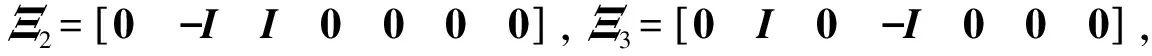
(25)

(26)

3 仿真分析

考虑由1个虚拟领导者(自主体0), 3个编队领导者(自主体3～5)和2个跟随者(自主体1～2)组成的多自主体网络,其网络拓扑如图1所示．在多自主体网络拓扑图1中,只有编队领导者才能获得虚拟领导者的信息, 并且对于每个跟随者,都至少存在一个编队领导者与其之间存在一条有向路径且满足假设2．

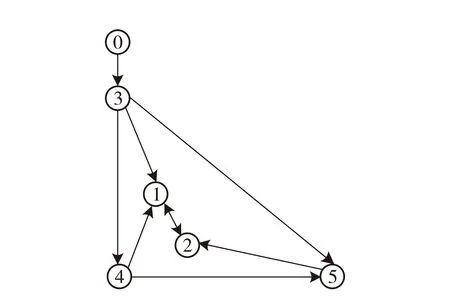
图1 多自主体网络拓扑示意图Fig.1 Network topology of multi-agent system

当K1=diag{-0.01, -0.01},K2=diag{-0.02, -0.02}时, 式(13)(14)成立, 此时,

当K1=diag{-0.01, -0.01},K3=diag{-0.01, -0.01}时, 式(15)(16)成立, 此时,

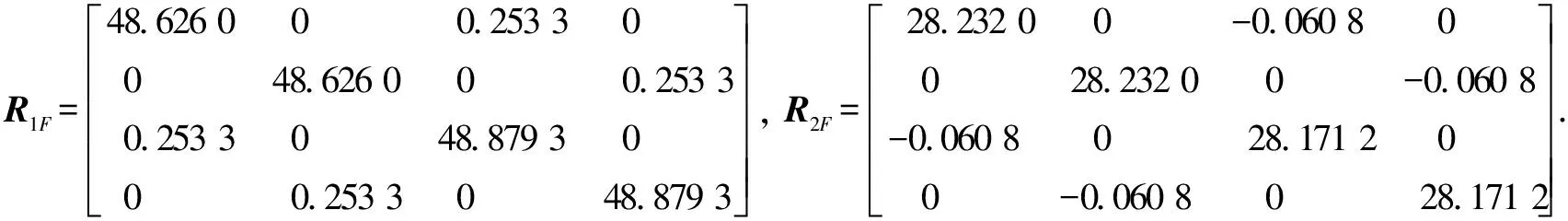
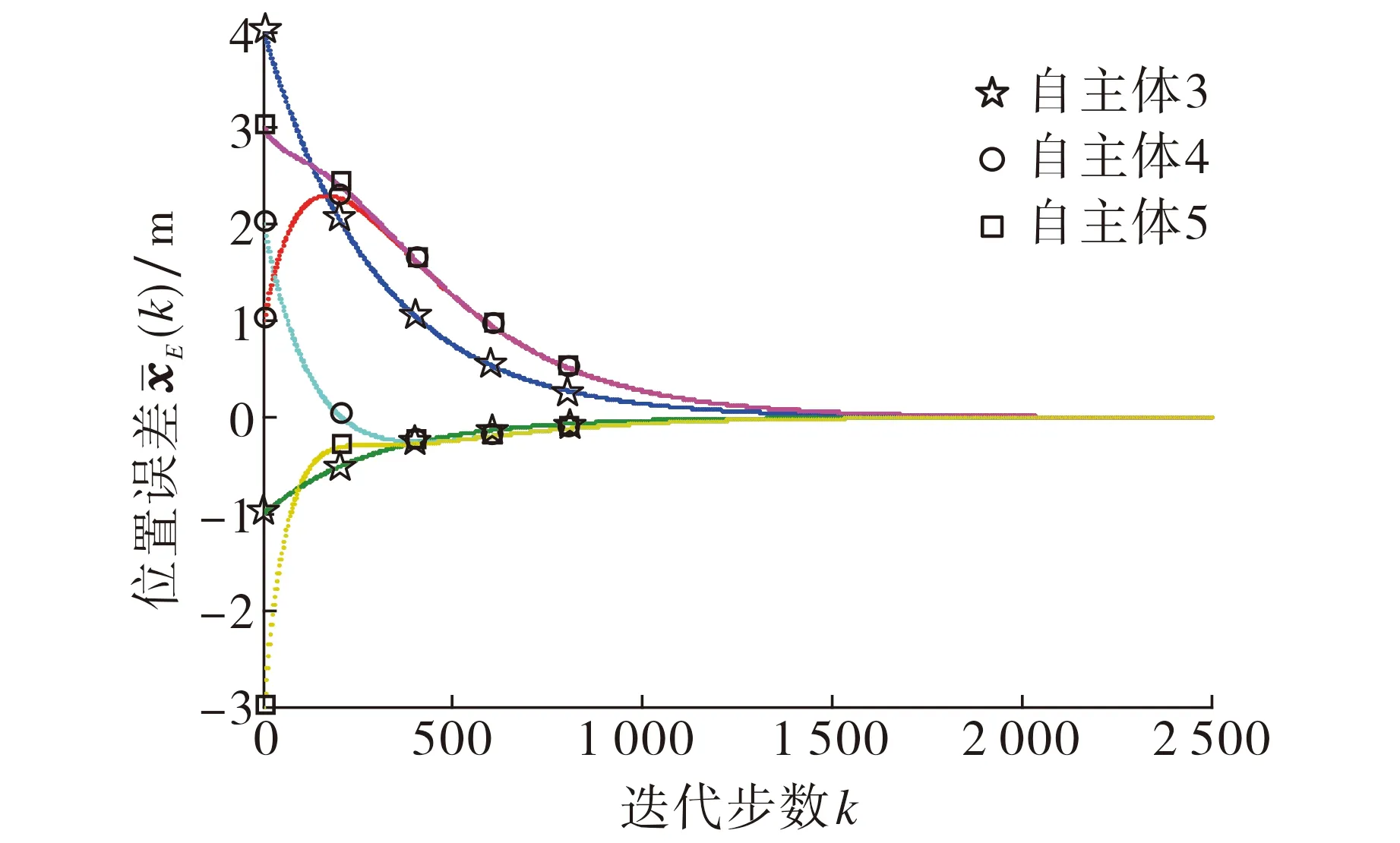
图2 误差系统(9)的状态轨迹Fig.2 State trajectories of error system (9)

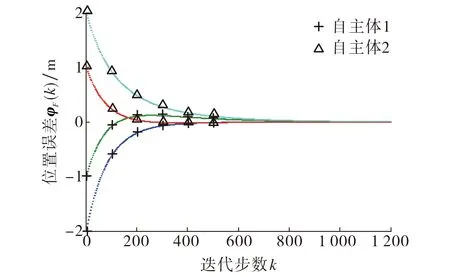
图3 误差系统(23)的状态轨迹Fig.3 State trajectories of error system (23)

为了进一步验证协议的有效性, 取初始状态x0(1)=[0,-1]T,x1(1)=[2,-1]T,x2(1)=[3,-1]T,x3(1)=[2,-1]T,x4(1)=[4,-1]T,x5(1)=[-2,-1]T,u0(k)=[1,1]T, 多自主体系统(2)在协议(4)(5)作用下的编队-合围控制仿真结果如图4所示．由图4可见: 3个编队领导者最终形成并保持预期的三角形, 并且2个跟随者趋于编队领导者形成的凸包中．

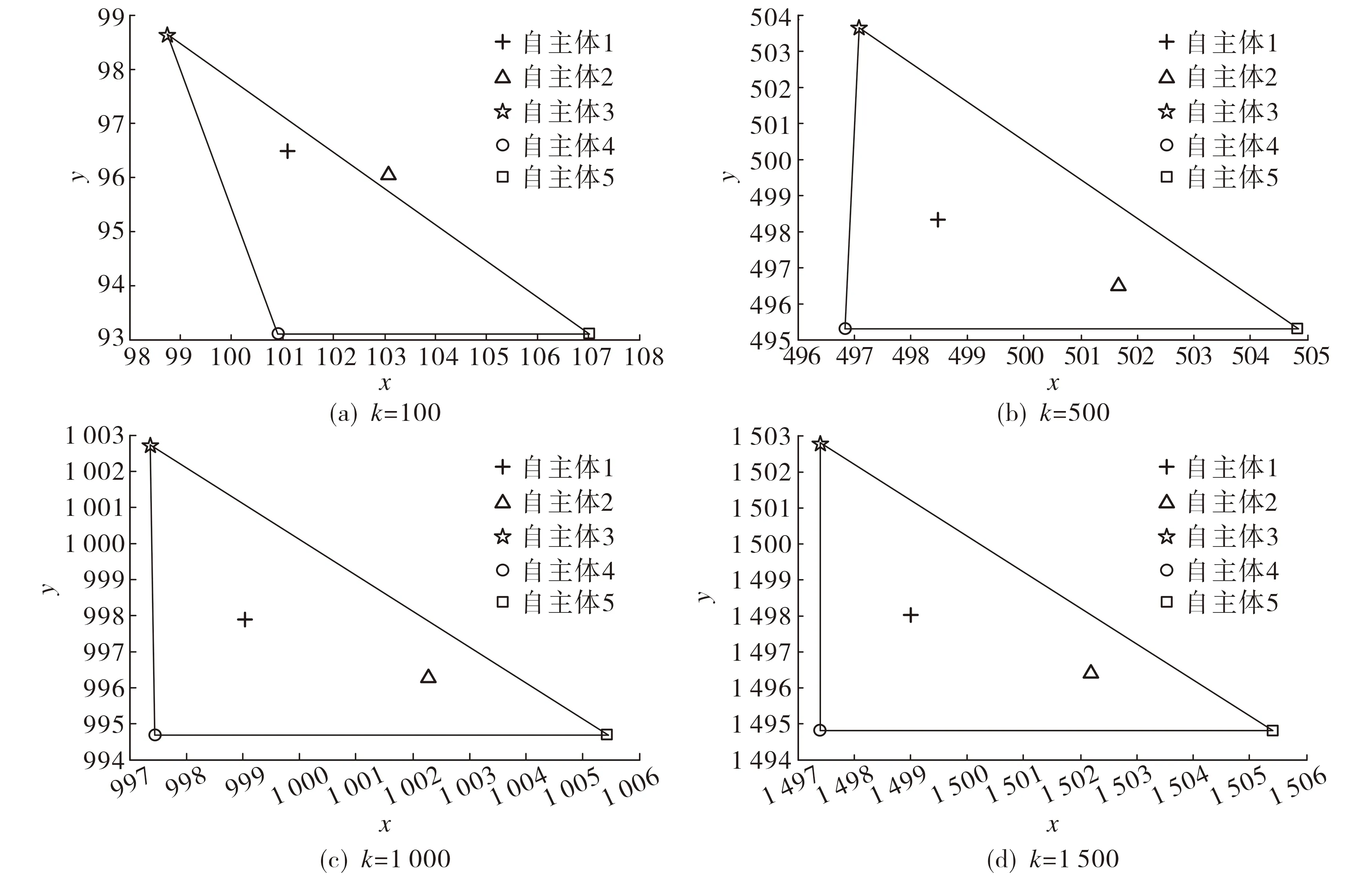
图4 系统编队合围状态仿真结果Fig.4 Simulation results of system formation encircle state

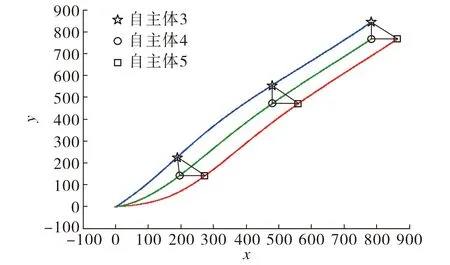
图5 系统编队合围跟踪轨迹Fig.5 Formation-containment tracking trajectories

分别取h3=[0,0]T,h4=[0,-80]T,h5=[80, -80]T, 自主体的初始状态及虚拟领导者的控制输入与图4中仿真数据相同,编队领导者自主体的跟踪轨迹如图5所示．由图5可见: 3个编队领导者自主体可形成所要求的三角形编队, 同时跟踪虚拟领导者的轨迹, 其轨迹与编队领导者 3的轨迹重合, 表明所设计的协议有效．