横向关联经验 纵深探寻本质——《相遇问题》教学实践（一）

文|王扣兰

【教学内容】

苏教版四年级下册第68、69 页。

【教学过程】

一、创设情境，激活学习迁移力

1.演一演，感知“相遇”

课前小游戏，模拟例题相遇情境。情境分两个层次，层次一：两人在两端站好，思考相遇的位置大概在什么地方，原因是什么，然后口令员喊“一、二、三、四”，行动员相向而行，最后相遇；层次二：口令员喊“一、二、三、四”，行动员每走一步，喊出自己行走的距离，最后相遇。教师记录学生的活动过程，拍成小视频。

2.想一想，体悟“特征”

师：课前我们玩了一个小游戏，老师将你们的活动过程拍成了小视频，想不想看看？边看边思考你们是怎么玩这个游戏的。

生：我和小明站在直线的两端，同时出发，面对面走，直至相遇。

生：我和小芳每人走四步，然后相遇了，我每步是70 厘米，小芳每步是60 厘米。

师：老师捕捉到这样几个关键词：两端、同时、面对面（相向）、相遇，这就是我们今天要学的相遇问题的特征。

3.说一说，唤醒“经验”

师：在学习新内容之前，先来看这样一道题。

出示题目：

小明从家出发去学校，每分钟走70 米，走了4 分钟，小明家到学校距离多少米？

生：70×4=280（米），速度×时间=路程。

师：这道行程问题只涉及到小明一个人，我们称之为“单人行程问题”。今天我们要学的相遇问题，你觉得是什么问题呢？

生：两人行程问题。

二、三学联动，增强学习自主力

1.自主探学，展开研究

出示例题：

师：一起来看这样一道生活中的相遇问题。读完题目，你有什么想说的？

生：与我们课前玩的小游戏是一样的。

师：你能联系课前的运动过程，将这个相遇问题画下来吗？

活动要求：

想一想：题中包含的问题和条件是什么？

画一画：将你活动的过程画下来，让人一眼就看出其中包含的条件和问题。

说一说：四人小组交流，你是如何整理出条件和问题的。

（学生自主探究，教师巡视）

2.互动辩学，交流互鉴

师：老师这里收集了两位同学的作品（出示作品①和作品②），你能读懂这两幅作品吗？如果读懂了，你更喜欢哪一个作品，为什么？

作品①

作品②

生：我更喜欢②号作品，她将条件清楚地罗列出来，还提出了问题。①号作品没有提出问题。

生：①号作品排列得很整齐，但②号作品是用表格整理的，看上去更清晰。

师：这两位同学都是用列表的方法来整理条件和问题的，让人一眼就看清了小明和小芳的信息。让我们再来看看别的方法（出示作品③和作品④）。有请这两位同学上台说一说你是怎么画的。

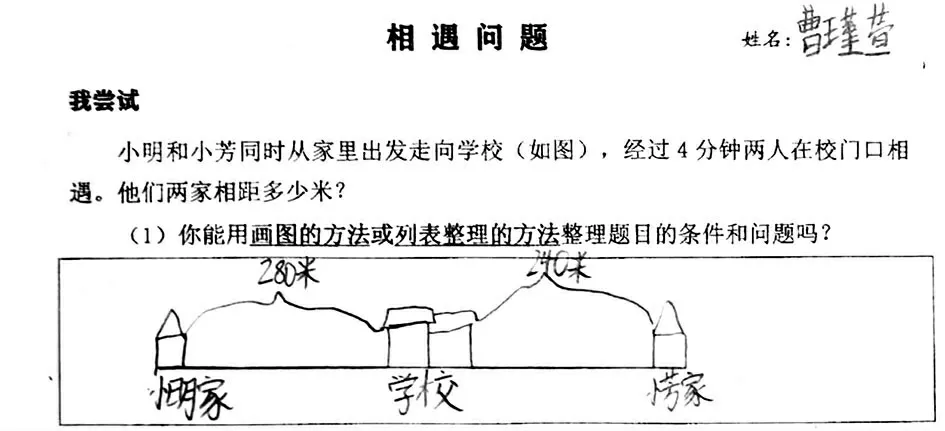
作品③

生：小明每分钟走70 米，他走了4 分钟，共走了280 米。小芳每分钟走60 米，她也走了4 分钟，共走了240 米。所以我在图上标出了小明和小芳走的路程。

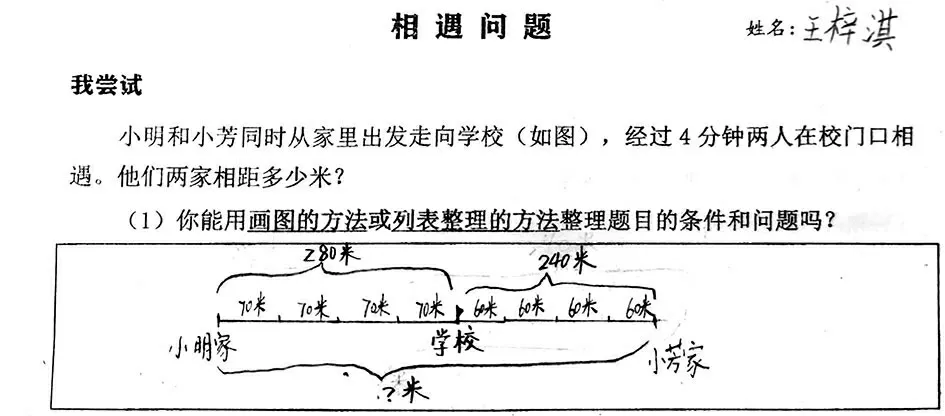
作品④

生：小明和小芳都走了4 分钟，所以我用了4 小格来表示，他们每分钟走1 小格，小明每格都是70 米，小芳每格都是60米，我还算出了他们分别走的路程，标出了问题。大家还有要补充的吗？

生：我觉得④号作品更详细，他按照要求画出了所有的条件和问题。③号作品算出了各自行走的路程，但各自的速度和时间没有表示出来。

生：我同意他的观点，我还想说，其实④号作品只需要表示出条件和问题就可以了，不需要计算，所以280 米和240 米是不需要标记出来的。

生：我还想补充，因为小明和小芳都走了4 分钟，小明的速度快，所以小明行走的路程要比小芳行走的路程长一些，那么学校的位置就不能画在正中间。

生：我认为还要标上方向，用箭头表示一下他们是朝着什么方向走的。

师：现在这幅线段图，你们觉得如何？

（学生补充，教师添补）

师：刚才同学们说的句句在理，大家听的也是频频点头。你一言我一语，线段图的画法就出来了。现在你们知道一幅完整的线段图包含了什么？

生：条件、问题和方向……

3.对比评学，完善思维

师：根据这幅完整的线段图，你知道小明家到小芳家的路程该怎么求吗？

（学生先独立思考并写出自己的思考过程，之后同桌交流再进行汇报）

生：先算小明家到学校的路程，然后算小芳家到学校的路程，最后相加就是总路程。

师：表述完整，思维清晰，点赞！你刚才说的就是这道题的数量关系。现在你们能根据这个数量关系列式解答了吗？

（学生独立列式70×4+60×4，说清楚分别算的是什么）

师：还有不同的算法吗？

生：（70+60）×4。

师：谁懂他的意思？

生：“70+60”是小明和小芳1分钟走的总路程，再“×4”，就是4分钟走的总路程了。

师：能看懂别人的想法，你是一个爱动脑筋的好孩子！70是小明的速度，60 是小芳的速度，70+60 就是他们俩的速度和，速度和的意思就是小明和小芳1 分钟走的总路程。看着线段图想一想，从图中你找到了几个速度和？

［学生配合动画，边指边说。明确总路程包含了4 个速度和，所以是（70+60）×4］

师：对比这两种方法，你有什么发现？

生：我发现结果都是520，答案是一样的。

生：我发现70×4+60×4=（70+60）×4，运用了乘法分配律，所以答案是一样的。

师：看来运用乘法分配律，我们可以从一种方法想到另一种方法，还能互相检验，真不错。

生：我发现这两种方法都是运用的“速度×时间=路程”这个数量关系。70×4 是小明的速度×时间，60×4 是小芳的速度×时间，加起来是总路程；而（70+60）×4，是速度和×时间，速度和也是速度。所以我认为这两种方法本质上是一样的。

师：你已经进入了深度学习状态，学习就是要抓住本质。回顾我们解决问题的过程，你有什么想说的？

生：画线段图的方法能准确地反映出数量间的关系，易于发现并解答所求问题。

生：列表的方法清晰明了地表达了信息及其相互的联系，便于分析、比较。

三、思维提升，促进学习思考力

1.相背行程问题

师：小明和小芳现在放学回家了，其他条件都不变，你能用手指演示他们放学回家的过程吗？

（学生动手演示）

师：上学与放学，有什么异同点呢？

生：上学是面对面走，放学是背对背走。箭头画法不一样，其他都是一样的。

师：是相遇问题吗？

生：是相遇问题。只是原来的相遇点变成了现在的出发点而已，其他特征都是一样的。

师：那从学校出发，各自回家，两家相距多少米？会求吗？

……

2.环形反向行程问题

出示题目：

小芳和小明在环形跑道上跑步，两人从同一地点出发，反向而行。小芳的速度是4 米/秒，小明的速度是6 米/秒，经过40 秒两人相遇。环形跑道长多少米？

师：这次是相遇问题吗？与之前的又有什么不同呢？

生：这次是环形，不是直线了。

师：其实我们还可以借助手指，模拟跑一跑。

（学生动手模拟演示）

师：你有什么感觉？

生：与放学特别像，也是背对背反向而行，只不过放学走的是直线，这个跑的是环形。

师：如果老师借你“一把剪刀”，请你将跑道剪开来，再拉直，你会从哪里剪开？

生：从出发点剪开，拉直就与例题一模一样了，从两端开始跑。

师：你们是一群会研究的孩子！其实将环形剪开拉直，这其中渗透了一种“化曲为直”的思想，巧妙地转化为我们学过的知识。

3.迁移行程问题

师：相遇问题还会出现在什么地方呢？让我们一起来看一看。

出示题目：

两个工程队合开一条隧道，分别从隧道的一端同时向中间开凿。第一队每天开凿12 米，第二队每天开凿15 米，经过8 天正好凿通。这条隧道长多少米？

师：借助你的小手，模拟“从隧道的一端同时向中间开凿”，每凿一步，配上长度。凿几步？

生：凿8 步。（边凿边说）

师：相遇了吗？你从哪里知道相遇了？

生：凿通了，就是两队相遇了。

师：第一队每天开凿12 米，这是第一队的工作效率，其实咱们可以把12 看作是第一队的开凿速度，这样就又变成了一道行程问题。你会做了吗？

四、文化培根，渗透民族凝聚力

1.视频赏析，了解詹天佑

学生观看视频《詹天佑》，了解詹天佑是“中国近代工程之父”。1905~1909年，他主持修建了中国自主设计并建造的第一条铁路——京张铁路，创设的“两端凿进法”和“中部凿井法”震惊中外。

两端凿进法

中部凿井法

2.方法研究，激发爱国心

师：观看了这个视频，你有什么想说的？

生：两端凿进法就是我们今天学习的相遇问题。

生：中部凿井法，从中间挖到底，然后里面也有两支队伍。①队与②队两端对凿，③队与④队两端对凿，大大提高了工作效率，詹天佑真伟大。

生：原来学好数学，还能在工程上有这么大的助益，我要学好数学，长大做一个对祖国有用的人！

……