基于速度分裂法的翼型阵风响应及减缓数值模拟

高 坤，郭同庆，纪哲翰，周 迪，陆志良

(南京航空航天大学 非定常空气动力学与流动控制工业和信息化部重点实验室，南京 210016)

0 引 言

阵风载荷响应作为一种气动弹性动力响应问题，是指飞行器在大气中飞行时遇到突然的阵风扰动，这一扰动气流将改变飞机气动升力面的有效迎角，引起升力等的突然改变，使得飞行器产生涉及弹性变形的阵风载荷响应。当飞行器处于阵风环境中时，飞行器结构将承载较大的阵风载荷，这将导致飞行器操纵困难且容易发生结构疲劳损坏。随着航空科学技术的发展，大型飞行器的结构设计朝着低重量和大柔性方向发展，这导致阵风对大型飞行器的飞行影响更为复杂[1]。因此，对于现代飞行器设计，其阵风响应分析的非定常气动模型由传统线化理论逐渐转向更为准确的CFD技术，其中阵风效应的嵌入主要分为远场边界条件法和给定流场阵风速度法两类。

将阵风加入CFD程序最直接的方法是修改计算域远场边界条件，称为远场边界条件（far-field boundary condition, FBC）法[2]。该方法为防止因计算域网格分辨率不足引起数值耗散导致阵风响应计算精度下降，要求计算域网格从物体表面到远场边界均需要非常精细，这将导致高昂的计算成本。为此，Tang和Bader[3]提出根据阵风在计算域中所处位置的变化对计算网格进行局部细化，该方法采用高阶多项式插值来重新分布网格点以获得阵风区域更新后的精细网格[4]。

给定速度法根据每一时刻阵风场在计算域中的空间位置来计算阵风速度，因此不存在远场边界条件法中因远离物面区域网格分辨率不足而引起的数值耗散问题，被广泛应用于阵风响应数值计算。给定速度法包括网格速度法（field velocity method, FVM）和速度分裂法（split velocity method, SVM）。其中，FVM由Parameswaran和Bader提出[5]，该方法借用动网格系统流动控制Euler/N-S方程，将阵风速度等效为流场当地网格速度来模拟阵风运动，但实际并不会引起网格运动。他们采用FVM模拟翼型穿越阶跃阵风时的气动响应，计算结果与理论分析结果十分接近。然而，FVM并非通过严格理论推导得来[6]，也没有考虑翼型对阵风的影响。顾宁等[7]指出当FVM应用于N-S方程时需要加入黏性通量修正。相比而言，由Wales等[8]提出的SVM则是以非定常Euler/N-S方程为基础，将阵风条件下的流场速度分解为阵风速度与无阵风作用下的流场背景速度两部分，严格理论推导出SVM阵风模拟控制方程。与FVM相比，除阵风速度外，SVM还包括了阵风对黏性通量的影响以及与阵风时空导数相关的源项。此方法已被证明在较短阵风尺度、跨声速等条件下的阵风响应模拟中能够获得更为准确的计算结果[8]。

目前，国内还尚未开展基于SVM的飞行器阵风响应模拟和减缓研究。本文针对One-Minus-Cosine离散阵风，首先基于动态网格系统非定常N-S方程，理论推导SVM阵风响应模拟的控制方程。然后耦合翼型结构运动方程，发展基于SVM的弹性翼型阵风响应CFD/CSD时域耦合算法。进而采用控制翼型旋转，发展弹性翼型阵风载荷减缓的数值模拟方法。最后采用上述方法，开展刚性及弹性翼型阵风响应和减缓分析。

1 阵风模型

本文针对One-Minus-Cosine型离散阵风开展翼型阵风响应分析。飞行器以速度V水平飞行，突然受到速度为wg的垂向阵风作用。wg为阵风速度Vg在直角坐标系下的垂向分量，定义如下[9]：

其中：Lg为阵风尺度；wg=Vtan(Δα)为阵风速度幅值；Δα为阵风速度幅值等效迎角。

2 阵风响应CFD模拟方法

2.1 网格速度法（FVM）

本节简要给出FVM[10-11]的控制方程，便于与SVM方法进行比较。动态网格系统下非定常N-S方程为：

其中：˜ 、为背景流场速度的速度分量；xt、zt为网格速度Vt的分量；ρ为流体密度；E为单位质量流体总能；p为流体压强；γ为比热比。

根据相对运动原理，如果计算域网格的运动速度为Vt，则等价于在计算域静止情况下受到速度为-Vt的气流作用[12]。因此，基于动态网格系统非定常N-S方程（2），FVM将阵风速度表示为相反方向的网格速度来模拟阵风作用[13]，即：

需要注意的是，FVM只是利用了网格速度的概念，在实施过程中并不引起实际的网格运动。尽管FVM是目前阵风响应CFD分析的主要方法，但该方法并未得到严格的理论阐明。

2.2 速度分裂法（SVM）

SVM将阵风条件下的流场速度分解为阵风速度与流场背景速度两部分，即

其中，u、w为流场总速度V的速度分量。为了开展考虑气动弹性的阵风响应分析，接下来将现有的基于固定网格系统的SVM方法[14]拓展至动态网格系统。包含阵风作用的动态网格系统下非定常N-S方程可写为：

联合式（5）～式（7），并利用背景流场的连续方程和动量方程，可得SVM的控制方程为：

其中黏性应力张量的表达式为：

其中，µ为黏性系数。式（8）中附加源项为：

若采用Euler方程，黏性通量为0，则附加源项为：

Sm、Se分别定义如下：

不难看出，相比于SVM，传统FVM的动量方程和能量方程缺少了上述附加源项。该源项与阵风场的时间和空间导数相关，反映了背景流场对阵风场的影响。对于小尺度阵风或存在激波情形，附加源项的作用将会凸显。

本文离散阵风形式由式（1）给定，因此源项中阵风相关的导数可以解析求解。采用有限体积法、双时间推进法[15]求解包含阵风作用的动态网格系统下的非定常N-S方程（8），采用并行算法提高计算效率；基于RANS模拟湍流，湍流模型选用SA一方程模型[16]。远场采用无反射边界条件，物面采用黏性无滑移边界条件，即本文后续弹性翼型阵风响应及载荷减缓计算均采用无限插值法（TFI）[17]生成动态网格。

3 弹性翼型阵风响应CFD/CSD时域模拟方法

3.1 三自由度结构运动方程

图1给出了一个具有沉浮、俯仰和控制面偏转的三自由度典型二元翼段力学模型。图中三个自由度为：刚心E的沉浮位移h，向下为正；翼段绕刚心的俯仰角位移α，抬头为正；控制面偏转角 β ，向下偏转为正。弹性轴E距离翼弦中点的距离为ahb，ah为基于半弦长b的无量纲距离，弹性轴在翼弦中点之后时ah＞0。Cβb表示控制面铰链轴距翼型弦线中点的距离，其气动弹性运动方程为[18-21]：

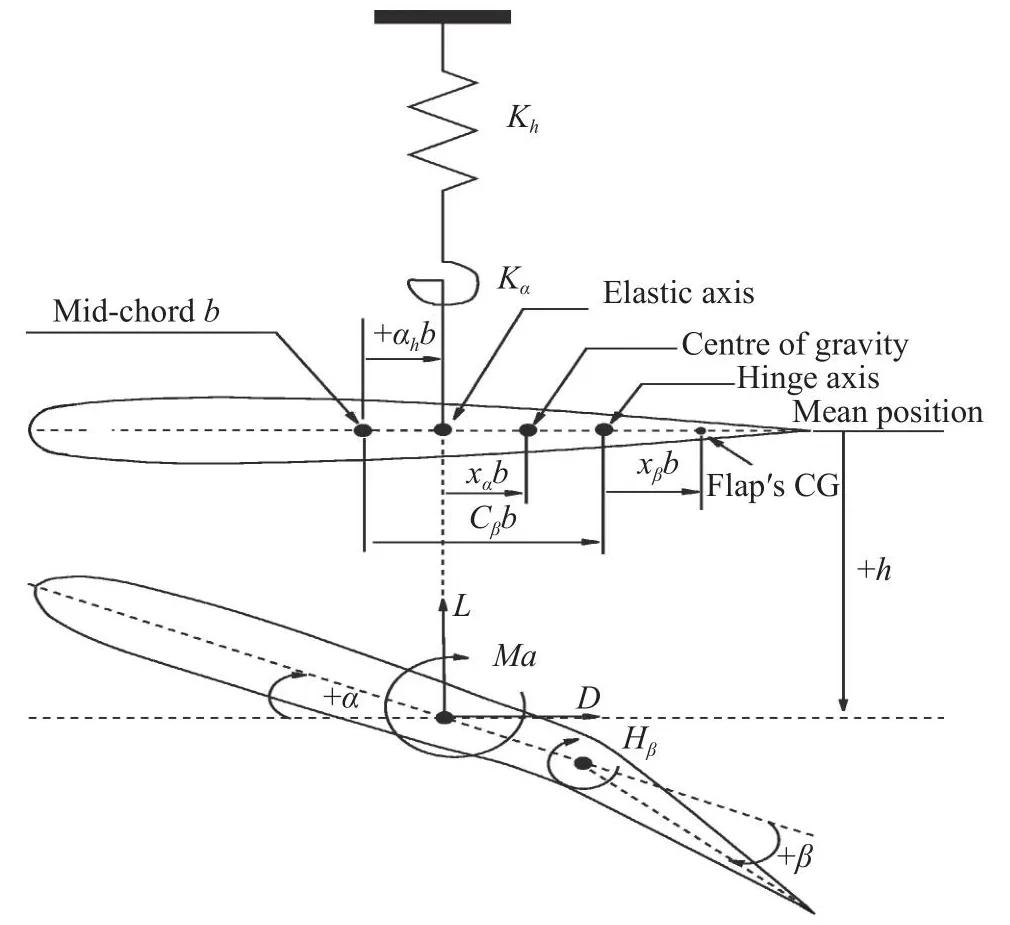
图1 三自由度典型翼段力学模型[21]Fig.1 Sketch of an airfoil with three degrees of freedom[21]

其中：m为翼段质量；Iα、Iβ分别为翼段绕刚心和控制面绕铰链轴的转动惯量；Sα、Sβ分别为翼段和控制面的质量静矩；Th、Tα和Tβ分别为翼段的沉浮、俯仰和控制面转动阻尼系数；Kh、Kα和Kβ分别为翼段的沉浮、俯仰和控制面转动刚度；L、Mα和Hβ分别为升力、俯仰力矩和铰链力矩；CL、Cm和CH分别为升力系数、俯仰力矩系数和铰链力矩系数； ρ∞为自由来流密度；c为翼型弦长。

式（16）的无量纲形式为：

为了便于在时域中求解结构运动方程（18），将其转换为状态空间形式：

其中，I为单位矩阵。

本文采用隐式欧拉法求解方程（20）：

得到n+ 1时刻的状态变量：

3.2 CFD/CSD时域耦合计算流程

给定计算状态，首先不考虑阵风作用，CFD计算获得该状态下的定常流场，然后基于定常流场开展阵风响应时域计算。基于定常流场，引入阵风场，在时域内耦合求解气动方程和结构运动方程，从而求解出阵风作用下翼型气动响应和结构位移响应。

4 基于翼型俯仰运动的阵风减缓

类似旋转翼尖，本文尝试通过控制翼型俯仰运动来进行阵风减缓。将翼型的俯仰控制角度αc与其位移响应、速度响应和加速度响应联系起来，

其中，G1、G2、G3、G4、G5、G6为控制系统增益。

则 式 （18） 右 侧 的 σa应 改 写 为 σ =σa+σc， 其 中为控制力向量。

5 算例分析

5.1 刚性翼型阵风响应计算

分别采用FVM和SVM方法，开展NACA0012刚性翼型的One-Minus-Cosine阵风响应计算分析。计算条件为：Ma= 0.3，迎角 0°，Re= 7.0 × 106；力矩参考点位于0.4c；定义无量纲时间S=2V∞t/c。采用C型结构网格，阵风从远场边界外进入计算域。根据文献[8]中不同网格数对比计算结果，翼型周向和法向网格数取为257 × 129。翼型弦长c= 7.5m，远场边界位于15倍弦长处，第一层网格高度为1×10-3c，如图2所示。本节除黏性对阵风响应影响分析采用N-S方程计算之外，其余算例均采用Euler方程。

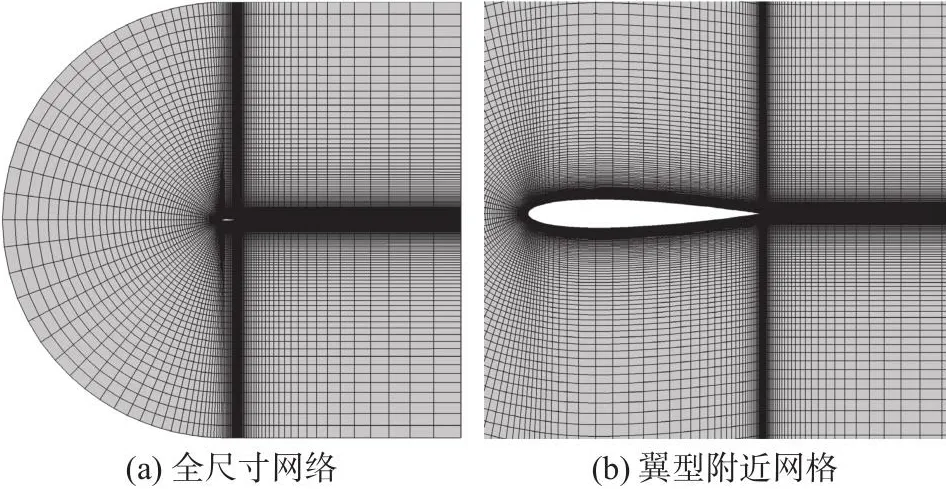
图2 NACA0012翼型计算网格Fig.2 Computational mesh for NACA0012

5.1.1 时间步长的确定

阵风尺度Lg= 1c，等效迎角 Δα= 2.0°。分别取时间步长 ΔS为 0.1、0.01和 0.001，计算结果如图3所示。对于FVM和SVM， ΔS= 0.1时的升力系数最大值和力矩系数最大值均大于 ΔS= 0.01或 ΔS= 0.001时的最大值，而 ΔS= 0.01与 ΔS= 0.001的结果相吻合，因此本文时间步长取 ΔS= 0.01。

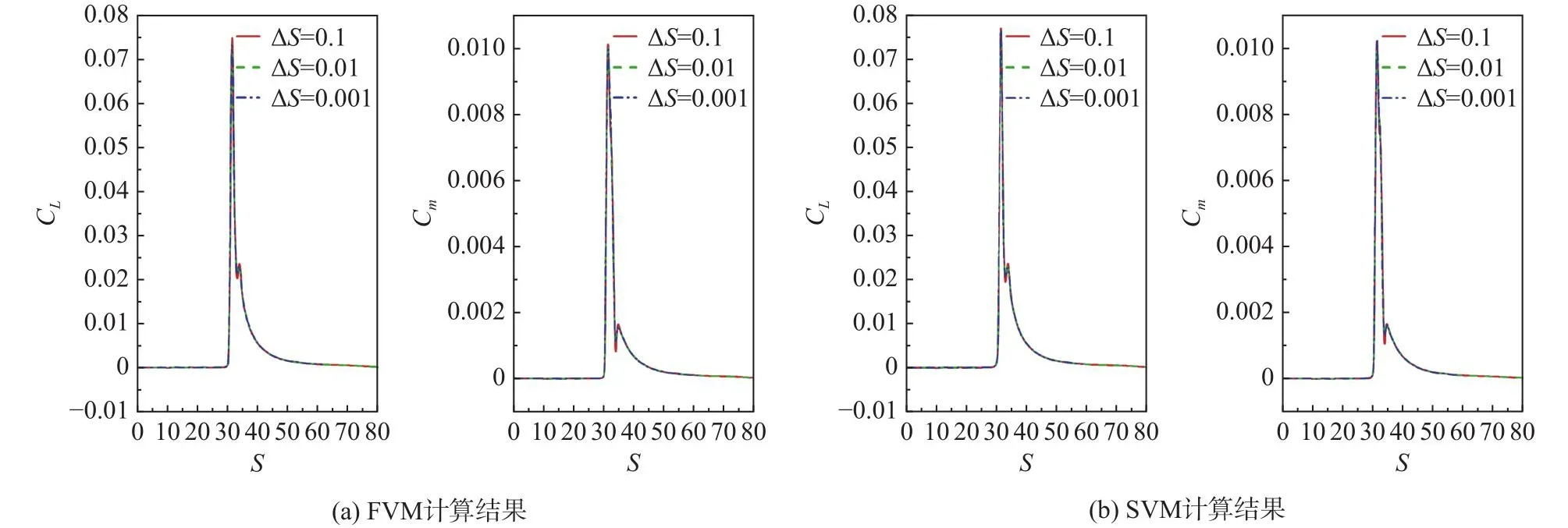
图3 时间步长对FVM和SVM阵风响应的影响Fig.3 Effects of time step on gust response obtained by FVM and SVM

图4比较了阵风尺度为1c时本文计算得到的升力系数阵风响应与文献[8]的结果。对于小尺度阵风，阵风梯度增大、作用域更为集中，在阵风离开翼型后缘的时间段内，升力系数产生小幅波动；除波动幅值存在一定差异外，本文FVM和SVM两种方法计算得到的升力系数峰值及其出现时刻均与文献结果吻合良好。

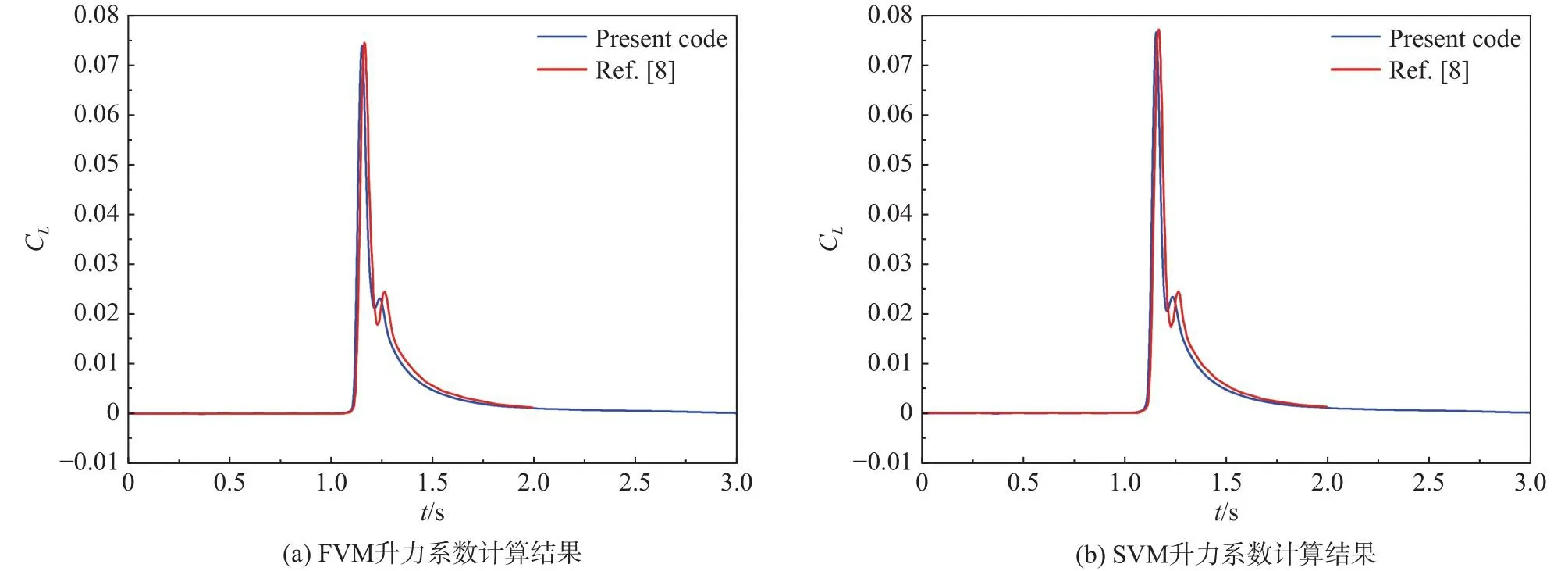
图4 FVM和SVM气动力阵风响应与文献结果对比Fig.4 Comparisons of aerodynamic responses between present and ref.[8]data

进一步研究表明，阵风离开翼型后缘时升力系数小幅波动的幅值与翼型后缘厚度的处理方式直接相关。图5比较了尖后缘和钝后缘NACA0012翼型计算得到的升力系数阵风响应，钝后缘翼型后缘厚度为1.26‰c。相比于尖后缘，阵风离开钝后缘翼型时升力系数响应的波动幅值更大，峰值略微降低。

5.1.2 阵风尺度的影响

分别采用FVM、SVM计算阵风尺度 1c、5c和10c，等效迎角 Δα= 2.0°的阵风响应，计算结果如图6所示。在阵风尺度5c和10c时，FVM和SVM的计算结果几乎一致。当阵风尺度减小到1c时，阵风场的时空导数增大，SVM方法中源项的作用凸显出来，导致FVM和SVM的计算结果出现差异，SVM计算得到的气动参数阵风响应峰值略高于FVM。SVM方法的推导过程表明FVM只是SVM忽略源项的一种近似方法，因此理论上SVM的计算结果更为准确。随着阵风尺度的增加，阵风场的时空导数减小，阵风离开翼型后缘时气动系数的小幅波动现象消失。

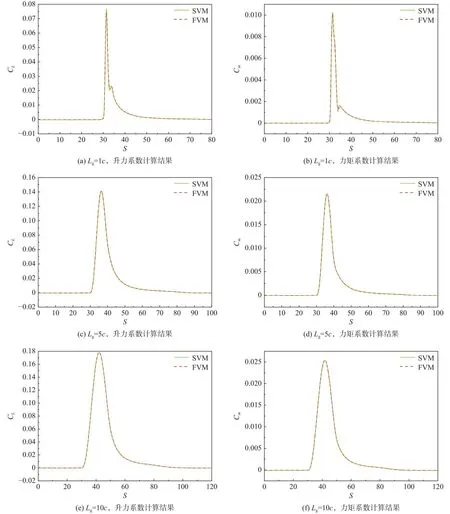
图6 阵风尺度对FVM和SVM的阵风响应影响Fig.6 Gust length effect on gust responses obtained by FVM and SVM

5.1.3 黏性对阵风响应的影响

针对阵风尺度1c和10c、等效迎角 Δα= 2.0°，采用SVM方法开展Euler、N-S方程的阵风响应对比计算，其中N-S方程计算网格的第一层网格高度为1×10-5c，其他网格参数与Euler方程计算网格相同。计算结果对比如图7所示，黏性效应导致阵风响应的升力系数峰值降低，阵风尺度越大，黏性对阵风场的影响越大，升力减小量越明显；黏性作用下，1c阵风离开翼型后缘时的升力系数波动明显减弱。

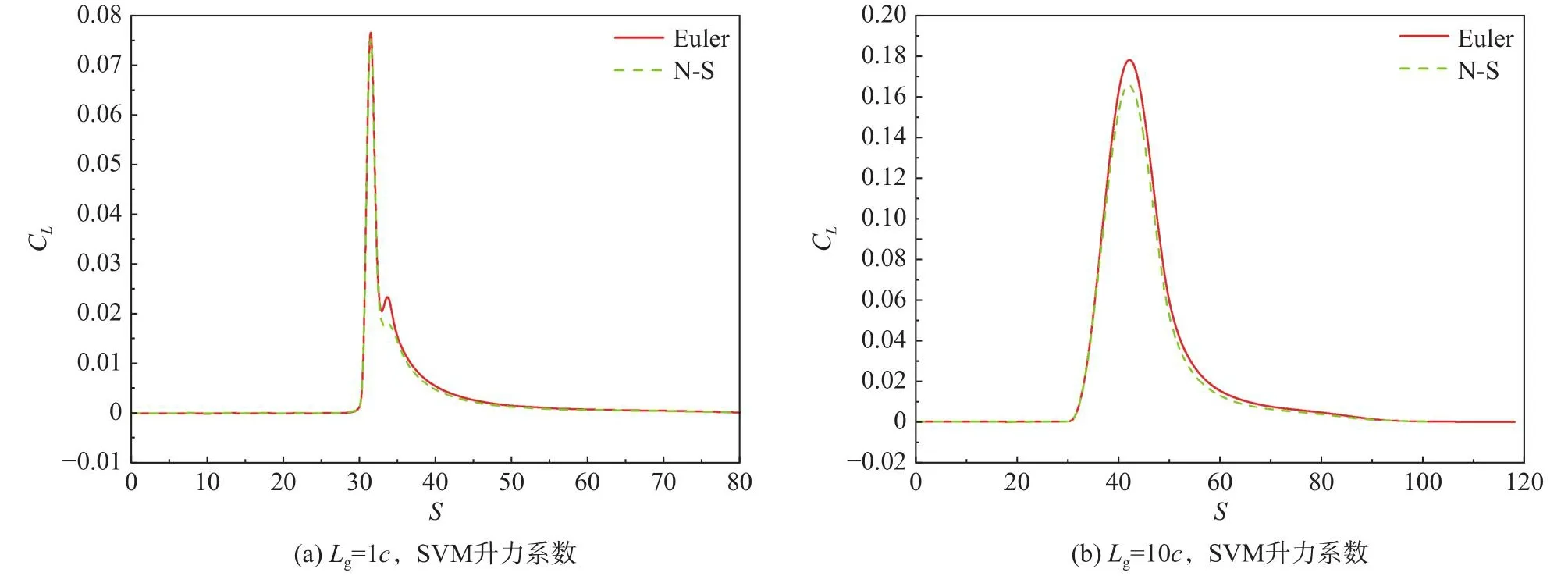
图7 黏性对阵风响应的影响Fig.7 Viscosity effects on gust response

5.2 弹性翼型阵风响应计算

采用非定常Euler方程计算弹性NACA0012翼型的阵风响应。翼型结构模型参数[22]由表1给出。

表1 NACA0012翼型结构参数Table 1 NACA0012 parameters

5.2.1 阵风响应CFD/CSD耦合算法验证

选取文献[22]的计算参数，Ma= 0.3，V*= 0.2，翼型弦长c= 1.0 m。翼型结构位移的初始状态 ξ (0) = 0，α(0)= 0°，阵风尺度Lg= 6.25 m，等效迎角 Δα= 0.57°。考虑到文献计算方法为FVM，本算例也采用FVM。计算结果对比如图8所示。本文计算结果与文献[22]数据吻合，验证了本文弹性翼型阵风响应CFD/CSD耦合算法的可靠性。

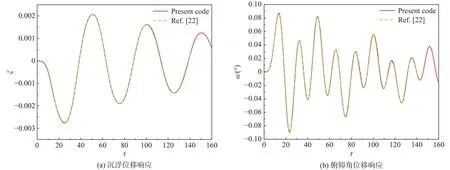
图8 弹性翼型阵风响应与文献结果对比Fig.8 Comparison of gust responses of an elastic airfoil between present and reference results

5.2.2 弹性对翼型阵风响应的影响

采用SVM计算阵风尺度1c和10c、等效迎角 Δα=2.0°的阵风响应，V*= 0.2，翼型结构初始状态 ξ (0) =0，α(0)= 0°。图9为刚性翼型和弹性翼型的气动系数阵风响应对比。图10为弹性翼型的结构响应结果。在One-Minus-Cosine阵风穿越弹性翼型期间，翼型的气动参数和俯仰角均先增大然后减小至极小值，沉浮位移则一直增大至峰值；10c阵风穿越弹性翼型时，升力和俯仰角近乎同时达到峰值，导致升力峰值较刚性翼型增大；1c阵风穿越弹性翼型时，俯仰角峰值远滞后于升力峰值，弹性对升力峰值几乎没有影响。

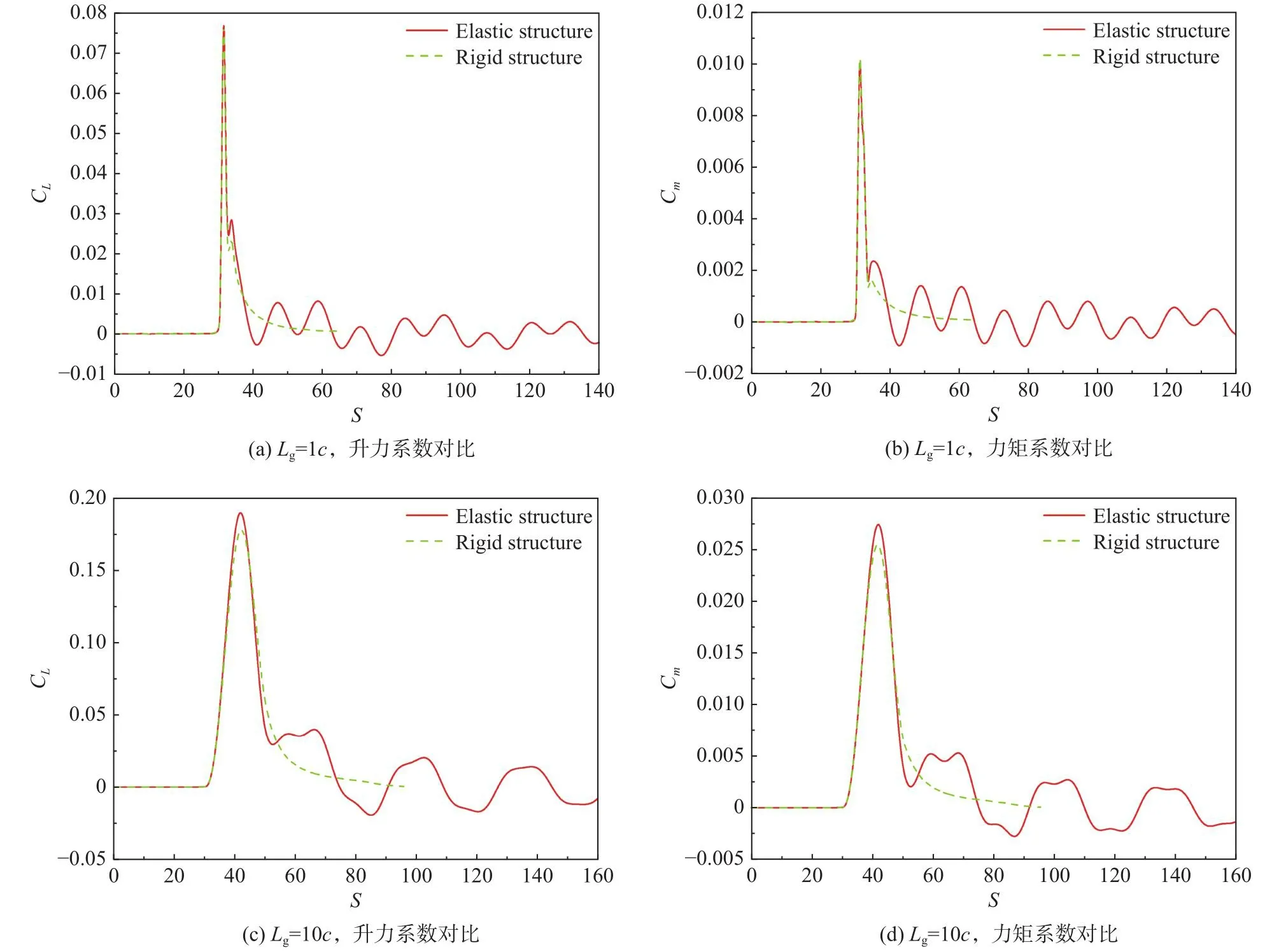
图9 刚性和弹性翼型气动力阵风响应对比Fig.9 Comparison of aerodynamic gust response between rigid and elastic airfoils

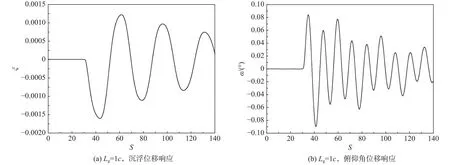
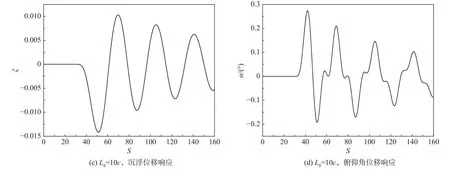
图10 弹性翼型结构响应Fig.10 Structural response of an elastic airfoil

5.3 弹性翼型阵风载荷减缓

以NACA64A010翼型为研究对象，翼型弦长c=1.0 m，其他网格参数与第5.1节Euler方程计算网格相同，如图11所示。翼型结构参数[23]如表2所示，取Ma= 0.3、V*= 0.337 4。采用SVM进行翼型阵风载荷减缓响应计算。阵风尺度Lg= 10c，等效迎角 Δα=2.0°。翼型结构位移 的 初 始状态 ξ (0) = 0、α(0) = 0°、β(0)= 0°。本文以减缓翼型在通过阵风时产生的最大升力系数为目标。

表2 NACA64A010翼型结构参数Table 2 NACA64A010 parameters

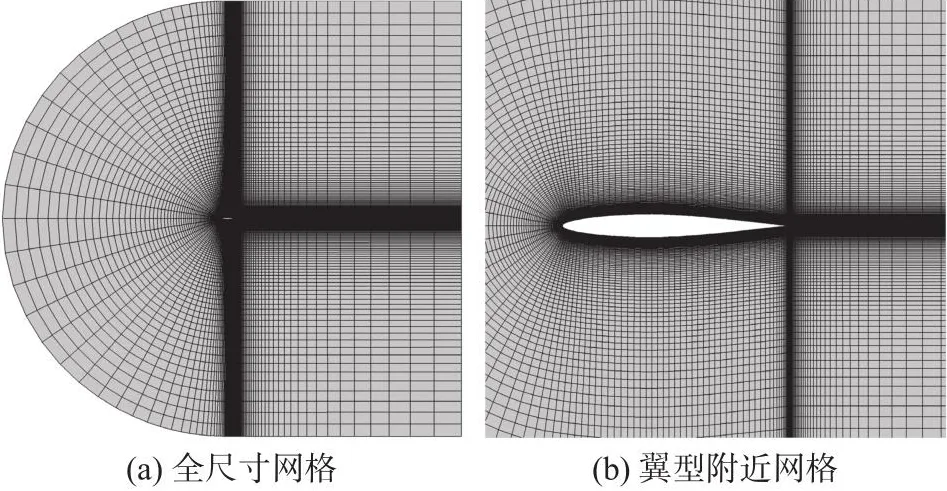
图11 NACA64A010翼型计算网格Fig.11 Computational mesh for NACA64A010

弹性翼型阵风响应分析表明，在阵风穿越翼型期间，升力系数先增大后减小至极小值，而翼型沉浮位移则一直增大至极值，因此本文选取沉浮速度值作为控制输入量。图12、图13为增益G3分别取5.0和10.0时闭环控制系统与开环系统阵风响应的结果对比。采用G3闭环控制情况下，沉浮运动峰值显著降低并迅速收敛；在升力系数峰值之前，由于翼型沉浮速度为负值，G3等效于给弹性翼型增加低头俯仰控制力矩，导致俯仰角、升力和力矩系数峰值明显降低，G3= 10时升力系数峰值降低49.758%；当阵风离开翼型后，翼型沉浮速度为正值，俯仰控制力矩使翼型俯仰角逐渐增大至正极大值点，并高于无控制情况，导致此时气动系数响应极值也均略高于无控制情况，并接近或高于阵风穿越翼型时的峰值。

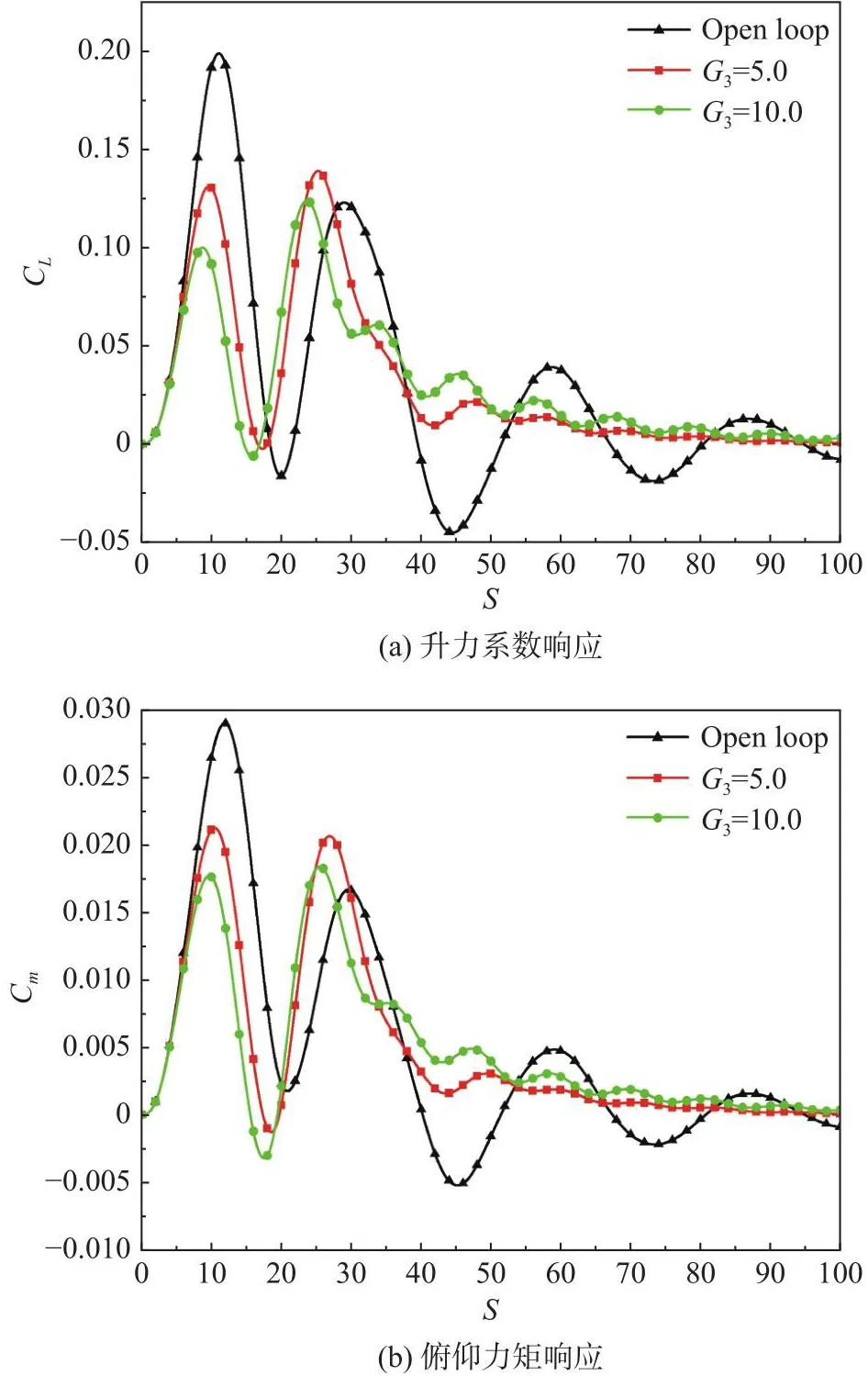
图12 开环系统和闭环控制系统翼型气动力阵风响应对比Fig.12 Comparison of aerodynamic gust responses between open- and closed-loop control systems

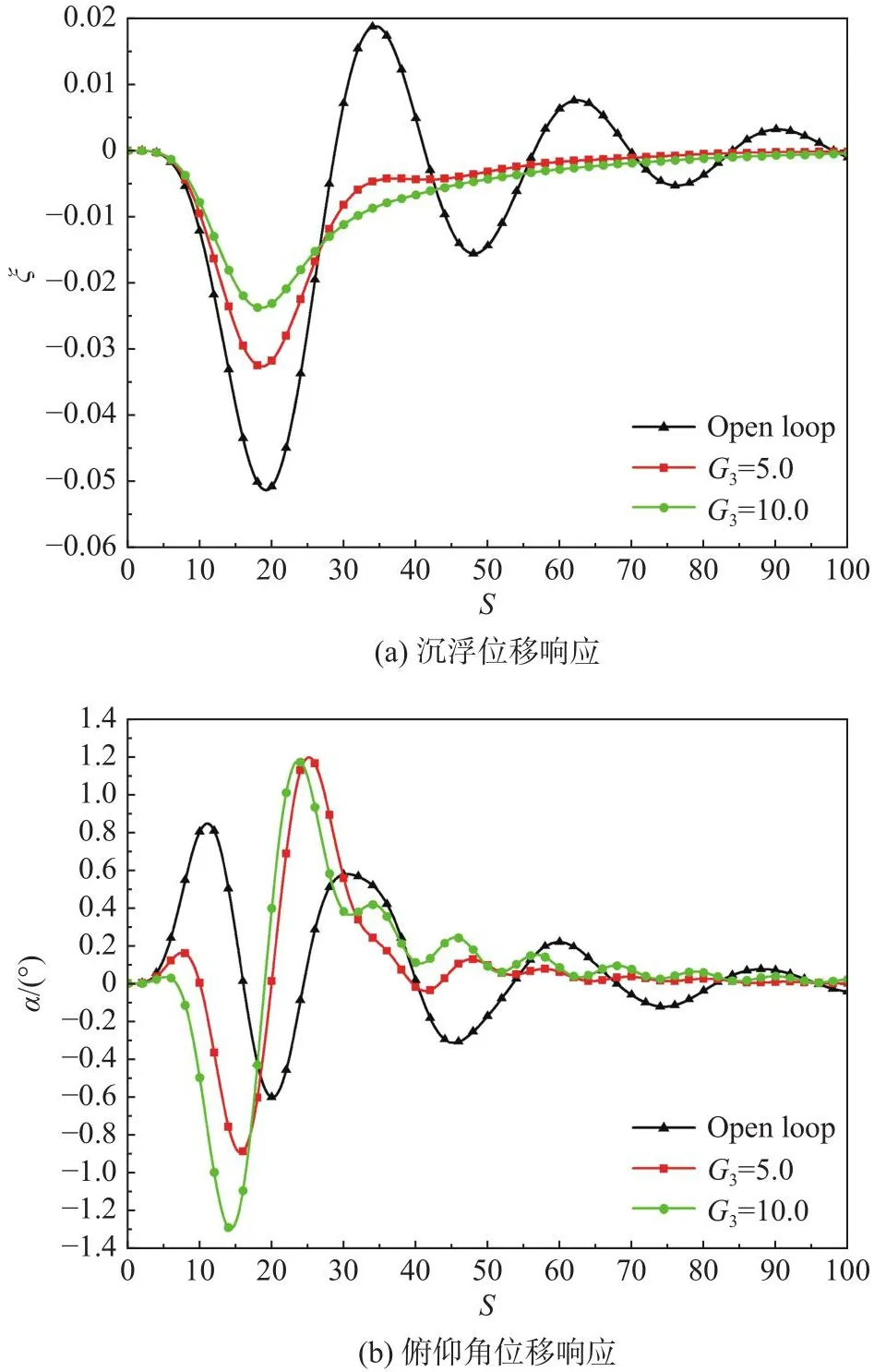
图13 开环系统和闭环控制系统翼型结构响应对比Fig.13 Compsrison of structural response between open- and closed-loop control systems

接下来采用G2= -5.0、G3= 10.0同时控制翼型的沉浮和俯仰运动。图14、图15分别为G2、G3组合的闭环控制阵风响应结果和仅G3的响应结果对比。增加俯仰控制后，俯仰角位移幅值显著减小，导致阵风作用期间的气动参数峰值高于无俯仰控制情况，但阵风离开翼型后的气动参数极值则显著降低。

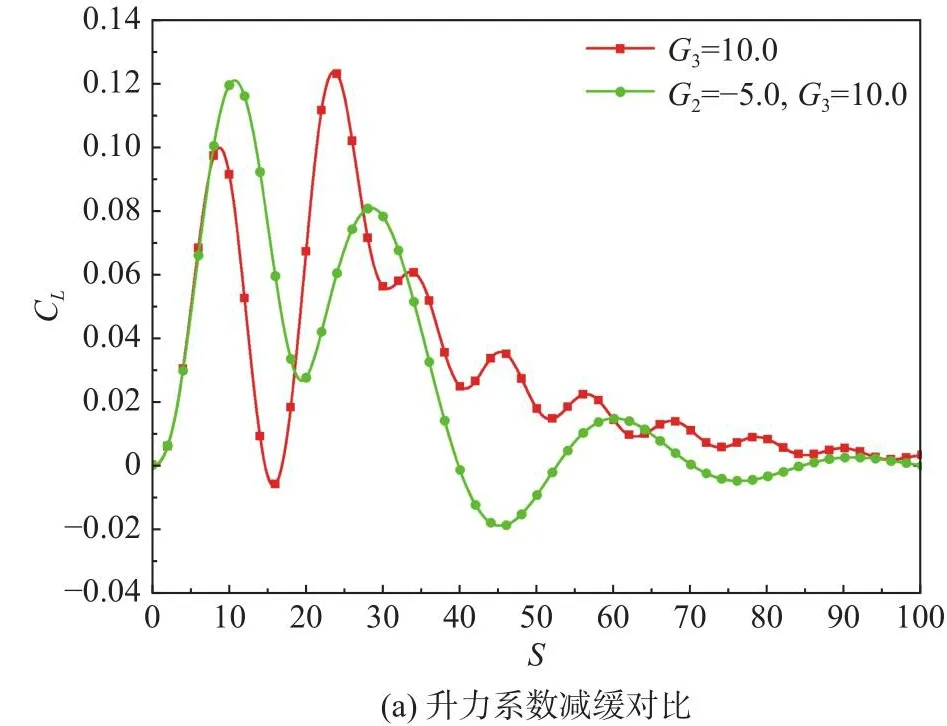
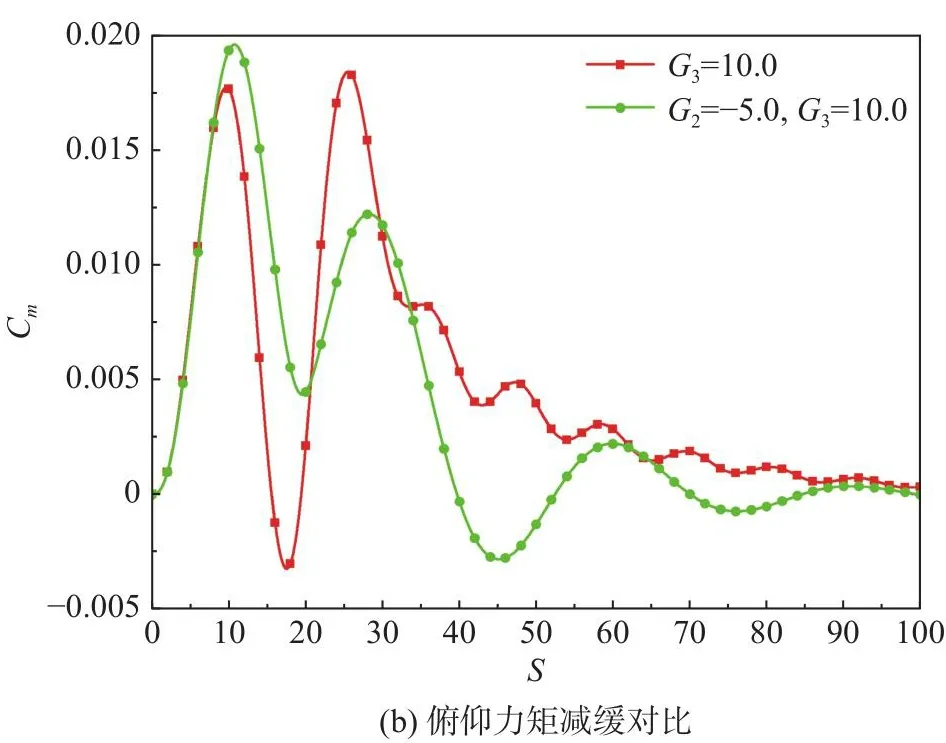
图14 G2 = -5.0、G3 = 10.0和仅有G3 = 10.0气动力响应对比Fig.14 Comparison of aerodynamic response between G2 = -5.0, G3 = 10.0 and only G3 = 10.0

图15 G2 = -5.0、G3 = 10.0和仅有G3 = 10.0结构响应对比Fig.15 Comparison of structural response between G2 = -5.0, G3 = 10.0 and only G3 = 10.0

6 结 论

本文基于动态网格系统下非定常N-S方程，理论推导出SVM阵风模拟的控制方程，发展出基于SVM的弹性翼型阵风响应CFD/CSD时域耦合算法和基于翼型俯仰控制的阵风减缓模拟方法。算例分析了NACA0012刚性、弹性翼型的One-Minus-Cosine阵风响应，计算结果与文献数据吻合；分析了阵风尺度、流体黏性和结构弹性对NACA0012翼型阵风响应的影响；实现了基于俯仰控制的NACA64A010弹性翼型阵风减缓。主要结论如下：

1） 理论推导表明，传统FVM是忽略SVM中阵风相关附加源项的一种近似方法，对于大尺度阵风，两种方法的计算结果一致，源项的作用随着阵风尺度的减小而凸显，理论上SVM更为准确；

2） 黏性效应导致NACA0012翼型升力系数阵风响应峰值降低，阵风尺度越大，升力减小越明显，黏性同时减弱了1c阵风离开翼型后缘时的升力系数波动；

3） 结构弹性引起NACA0012翼型俯仰角阵风响应峰值增加，阵风尺度越大，升力系数增加越显著；

4） 俯仰控制能够有效减缓NACA64A010弹性翼型的阵风载荷，沉浮速度控制输入量G3= 10.0时升力系数阵风响应峰值减缓49.758%，结合G2、G3则能够同时减缓沉浮和俯仰响应。