粗糙元取向对湍流统计量影响的数值研究

李世隆，杨晓雷，*，袁先旭，郭启龙

(1.中国科学院 力学研究所 非线性力学国家重点实验室，北京 100190；2.中国科学院大学 工程科学学院，北京 100049；3.中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000；4.空气动力学国家重点实验室，绵阳 621000)

0 引 言

工程应用中的壁湍流通常发生在具有一定粗糙度的表面[1-4]，例如大气边界层[5-6]、河流[7]、被侵蚀的螺旋桨桨叶绕流[8]。壁湍流对近壁区的动量和能量输运起着至关重要的作用，相关研究可以追溯到Colebrook[9]、Nikuradse[10]和 Moody[11]等学者的经典工作。近期的数值模拟研究采用随机旋转的椭球体作为粗糙元生成粗糙壁表面[12-13]。在本研究中，我们尝试关注椭球体的取向，即椭球粗糙元随机旋转与椭球粗糙元取向一致，如何影响粗糙壁湍流的统计特征。

相比于正弦状[14]和立方体粗糙元[15]生成的粗糙壁，以椭球体作为粗糙元的粗糙壁湍流研究相对较少。本文所采用的椭球体粗糙元最早见于Scotti在2006年发表的文章[16]。该椭球体的三个半轴长分别为r、1.4r和 2r（r为椭球体的最小半轴长）。粗糙壁表面通过将椭球体放置在 2r×2r的方格中，并进行随机旋转获得[16]。Scotti[16]的研究结果显示，在过渡粗糙区，该粗糙壁对应的等效砂粒粗糙度长度ks≈r。针对椭球粗糙壁槽道湍流，Yuan等[17]系统研究了椭球粗糙度对雷诺应力输运特性的影响。Yuan等[12]着重研究了椭球粗糙壁湍流在粗糙子层中的统计特性。Hantsis和Piomelli研究了椭球粗糙度对被动标量输运的影响[18]。针对其他椭球粗糙壁湍流，Yuan和Piomelli研究了该粗糙壁对汇流边界层的积分量、湍动能输运特性、湍流结构的影响[19]，开展了椭球粗糙壁的加速边界层直接数值模拟，发现粗糙壁可以避免加速导致的湍流层流化[20]。Wu等[21]研究了椭球粗糙壁冲击射流的流动特性，并与光滑壁的结果进行了对比。研究者也对比了椭球粗糙壁和其他类型粗糙壁的湍流特性。Jouybari等[22]将椭球粗糙壁的湍流结构与立方体粗糙壁及真实叶片表面粗糙壁的湍流结构进行了对比。Mangavelli等[23]研究了槽道湍流中椭球粗糙度与真实叶片表面粗糙度在脉冲式突然加速情况下的作用。椭球粗糙壁的结果也被用于发展粗糙壁湍流的模型[24-25]及数据驱动的粗糙度长度模型[13]。

为了能够节省计算量，Chung等[26]根据Jiménez和Moin关于光滑壁槽道流的最小槽道的研究[27]，提出了粗糙壁湍流的最小槽道理论。在外层相似性理论的支持下，最小槽道可以较为准确地预测粗糙壁湍流的速度亏损，并发现槽道的展向尺寸为L+z≈350、流向尺寸L+x≈930时，就可以较为准确地预测平均流向速度廓线及流场结构[28]。

椭球粗糙元的取向影响壁面的阻力分布特征和粗糙子层的流动特征。然而，以上使用椭球体作为粗糙元的文献均采用随机旋转的方式生成粗糙壁表面，难以用于研究椭球粗糙元取向的影响。本工作计划采用三种具有一致取向的椭球体生成粗糙表面，开展粗糙壁湍流直接数值模拟，将其统计量与随机旋转椭球体粗糙壁的结果进行对比，研究粗糙元取向对粗糙壁湍流统计特性的影响。

1 数值模拟方法与算例设置

1.1 数值模拟方法

采用计算流体力学程序VFS-Wind 开展本研究相关的模拟。该程序已成功应用于模拟具有复杂几何边界的湍流[29-32]。近期工作中，我们进一步发展了结合清晰界面浸没边界方法和光滑界面浸没边界方法的混合方法，使得VFS-Wind程序可开展复杂边界下颗粒湍流的颗粒解析模拟[33]。需要指出的是，当前工作的模拟只采用了清晰界面浸没边界方法，没有采用上面提及的混合方法。流动的控制方程为不可压Navier-Stokes方程：

其中：i,j=1,2,3；xi和ui代表三个方向的坐标和速度分量；p为压强；υ为运动黏性系数。

曲线浸没边界方法（curvilinear immersed boundary method, CURVIB）[34]用于模拟粗糙壁表面的复杂几何。该方法基于曲线（或笛卡尔）网格模拟流动，采用三角形网格离散复杂几何边界。为了在流动模拟中施加边界条件，将背景网格点标记为流体点和固体点，将至少有一个固体点邻居的流体点进一步标记为浸没边界（immersed boundary, IB）点（如图1黑实点）。进而，在壁法向通过壁面边界条件（如图1中a点）和流体点速度（如图1中c点）构建IB点速度（如图1中b点）ub=ua+uchb/hc，作为边界条件施加给外流，c点的速度由周围的流体点插值得到，其中ua、ub、uc分别是点a、b、c处的速度。

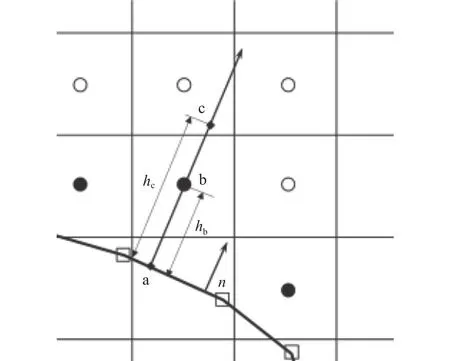
图1 曲线浸没边界方法处理粗糙壁面边界的二维示意图（修改自文献[32]）Fig.1 Treatment of rough surfaces for the CURVIB method(adapted from[32])

1.2 算例设置

以椭球作为粗糙元生成粗糙壁的表面几何，共考虑12种粗糙壁表面。其中包括四种不同的粗糙元取向（随机取向、垂直放置、朝下游倾斜45°、朝上游倾斜45°）。对应每种取向，选取三种不同的流向和展向粗糙元间距（l）。

表1中列出了所有的模拟算例。表中， θz为沿椭球第二长轴（展向方向）旋转的方向，其取值为0°和45°时分别对应图2（a）和图2（b）所示的粗糙元取向，其没有取值时对应图2（c）所示的随机取向。表中，Reτ为基于摩擦速度、槽道高度h和黏性系数的雷诺数。在模拟中，采用定流量的方式驱动槽道湍流，所得雷诺数不完全相同，但基本在1 000附近。

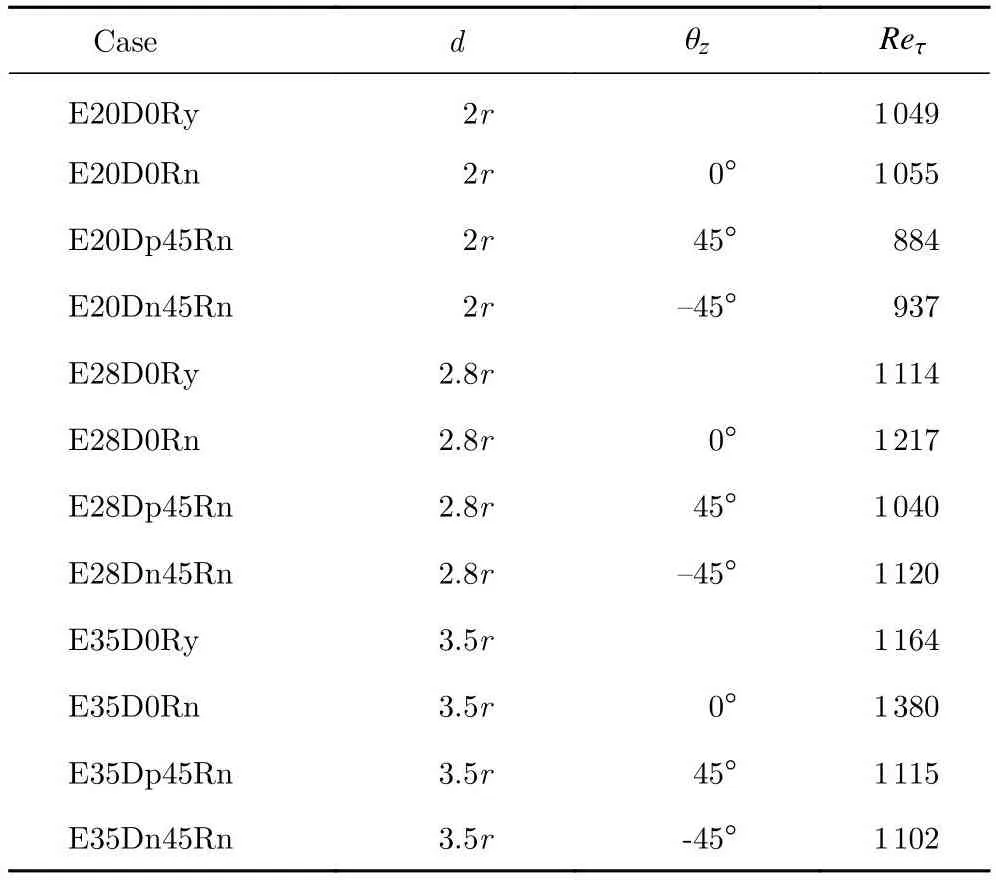
表1 粗糙壁湍流模拟的算例设置Table 1 Numerical setups for simulations of rough-wall turbulence

以下简要说明算例的命名规则。每个算例名称的第一个字母代表粗糙元的形状，即字母“E”代表椭球体。该椭球体半轴分别为r、1.4r、 2r（对于所有模拟算例，r/h=0.07），其中心位于壁面下方z=-0.5r处。第一个字母后面的数字表示粗糙元的间距，例如，E20D0Ry 中的 20 表示l= 2.0r。字母“D”表示粗糙元的取向。字母组合“Rn”（0°）代表粗糙元的初始取向，如图2（a）长轴和短轴分别沿着壁法向方向和流向方向。字母数字组合“p45”和“n45”分别代表椭球粗糙元沿第二长轴（沿展向方向）正向和负向旋转45°，如图2（b）所示。字母组合“Ry”代表椭球的随机旋转，如图2（c）所示。如果椭球较近，则相邻椭球之间允许重合。图3显示了所有模拟粗糙壁表面几何的局部示意图。

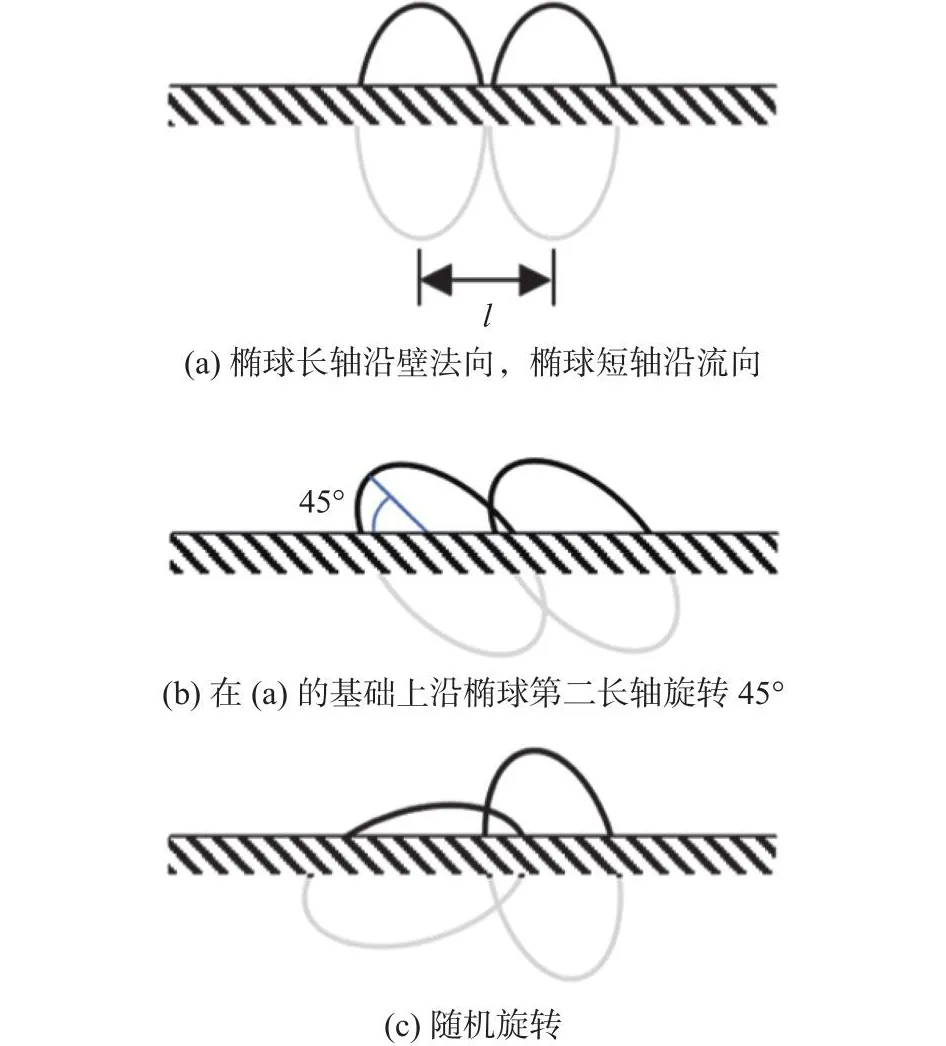
图2 椭球粗糙元取向的示意图Fig.2 Sketch of ellipsoid orientation

图3 粗糙壁几何的局部示意图（所显示区域在流向和展向的尺寸分别为h和 0.5h）Fig.3 Sketch of rough surfaces in an area with size h × 0.5h

采用流向（x）、壁法向（y）和展向（z）尺寸为 3h、h、h的全尺寸槽道，该槽道尺寸小于通常采用的槽道尺寸。但计算域大小仍约为Chung等测试的最小槽道的9倍，在保证解析近壁流场结构和容纳足够多粗糙元的同时，降低了计算量，使得大量不同粗糙壁湍流的直接数值模拟成为可能。小槽道与全尺寸槽道结果的对比见附录。所模拟算例的计算域在流向（x）、壁法向（y）和展向（z）对应的网格节点数分别为513、300和172。离开壁面第一个网格的宽度为其中uτ为摩擦速度。在其他两个方向上，无量纲的网格宽度约为 Δx+=Δz+=6。时间步长为 2 ×10-3h/Ub，其中Ub为流向截面的平均速度。在粗糙壁表面，通过CURVIB方法施加无滑移边界条件，在上边界施加自由滑移边界条件，在水平方向施加周期边界条件。通过在流向施加保证定流量的平均压力梯度驱动流动。在所有模拟中，首先将流场发展至充分发展状态，再求解 6 0h/Ub平均值，计算湍流统计量。

2 模拟结果

本节介绍不同粗糙壁的模拟结果，包括粗糙壁附近的流场结构、平均速度、雷诺应力、分散应力、零平面位移、等效砂粒粗糙度长度等。分散应力描述了时间平均流场在空间上的非均匀程度，通过将瞬时速度ui进行如下分解得到：其 中上 加横 线¯·表 示 时 间 平均，表示水平方向的空间平均。近壁处的空间平均包括固体和流体。

图4显示了不同粗糙壁附近的瞬时流动结构。可以看到，流动结构的复杂性与椭球体取向的随机性密切相关。对于具有相同取向的粗糙元生成的粗糙表面，通常可以观察更为规则的流动结构，例如E20D0Rn、E20Dp45Rn。而对于随机取向椭球体生成的粗糙壁表面，即E20D0Ry、E28D0Ry和E35D0Ry，由于粗糙元周围流动的差异以及相邻粗糙元间的相互作用，可以观察到更为复杂的流动结构。如图4所示，粗糙元周围流动的一个重要特征是流动沿粗糙元迎风面的向上运动。一个有趣的现象是，当椭球体朝上游或朝下游倾斜时，其上方的流动结构具有一定的相似性。当间距较大（l=2.8r，3.5r），椭球体朝下游旋转时（E28Dp45Rn、E35Dp45Rn）的流动结构相较于朝上游旋转时（E28Dn45Rn、E35Dn45Rn）的具有更高幅值的流向速度。

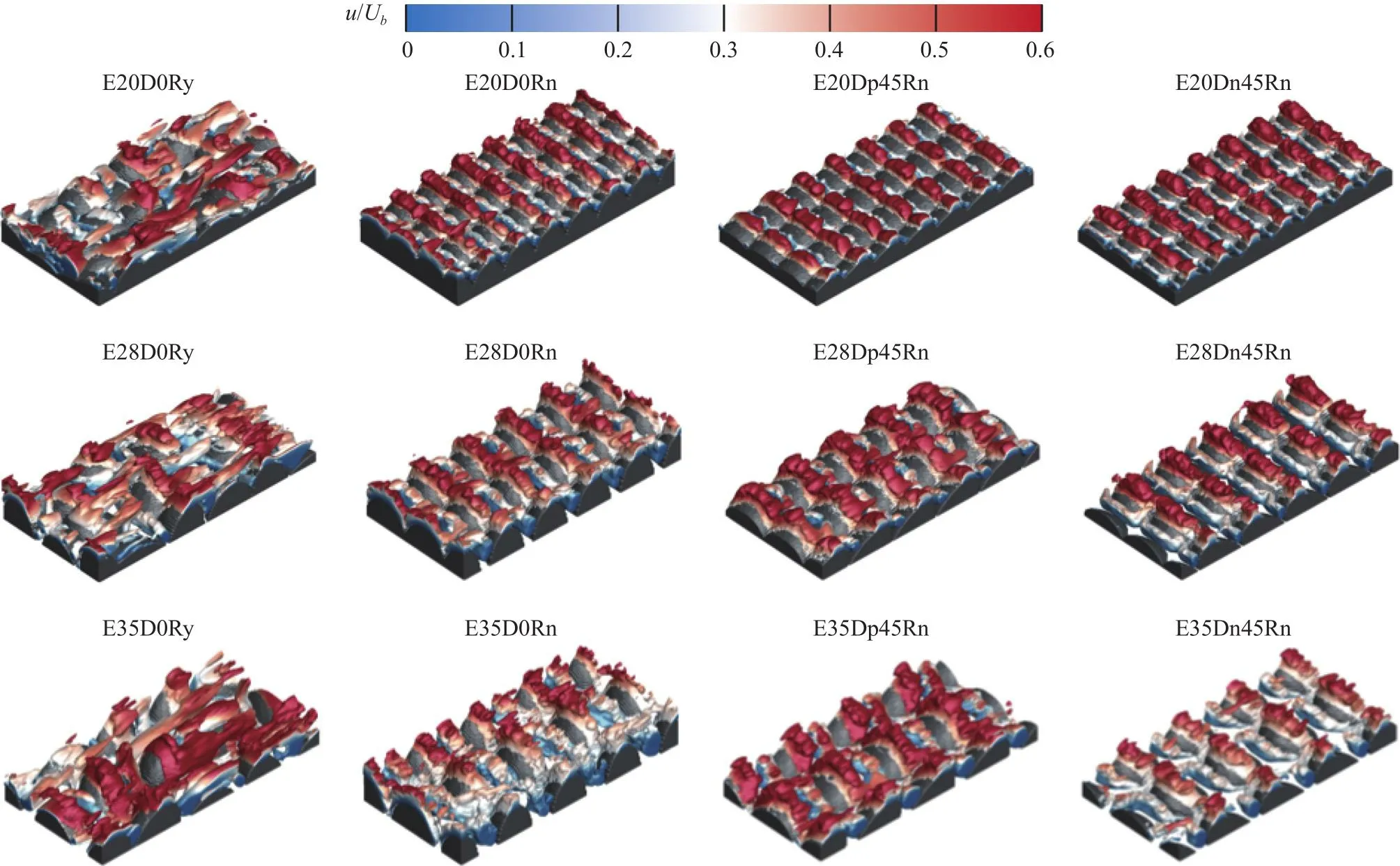
图4 使用 Lambda2 准则（λ2 = -0.5）可视化的近壁流动结构（等值面使用时间平均的流向速度着色，图像中仅显示了 一部分区域）Fig.4 Near-wall flow structures visualized by the λ2-criteria (λ2 = -0.5).Iso-surfaces are colored by the time-averaged streamwise velocity.Only part of the flow filed is shown

为了展示粗糙元尾迹的三维几何特征，图5显示了时间平均流向速度u=0的等值面。可以看到，随机旋转椭球元素尾迹的形状与相同取向椭球体的尾迹形状有显著不同。另一方面，粗糙元间距是影响尾迹形状的关键因素。对于本文所考虑的粗糙元间距，流向速度小于0的尾迹区域都直接作用于下游粗糙单元。在粗糙元间距较小时（l=2.0r，2.8r），相邻行的尾迹区域相互连接；在粗糙元间距较大时（l=3.5r），相邻行的尾迹各自独立。

图5 使用流向速度u = 0 等值面标记的尾迹形状（为清晰起见，未显示粗糙度单元表面的等值面）Fig.5 Wake shapes illustrated by u = 0.The iso-surface u = 0 at the surface of the roughness element is not shown for clarity

图6显示了不同粗糙壁算例的平均流向速度廓线。可以看到，所有算例都具有一个清晰的对数区域。在该区域，粗糙壁的流向速度低于光滑壁，该速度差被称为粗糙度函数ΔU。图6显示，当粗糙度单元间距为 2.0r时，随机旋转椭球粗糙壁（E20D0Ry）的ΔU高于其他算例；而对于高一些的粗糙元间距（l=2.8r，3.5r），垂直放置椭球粗糙壁（E28D0Rn、E35D0Rn）的ΔU高于其他算例。当以相同的方式朝上游或下游倾斜椭球体时，粗糙度函数比垂直放置的有所降低（例如，E20Dp45Rn或E20Dn45Rn与E20D0Rn相比）。一个有趣的现象是，椭球朝上游倾斜（E20Dn45Rn）时的 ΔU与朝下游倾斜（E20Dp45Rn）时的ΔU基本相同。对于所有粗糙元取向，ΔU均随粗糙元间距增加而增加。

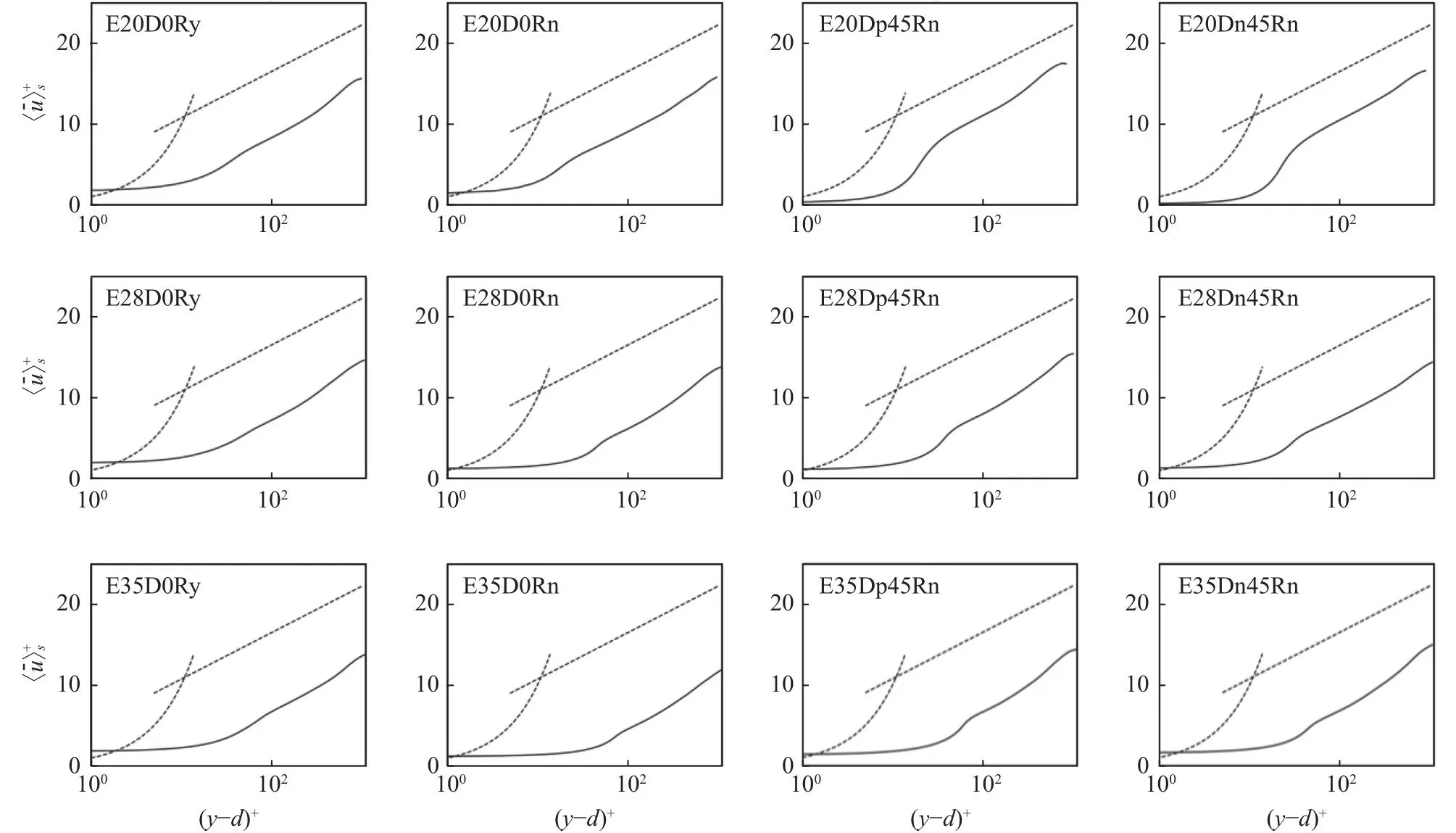
图6 不同粗糙表面的平均流向速度廓线（虚线为光滑壁的线性律和对数律，不同粗糙壁参数见表1）Fig.6 Vertical profiles of the mean streamwise velocity computed from cases with different rough surfaces.The dashed lines show the linear profile and the logarithmic law for smooth walls.Parameters of rough walls are shown in Table 1

图7和图8定量考察了砂粒粗糙度ks和零平面位移d随粗糙元间距l的变化规律。零平面位移是指平均流向速度为零的位置，代表粗糙壁面对边界层的抬升作用，实际中可能并不准确是速度为零的位置[6]。这里，基于对数律计算d和ks的值，即，8.5，其中U+为通过壁面摩擦速度无量纲化的平均流向速度， κ =0.4 为卡门常数。可将对数率化为y=kseκ(U+-8.5)+d， 这 是 关 于ks和d的 线 性 式 。 将0.15＜y＜0.3之间约20个数据点的y与U+作为观测数据，将ks与d作为优化参数，可以得到与对数率较为符合的ks与d。壁面摩擦速度通过驱动流动的流向平均压力梯度计算获得。在图7中可以看到，由于椭球粗糙表面迎着正流向速度的面积增加，ks随着单元间距的增加而增加。椭球垂直放置粗糙壁的增长率最高，而椭球随机取向壁面的增长率最低。另一方面，朝上游和朝下游倾斜椭球壁面的ks和增长率大致相同。间距为 2.8r或 3.5r时，椭球垂直放置粗糙壁的ks值高于其他椭球取向粗糙壁。

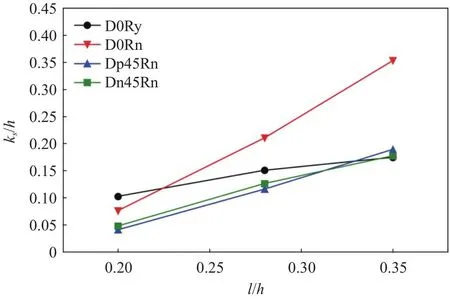
图7 砂粒粗糙度 ks 随粗糙元间距的变化Fig.7 Variations of sandgrain roughnessks with roughness element spacing

图8 零平面位移 d 随粗糙元间距的变化Fig.8 Variations of zero-plane displacementd with element spacing

不同椭球粗糙壁的零平面位移d随粗糙元间距l的变化如图8所示。可以看到，d值随l的增加而减小。在所有椭球粗糙壁中，垂直取向椭球粗糙壁的d值最大。一个有趣的现象是，当粗糙度间距为 2.8r或3.5r时，椭球朝上游倾斜粗糙壁的d值高于椭球朝下游倾斜粗糙壁，而ks值基本相同。

图9比较了不同椭球粗糙壁的雷诺正应力，不同粗糙壁参数见表1。可以看到，雷诺正应力的三个分量按大小从高到低依次为的最大值位于靠近粗糙壁的位置，而的最大值位置离粗糙壁稍远。对于不同粗糙元间距，不同粗糙壁的和的最大值相近，而的最大值随粗糙元间距增加而减小。与随机取向椭球粗糙壁相比，相同取向椭球粗糙壁的雷诺正应力的峰值更高。朝上游和下游倾斜椭球粗糙壁的峰值基本相同，且高于其他粗糙壁的。图10显示了不同粗糙壁面的流向分散应力。流向分散应力的峰值幅值比其他两个分量高约一个数量级。分散应力衡量了时间平均速度场的空间不均匀程度。可以看到，不同粗糙壁的分散应力有显著差异。在粗糙元间距为 2.0r、 3.5r时，与椭球体垂直放置的粗糙壁相比（E20D0Ry、E20D0Rn），随机旋转椭球体粗糙壁的的最大值更高；在粗糙度单元间距为2.8r时，其最大值基本相同。由图9可见，椭球体朝上游和下游倾斜45°粗糙壁的雷诺应力大致相同（例如E20Dp45Rn 与 E20Dn45Rn）。另一方面，图10显示，其对分散应力的影响是不同的：当朝下游倾斜45°时，的最大值增加（E20Dp45Rn）；而在朝上游倾斜45°时，的最大值降低（E20Dn45Rn）。在增加粗糙元间距时，朝上游倾斜45°时的的最大值幅值逐步增大，而对于其他椭球取向粗糙壁，的最大值幅值增大或减小的趋势并不一致。其原因可能在于，朝上游或朝下游倾斜45°的影响主要局限于粗糙子区，使得分散应力有较大不同。而对于外区流动，两种粗糙壁的平均高度相同，正面密实度和水平密实度也相同，使得水平方向平均的湍流统计量较为接近。另一方面，对于所有椭球粗糙壁，具有较大幅值的范围均随粗糙元间距的增大而逐步增大。

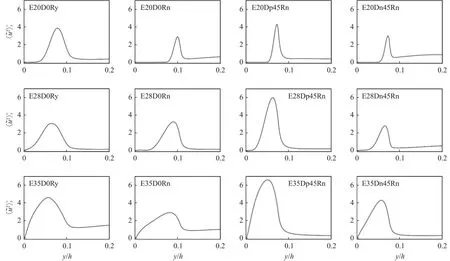
图10 不同粗糙表面的流向分散应力的垂向分布Fig.10 Vertical profiles of the streamwise dispersive stress computed from cases with different rough surfaces

图11 不同粗糙表面的垂向和横向分散应力的垂向分布Fig.11 Vertical profiles of the vertical and spanwise dispersive stresses computed from the cases with different rough surfaces

3 结 论

开展了以椭球体作为粗糙元的粗糙壁槽道湍流直接数值模拟，研究了椭球体取向对粗糙壁槽道湍流统计特性的影响。研究得到以下结论：

1）直接模拟结果显示粗糙元取向对湍流统计量有显著影响。对于小粗糙元间距（l=2.0r，r为椭球体的最小半轴长），随机取向粗糙壁的砂粒粗糙度长度ks高于其他相同取向的粗糙壁；对于大粗糙元间距（l=2.8r，3.5r），垂直放置粗糙壁的ks高于其他粗糙壁。

2）将粗糙元朝上游/下游倾斜45°时的ks基本相同，并且这两种粗糙壁的雷诺正应力（以壁面摩擦速度无量纲化）也基本相同，且高于其他粗糙壁。

3）粗糙元朝上游/下游倾斜45°时的粗糙壁的流向分散应力显著不同，其中，粗糙元朝下游倾斜45°时的流向分散应力更高，且远高于其他粗糙壁。

4）对于零平面位移，垂直放置椭球粗糙壁的值明显高于其他粗糙壁。增加粗糙元间距，粗糙壁的流向雷诺正应力的最大值逐步降低，而其他方向的雷诺正应力没有明显的一致性趋势。

5）对于垂直取向粗糙壁，流向分散应力随着粗糙元的间距增加而增加；对于其他粗糙壁，没有发现随粗糙元间距变化的单调变化趋势。

6）垂向和横向分散应力小于流向分散应力近一个数量级。随机取向椭球粗糙壁的垂向和横向分散应力显著高于其他由相同取向椭球体形成的粗糙壁。

本文研究了粗糙元取向对粗糙壁槽道湍流统计量的影响。更为深入的机理研究及基于这些机理研究发展粗糙壁湍流的工程模型将在未来工作中开展，并将进一步探索不同粗糙壁是否存在统一的标度形式。

附录A 槽道尺寸验证

本附录给出E20D0Ry小槽道模拟结果与全尺寸槽道结果的对比。图A1为小槽道和全尺寸槽道的粗糙壁表面示意图。全尺寸槽道的流向、壁法向、展向尺寸分别为6h、h、3h，对应的网格数分别为1 025、300、513。

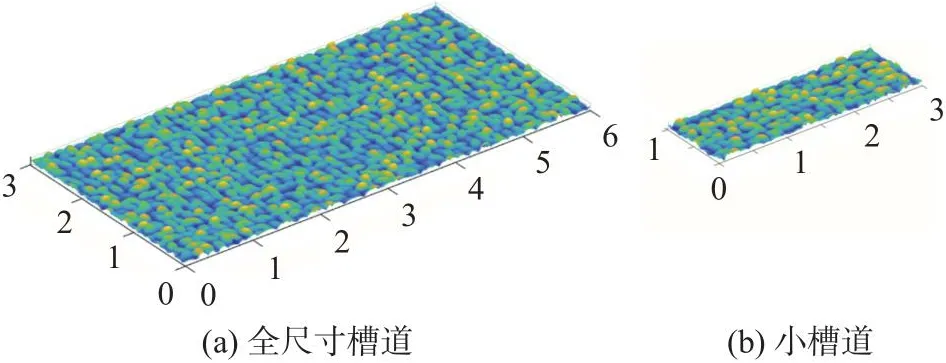
图 A1 全尺寸槽道与小槽道的粗糙壁表面示意图（使用粗糙壁面的高度染色）Fig.A1 Sketch of the rough surfaces (colored by height)for the full-size channel and minimal channel

图A2对比了得到的平均速度廓线、雷诺应力和分散应力。可以看到，平均速度廓线在对数区吻合较好，而在接近槽道中心处，小槽道预测平均速度廓线略高。在近壁面，平均流向速度廓线、雷诺应力和分散应力有一定的差别。

以下，尝试分析产生上述差别的原因。对于槽道中心处平均速度廓线的差别，小槽道在水平方向的尺寸有较大影响。对于近壁面的平均速度和湍流统计量差别，粗糙壁表面统计量的差别可能是主要原因。E20D0Ry粗糙壁面由随机旋转椭球组成，而小槽道中包含的粗糙元个数较少，使得其统计量难以与全尺寸槽道粗糙表面一致。以粗糙壁面平均高度k¯为例，全尺寸槽道k¯ =0.047h，而小槽道k¯ =0.052h。为了定量评估k¯的差异的影响，检查了等效砂粒粗糙度长度和最大流向雷诺正应力随k¯的变化。其中，所采用的Yuan和Piomelli[17]的结果来自于以同样方式生成的粗糙壁表面的槽道湍流直接数值模拟。在他们的工作中，壁面的复杂几何形状采用VOF（volume of fluid）方法处理。从图A3可以看到，等效沙粒粗糙度长度ks和最大流向雷诺正应力基本符合全尺寸槽道结果的变化趋势。从而证明，k¯是造成上述差别的主要原因。对于其他两个方向的雷诺正应力和雷诺剪切应力，小尺寸槽道和全尺寸槽道结果的差别相对较小。对于分散正应力，流向和展向分量的差异相对较大。差异主要体现在小槽道的峰值较小，位置离壁面较远，这与小槽道k¯ 较大是一致的。综上，小尺寸槽道可以较准确地预测近壁面和对数区的流动，可以用于本文的相关研究。

图 A2 小槽道与全尺寸槽道湍流的结果对比Fig.A2 Comparisons between minimal and full-size channels

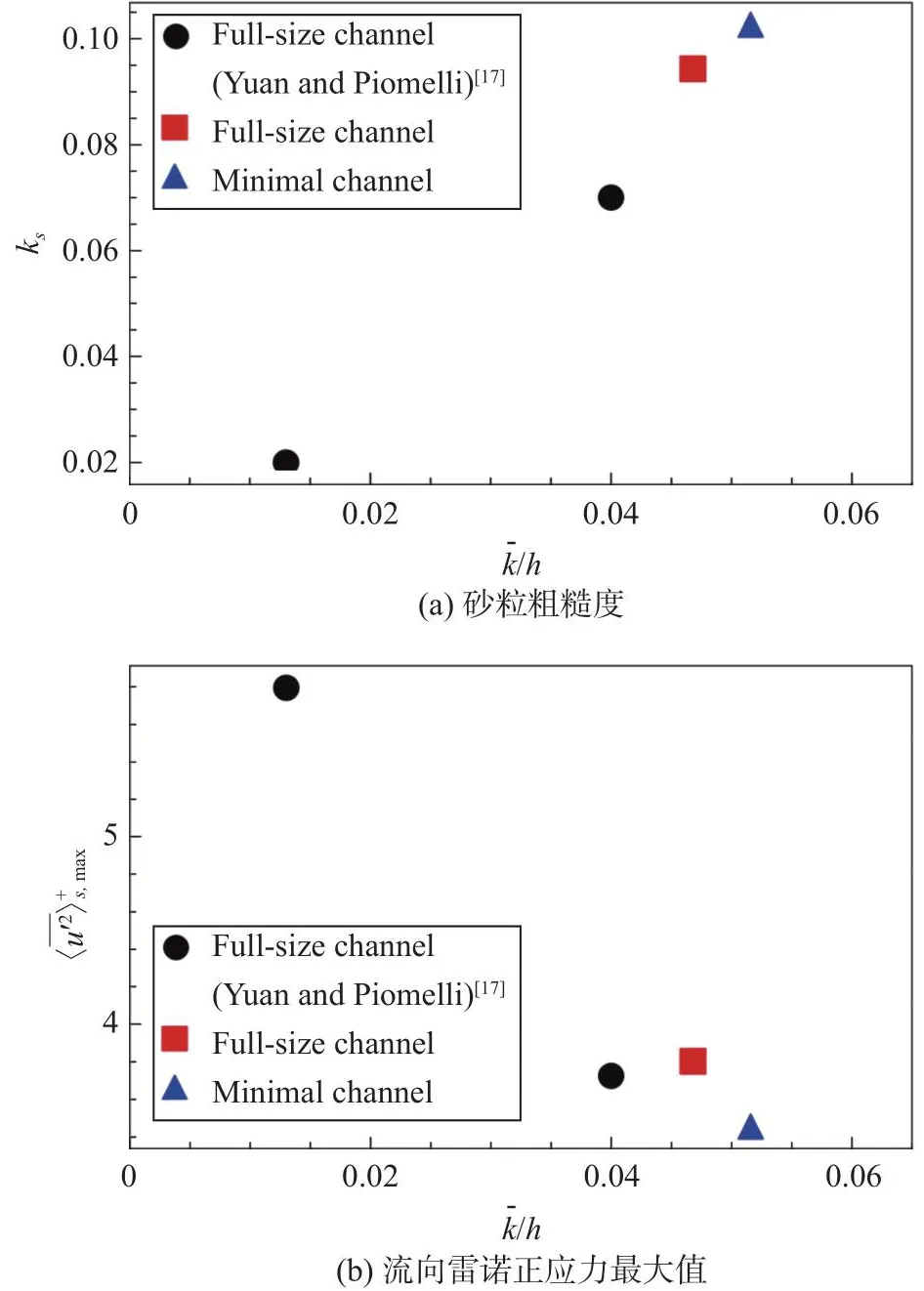
图 A3 砂粒粗糙度和流向雷诺正应力最大值随粗糙壁面平均高度的变化（黑色圆点为Yuan和Piomelli[17]不同椭球半径的结果，红色方块为全尺寸槽道的结果，蓝色三角为小槽道的结果）Fig.A3 Variations of equivalent sandgrain roughness length and the maximum value of the streamwise Reynolds normal stress with the average height of rough surfaces.Black circles sare the results from Yuan and Piomelli[17] of different semi-axis lengths,red squares and blue triangles are respectively the results from full-size and minimal channels