低声爆超声速客机声爆预测及不确定度量化分析
陈树生,顾奕然,杨 华,黄江涛,高正红,*
(1.西北工业大学 航空学院,西安 710072;2.中航工业 第一飞机设计研究院,西安 710089;3.中国空气动力研究与发展中心,绵阳 621000)
0 引 言
随着全球化的发展,利用超声速客机可以极大缩短国际航线的飞行时间,积极发展新一代超声速客机,有望极大促进我国同世界各国在经济、文化等各领域的交流与合作,促进全球化进程不断深入。
为了充分发挥超声速客机的速度优势,未来的超声速客机必须具备陆地上空超声速巡航能力。但超声速客机投入运营仍存在种种阻碍因素,其中声爆噪声显得尤为突出。因此低声爆/低噪声成为未来超声速客机的重要设计指标之一。
20世纪50年代 ,声爆现象首次得到关注,相关研究人员对其开展了初步研究。Whitham针对此现象,首次提出了基于线化理论的声爆预测方法[1]。在1965~1970年间,NASA举办了三届声爆研讨会[2-4],借此推动深刻理解声爆的产生、传播、预测和最小化问题。
21世纪,声爆预测和低声爆超声速客机的研究在国际上重新掀起热潮。2014年,AIAA举办了第一届声爆预测研讨会[5],评估了当前近场声爆信号的计算精度,为远场声爆预测打下基础。2017年,AIAA举办了第二届声爆预测研讨会[6],该研讨会同时将近场过压值信号的计算和远场地面波形的预测作为重点。2020年,AIAA举办了第三届声爆预测研讨会[7-8],该研讨会主要将C608低声爆超声速飞行器作为标准算例,讨论先进的近场CFD声爆信号预测方法及远场地面波形预测方法,及其在具有复杂推进和环境控制系统条件下的低声爆外形计算中的适应性。
目前对声爆的研究主要包括两方面,声爆预测以及低声爆设计。其中声爆预测是指对飞机超声速飞行时产生的声爆水平进行评估,包括对近场、中场以及远场地面的声爆水平进行计算[7-9]。而低声爆设计是指通过一定的方式对飞行器超声速飞行时的声爆水平进行控制,使其处于能够接受的范围[10]。
声爆预测方法大致分为三类:基于线性理论的声爆快速预测方法[11];基于近场CFD与远场非线性传播方程的声爆高精度预测方法[12]以及全场CFD数值模拟方法[13]。其中,基于近场CFD与远场非线性传播方程的声爆高精度预测方法是当前更为合适的声爆预测方法,其优势在于:一是相比于线性理论,该方法能够计算复杂外形的声爆特征,同时结合增广Burgers方程还可以较准确地计算声爆的上升时间;二是相对于全场CFD数值模拟,该方法大大降低了计算量,同时还合理地考虑了真实大气环境中的分子弛豫、热黏性吸收等效应。
近年来,声爆的相关研究在国内也逐渐得到重视。朱自强和兰世隆[14]指出,高精度流场模拟和基于非线性声学的增广Burgers方程等方法在声爆预测中的优势。张绎典等[15]建立了增广Burgers方程的数值求解方法,并提出了一些方法来提高过压值、上升时间等关键参数的计算精度。
超声速客机在飞行过程中,由于飞行高度和大气密度等经常发生波动,大气来流条件也随之不断发生变化。为得到更可靠的低声爆近/远场信号预测结果,在考虑计算网格、物理模型及相对湿度等对声爆近/远场信号预测的影响的基础上, 也需要考虑来流参数的不确定性和由此带来的声爆近/远场信号预测的不确定度。目前,国内外对于考虑来流不确定性的低声爆超声速客机近/远场信号预测的相关研究还较少。
针对CFD不确定度量化分析问题,多项式混沌方法[16]得到了广泛应用。本文拟采用基于非嵌入式多项式的混沌方法(non-intrusive polynomial chaos, NIPC)开展不确定度量化分析研究,即选择一组正交多项式作为空间的无限基函数,将变量分解为确定和随机两部分,从而构造出多项式混沌展开式。该方法将CFD求解器当做黑盒子,基于确定性的解来近似多项式混沌展开式的系数,并在非嵌入式多项式混沌方法的基础上,采用Sobol指数来衡量输入变量的敏感性。
本文拟以AIAA第三届声爆预测会标模C608低声爆超声速飞行器[8,17]为研究对象,开展复杂外形声爆近/远场信号特征分析及不确定度量化分析,以期为超声速客机低声爆设计提供参考依据,并进一步用于超声速客机的鲁棒优化设计及可靠性分析。
1 数值方法
1.1 声爆近场预测方法
在声爆计算体系下,采用基于Naiver-Stokes方程的CFD方法来计算近场过压值分布,从而为声爆传播方程提供输入信号以计算远场地面信号。
在笛卡尔坐标系下,同时忽略体积力(如重力、电磁力等)和外部热源,守恒形式的三维非定常可压缩Naiver-Stokes方程可表示为[18]:
式中:Q为 守恒变量;f、g、h分别为三个坐标方向的通量,可表示为:
式中:ρ为密度;u、v、w为笛卡尔坐标系下的速度分量; τxx、τyy、τzz、τxy、τxz、τyz为黏性应力项;e为单位质量气体的总能量;p为压力;qx、qy、qz分别为三个坐标方向的热流量。
1.2 声爆远场预测方法
在声爆计算体系下,采用基于非线性声学理论的增广Burgers方程方法将近场波形推进到远场,从而求解地面声爆信号。
20世纪60年代,Blackstock[19]最早使用Burgers方程来模拟波在有损耗介质中的传播,提出了经典Burgers方程[20],其形式如下:
在经典Burgers方程中加入非均匀介质、几何扩散以及分子弛豫效应的影响,即可得到增广Burgers方程[21]:
式中:S为声管面积[22];(Δc)v为分子弛豫效应造成的声速变化量; τv为弛豫时间,下标v表示不同的大气组分(如 O2、N2)的弛豫过程。式(7)等号右边 5 项分别对应非线性效应、经典吸收、大气分层、几何扩散以及分子弛豫效应对声爆的影响。
为了便于求解,对式(7)进行无量纲化处理:
式中:P=p′/p0,p0为参考气压;无量纲距离 σ =¯,参考距离为无量纲时间 τ =ω0t′,参考时间为1 / ω0,可由输入信号采样率决定;无量纲耗散参数 Γ =bω0/(2βp0);无量纲弛豫时间 θv= ω0τv;无量纲弛豫系数
1.3 混沌多项式不确定性分析
在考虑来流不确定性的低声爆超声速客机近/远场信号不确定度量化分析中,以地面波形过压值Δp等声爆重要参数作为随机输出变量,表示为:
式中:α*是CFD方法或增广Burgers方程计算结果;αj(x)是计算结果的确定部分耦合系数;随机部分ψj(ξ)是以n维随机变量 ξ =(ξ1,···,ξn)为自变量的随机函数,为 ξ的正交多项式。式(9)可将任一随机变量分解为确定和随机两个独立部分。
出于计算量的考虑,对 ψj(ξ)多项式采取r阶截断,设随机参数的维数为n,则混沌多项式(PCE)项数可以表示为[23]:
根据随机变量 ξ的分布,即输入参数的分布类型不同,对随机变量 ψj(ξ)选取不同形式的正交多项式。当输入参数服从正态分布时,选取Hermite正交多项式;当输入参数服从均匀分布时,选取Legendre正交多项式[23]。
目前,主要有两种形式的基于非嵌入式混沌多项式(NIPC)的不确定度分析方法:随机响应面法(stochastic response surface method, SRSM)和基于Galerkin的投影法。本文采用随机响应面法来求解正交多项式系数,开展不确定度分析。
通常采用过采样策略。文献[24]中推荐选用PCE系数两倍的过采样方法,即N=2Nt=2(R+1)。根据Schaefer等[25]的比较结果,采用精度和收敛性均表现较好的拉丁超立方(Latin hypercube design,LHD)抽样方法,对模型参数进行抽样选取。
定义
利用线性最小二次回归,使J(α)最小,求解得到PCE系数αj的值,同时可以由展开式系数直接计算输出响应的均值 µ和方差D等概率统计量,如下所示:
使用敏感度指标来表征不同随机输入对模型响应输出的影响程度。本文采用可以直接从多项式混沌展开式中得到的Sobol敏感度指标,开展基于方差分解的全局敏感度分析。
将多项式混沌展开式重新分解,得到总方差为:
部分方差为:
则Sobol指数作为敏感性指数定义为部分方差与总方差的比值:
另外,针对输入参数i的Sobol指数(STi)则定义为包含变量i的所有部分Sobol指数之和:
Sobol指数的详细推导过程和具体形式可以参阅文献[26]。
2 模型介绍及程序验证
2.1 C608飞行器外形及来流条件
采用美国AIAA第三届声爆预测研讨会(SBPW-3,2020)提供的C608飞行器标准算例开展研究[7]。C608是NASA低声爆试验飞行器X59的初步改形方案,其来自于洛克希德·马丁公司对NASA N+2超声速客机概念设计研究。三维视图如图1所示。

图1 C608三维视图Fig.1 Three-dimensional views of C608
C608飞行器参考长度L= 27.432 m,半模参考面积s= 37.16 m2,来流条件和边界条件如表1所示。C608具有推进和环境控制系统(environmental control system, ECS)。
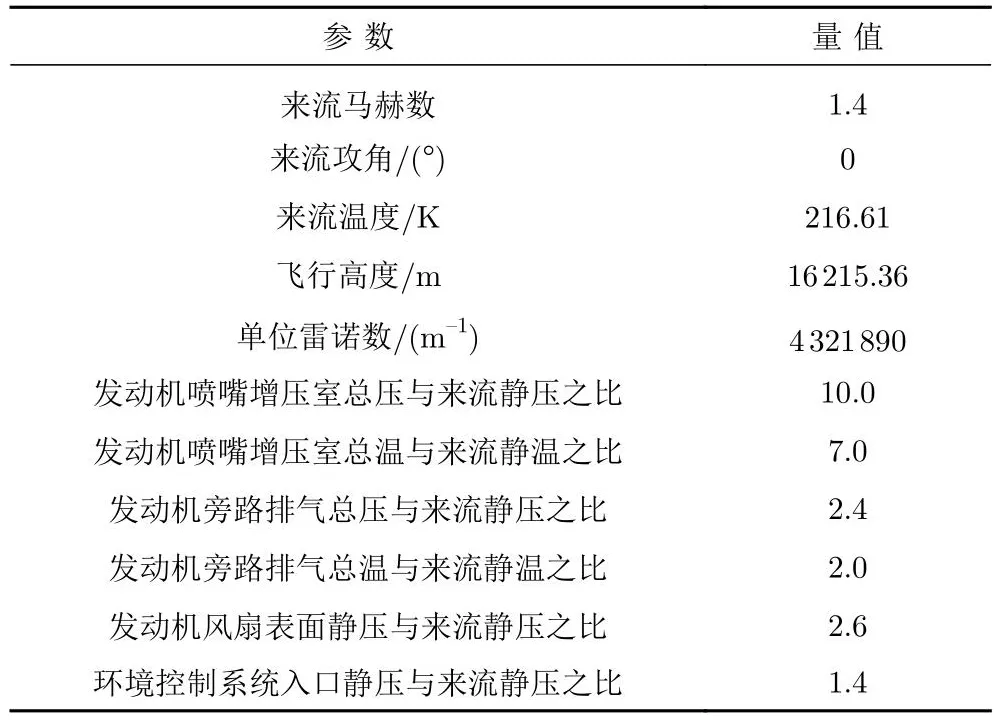
表1 C608来流和边界条件Table 1 Freestream and boundary conditions of C608
2.2 网格收敛性研究
声爆近场输入信号计算采用自研CFD软件[27-28],湍流模型为SA模型,近场距离为3个C608飞行器长度(z= 82.29 m)。网格使用SBPW-3提供的非结构混合网格[7],半模网格节点数约5 021万,特征网格尺度h定义为:
当此特征网格尺度h= 0.58时,网格具有较好的收敛性。具体网格细节见表2。

表2 非结构混合网格Table 2 Unstructured hybrid grid
远场地面波形计算利用自研声爆程序[15]。选取上述CFD计算所得到的近场过压值分布作为输入信号,利用增广Burgers方程计算远场地面波形。由于增广Burgers方程具有两个维度(时间维度和空间维度),在进行网格收敛性研究时需要依次对这两个维度展开分析。在均匀网格下,采用不同空间网格密度和时间网格密度,具体网格量见表3和表4。表中,NZ为空间网格点数,NT为时间网格点数。也可用时间采样率表示时间网格密度。
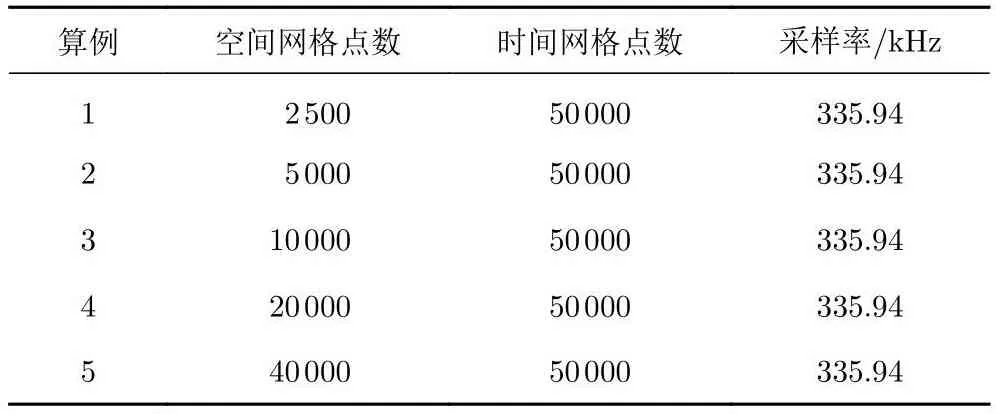
表3 不同空间网格密度Table 3 Different spatial grid sizes
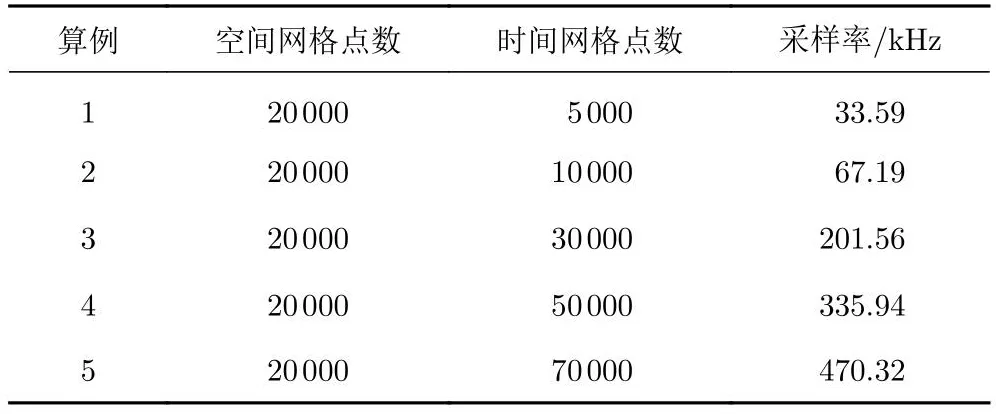
表4 不同时间网格密度Table 4 Different temporal grid sizes
图2和图3分别给了出远场地面波形在空间和时间维度上的网格收敛性。由图可见,地面波形对空间和时间网格密度都有一定敏感性,但需要加密到一定程度后,远场地面波形信号才能逐渐收敛。对于该算例,当空间网格密度和时间网格密度分别达到20 000点和30 000点以后,网格达到收敛,此后地面波形基本不随网格密度变化。
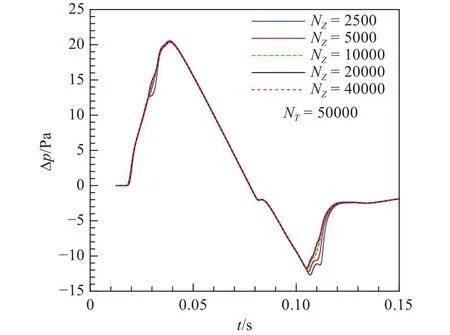
图2 不同空间网格密度收敛性Fig.2 Spatial grid convergence
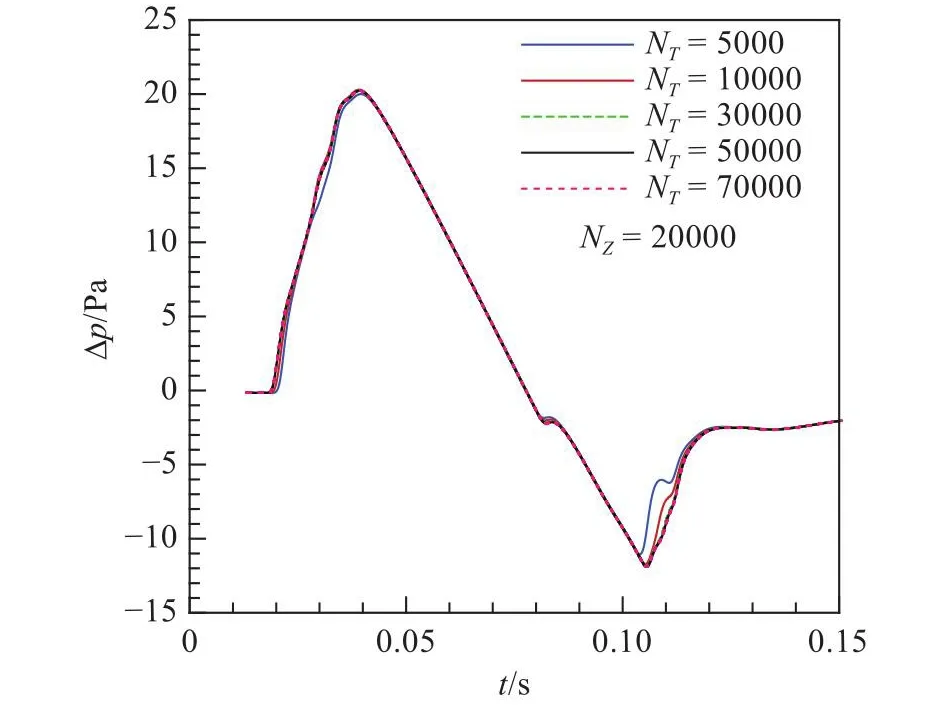
图3 不同时间网格密度收敛性Fig.3 Temporal grid convergence
综上所示,利用增广Burgers方程计算远场地面波形时,需适当加密网格。基于上述分析,本文选用网格NZ= 20 000和NT= 50 000开展研究。
3 基准状态分析
3.1 基准状态近/远场信号分析
几何模型为C608飞行器,三维外形见图1,基准状态飞行条件如表1所示。CFD计算采用SA湍流模型,空间格式为二阶精度,时间推进方法为GMRES 方法[29]。图4(a,b)给出了基准状态下马赫数和压力云图,图4(c)为飞行器表面压力分布图。机头产生激波和膨胀波对,在未受干扰前,细长的机身使流动平缓压缩。机翼前缘、舱盖后面的涡流发生器和ECS进气道产生了一系列快速变化的激波和膨胀波。入口溢出在机翼上形成一个高压区域。机翼后缘、水平尾翼、T型尾翼、发动机羽流等产生极其复杂的流动干扰,同时引发另一系列快速变化的激波和膨胀波。
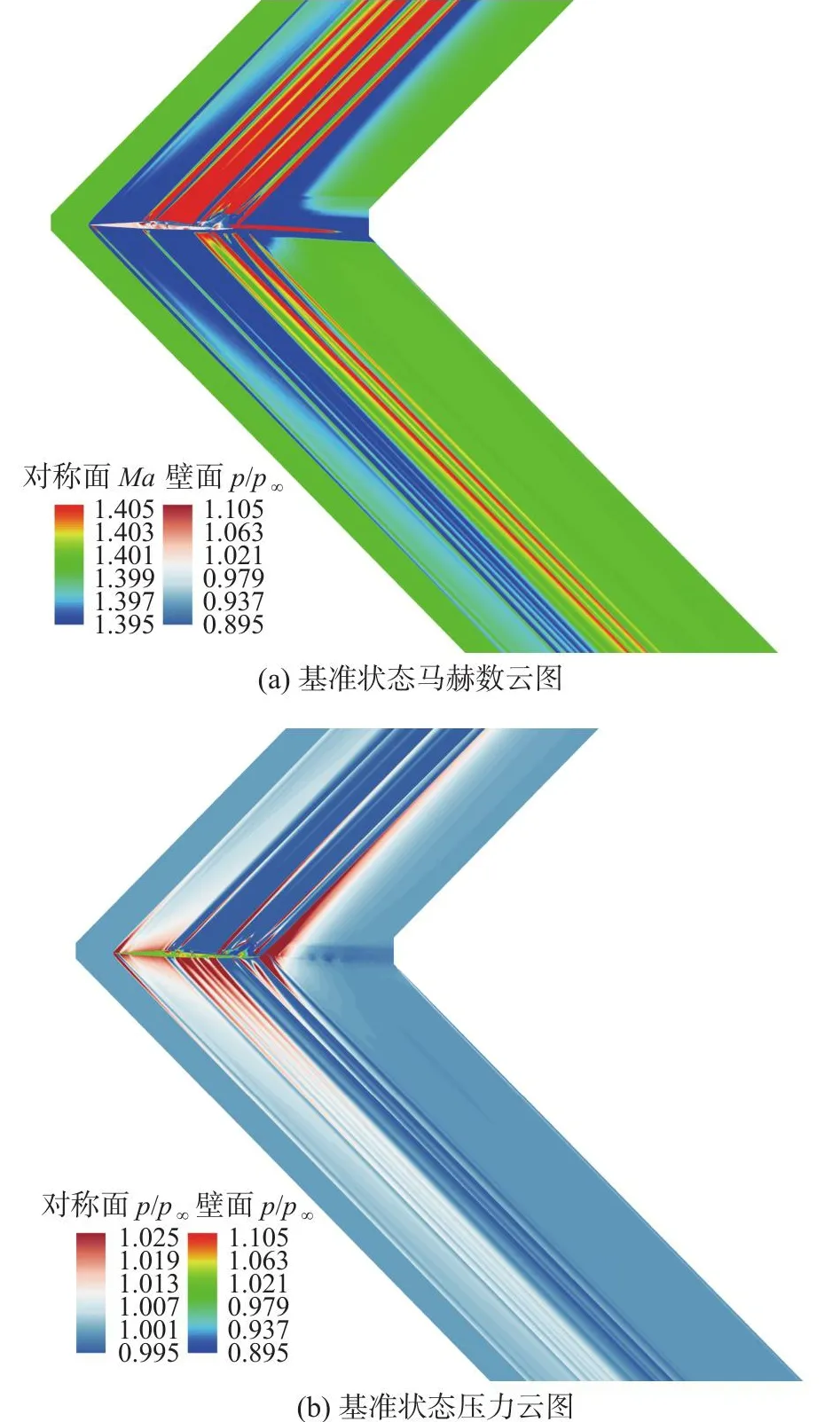
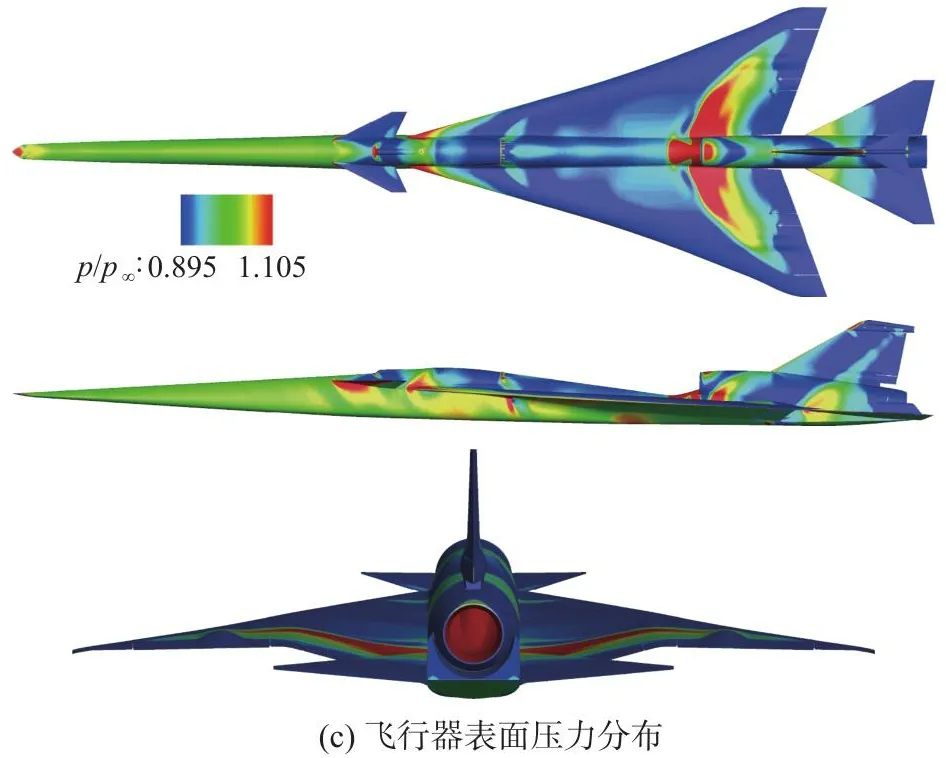
图4 飞行器基准状态云图Fig.4 Aircraft in the reference state
图5和图6分别对比了当前计算的近/远场波形与SBPW-3公布数据[8]的差异,其中红色和黑色线为SBPW-3数据,绿色实线为自研程序计算数据。可以发现,预测的近/远场波形与SBPW-3数据基本重合,说明自研CFD程序和声爆程序计算准确度符合要求,达到了较好的精度。整体近场过压值分布变化频率较高,存在多个波峰和波谷。由于经典吸收、分子弛豫效应等,使得大气具有类似低通滤波器的性质,声波能量及高频脉动在大气传播过程中被消耗成内能,因而远场地面波形较为平滑。
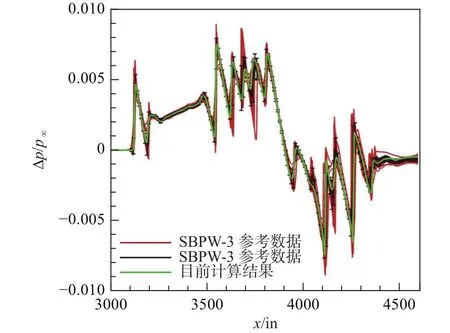
图5 近场过压值分布与SBPW-3数据对比Fig.5 Comparison of near-field over-pressure values with SBPW-3 data
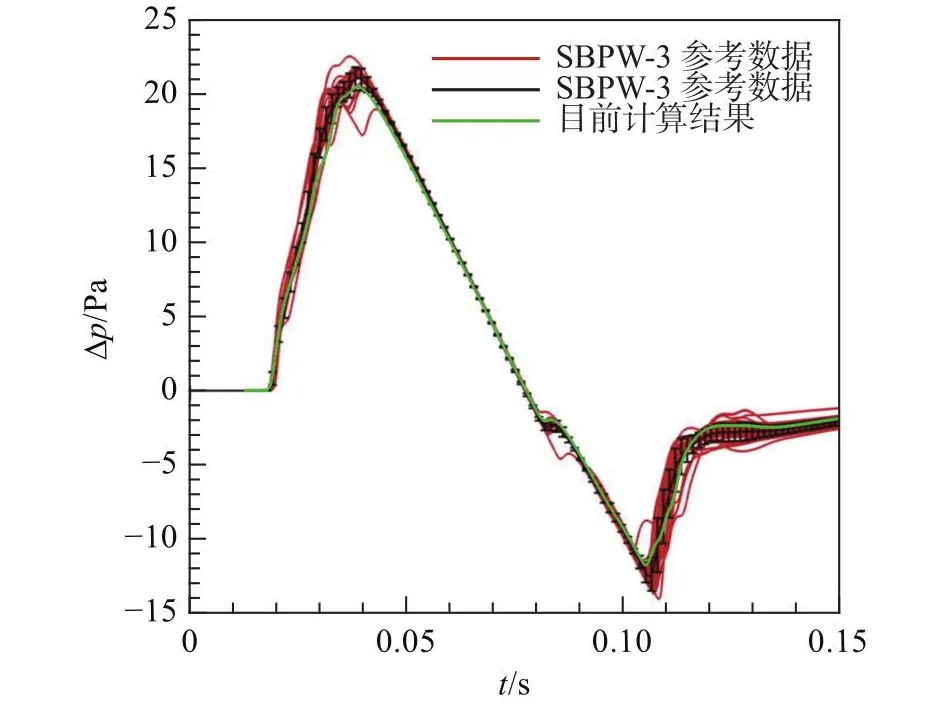
图6 远场地面波形与SBPW-3数据对比Fig.6 Comparison of far-field ground waveform with SBPW-3 data
3.2 物理模型影响
本文选取层流模型、SA模型、SA-QCR模型[30]和SST模型来研究物理模型对近场过压值分布及远场地面波形的影响。
首先,给出层流模型下计算所得的马赫数和压力云图(见图7)。与SA湍流模型(见图4)相比,层流模型马赫数和压力云图在上下部分和飞行器前部与SA模型计算结果类似,在飞行器尾流部分两者相差较大,其主要原因在于尾部区域喷流与主流之间有较强的剪切、湍流掺混,该区域用层流模型是不合适的。
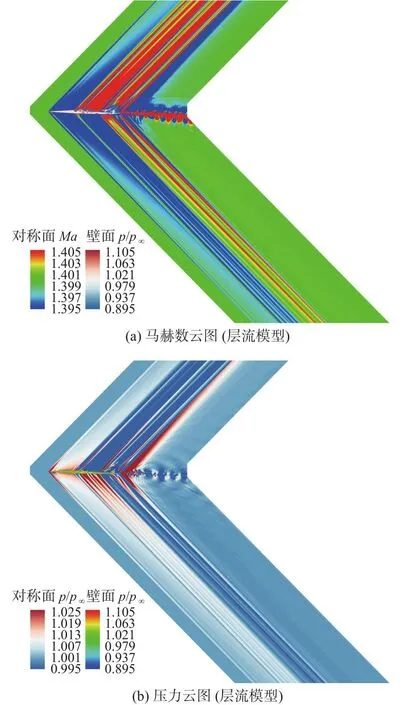
图7 层流模型下马赫数和压力分布Fig.7 Mach number and pressureobtained by a laminar model
接着,图8和图9对比了不同物理模型下近场过压值分布和远场地面波形的差异。从图中可以看出:层流模型与湍流模型计算结果差别较明显(尤其尾部区域),同时层流模型对地面波形过压值预测偏低;SA湍流模型与SA-QCR湍流模型计算结果几乎重合;SST湍流模型与SA湍流模型,前部波形几乎一致,只有在尾部区域有较明显的差异。综合来看,不同湍流模型对近/远场波形的影响相对较小,层湍模型对近/远场波形的影响相对较大。
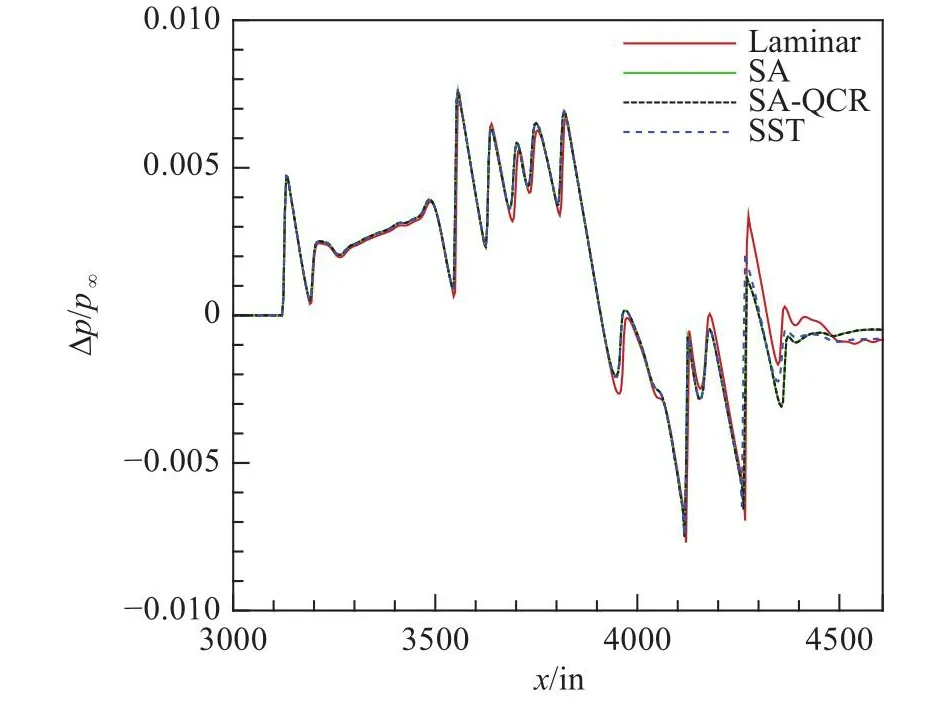
图8 不同物理模型下近场过压值分布Fig.8 Distributions of near-field over-pressure values obtained by different physical models
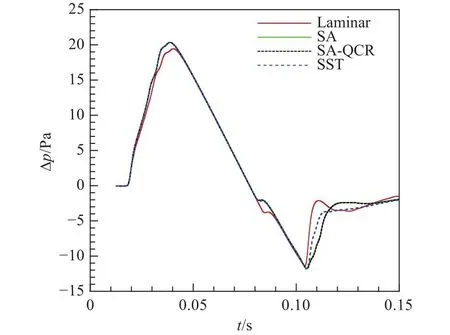
图9 不同物理模型下远场地面波形Fig.9 Far-field ground waveforms obtained bydifferent physical models
3.3 相对湿度影响
未来超声速客机飞行将跨越海洋和大陆,两者之间的相对湿度相差较大,而分子弛豫效应的强度与空气湿度极为相关,因此本节研究不同湿度对地面波形的影响。
简单起见,考虑5个不同的相对湿度(10%、30%、50%、70%、90%)进行计算,其中10%相对湿度近似模拟沙漠等干旱地区湿度,90%相对湿度近似模拟沿海等湿润地区湿度。图10给出了在不同相对湿度的大气中的远场地面波形。可见,相对于高湿度,低湿度对波形幅值的影响较大。相对湿度越低的大气,其远场地面波形的过压值峰值更低,这是由于干燥的空气对于声波的耗散更强。文献[31]表明,对于声波在大气中的传播过程,因分子弛豫效应而产生的衰减,可以用一个衰减因子来衡量衰减的快慢,而声爆波形频率分量大多处于约化声波频率较低处,约化衰减因子会随相对湿度的减小而增大,因此干燥的空气对声爆波形的耗散作用更强。此外需要说明的是,除本小节外,本文其余计算均假定相对湿度为70%。
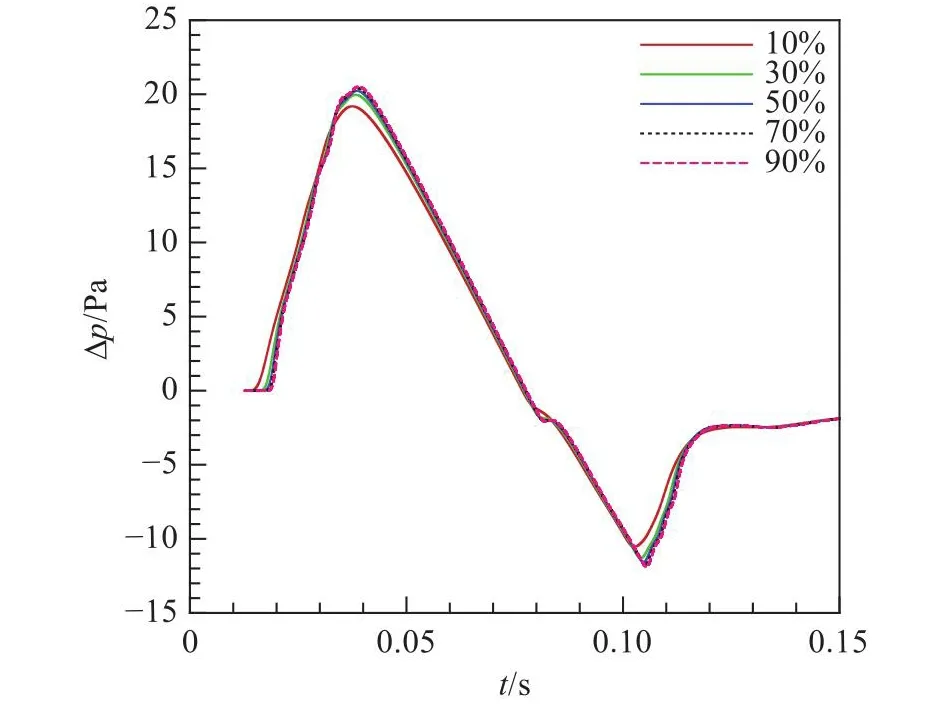
图10 不同相对湿度下远场地面波形Fig.10 Far-field ground waveforms under different relative humidity
4 不确定度量化分析
超声速客机在高空飞行过程中,来流条件会不断发生波动。因此需要考虑来流参数存在不确定性时对声爆预测结果的影响,并甄别来流参数中影响声爆预测的关键性因素,为超声速客机工程实际应用提供有价值的参考。本文选用C608低声爆超声速飞行器为研究对象,采用SA湍流模型和增广Burgers方程开展声爆近/远场信号不确定度量化分析。
4.1 样本点选取
超声速客机巡航飞行环境一般位于大气平流层,平流层中来流温度基本不变。本文选取三个来流参数变量(来流马赫数、来流攻角和单位雷诺数)作为随机不确定性输入参数,同时将地面波形过压值Δp作为输出响应,开展声爆近/远场波形的不确定传播和参数敏感性分析。三个变量的取值范围参考SBPW-3官网[7]和相关文献[8,17],并假设均服从均匀分布,不确定范围设置如表5所示。其中:来流马赫数基准值1.4,变化范围为±3%,对应参数变化范围为[1.358, 1.442];来流攻角基准值0°,参数变化范围为[-0.2°, 0.2°];单位雷诺数 4 321 890 m-1,变化范围±10%,对应参数变化范围为[3 889 701 m-1, 4 754 079 m-1]。
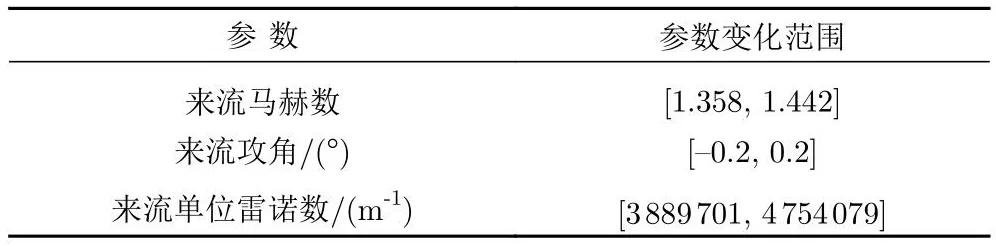
表5 输入变量参数变化范围Table 5 Ranges of input variables
点配置非嵌入式多项式混沌方法(NIPC)采用二阶截断,为了更高精度地计算混沌多项式的系数,采用两倍过采样样本。因此,本文利用拉丁超立方抽样方法抽取20个样本点。如图11所示,本文选取的样本点分布均匀。在每一个选取的样本点上开展确定性的近场CFD计算和远场增广Burgers方程计算。后续将根据样本点上的计算结果开展声爆近/远场信号不确定性量化分析。
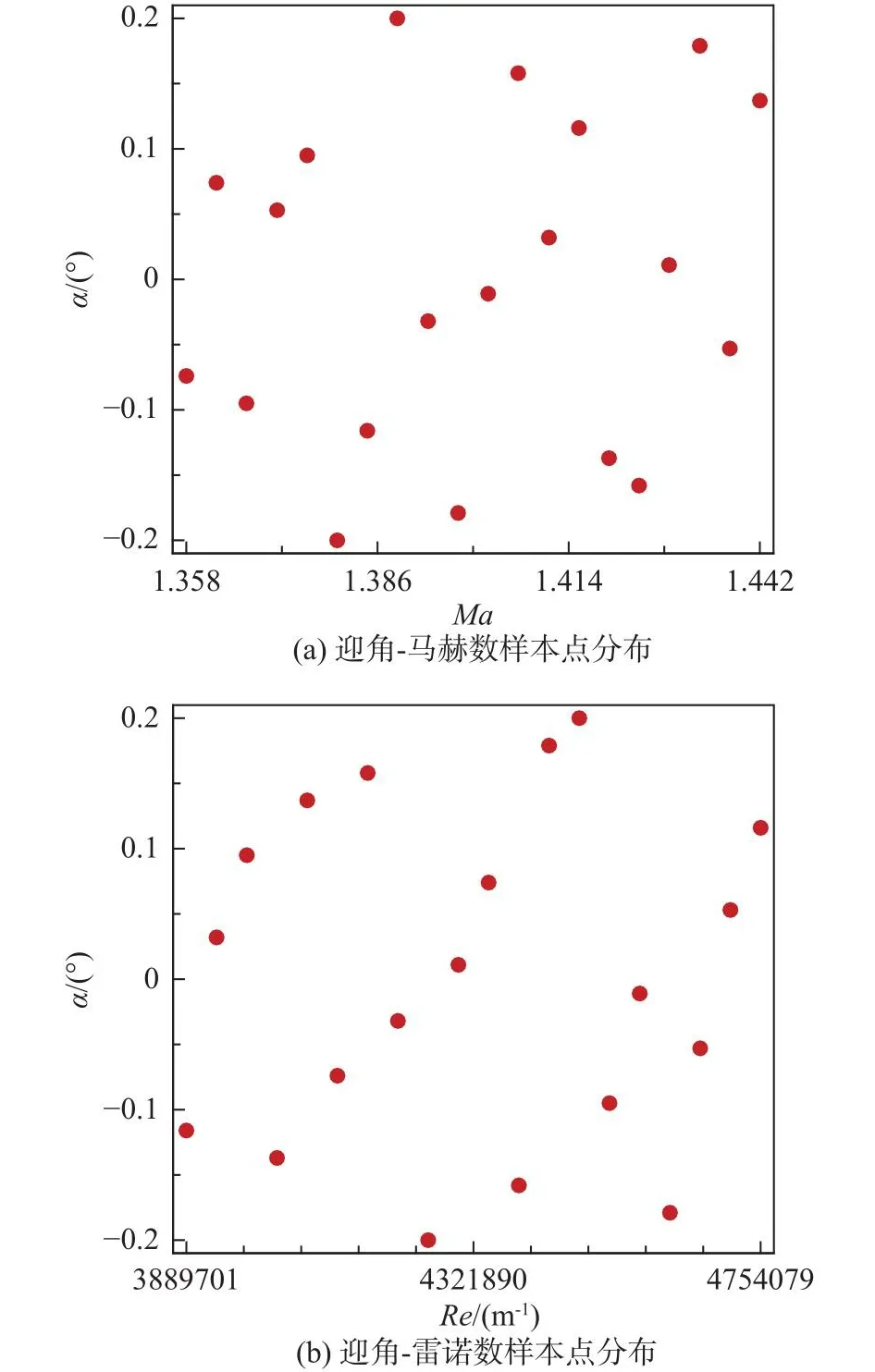
图11 拉丁超立方抽样方法抽取样本点Fig.11 Latin hypercube design method for sampling points
4.2 近场波形不确定度量化分析
为了便于开展不确定度量化分析,将所有样本近场波形第一个波峰起点取为一致。图12给出所有样本点近场过压值分布。从中可以发现,在近场过压值的波峰、波谷等处存在较大的不确定度。
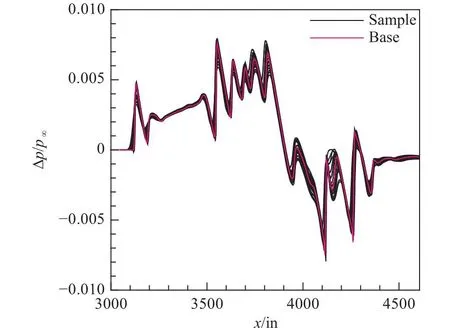
图12 所有样本点近场过压值分布Fig.12 Near-field over-pressure values at all sampling points
在95%置信区间内,声爆信号的不确定区间为(µ-1.96σ,µ+1.96σ),区间大小为 2 ×1.96σ,其中 µ为平均值,σ为标准差。图13为NIPC方法计算的近场过压值均值与基准状态近场过压值。从图中可以看到,基准状态下的近场过压值和NIPC近场过压值均值基本一致,在波峰、波谷处有一定差异。
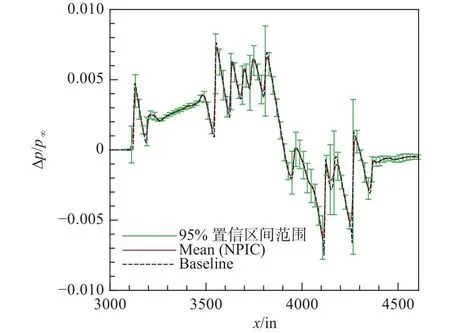
图13 近场过压值均值Fig.13 Mean value of near-field over-pressure
4.3 远场波形不确定度量化分析
本文将所有样本远场地面波形起点取为一致,以便开展不确定度量化分析。图14给出所有样本点远场地面波形分布。可以发现,整体地面波形在第一波峰、中间转折及波谷处存在较大的不确定度。
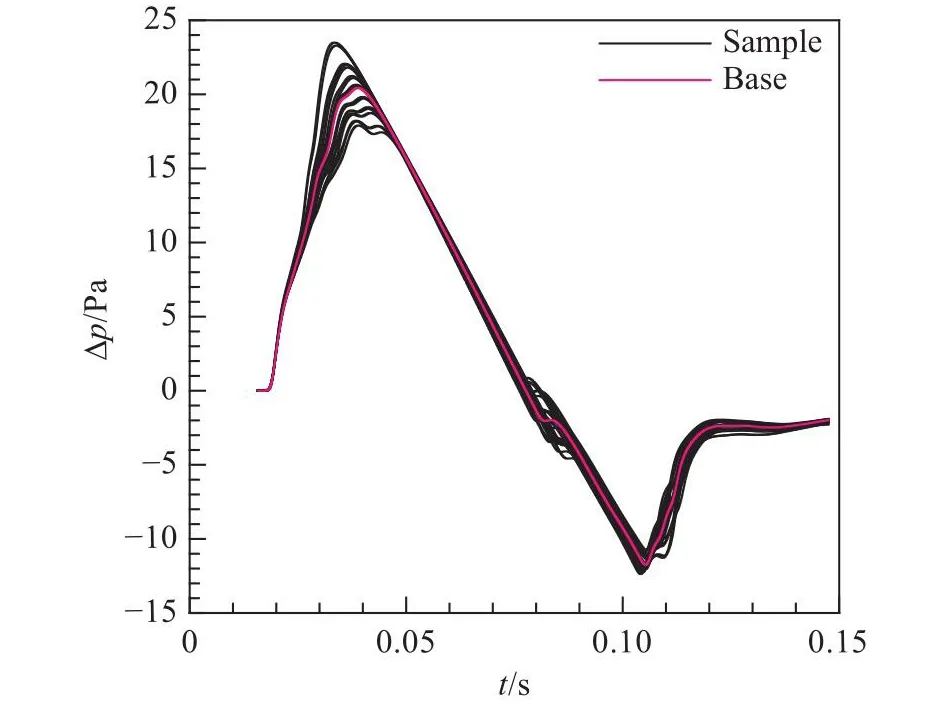
图14 所有样本远场地面波形分布Fig.14 Far-field ground waveform distributions of all samples
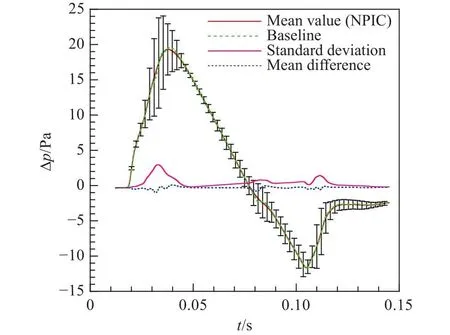
图15 地面波形均值和标准差Fig.15 Mean and standard deviation of ground waveforms
图16分别给出了不同来流参数的敏感性(Sobol)指数分布。通过前述三个来流参数不同时刻对应的敏感性指数分析,可以观察到来流参数对声爆传播的影响程度。由图16可知,来流单位雷诺数对地面波形过压值的影响显著低于来流马赫数和来流攻角的影响,后两者对地面波形不确定度贡献较大。从流动机理上来看,声爆近场及远场过压分布取决于脱体膨胀波和压缩波,其中来流马赫数和迎角对脱体空间波系结构特征影响较大,而雷诺数主要作用于物面附近,对脱体空间波系结构特征影响相对较小。
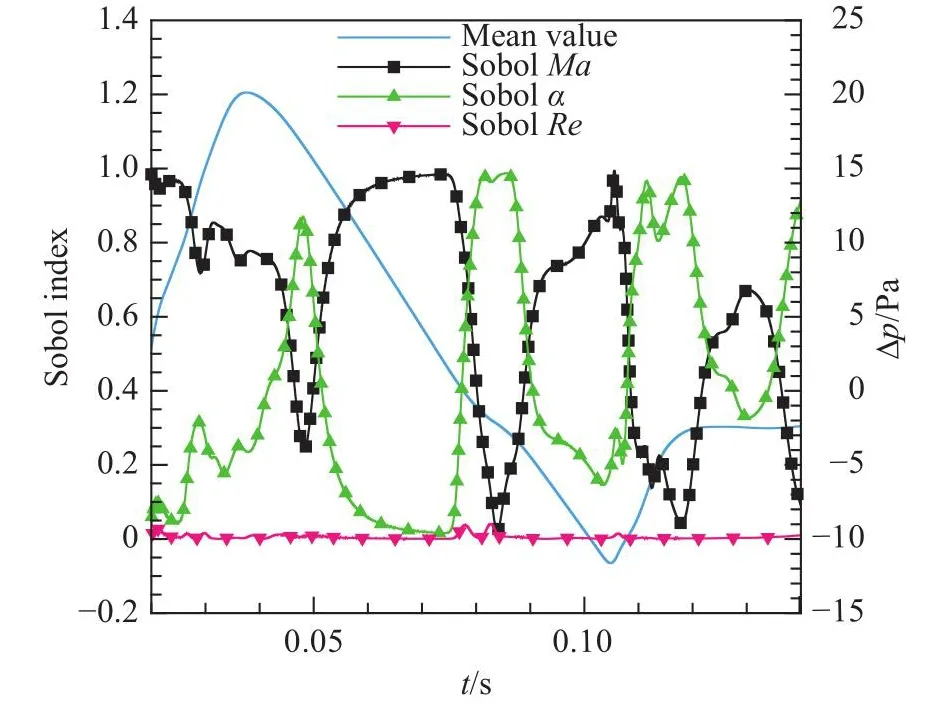
图16 地面波形敏感性指数Fig.16 Sobol index of ground waveform
不确定度量化和敏感性分析表明,在低声爆超声速飞行器声爆传播预测数值模拟中,需要重点关注来流马赫数和来流攻角的变化。不确定性输入变量会引起远场地面波形、波峰与波谷处的过压值产生明显变化。来流马赫数变化(±3%)和来流攻角变化([-0.2°, 0.2°])对地面波形 Sobol指数贡献最大的分别是t= 0.074 14和t= 0.085 84时刻,对应Sobol指数分别为0.984 4和0.986 8。
5 结 论
本文对AIAA第三届声爆预测研讨会提供的C608低声爆超声速飞行器开展了声爆传播预测及不确定度量化分析,开展了远场地面信号空间维度和时间维度上的网格收敛性研究,并对比基准状态下不同湍流模型以及相对湿度对声爆预测的影响。此外,选取来流马赫数、来流攻角及来流单位雷诺数等三个不确定性输入变量,采用非嵌入式多项式混沌方法对声爆近/远场信号进行了不确定度量化分析和敏感性分析,得到的结论如下:
1) C608飞行器标准算例声爆近/远场波形与SBPW-3公布数据相吻合,表明自研CFD软件及声爆程序计算准确度符合要求,具有较好预测精度。
2) 层流模型相较于湍流模型,在飞行器尾流部分预测较差,同时对地面波形过压值预测偏低,不同湍流模型之间对声爆近/远场波形的影响较小。当相对湿度大于30%时,相对湿度对声爆近/远场波形的影响基本可以忽略不计。
3) 采用基于非嵌入式多项式混沌方法的不确定度量化分析方法,得到了近场波形均值、远场波形均值和标准差等。其中近/远场波形过压值均值与基准状态均值基本一致,仅在波峰和波谷处有一定差异。
4) 采用基于Sobol指数的敏感性方法,对地面波形过压值 Δp进行了敏感性分析。其中来流单位雷诺数对地面波形过压值的影响显著低于来流马赫数和来流攻角的影响。此外,声爆地面感觉噪声级是对不同频率噪声强度的量化,与远场过压分布之间呈非线性关系,今后应开展基于感觉噪声级的不确定度分析。
5) 来流条件的波动影响声爆近/远场信号,其中气流变化频率或飞行器运动频率对声爆信号传播产生复杂影响,如超声速加速飞行发生声爆聚集现象[32],有待开展深入研究。

