一类新型自适应反扩散近似Riemann求解器及其应用

刘旭亮，范召林，张树海1，，李 虎1，，罗 勇1，，孙晓峰

(1.中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000；2.中国空气动力研究与发展中心，绵阳 621000；3.北京航空航天大学 能源与动力工程学院，北京 100191)

0 引 言

双曲守恒律方程的空间离散需要构造数值通量，而数值通量的构造方法主要分为两大类：一类方法是通量分裂，包括Lax-Friedrichs分裂[1]、Steger-Warming分裂[2]和Van Leer分裂[3]等；另一类方法是Riemann求解器，或称为Riemann算子。

Riemann求解器是数值求解双曲系统的重要组成部分。对于守恒形式的双曲系统，已有许多学者提出了多种著名的Riemann求解器。精确的Riemann求解器由Godunov[4]在1959年提出，具有耗散小、精度高等优点，但计算量过大。后续学者发展出了多种近似Riemann求解器并对其进行改良。1981年，Roe[5]提出了著名的近似Riemann求解器，该求解器是对非线性Euler方程组的特殊线化。但是原始Roe算子的主要缺陷是在特定问题中违反熵增条件，因此Roe算子必须进行熵修正才能保证计算的准确性。1983年，Harten等[6]提出了HLL型Riemann求解器，HLL算子非常高效且有很好的鲁棒性，满足熵增条件，并保持正定性，但HLL算子耗散较大且不能完全解决接触间断的问题。在HLL算子的基础上，Einfeldt等[7-8]提出了HLLEM型近似Riemann求解器，这类求解器具有正定保持性质并且是熵增的。Einfeldt等[8]通过构造反扩散系数来降低HLL算子的耗散，并证明了HLLEM求解器和Roe求解器的区别仅在于数值信号速度的不同，因此，HLLEM求解器依然可能在计算激波时出现不稳定。为了克服HLL算子无法模拟接触间断的缺陷，Toro等[9]提出了HLLC型Riemann求解器，恢复了HLL算子中丢失的接触波和剪切波。HLLC算子保留了HLL算子的熵增特性和正定保持性质，但在计算激波中仍然会出现非物理的数值振荡。基于由相空间中的路径积分来得到数值耗散项的构造思路， Osher等[10]提出了Osher型Riemann求解器，其优点是数值通量光滑并且满足熵增特性。在具体计算时，HLLEM求解器与Roe求解器仅需求解特征值和相关的左右特征向量，而Osher型Riemann求解器需要计算整套的特征系统，因此Osher求解器计算量较大。为了将通量中的线性项和非线性项加以区别，Liou[11]等提出了一种结合通量分裂和Riemann求解器的AUSM系列格式，这种方法把压力项和对流项进行分裂，对部分问题能够消除计算激波的不稳定性现象。

通过与激波捕捉格式结合，近似Riemann求解器广泛应用于超声速流动的数值模拟。但是，在高维计算中，使用近似Riemann求解器可能会遇到激波计算的不稳定性问题。1988年，Peery和Imlay[12]首先报道了计算激波不稳定的红玉现象（carbuncle phenomenon），他们使用Roe的近似Riemann求解器计算了钝头体周围的超声速流场，发现Riemann求解器的数值不稳定性可能会严重影响激波计算的准确性。从那时起，许多学者开始研究和解决红玉现象问题。防止Riemann算子计算激波时出现不稳定性，主要有三类方法：第一类是Harten熵修正方法[13]，该方法是对Riemann算子的特征值在接近零时强制增大。熵修正方法引入了自由参数，在实际应用中自由参数设置过大或者过小时都可能导致计算崩溃，并且不同的问题要选取不同的自由参数，因此熵修正方法的经验性非常强。第二类是Quirk提出的混合方法[14]。Quirk注意到，某些耗散小的Riemann求解器总是出现红玉现象，而其他耗散较大的Riemann求解器则没有这种不稳定性。Quirk建议在激波区域使用耗散大的Riemann求解器，而在其他区域使用耗散较小的Riemann求解器，基于此类混合方法来计算激波问题可以克服数值不稳定现象。尽管具体的组合方式可能有着显著差异[15-17]，但类似的思路已经被广泛采用。第三类是构造高维Riemann求解器方法。由于在高维问题中计算激波更容易出现不稳定性问题，一些研究者发展了高维近似Riemann求解器[18-19]或旋转Riemann求解器[20-21]。此类方法本质上是高维的，可以部分抑制激波不稳定性。根据Huang等[16]的研究，在实际计算中使用混合方法的计算效率高于旋转Riemann求解器，他们认为混合方法更高效，同时也具有较好的鲁棒性。目前在求解高维双曲守恒律方程时，更常用的策略是采用局部一维Riemann求解器来计算数值通量，高维Riemann求解器方法应用还不够广泛。

混合方法能够解决激波计算不稳定性问题，同时也能避免熵修正方法中自由参数的经验性，因此混合方法在实际计算中比较常用，但必须选择适当的基础Riemann求解器和混合因子。近年来，Dumbser等[22]和Xie等[23]基于HLLEM算子的反扩散矩阵来构造混合Riemann求解器，他们认为以HLLEM算子作为基础，对接触波和剪切波分量进行修正的混合方法比较合理。

为了消除近似Riemann求解器在数值模拟激波时出现的计算不稳定性现象，本文采用混合方法对反扩散矩阵进行修正，发展了一类新型具有自适应反扩散的近似Riemann求解器。该求解器应用到高阶格式时，能够保持差分格式的高阶精度，并且计算稳定性较好。

1 数值格式的构造

1.1 控制方程和差分格式

本文的数值方法主要应用于双曲守恒率方程。以二维可压缩Euler方程为例：

其中，守恒变量为：

x、y方向的通量分别为：

本文的数值方法主要是离散Euler方程的对流项，下面以 ∂F/∂x的离散为例进行说明。

选取图1的网格模板，网格结点处的一阶导数由线性中心紧致格式[24]来得到。

图1 紧致格式的模板Fig.1 Stencil for compact scheme

为了能够计算包含激波等复杂流动的非线性问题，紧致格式（4）中可以采用Riemann求解器来近似。通过半结点处的通量把迎风和耗散性引入到差分格式，下标L表示半结点左侧方向，R表示半结点右侧方向。其中半结点处的值和由混合加权非线性插值[25]得到。因为的系数关于与是对称的，所以只需给出的构造方法。

其中非线性权为：

其中线性权为：

光滑因子的详细公式参考文献[25]。优化参数的选择为：α=0.25， σ =0.67。

本文记这类格式为混合优化非线性紧致格式（hybrid optimized nonlinear compact scheme, HONCS），本文主要采用五阶混合优化非线性紧致格式，简单记为HONCS5。

1.2 数值信号速度

由于数值信号速度在Riemann求解器的计算中起着影响耗散性的重要作用，同时构造所有的Riemann求解器都要先指定数值信号速度。因此在说明Riemann求解器之前，先给出几种常用的数值信号速度。

1.2.1 Roe类型[5]

1.2.2 Einfeldt 1988类型[7]

1.2.3 Einfeldt 1991类型[8]

1.2.4 Batten类型[26]

1.2.5 Davis类型[27]

1.2.6 Toro类型[28]

其中K=L或者K=R。

数值信号速度为：SL=qL-ηLcL，SR=qR+ηRcR。

1.3 传统Riemann求解器

为了行文方便，选取如下符号：S-=min(SL,0)和S+=max(SR,0)。

定义左右状态通量之差为：

则有如下关系式：

1.3.1 Roe 型Riemann求解器[5]

特征值为：

原始Roe算子可以表示成如下几种形式：

直接采用原始Roe算子求解激波问题，通常会出现熵违反解[28]，必须对特征值进行熵修正才能得到正确解。但是一般来说，熵修正的经验性很强，并且特定问题必须采用特定的熵修正值，因此目前还没有标准的做法。

1.3.2 HLL型Riemann求解器[6]

HLL通量用S-、S+可以表达为：

把关系式（9）代入式（15），则可简洁地表达为：

1.3.3 HLLC型Riemann求解器[9,28]

中间星区守恒变量为：

其中：

1.3.4 HLLEM型Riemann求解器[8]

以二维问题为例，HLLEM通量[8]为：

把关系式（9）代入式（21），则可表示为：

其中：

反扩散系数的定义为：

1.3.5 通量分裂型Riemann求解器

一些学者[29-31]采用通量分裂的方式来构造Riemann算子，即通过来计算数值通量。但是Steger-Warming分裂[2]、Van Leer分裂[3]等是逐点分裂的，无法表示成Riemann算子的通用形式。只有局部Lax-Friedrichs分裂可以变换成通用形式其中局部分裂系数为表示局部分裂点坐标。通量分裂型Riemann算子不是本文关注的重点，因此不做详细比较和讨论。

1.4 新型自适应耗散RAD型Riemann求解器

由于HLLEM算子和原始Roe算子在数值信号速度相同时完全等价[8]，所以HLLEM算子中的反扩散系数在激波附近取值较大，导致在计算激波时出现不稳定现象。

为了能够保持HLLEM算子在光滑区的低耗散特性，同时能够稳定地计算激波，本文构造了新型混合反扩散矩阵，以二维问题为例：

其中， φi∈ [0,1]是自适应混合因子：

流场光滑量度为：

本文中取无量纲参数 ε =1×10-40。本文中若无特殊说明，则无量纲参数 δ =1×10-4。

显然，矩阵D的特征值可以写成：

当S+=SR＞0且S-=SL＜0时，即流动是亚声速时，令则可以得到反扩散矩阵

通过对比RAD求解器与Roe、HLL和HLLEM等Riemann求解器的公式，可以得到如下的等价关系：

因此，传统的Roe、HLL、HLLEM等Riemann求解器都是本文新型RAD求解器的特殊形式。

根据自适应混合因子的定义，当流场处于光滑区时， φi≈ 1，即当流场处于间断区时，所以，新型RAD求解器在光滑区耗散较小，而在间断区能够抑制激波计算的不稳定性。

2 格式精度验证和频谱分析

2.1 数值信号速度的选择

为了确定在Riemann算子中的数值信号速度，本文采用修正Sod激波管问题[26,28]来验证和比较计算结果。该问题包含激波、膨胀波、接触间断等，能够很好的评估数值方法的熵满足特性。计算网格采用100个点，计算到无量纲时间t= 0.2，间断左右两边参数为：

图2给出了基于一阶迎风格式和HLLEM算子的不同数值信号速度的计算结果，可以看出，Roe类型、Einfeldt 1988类型和Einfeldt 1991类型的信号速度的计算结果明显有振荡。Toro类型的信号速度比较复杂，不易从数学上证明正定保持特性[26]。Davis类型信号速度耗散比Batten类型的大。因此，本文全部采用Batten类型数值信号速度。

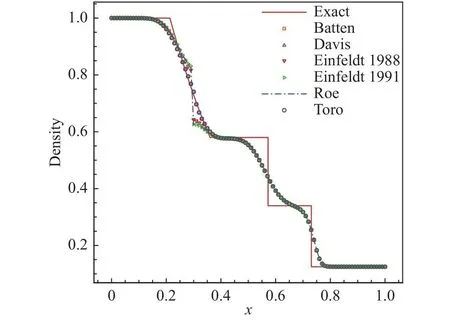
图2 数值信号速度的比较Fig.2 Comparison of numerical signal velocities

2.2 精度验证

为了验证数值方法的精度，选取如下的格式：时间离散采用三阶TVD Runge-Kutta格式[32]，空间离散采用五阶HONCS差分格式，数值通量计算采用RAD型Riemann求解器。

以一维Euler方程的对流密度波问题为验证标准[33]，其精确解为： ( ρ,u,p)=(1+0.1sin[π(x-t)],1,1)。计算域取 [0 ,2]，边界取周期性边界条件，计算的最终时刻为t=20，初始计算网格为15个点，CFL= 0.5。随着网格点数增多，CFL数为CFL2=CFL1(N2/N1)3-n/3。其中：下标“1”表示上一个时间层的值；下标“2”表示下一个时间层的值；N表示网格点数；n表示空间离散精度。计算得到的数值结果如表1所示。结果表明五阶HONCS格式达到了设计精度，验证了RAD型Riemann求解器能够应用于高阶精度格式。

表1 五阶HONCS格式的数值精度验证Table 1 Numerical orders of accuracy for HONCS5 scheme

2.3 频谱分析

本文采用Pirozzoli[34]的ADR（approximate dispersion relation）方法来分析五阶HONCS格式的分辨率和耗散。该方法现在被广泛地应用于非线性激波捕捉格式的频谱分析[35-36]。计算得到的修正波数实部对应于格式的色散（分辨率），而虚部对应于格式的耗散。

为了更清楚地说明五阶HONCS格式的频谱特性，对比了经典五阶WENO格式[37]。从图3、图4中可以看出，五阶HONCS格式的分辨率高于五阶WENO格式的分辨率，并且五阶HONCS格式的耗散远小于五阶WENO格式。

图3 数值格式的色散特性Fig.3 Dispersion of numerical schemes

图4 数值格式的耗散特性Fig.4 Dissipation of numerical schemes

3 数值实验与分析

空间离散采用五阶HONCS格式结合各类Riemann求解器，时间离散采用三阶TVD Runge-Kutta格式，计算了Titarev-Toro问题、激波衍射问题、激波双马赫反射问题、钝头体绕流问题算例。对于二维问题，也给出了一阶迎风格式的计算结果，其目的是为了更清晰地对比Riemann求解器计算激波的稳定性。需要说明的是，Einfeldt等[8]证明了HLLEM求解器和Roe求解器的区别仅仅在于数值信号速度的不同。在本文的数值算例中，所有Riemann求解器采用的数值信号速度是相同的，因此HLLEM求解器和Roe求解器是等价的，本文只给出HLLEM求解器的计算结果。

3.1 Titarev-Toro问题[38]

该问题流场中含有丰富的密度波结构，能够考察计算格式对流场细节的分辨能力，是验证数值格式的标准算例。该问题的初始条件为：

计算区域取为[-5, 5]，计算网格采用1 000个点，初始间断位于x=-4.5处，最终计算时刻取t= 5。

采用五阶HONCS格式结合四种不同的Riemann求解器进行计算，密度波的分布如图5所示。从计算结果可以看出，新型RAD算子与HLLC算子和HLLEM算子的表现十分接近，这是因为本问题的密度波不是间断的，流场比较光滑，使得RAD算子的效果接近于HLLEM算子，从而说明RAD算子的混合因子取值是合理的。HLL算子因为耗散比较大，在本问题中对高频密度波的分辨率结果相对较差。

图5 HONCS5格式求解Titarev-Toro问题Fig.5 Solutions of the Titarev-Toro problem obtained by HONCS5 scheme

3.2 激波衍射问题[14]

激波衍射是由Quirk[14]提出的膨胀波问题，被广泛用来验证Riemann求解器计算激波的稳定性[21，23]。该问题描述的是马赫数5.09的激波从90°拐角的台阶角点处运动，激波沿x方向从左向右传播，计算区域取[0, 1]× [0, 1]。激波波前静止空气的密度为1.4，压力为1，波后按运动激波关系给定初始条件。初始物理参数为：

左边界在[0, 0.5]的区域给定反射壁面边界条件，在(0.5, 1]的区域给定波后值。上边界区域根据激波运动所在的位置给定波前值或波后值。下边界和右边界给定波前值。本文采用800 × 800的均匀网格，计算终止时刻为t= 0.18。

图6和图7分别给出了一阶迎风格式和五阶HONCS格式的计算结果，取密度为0.5～7.3共30条等值线作图。

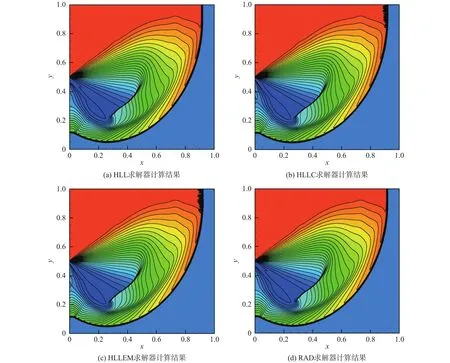
图6 一阶迎风格式求解激波衍射问题Fig.6 Numerical results of the shock diffraction problem obtained by first-order upwind scheme

图7 HONCS5格式求解激波衍射问题Fig.7 Numerical results of the shock diffraction problem obtained by HONCS5 scheme

因为强激波附近是间断区域，根据混合因子的定义可知，新型RAD算子在激波附近的计算效果接近于HLL算子。从计算结果可以看出，新型RAD算子和HLL算子都能够准确地计算运动激波、膨胀波和再生二次激波。

对于一阶迎风格式，从图6中可以看出，采用HLLC算子和HLLEM算子会导致计算正激波出现红玉现象。对于五阶HONCS格式，从图7中可以看出，采用HLLC算子会出现严重的红玉现象。而采用HLLEM算子会出现负密度，导致计算发散，无法得到最终解。从图6和图7的对比中还可以发现，高阶五阶HONCS格式对于接触面的分辨率明显优于迎风格式。

3.3 激波双马赫反射问题[39]

双马赫反射问题包含强激波和滑移线，非常适合于考察格式的激波捕捉能力和流场精细结构的分辨率。本问题描述的是马赫数为10的强运动斜激波以与x轴方向呈60°角的方向入射，入射点在（1/6, 0），计算区域取[0, 4]× [0, 1]。激波波前静止空气的密度为1.4，压力为1，波后按激波关系给定初始条件。初始物理参数为：

下边界在[1/6, 4]的区域给定壁面反射边界条件，其他边界按照激波运动所在的位置分别给定波前或波后的值。采用1 920×480的均匀网格计算到无量纲时间t= 0.2。

图8和图9分别给出了一阶迎风格式和五阶HONCS格式的计算结果，取密度为1.731～20.92共30条等值线作图。从计算结果可以看出，对于一阶迎风格式和五阶HONCS格式，新型RAD算子和HLL算子都能够准确地计算激波的马赫杆。对于一阶迎风格式，采用HLLC算子和HLLEM算子都会导致弯曲马赫杆现象[14]，HLLEM算子的计算结果比HLLC算子更不稳定。对于五阶HONCS格式，从图9中可以看出，采用HLLC算子在马赫杆处会出现红玉现象，而采用HLLEM算子会导致计算发散。从图8和图9的对比中还可以发现，高阶五阶HONCS格式对于滑移线的分辨率明显优于迎风格式。

图8 一阶迎风格式求解双马赫反射问题Fig.8 Numerical results of double Mach reflection problem for first-order upwind scheme

图9 HONCS5格式求解双马赫反射问题Fig.9 Numerical results of the double Mach reflection problem obtained by HONCS5 scheme

滑移线附近是相对光滑的区域，根据混合因子的机制可知，新型RAD算子在滑移线附近耗散应当低于HLL算子。图9的计算结果验证了新型RAD算子比HLL算子在滑移线附近的分辨率高。

3.4 钝头体绕流问题

超声速钝头体绕流问题是检验数值格式是否会遭遇红玉现象的典型算例。该问题的红玉现象通常是指钝头体绕流的弓形激波在驻点线附近发生异常的凸起。平头钝头体高度为0.4，长度为3.4，前缘位置x= 0.6，中心线位置y= 0。计算域为 [0, 4]× [-1, 1]。初始条件为马赫数3的强运动激波沿着x方向向右传播。流场初始物理参数为：

左边界取来流条件，上下边界和右边界为出流边界条件，钝头体壁面采用滑移壁面边界条件。采用800 × 200的均匀网格计算截止到无量纲时间t= 5的时刻。

图10和图11分别给出了一阶迎风格式和五阶HONCS格式的计算结果，取马赫数0.2～3.7共30条等值线作图。

图11 HONCS5格式求解钝头体绕流问题Fig.11 Flow fields around a blunt body obtained by HONCS5 scheme

钝头体绕流的强激波计算需要鲁棒的数值方法来克服数值振荡，由于五阶HONCS格式的耗散较小，需要耗散较大的Riemann算子来保证计算方法的稳定性。对于本问题，新型RAD算子参数调整为δ=1×10-10。

从计算结果可以看出，对于一阶迎风格式和五阶HONCS格式，新型RAD算子和HLL算子都能够准确地捕捉弓形激波，没有任何的非物理振荡现象。从图10中可以发现，对于一阶迎风格式，采用HLLC算子和HLLEM算子都会导致红玉现象，即沿着驻点线附近出现了明显的异常凸起结构，并且HLLEM算子比HLLC算子的红玉现象更严重。对于五阶HONCS格式，采用HLLC算子在弓形激波处出现红玉现象，而采用HLLEM算子会导致计算发散。

4 结 论

针对近似Riemann求解器在计算激波时的数值不稳定性问题，通过合理设计反扩散矩阵，发展出一类新型RAD近似Riemann求解器。

通过适当的变换，可以发现传统的Roe、HLL、HLLEM等Riemann求解器都是RAD求解器的某种特殊形式。本文构造了自适应混合因子，得到的新型RAD算子能够抑制HLLEM算子和HLLC算子出现的计算激波不稳定现象。根据混合因子的机制，新型RAD算子比HLL算子在滑移线等光滑区域的耗散小。

新型RAD求解器不但能够应用于低阶迎风格式，并且能够广泛应用到高阶格式，同时可以保持原有差分格式的高阶精度。

数值实验结果表明，新的RAD求解器克服了传统近似Riemann求解器的缺陷，既能精确捕捉接触间断和激波，又能大幅提高对剪切层等精细结构的分辨率。

后续的研究中，将针对黏性流动问题验证新型RAD求解器的适用性，同时探索更好的自适应因子，避免对特定问题需要调整经验参数的问题。