基于三维特征线理论的曲面激波流场反设计方法
王 丁,王江峰,*,李龙飞
(1.非定常空气动力学与流动控制工业和信息化部重点实验室,南京 210016;2.南京航空航天大学 航空学院,南京 210016)
0 引 言
乘波气动布局由于其高升阻比、方便进行内外流一体化设计等优势在高超声速滑翔飞行器[1-2]及巡航飞行器[3-4]气动设计领域得到了广泛关注。由于基准流场前缘激波依赖区的设计决定了飞行器腹部下方的流场特性及乘波特性,因此前缘激波依赖区流场的设计是乘波布局设计过程中的重点之一。尽管基于传统二维特征线法及吻切理论的激波流场反问题的求解在近年来已得到充分的研究,但该方法无法有效地求解含有显著三维流动效应的流场,因此针对三维曲面激波流场反问题的求解仍有待进一步的研究。
根据基准流场设计原理的不同,将以往设计方法分为两类进行介绍。第一类方法将三维流场简化为二维流场切片的叠加,属于准三维方法。早期研究所用的基准流场主要包括斜劈流场[5]及圆锥激波流场[6],近年来吻切理论在此类方法中占据主导地位。Sobieczky等[7]提出了吻切锥设计方法,该方法将三维流场等效为吻切面上二维锥形流场切片的叠加,随后又将吻切面流场进一步拓展为任意轴对称流场切片,即吻切轴对称法[8],并在内外流一体化设计领域得到了广泛应用,例如全乘波内外流一体化布局[9-10]、吻切内锥前体进气道一体化布局[11]等。以上方法中,每个吻切面共用同一种流场构型,而吻切流场法[12-13]在每个吻切面内独立设计各自的二维流场,进一步提高了设计的灵活性,该方法近年来在宽速域滑翔飞行器和内外流一体化飞行器设计领域得到了大量应用,例如展向变马赫数乘波体[14-16]、展向变激波角乘波体[17]、多级压缩内外流一体化乘波布局[18-19]、双乘波内外流一体化布局[20-21]。前述方法在设计过程中忽略了流场中的三维效应,为了增强对三维流动效应的模拟能力,实现基于复杂三维激波流场的乘波布局设计,Zheng等[22]提出了多吻切锥设计方法,该方法将吻切面内流场处理为多个不共轴的圆锥流场的组合,从而显著提高了对带有较大横向压力梯度流场的模拟能力。随后,使用流面替代吻切面实现对三维流场的逼近,进一步提出了局部偏转吻切锥方法[23],该方法对带侧滑椭圆锥激波流场、变截面椭圆锥流场的三维流动效应均表现出了良好的模拟能力,但该方法与真正意义上的三维模拟仍有一定区别。文中仅给出了其设计得到的壁面压力分布与数值模拟的对比(最大误差在2%左右),但未披露壁面马赫数的计算误差。
第二类方法是全三维方法,对于已知三维壁面形状的三维基准流场正问题[24-25]来说,求解的关键在于对三维激波的准确模拟,相关数值模拟方法主要分为激波装配法和激波捕捉法两类。激波装配法[26]通过对激波面进行追踪并利用Rankine-Hugoniot关系式求解激波前后信息,保证了激波模拟的准确度,但激波面的追踪过程涉及复杂的网格操作,因此与非结构网格相结合以增强激波装配算法的通用性和鲁棒性是该方法发展的重点之一[27-28]。对于激波捕捉法而言,激波面由计算格式在给定的网格中进行模拟捕捉,因此激波形状无法被精确描述。近似求解一维Riemann问题的通量格式(例如Roe格式及AUSM系列格式等)在低阶激波捕捉格式中应用最为广泛,此类格式计算效率高且物理意义明确,但计算结果中出现的“红宝石”现象、过热现象、全速域计算问题[29-30]及基于维度分裂向多维格式推广时忽略了单元切向物理信息[31]等问题仍有待进一步的研究。此外,基于叠波法的Godunov型大时间步长格式[32]也值得进一步关注,该方法充分考虑了精确解的依赖域,通过波束的线性叠加假设实现了CFL(Courant-Friedrichs-Lewy)数的显著提高,且具有对间断模拟的精度随着CFL数提高而增加的优点。提高激波分辨率的有效途径之一是使用低数值耗散的高阶格式,目前主要包括高阶有限差分格式(例如WENO[33]格式)、基于有限体积的高阶格式(如有限体积高阶WENO格式[34])和有限元类高阶格式(例如DG[35]格式),文献[36]对不同高阶格式的特点及发展给出了详细讨论。基于三维特征线理论的数值算法是三维曲面激波反问题的主要求解方法之一。目前相对较为实用的三维特征线方法主要包括两种:一种是校正六面体双特征线法[37],该方法基于三个初值点,通过求解三个马赫锥的交点得到待求点,Huang等[38]给出了该方法在非均匀来流曲激波流场设计上的应用,但未详细评估该方法的计算误差,且该方法目前仅限于求解激波依赖区流场,尚未见到应用于基准流场其他模块(如压缩区等)的设计;另一种是五面体双特征线方法[39-40],该方法通过沿流线进行时间积分得到待求点,由于该方法要求初值面和求解面相互平行,壁面及激波形状均已知,且需要构造在局部坐标系中分别相差90°的四根双特征线,因此主要应用在内流道流场[41-42]及激波流场[43]正问题的求解中,并不适用于激波流场反问题的求解。
为了克服传统吻切理论在设计全三维曲面激波流场时的缺陷,实现对全三维复杂激波流场反问题的求解,本文基于三维特征线理论重构了描述三维流动的控制方程,并在此基础上发展了用于求解三维激波依赖区流场的全三维设计方法。采用圆锥激波流场、椭圆锥激波流场、小攻角圆锥激波流场和由Bezier曲面描述的一般性曲面激波流场等四个典型算例进行了方法验证。通过与二维特征线方法对比,分析了本文设计方法的计算误差及并行效率。与数值模拟结果对比,验证了本文设计方法对由横向压力梯度及攻角引起的三维流动效应的模拟能力。
1 控制方程
依据三维特征线理论[37],马赫锥及流线上的特征速度满足图1所示的几何关系,其中马赫锥由点S2发出,流线 S1S2为马赫锥的轴线,若线段 S1S2的长度为流动速度V的大小,则线段 S1B1的长度为声速a,其方向与特征法矢n一 致,点 S1和点 A1位于垂直于马赫锥轴线的平面上,线段 S1A1的长度为特征声速c,线段 A1S2的长度为特征速度Vc(式1)的大小。若定义 ∇s为沿流线的变化率算子(式2), ∇c为沿马赫线的变化率算子(式3),则对描述超声速有旋无黏流动的控制方程(式4~8)中的微分算子进行特征分解(式2和式9),可得沿马赫线的控制方程(式10~13)以及沿流线的控制方程(式14~18)。

图1 速度关系与马赫锥Fig.1 Velocity relation and Mach cone
2 基本单元的构造及求解方法
本节通过构造基本单元求解特定点的压力P、密度 ρ 、速度矢量V、压力梯度 ∇P、速度张量 ∇V等17个物理参数。
2.1 基本单元的构型及相关计算几何算法
图2给出了基本单元构型及其求解流程。图中,初值线 D1D2和 D3D4为已知的三维网格线,绿点的物理参数均已知,蓝点 S2为待求点,基本单元包含4条马赫线和1条流线。在单元求解过程中共涉及6个基础算法,下面分别进行介绍。
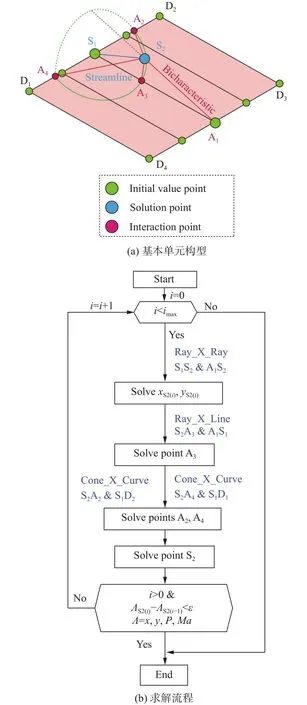
图2 基本单元构型及其求解流程Fig.2 Basic cell and the solving procedure
2.1.1 线性插值及特征线平均物理参数计算方法
假设线段两端点分别为点1和点2,插值点3位于点1和点2之间,则可用式(19~20)所示的线性插值公式计算点3的物理参数,其中d31为点3到点1的距离,d21为点2到点1的距离。在计算特征线平均物理参数时,插值系数取 ξ =0.5。
2.1.2 特征线速度矢量及法矢的计算方法
参考图3,若约定变量上方加双横线代表对矢量进行归一化处理,则流线的方向矢量l可以表示为式(21),马赫线(以线段 S2A3为例)的特征速度、方向矢量l和法矢n可 分别表示为式(22~24),其中dA3S1为点 A3到点 S1的矢量,但对于图2中的马赫线 S2A1来说则是点 S1到点 A1。
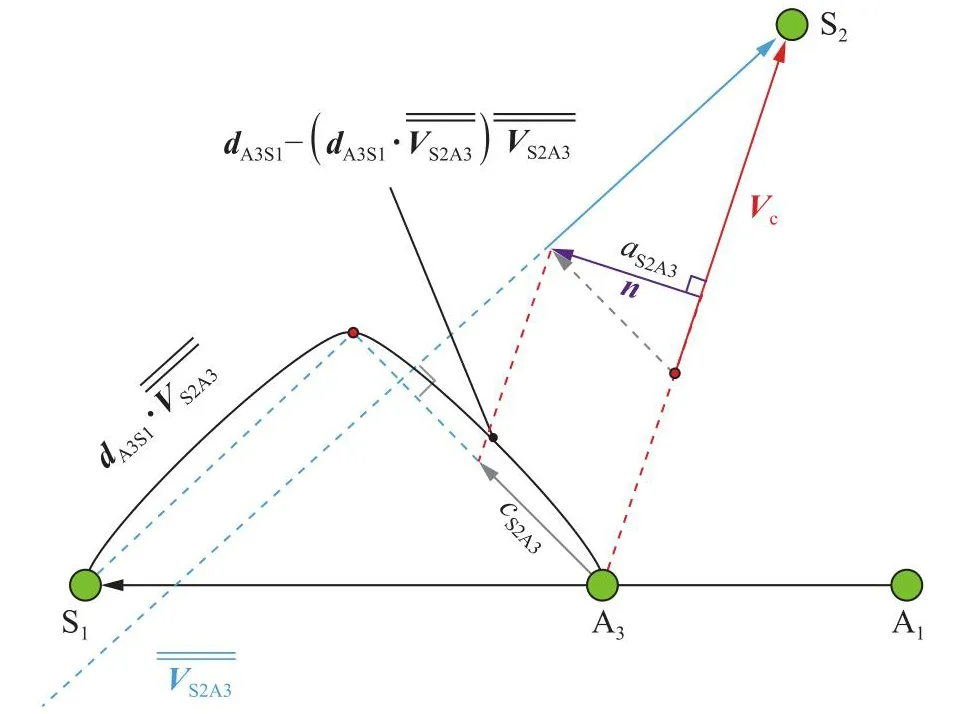
图3 特征速度计算方法Fig.3 Calculation method of the characteristic velocity
2.1.3 Ray_X_Ray算法
该算法用于求解空间两射线的交点坐标。参考图4,以计算两射线 S2A1和 S2A3的交点 S2为例,首先计算两射线 S2A1和 S2A3的方向矢量l,则交点 S2的坐标为式(25),如果点 S2位于对称面边界上,则还需要对计算得到的坐标进行对称面边界校正。这里S2、A1等黑斜体英文字母均表示坐标系原点到对应点的距离矢量。

图4 Ray_X_Ray算法原理Fig.4 Principle of the Ray_X_Ray algorithm
2.1.4 Ray_X_Line算法
该算法用于求解空间射线和直线段的交点。参考图5,以计算射线 S2S1和线段 A1A3的交点 S1为例,首先计算射线 S2S1的方向矢量和线段 A3A1的矢量,点S1物理参数的初值为点 A3和点 A1物理参数的代数平均(式19, ξ =0.5),利用式(26)计算点 S1的坐标,并由式(27)更新插值系数 ξ,最后利用线性插值对点 S1的坐标及物理参数进行更新。通过迭代上述步骤,直到点 S1的坐标变化小于容差 ε ,本文所有算法所用的容差统一取 ε =1.0×10-6。

图5 Ray_X_Line算法原理Fig.5 Principle of the Ray_X_Line algorithm
2.1.5 对称面边界相关算法
对称面边界由一个对称面上任意选取的参考点Qs及 法矢n确 定,n的方向定义为由流场计算域内部指向外部。对称边界条件包括对称面处点参数的校正及镜像点的计算,下面分别进行介绍。
2.1.5.1 对称面镜像点坐标及物理参数的计算
假设已知流场内侧一点 QL,若dLs为 点 QL到点Qs的 距离矢量,则该点关于对称面的镜像点 QR的坐标QR、速度VR、速度张量 ∇VR(若z平面为对称面)、速度张量 ∇VR(若y平面为对称面)、压力梯度 ∇PR,分别按式(28~32)计算,其中矩阵右下角的“L”表示矩阵内的变量取点 QL的值。
2.1.5.2 对称面上点的坐标及物理参数的校正
对于对称面上任一点 Qr,若drs为 点 Qr到点 Qs的距离矢量,则该点校正后的坐标Qrc、 速度Vrc、速度张量∇Vrc( 若z平面为对称面)、速度张量 ∇Vrc(若y平面为对称面)、压力梯度 ∇Prc,分别按式(3 3~37)计算,其中矩阵右下角的“r”表示矩阵内的变量取点 Qr的值。
2.1.6 Cone_X_Curve算法
该算法用于求解已知点发出的马赫锥和初值线的交点,图6为交点的求解流程。参考图7,以交点A4的计算为例,初值线为特征网格线 D1D2(点数为Nspan)。如果存在对称面边界,则初值线在对称面处需要构造Nextend(式38)个镜像点,来统一对称面附近基本单元的计算(如图8所示)。式(39)为马赫线A4S2的特征矢量lA4S2在平面 A4S2S1上的投影。式(40)为矢量dA4S2和投影方向矢量lproj分别与矢量dS1S2的夹角的差值,用来评估当前点与真实交点的误差。假设点 S1在初值线上的指标为istart,沿初值线由点 S1向点 D1方向的搜索步长为istep=1,利用istart和istart+istep点 按插值系数 ξ =1.0×10-4进行线性插值,得到istart点在初值线上极小邻域内的一点,并用该点计算 d θstart,且有 d θstart<0。交点的求解过程分为两步:1)由点 S1沿初值线向点 D1方向搜索,在每点计算式(39~40),直到相邻两点 d θi·dθi-istep<0,则交点位于该区间内;2)按照式(41~42)进行加权插值,其中初始的 ξL=0对应于初值线上指标为i-istep的点,ξR=1对应 于 指标为i的 网 格点 , 在迭 代 过 程中 , ξL、ξR、 d θL和 d θR按照图6所示流程进行更新,直到收敛。

图6 Cone_X_Curve算法求解流程Fig.6 Flow chart of the Cone_X_Curve algorithm
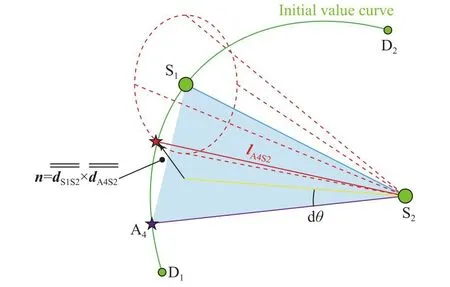
图7 Cone_X_Curve算法原理Fig.7 Principle of the Cone_X_Curve algorithm
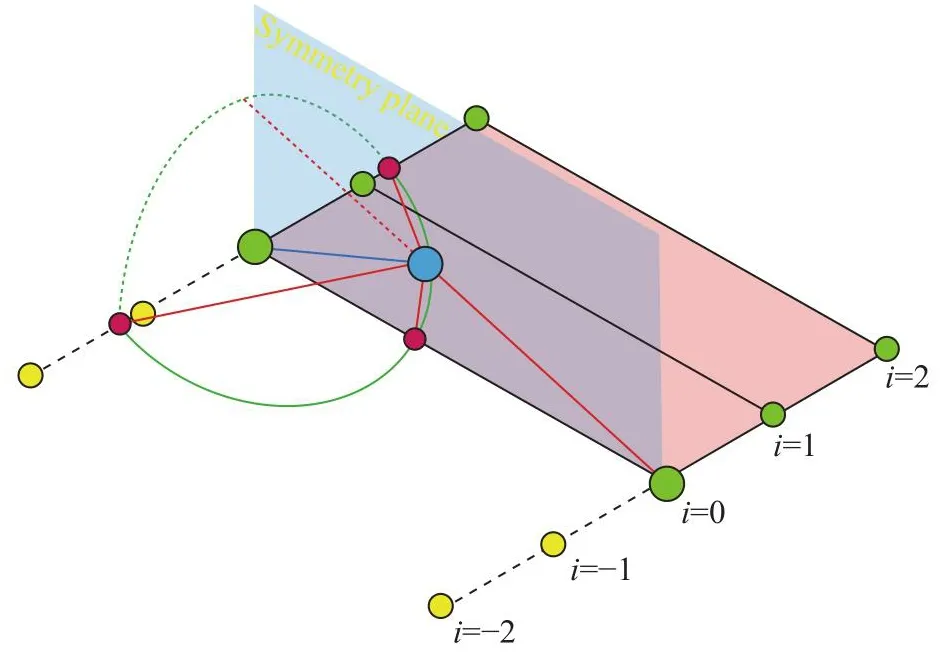
图8 初值线镜像点的构造Fig.8 Construction of the mirror points of the initial value curve
2.1.7 基本单元的求解流程
基于以上6个基本算法,基本单元求解的流程可以表述为:1)用点 S1的物理参数给点 S2赋初值,该两点为流线的两端点;2)利用Ray_X_Ray算法计算流线 S1S2和马赫线 A1S2交点 S2的坐标;3) A3的物理参数的初值采用点 A1和点 S1的平均值,然后利用Ray_X_Line算法计算马赫线 S2A3和线段 S1A1的交点A3的坐标,并利用线性插值计算点 A3的物理参数;4)利用Cone_X_Curve算法插值求解点 A2和点 A4的坐标及物理参数;5)求解线性方程组,如果该点位于对称面边界上,则需要利用对称面边界对求解结果进行校正;6)重复步骤b~e直到待求点的空间坐标、压力和马赫数在两次迭代间的变化小于给定的容差 ε,或总迭代数大于预设值imax。最终构成的线性方程组由17个方程构成,如表1所示,其中马赫线 S2A1和S2A3按式(10~13)分别提供4个方程,沿马赫线 S2A2和S2A4的式(10~13)相减提供4个方程,流线 S1S2按式(14~18)提供最后的5个方程。

表1 基本单元的线性方程组Table 1 Linear equations of the basic cell
2.2 控制方程的离散及线性方程组的求解
2.2.1 控制方程的离散
首先介绍控制方程(10~13)和(14~18)的离散:沿马赫线由任一点1到点2(待求点)对微分方程(10~13)进行时间积分,并将特征算子 ∇c转化为差分项可得式(43~46);沿流线由任一点1到点2(待求点)对微分方程(14~18)进行时间积分,并将特征算子 ∇s转化为差分项可得式(47~51)。
式(43~51)中: δt表示变量t的一个增长量;变量上方的单横线表示该段特征线上的参数平均值(式19)。将式(43~49,51)中的时间积分项处理为(52~59)。其中,马赫线和流线的时间项分别按式(60~61)计算;δl为特征线的长度,且定义特征线上的速度矢量方向为由初值点指向待求点时 δl为正值,否则为负值。离散后总的控制方程见附录。
下面介绍三种不同的 ω 取值方案。
2.2.1.1 “ ω 01”方案( ω1=0, ω2=1)
该方案假设速度张量 ∇V和压力梯度 ∇P沿特征线为常数,并用待求点的速度张量 ∇V和压力梯度 ∇P作为整个特征线上的值来进行时间积分。
2.2.1.2 “ ω 12”方案( ω1=1/2, ω2=1/2)
该方案假设速度张量 ∇V和压力梯度 ∇P沿特征线随运动时间为线性变化。
2.2.1.3 “ ω -V”方案( ω1和 ω2为特征速度和距离的函数)
将沿马赫线和流线的特征速度的大小分别表示为式(62~63),那么速度张量 ∇V和压力梯度 ∇P的各分量(统一用 Λ表示)沿特征线上点1到点2的时间积分可以表示为式(64~68),该式的解析解为式(69~70)。为了加强数值稳定性,将式(69~70)统一用式(69)的四阶泰勒展开(式71~73)表示。
当b2≠0时,
当b2=0时:
“ ω 12”和“ ω -V”方案中均用到了初值点1的速度张量 ∇V和压力梯度 ∇P,在流场的计算过程中,采用最小二乘法进行计算。假设在流场中与点1由网格线直接相连的点有m个,若记点1的待求变量为∇Λ0,则由式(74~78)所示的最小二乘法计算 ∇ Λ0。其中,di为点1到第i个相邻点的距离矢量, Φi为最小二乘法的残差函数,f为最小二乘法的目标函数。
2.2.2 线性方程组的求解
将表1中的线性方程组表示为Ax=b,其具有如下特点:1)系数矩阵为病态矩阵,使得A和b的小误差会导致x产生较大的误差;2)系数矩阵的最小奇异值(第17个奇异值,线性方程组的秩为17)与次小奇异值(第16个)相差较大。以上两个特点使得该线性方程组的求解存在较大的稳定性问题,需要进行特殊处理。
本文基于Tikhonov正则化和Lagrange插值方法发展了适用于该线性方程组求解的Tikhonov-Lagrange拟合法。若线性方程组系数矩阵的奇异值分解为式(79),则参考Tikhonov正则化方法[44],本文构造的方程组的解为式(80),其中对角矩阵 Σ*的第i个对角项为式(81),r为调节指数,当α为0时,方程组的解恢复为未经任何修正的原始解。以第4.1节圆锥激波算例中的第一个基本单元的求解为例,时间积分 选 “ ω 01” 方 案 , 则 求 解 的 变 量P、 ρ和V随α在间的变化曲线如图9左侧所示。为了防止坐标轴过多产生干扰,图中隐去了5个变量的y轴。当r=1时,P、ρ和w曲线是近似重合的;当r=2时,u和v曲线也近似重合。r=1 时的速度分量u和w在α=-Σ1r7附近出现震荡,则系数矩阵的奇异值分解的小误差会引起所求物理量的较大误差,这也是使用高斯消去法直接求解此类线性方程组会有严重的稳定性问题的原因,但这一震荡情况在r=2得到显著改善。对r=2的变化曲线的光滑部分进行采样,建立P、ρ和V的Lagrange插值曲线,则拟合曲线在α=0处的值即为Tikhonov-Lagrange拟合法得到的线性方程组的解。本文在α=0的左右两侧按照式(82~85)各取对称的7个点,当采样点α确定时,对应的解由式(80~81)解出,从而完成5个变量(P、ρ和V)的Lagrange插值曲线的拟合。由于压力梯度和速度张量不是流场设计中的关心变量,因此不进行拟合求解。

图9 典型变量随系数的变化曲线Fig.9 Variation curves of typical variables with the coefficient
3 三维曲面激波依赖区设计方法
本节包含曲面激波的离散及网格面的推进算法两部分内容。
3.1 曲面激波的离散及数值解存在的必要条件
本文关注的重点在于激波流场求解算法本身,因此不对存在反问题解的激波曲面的数学表达式及最优网格单元划分方法做深入探讨。简单起见,对于圆锥及椭圆锥等曲面激波直接采用三维建模软件生成模型,并在网格划分软件中离散成均匀的四边形网格。对网格点周围相邻的四个四边形网格单元的法矢进行反距插值可以得到网格点处的法矢。对于复杂的激波曲面算例采用3 × 1阶Bezier曲面进行准确描述(见式86~88),其中 P0,0等为Beizer曲面的控制点。将Bezier曲面均匀离散为Nu×Nv个点(如图10所示),则第(i,j)个网格点的参数坐标为(iδu,jδv),参数步长的定义见式(89~90),网格点处单位法矢的计算见式(91)。对于离散后的激波网格,网格点的波后物理参数可由Rankine-Hugoniot关系式(式92~98)计算得到,其中下标1代表波前参数,下标2代表波后参数,下标n代表激波曲面的法向,下标t代表激波曲面的切向。
对于得到的离散激波网格,激波反问题有解需要保证两个条件,从而保证待求点可解:1)激波流场本身是存在的且流场内马赫波不会汇聚成激波;2)流场内任一点的基本单元均能够成功建立。下面针对这两个条件进行展开讨论。
要使激波流场是存在的,则需要使激波曲面上任一点的波前法向马赫数大于1,且该点的激波角 β 小于脱体激波角。参考图10,由波前法向马赫数大于1可得式(99),其中激波角由式(100)计算。该点的脱体激波角对应于波后气流偏折角 θ的极值,即式(101),因此激波角的范围可表示为式(102~105)。此外,激波曲面波后任一点向下游发射的马赫锥必须与激波曲面相交,该条件保证了图2中逆马赫线A1S2存在,该条件可表示为式(106)。代入波后马赫数及对应的马赫角α2的计算公式(107~108),可化简为式(99),即只要波前法向马赫数大于1,则该条件成立。要使流场内马赫波不会汇聚成激波,需要约束激波曲面在两个相互正交的典型方向上的曲率,参考图11,第一个方向是来流速度V1及激波曲面法矢n组成的平面与激波曲面的交线方向,由正交关系可得第二个方向。以第一个方向为例讨论激波曲率对马赫线汇聚点位置的影响。点 A2为点 A1在激波曲面上极小邻域内的一点,两点间距为 δs, 激波曲面在点 A1处的曲率中心为点 C1,曲率半径为R,两点发出的逆马赫线交于点 D1(若两条逆马赫线平行,则交点在无穷远处),线段 A1D1的长度为dA1D1,则由图11中的几何关系可得式(109~110),以上两式按照式(111~112)的推导可得式(113),其中波后马赫角α2-A1及气流偏折角 θA1的计算公式见式(108,101)。显然两马赫线交点的距离与当地激波曲率半径成正比。若该交点落在流场内,则流场内存在马赫波汇聚为激波的现象,因此该式对激波曲率半径的最小值进行了约束。对于反问题而言,由于壁面位置在求解前是未知的,因此如何在该条件的基础上发展激波形状的显式约束表达式是后续研究的重点之一。

图10 激波曲面的离散Fig.10 Discretization of the shock surface

图11 激波曲率的估计Fig.11 Estimation of the shock curvature
离散激波流场有解等效为流场中所有离散单元有解。下面介绍流场内任一点的基本单元能够成功建立的必要条件。图12给出了展向相邻两网格单元及数值基本单元的结构与理想情况下典型角度间的关系。式(114)和式(115)保证了交点 S2的存在性,显式约束了线段 S1A1的方向,同时隐式约束了其长度,其中式(114)表示点 S1位于点 A1发出的逆马赫锥内,式(115)表示流线 S1S2与马赫锥的交点 S2位于当前网格层的下游。为了完成基本单元控制方程的构造,还需要保证马赫线 S2A4及 S2A2与初值线 D1D3的交点存在(参考图12),该条件难以显式给出。但当四边形D1S1A1D4和S1D3D6A1为激波网格单元时,可以根据图12中建立的理想化角度关系对激波初值面上网格长宽比的理想值给出估计。假设点 S1和点 A1的物理参数一致,则流线 S1S2的长度 δsl、线段 S1A1的长度 δl和线段 S1A4的长度 δw间满足式(116)和(117)的关系,合并得式(118),其中 ta n(β-θ)由式(119)计算。为了方便起见将称为理想长宽比。对于激波单元S1D3D6A1来说,当激波网格长宽比小于理想长宽比时,交点A4位于激波单元的横边 S1D3之内,即基本单元的求解被限制在展向相邻两激波单元内,因此该参数为激波面网格的划分方案提供了直观的参考。图13给出了典型马赫数下激波网格长宽比随激波角的变化,其中虚线为激波角取马赫角时的极限值。随着激波角的增大,理想长宽比逐渐降低,即当激波单元横向宽度不变时,纵向长度需要不断降低来保证数值解存在。
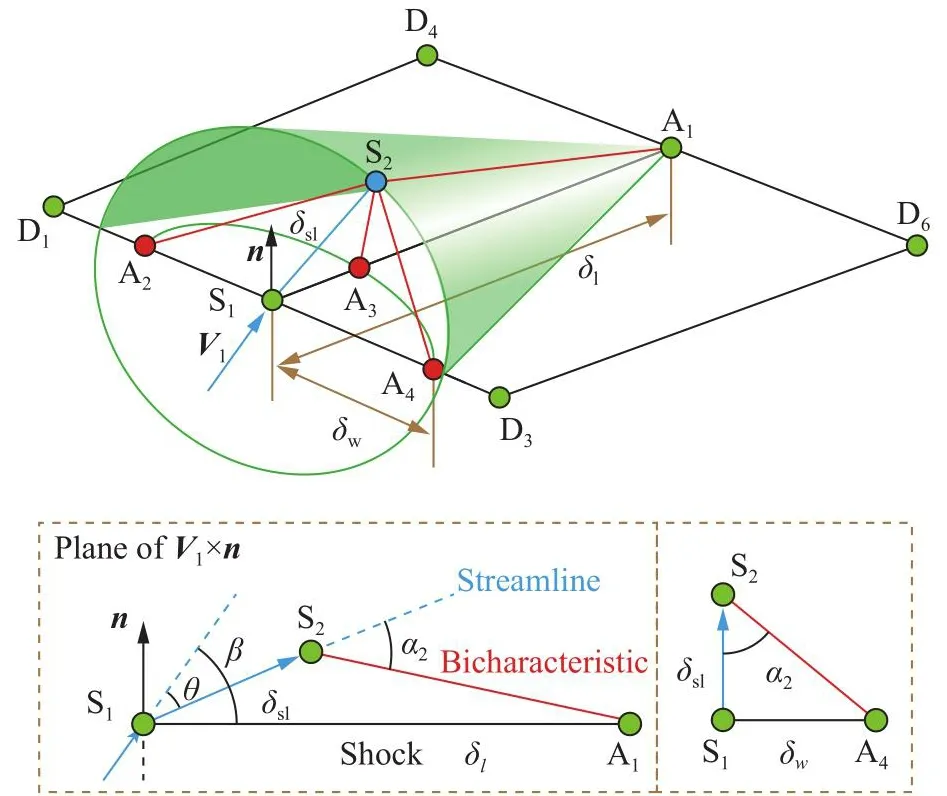
图12 纵向步长的预估方法Fig.12 Prediction method of the lengthwise step
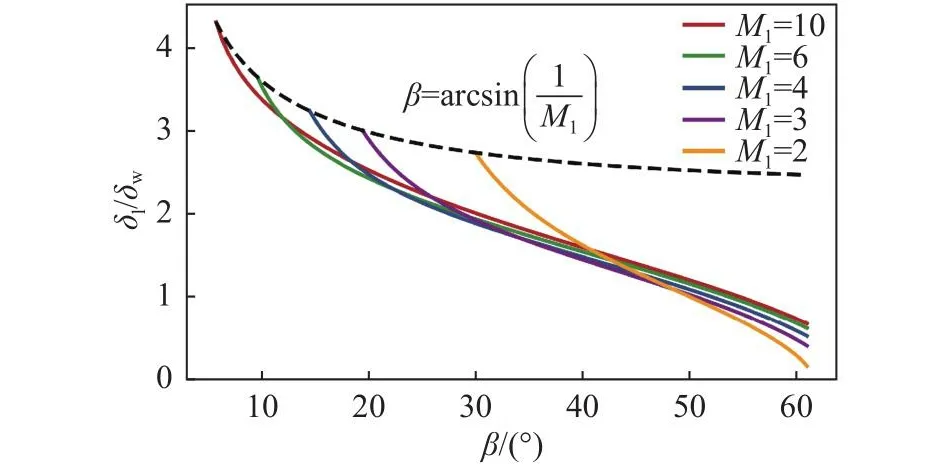
图13 理想长宽比与激波角的关系Fig.13 Relationship between the ideal length-to-width ratio and the shock angle
3.2 网格面的推进及计算
图14所示为网格面的推进原理,具体流程如图15所示。图14中的坐标系标注了图15中i(纵向)、j(展向)和k(层推进方向)循环指标对应的方向。以3 × 4个网格点的激波面网格为例,此时Nlengthwise=4、Nspanwise=3、mmax为每一层求解时的最
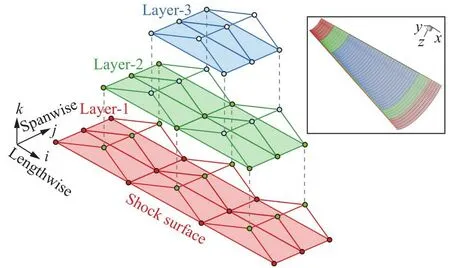
图14 网格面推进的原理Fig.14 Principle of the mesh plane advancing

图15 网格面推进流程Fig.15 Flow chart of the mesh plane advancing
大迭代数。对于“ ω 01”方案,由于不涉及前一层网格的速度张量及压力梯度的值,因此mmax=1。对于另外两种格式,则需要通过当前层的物理参数校正前一层的速度张量及压力梯度,本文给定mmax=30。网格推进的流程为按照i(纵向)、j(展向)和k(层推进方向)三个循环指标反复求解基本单元。计算流程中的残值定义为式(120),其中i、j和k指标遍历当前网格面的所有网格点。由于沿展向求解基本单元时,单元间相互独立,因此该部分循环可以进行OpenMP并行加速。
4 算例验证及结果讨论
本文选取圆锥激波依赖区设计问题、椭圆锥激波依赖区设计问题、小攻角圆锥激波依赖区设计问题和基于Bezier曲面的三维曲面激波依赖区设计问题4个算例来分别讨论和验证以下内容:三维设计方法的计算误差和并行效率、对由横向压力梯度和攻角引起的三维流动效应的模拟能力、当前算法对一般性曲面激波反问题的求解能力。
4.1 圆锥激波依赖区设计验证
算例为半锥角15°的圆锥激波流场的设计(如图16所示)。坐标系原点位于左侧半径为100 mm的圆截面圆心处,激波锥长度为1 000 mm,来流条件见表2。该算例用于验证当前设计方法对三维激波依赖区的设计能力,讨论不同求解策略设计结果的计算误差,并在此基础上讨论当前并行策略的计算效率。
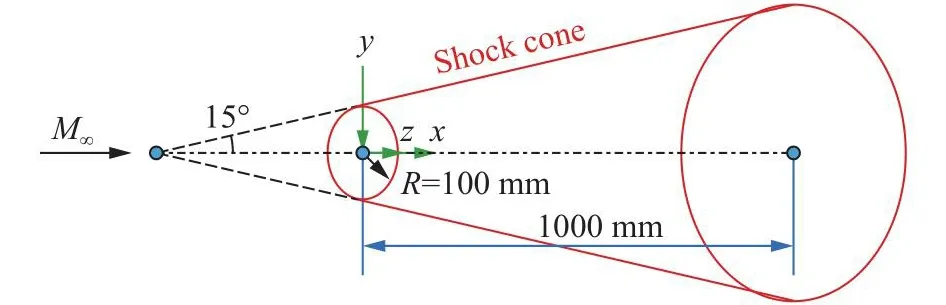
图16 圆锥激波计算模型Fig.16 Computational model of the conical shock

表2 来流参数Table 2 Inflow parameters
图17所示为三维特征线所用的激波面网格(红色网格,纵向 × 展向 = 100 × 50)和计算得到的流场网格。其中,激波面为位于yz坐标系第四象限的1/4圆锥,蓝色部分为反设计得到的壁面网格,流场网格量约为24.3万,两个对称面边界分别为y= 0 mm和z=0 mm平面。图18所示为“ ω 01-TL”方案计算得到的流场,实体部分为计算得到的流场压力分布,切面由镜像后的完整流场中截取而来。由图可知,当前方法能够得到光滑的流场设计结果。

图17 激波面网格及设计所得的流场网格Fig.17 Shock-surface mesh and the designed flow-field mesh
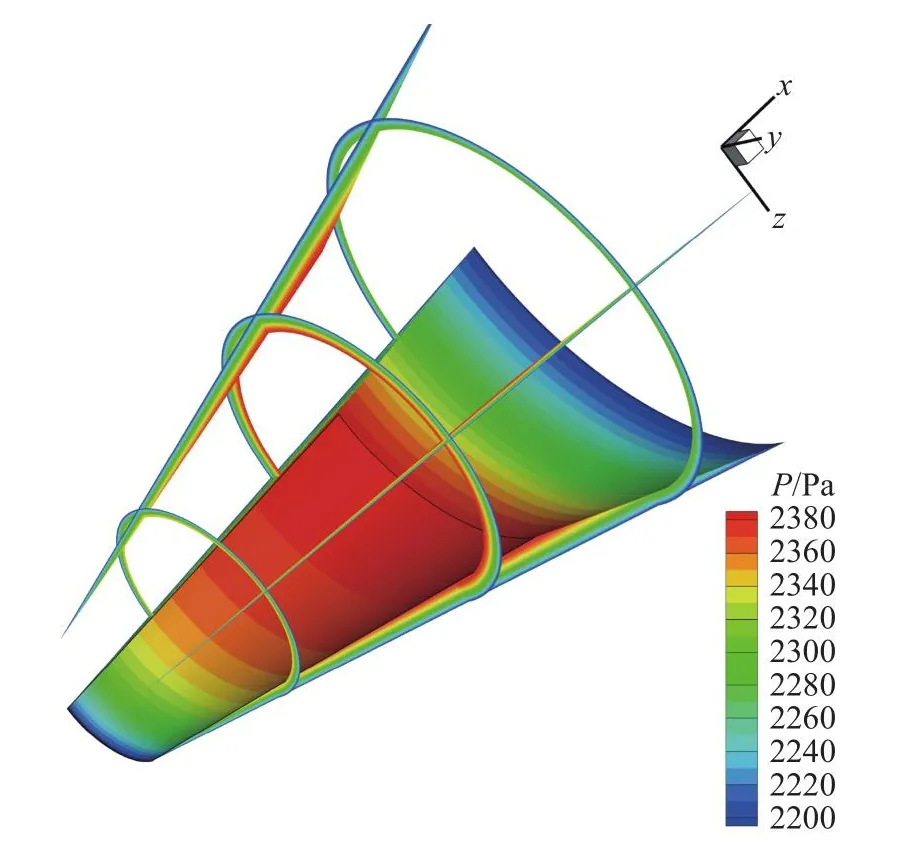
图18 设计所得流场的压力分布Fig.18 Pressure distribution of the designed flow field
图19所示为四种计算策略计算得到的壁面压力及马赫数分布。四种计算策略由不同时间积分、调节指数和线性方程组求解方法组合得到(如表3所示,其中“FP”和“TL”为该表右侧列出的线性方程组求解方法的简写)。由于列主元消去法无法稳定求解当前流场,因此选择全主元消去法(采用开源矩阵库Eigen中的fullPivLu函数进行求解)作为对比项。

表3 计算策略Table 3 Calculation methods
图19中实线部分的激波面网格量为100 × 50,虚线部分的激波面网格量为50 × 50。黑色实线为激波线上取100个点时的二维特征线方法的计算结果。如果认为与二维特征线的计算结果越近则计算精度越高,则可以得到以下结论:1)四种方法的计算精度排序由高到低依次为:“ ω 12-TL” ≈“ ω -V-TL”>“ ω 01-TL” >“ ω 01-FP” ;2)时间积分方案“ ω 12”与“ ω 01”对当前算例的计算结果几乎没有区别;3)使用Tikhonov-Lagrange拟合法求解线性方程组相比fullPivLu方法能够有效地提高计算精度,并且改变网格量对计算结果的影响较小,而fullPivLu方法则对网格量极为敏感,使用50 × 50的粗网格和100 × 50的精细网格的计算结果完全不同,且粗网格计算时反倒得到较好的结果;4)除了“ ω 01-FP”方案,其余三种方案计算得到的壁面尾部马赫数误差低于0.16%、压力误差低于0.17%,因此能够满足一般流场的设计需求。
“ ω 12-TL”和“ ω -V-TL”方案考虑了压力梯度和速度张量沿特征线的变化,因而获得了更为精确的结果,但当求解前一层网格面(图20中第i-1层)尾部格点的压力梯度和速度张量时,由于下游点6和点7的缺失,导致该点处实际所用的模板与周围点存在较大差异,难以得到光滑的最小二乘解,导致了图19中计算结果在尾部的振荡,从而引发稳定性问题,因此改良前一层网格的压力梯度及速度张量的计算方法是后续研究的重点之一。基于以上研究结果,选择“ ω 01-TL”作为后续激波依赖区的设计方法。
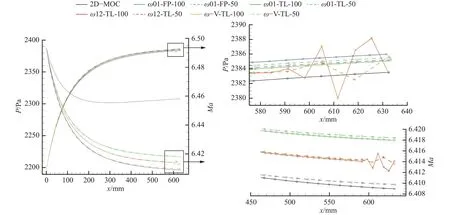
图19 不同计算方法设计结果的对比Fig.19 Comparison of the results from different calculation methods

图20 网格面尾部点的最小二乘计算模板Fig.20 Calculation stencil of the least square method for the ending points on the mesh surface
选择网格量为100 × 50的激波面网格来研究本文并行策略的计算效率,计算格式为“ ω 01-TL”,测试所用CPU为Intel i7-9750H,对比结果见表4。计算结果表明,本文提出的设计方法具有较高的并行效率。

表4 并行计算加速比和计算效率Table 4 Speedup and efficiency of the parallel computation
4.2 椭圆锥激波依赖区设计验证
算例为椭圆锥激波依赖区的设计(图21所示)。椭圆半锥角分别为15°和17°,坐标系原点位于左侧椭圆截面的中心,且距椭圆锥顶点200 mm,激波锥的两截面间距为1 000 mm,来流条件见表2。图22为所用的激波面网格(红色网格,纵向×展向 = 100 × 50),两个对称面边界分别为y= 0 mm和z= 0 mm平面,右侧为计算得到的流场网格,蓝色部分为反设计得到的壁面形状。流场的压力分布如图23所示。本算例用于验证当前设计方法对由横向压力梯度引起的流场三维效应的模拟能力。

图21 椭圆锥激波计算模型Fig.21 Computational model of the elliptical-cone shock
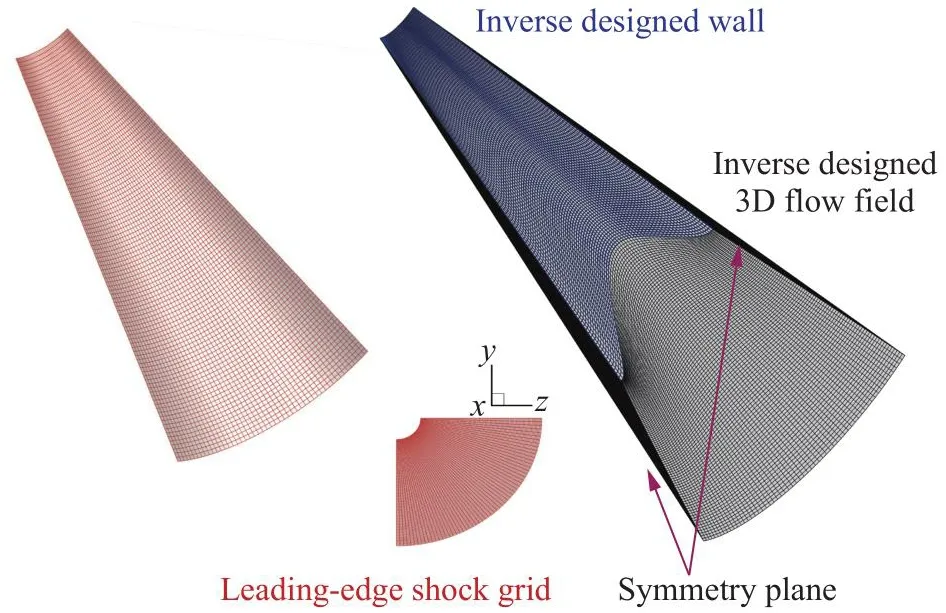
图22 激波面网格及设计所得的流场网格Fig.22 Shock-surface mesh and the designed flow-field mesh
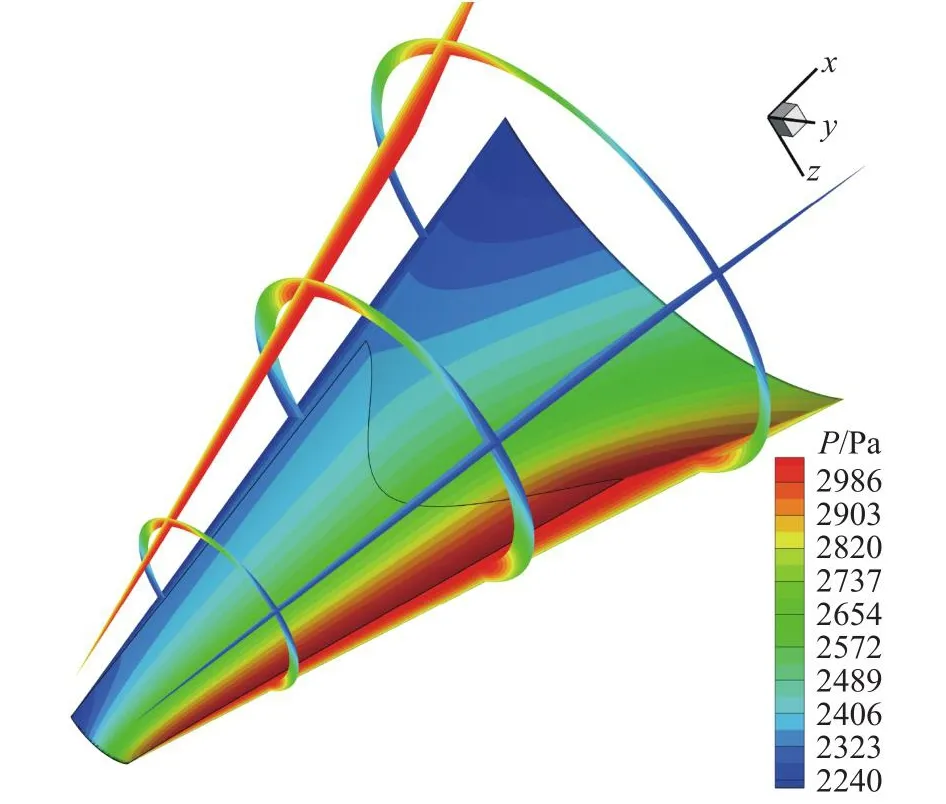
图23 设计所得流场的压力分布Fig.23 Pressure distribution of the designed flow field
为了验证本文设计方法的准确性,采用商业软件Fluent对反设计得到的壁面在表2来流条件下进行无黏数值模拟,计算格式为AUSM+,网格如图24所示,网格量约为136万。图25所示为沿x轴x= 240 mm和x= 500 mm切面的无量纲压力云图对比,其中CFD表示Fluent给出的数值模拟结果,3D-MOC为本文的设计方法,可以看到两种方法计算得到的截面压力分布基本一致,激波轮廓在相接处吻合良好。图26给出了两切面对应的壁面压力分布和马赫数分布,两种方法计算得到的压力分布曲线几乎重合,最大误差位于z= 0 mm(椭圆截面短轴)位置处。相比而言,两种方法计算得到的马赫数有较大的误差,且最大误差同样位于z= 0 mm处。表5给出了z=0 mm处具体计算数值的对比,可以看到两截面处的最大压力误差不超过0.3%,最大马赫数误差不超过1%,能够满足一般的飞行器设计需求。

表5 计算误差对比Table 5 Comparison of the calculation errors

图24 CFD计算网格Fig.24 Computational grid of CFD
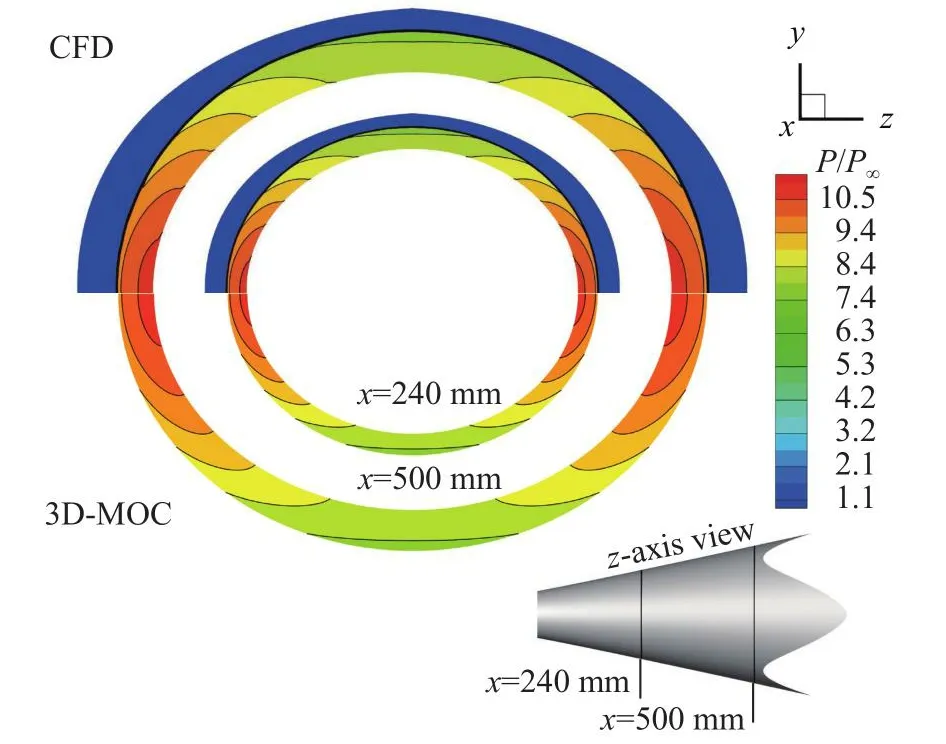
图25 轴向两切面压力分布对比Fig.25 Comparison of pressure contours in two slices along the axial direction

图26 轴向两切面压力及马赫数分布对比Fig.26 Comparison of wall pressure and Mach number distributions in two slices along the axial direction
4.3 有攻角圆锥激波依赖区设计验证
算例为攻角α= 3°、半锥角15°的圆锥激波依赖区的设计(如图16所示),几何参数与4.1节一致,其余来流条件与表2一致。图27为所用的激波面网格(红色网格,纵向 × 展向 = 100 × 100),对称面边界为z= 0 mm平面,右侧为计算得到的流场网格,网格量约48.5万,蓝色部分为反设计得到的壁面形状。流场的压力分布如图28所示。本算例用于验证当前设计方法对由攻角引起的流场三维效应的模拟能力。

图27 激波面网格及设计所得的流场网格Fig.27 Shock-surface mesh and the designed flow-field mesh

图28 设计所得流场的压力分布Fig.28 Pressure distribution of the designed flow field
采用如图29所示的网格对设计得到的壁面流场进行数值模拟,网格量约为145万。图30所示为沿x轴x= 120 mm和x= 380 mm切面的无量纲压力云图的对比。可以看到,两种方法计算得到的截面压力分布基本一致,激波位置在相接处吻合良好。图31给出了两切面对应的壁面压力分布和马赫数分布,两种方法计算得到的压力分布曲线几乎重合,但马赫数分布有一定差异。壁面压力和马赫数的最大误差均位于y= 0 mm位置处。表6给出了y= 0 mm处具体计算数值的对比,可以看到,两截面处的最大压力误差约0.3%,最大马赫数误差不超过1.7%,能够满足一般的飞行器设计需求。

表6 计算误差对比Table 6 Comparison of the calculation errors
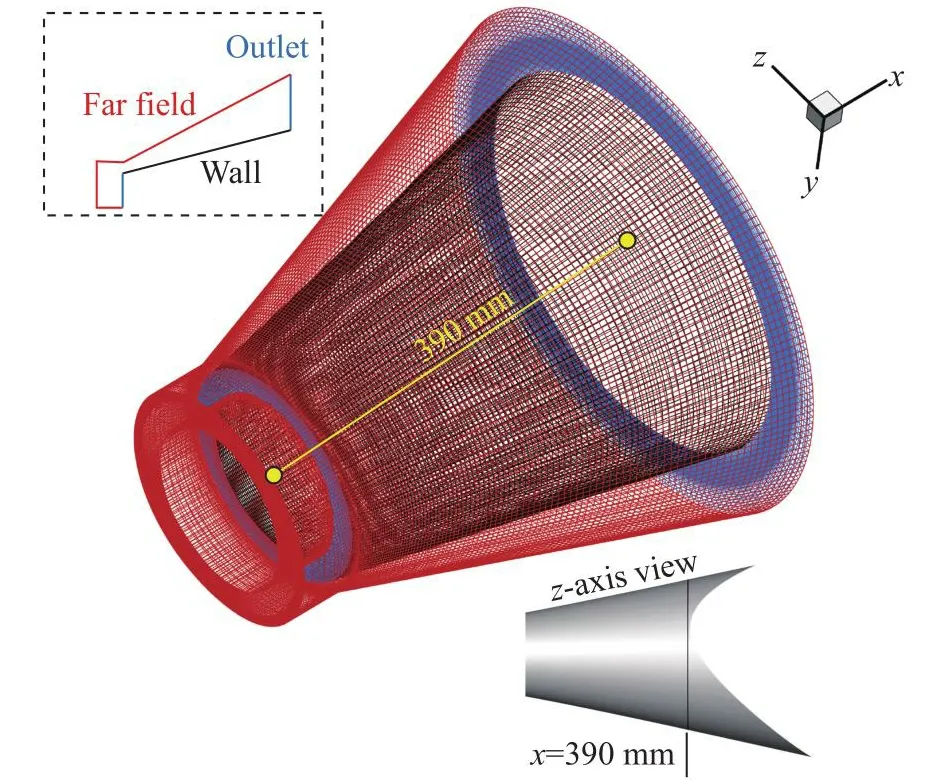
图29 CFD计算网格Fig.29 Computational grid of CFD
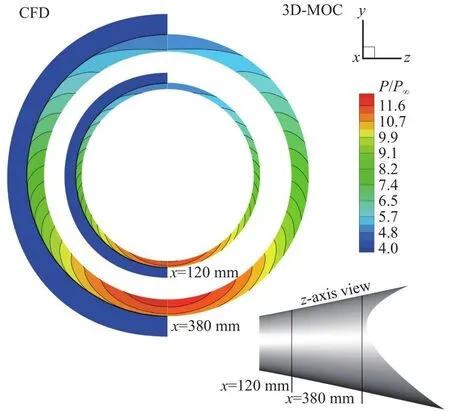
图30 轴向两切面压力分布对比Fig.30 Comparison of pressure contours in two slices along the axial direction
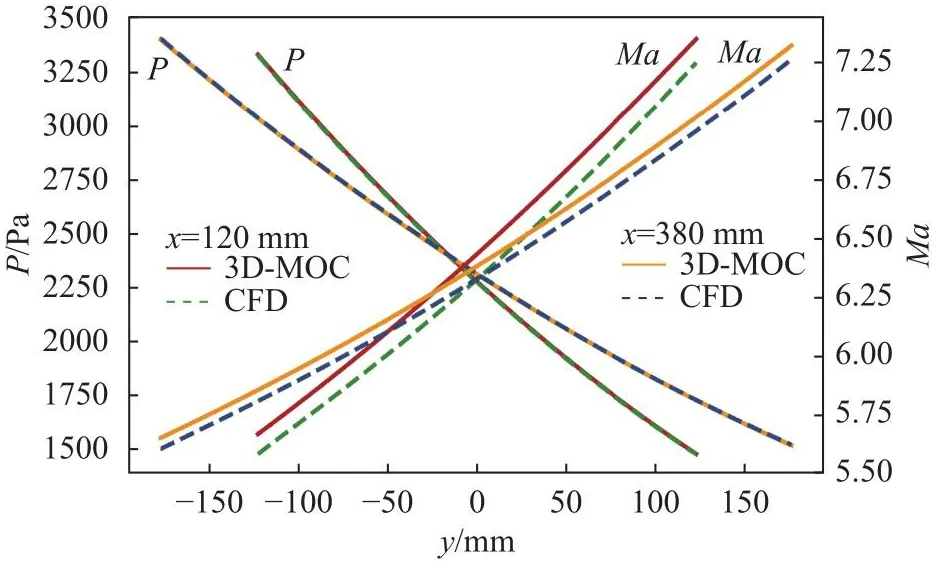
图31 轴向两切面压力及马赫数分布对比Fig.31 Comparison of wall pressure and Mach number distributions in two slices along the axial direction
4.4 一般性三维曲面激波依赖区设计验证
算例为一般性曲面激波依赖区的设计验证,采用3 × 1次Bezier曲面构造激波形状,式(121)为Bezier曲面的控制点,来流条件见表2。图32为所用的激波面网格(红色网格,纵向×展向 = 100 × 50),两个对称面边界分别为y= 0 mm和z= 0 mm平面,右侧为计算得到的流场网格,蓝色部分为反设计得到的壁面形状。流场的压力分布如图33所示。
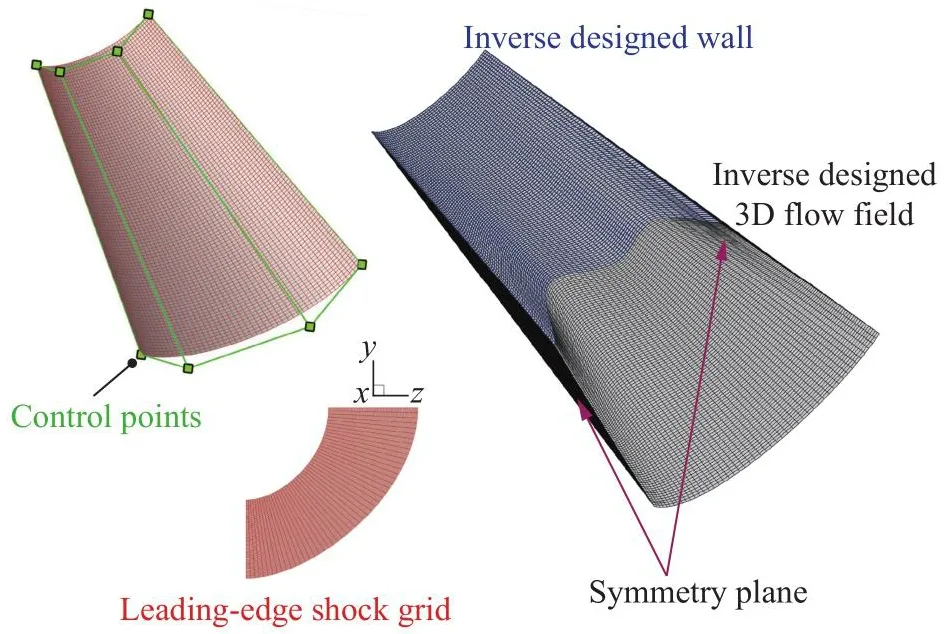
图32 激波面网格及设计所得的流场网格Fig.32 Shock-surface mesh and the designed flow-field mesh
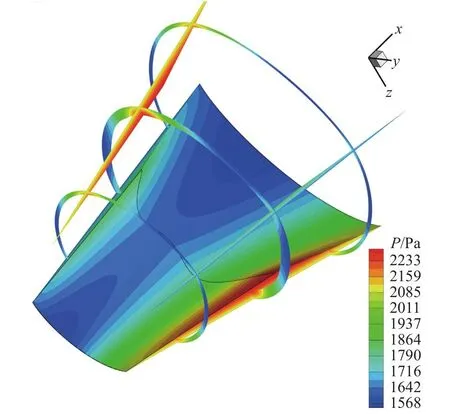
图33 设计所得流场的压力分布Fig.33 Pressure distribution of the designed flow field
采用图34所示的网格对设计得到的壁面流场进行数值模拟,网格量约为229万。图35所示为沿x轴x= 200 mm和x= 450 mm切面的无量纲压力云图对比,可以看到两种方法计算得到的截面压力分布基本一致,激波轮廓在相接处吻合良好。图36给出了两切面对应的壁面压力分布和马赫数分布。两种方法计算得到的压力分布曲线几乎重合,x= 200 mm和x= 450 mm切面的最大压力和马赫数误差分别近似位于z= 127 mm和z= 147 mm位置处。表7给出了最大误差处具体计算数值的对比。可以看到,两截面处的最大压力误差不超过0.2%,最大马赫数误差不超过1.3%,能够满足一般的飞行器设计需求。

图34 CFD计算网格Fig.34 Computational grid of CFD

图36 轴向两切面压力及马赫数分布对比Fig.36 Comparison of wall pressure and Mach number distributions in two slices along the axial direction

表7 计算误差对比Table 7 Comparison of the calculation errors
5 结 论
本文基于三维特征线理论,提出了一种针对三维曲面激波流场的反设计方法。首先基于特征分解重构了三维流场的控制方程,针对控制方程的离散形式发展了三种不同的时间积分策略,并提出了能够稳定求解基本单元线性方程组的Tikhonov-Lagrange拟合法。通过与二维特征线方法及数值模拟结果对比,分析了当前设计方法对典型三维激波流场的计算误差及并行效率。结论如下:
1)利用圆锥激波流场算例对比了不同计算方案对设计结果的影响。一方面,“ ω 12”和“ ω -V”时间积分方案给出了基本一致的壁面压力和马赫数分布,且其误差约为“ ω 01”方案的一半,但两种格式在每个推进层的末尾由于最小二乘计算模板的变化容易产生数值振荡。另一方面,针对线性方程组的求解,本文提出的Tikhonov-Lagrange拟合法在网格加密前后能给出规律基本一致的壁面参数分布,而标准的列主元消去法无法稳定计算流场,全主元消去法对于激波面的网格量较为敏感,无法给出一致的计算结果,因此本文提出的Tikhonov-Lagrange拟合法在稳定求解控制方程组方面具有较大的优势。
2)采用本文提出的“ ω 01-TL”方案研究了当前设计方法的并行计算效率。针对激波面网格为100×50的圆锥激波流场算例,当并行核数为6时计算时间为 9 min 53 s,加速比为4.24,并行效率为70.7%,因此本文提出的设计方法具有较高的并行计算效率。
3)针对椭圆锥激波流场算例、小攻角圆锥激波流场算例及由Bezier曲面描述的一般性曲面激波流场算例,验证了本文设计方法对三维流动效应的模拟能力。与无黏数值模拟结果相比,椭圆锥激波流场在x= 240 mm和500 mm切面处的最大压力误差不超过0.3%,最大马赫数误差不超过1%;小攻角圆锥激波流场在x= 120 mm和380 mm切面处的最大压力误差约0.3%,最大马赫数误差不超过1.7%;Bezier曲面激波流场在x= 200 mm和450 mm切面处的最大压力误差约0.2%,最大马赫数误差不超过1.3%。因此,本文提出的设计方法能够针对典型三维曲面激波流场的反问题给出合理的设计结果。
附录A

