软土地区钢顶管施工引起的地表变形规律

李江

摘 要：为研究软土地区钢顶管施工引起的地表变形规律，以东莞某输水工程为背景，分别采用预测公式、数值模拟和现场监测的方法对顶进过程中引起的地表变形进行了计算和监测，以期得到顶进过程中纵、横方向的地表变形规律。首先推导出了基于顶进间隙的地表变形预测公式并计算出顶管施工可能产生的最大竖向位移为14.1 mm，此变形量在规范允许路面沉降范围内（≤20.0 mm），无须进行土体加固等措施；然后采用数值模拟的方法建立有限元模型对顶进导致的地表变形进行了计算，并就减轻地表变形的方法进行了讨论；最后与现场监测的结果进行了对比分析。结果表明：3种方法得到的变形曲线形状除了顶管轴线处地表峰值位移（数值模拟数值为13.7 mm，现场监测为15.2 mm）有稍许差异外，整体基本一致；顶管顶进时，横向监测断面的沉降槽呈“V”形，最大沉降值在顶管中心轴线处，随着距离中心轴线越远，沉降值越小，最后趋于0；纵向监测断面呈倒“S”形，大致可分为顶进前土体的隆起，顶进中土体的沉降，顶进后土体轻微回隆，顶进后土体稳定4个阶段；在顶管施工前可以对地表变形进行预测和数值模拟计算，结合预测和模拟计算的结果，通过合理的设置顶推力、注浆压力以及必要的土层加固来控制土体的变形。提出的预测公式具有概念清晰、可操作性强的特点，在软土地区适应性好，后续类似工程可以采用。研究成果可为软土地区类似顶管工程施工诱发的地面沉降进行预测及变形控制提供科学参考。

关键词：钢顶管；地表变形；预测公式；数值模拟；现场监测；顶进间隙

中图分类号：TU 991

文献标志码：

A

文章编号：1672-9315（2023）06-1149

-09

DOI：10.13800/j.cnki.xakjdxxb.2023.0613开放科学（资源服务）標识码（OSID）：

Ground deformation law of steel pipe jacking

construction in soft soils

LI Jiang

（China Railway 19th Bureau Group Rail Transit Engineering Co.，Ltd.，Beijing 101300，China）

Abstract：

In order to study the ground deformation law caused by steel pipe jacking construction in soft soil area，prediction formula，a water conveyance project in Dongguan was taken as the background，and numerical simulation and field monitoring methods were adopted to calculate and monitor the ground deformation caused by the jacking process，so as to obtain the vertical and horizontal ground deformation law during the jacking process.Firstly，the ground deformation prediction formula was deduced to consider the jacking clearance，and then the maximum vertical displacement 14.1 mm generated by pipe jacking construction was calculated.This deformation is within the allowable range of road settlement specification（≤20.0 mm），and there is no need to take measures such as soil reinforcement.Secondly，the finite element model was established by numerical simulation to calculate the ground deformation caused by the jacking，and the method to reduce the ground deformation was discussed.Lastly，the results from the above three methods were compared with those of field monitoring.The final results show that the shape of deformation curves obtained by the three methods is basically the same，except that the ground peak displacement at the pipe jacking axis（13.7 mm in numerical simulation and 15.2 mm in field monitoring）is slightly different.When the pipe jacking is carried out，the sedimentation tank of the transverse monitoring section is V-shaped，and the maximum settlement value is at the central axis of the pipe jacking.As the distance from the central axis increases，the settlement value decreases and eventually approaches 0.The longitudinal monitoring section shows an inverted “S” shape，which can be roughly divided into four stages：uplift of soil before jacking，settlement of soil in jacking，slight uplift of soil after jacking and stability of soil after jacking.Before pipe jacking construction，how to get the ground deformation is very necessary.Combined with the results of prediction and simulation，the soil deformation is controlled by setting the top thrust，grouting pressure and necessary soil reinforcement.The prediction formula presented in this paper has the characteristics of clear concept and strong operability，has good applicability in soft soil areas and can be used in similar projects in the future.The research results in this paper can provide scientific reference for ground settlement prediction and deformation control induced by similar pipe jacking projects in soft soil areas.

Key words：steel pipe jacking construction；ground deformation；prediction formula；numerical simulation；field monitoring；jacking clearance

0 引 言

顶管法是穿越公路、铁路、江河等不便于明挖区域管道施工常用的一种方法，具有开挖面积小、对地面交通及周边建筑物影响小等显著特点［1-2］。顶进过程中对管体周围土体会产生扰动进而引起地面变形，过大的变形会影响地面交通或导致建筑物沉降。因此顶管施工前需对其可能导致的地面变形进行预测，并根据变形量值对周边环境的影响程度采取有针对性的举措如土体注浆加固等［1-2］，这也是保证地下工程安全高效施工的必要前提。目前，中外学者关于顶管施工引起地面变形的问题研究比较多，如Peck假定土体水分不流失且均匀连续，土体损失的体积和沉降槽大小则是一致的，进而提出了基于土体损失理论的Peck公式，其常作为施工前的参考预测公式［3］；Sagaseta［4］进一步假定土体损失体积为圆柱体并进行同量径向移动，提出了Sagaseta公式来计算由土体损失引起的土体沉降值；魏纲利用Mindlin［8］公式推导修正了由顶管顶推力和摩阻力引起的地面变形公式，来进一步研究顶管施工过程中引起的地面沉降问题［5-7］;许有俊运用Mindlin弹性理论、随机介质理论、分层总和法分别对顶管施工中土体应力变化状态、地层损失、注浆填充和失水固结等方面进行了较为详尽的理论计算［9］；唐智伟等推导了由注浆引起的地面变形公式，并通过FLAC3D模拟了注浆引起的地面沉降［10］；张艳林等通过FLAC3D建立三维模型来模拟施工过程地表沉降规律，并与监测数据进行了对比［11］。前述研究为探究顶管施工引起的地表变形提供了良好的理论基础和研究方法，但也都有显著的不足，如计算理论过于繁杂不便于实施、计算方法经验系数过多以致缺乏可操作性等［12-23］。因此有必要提出一种概念清晰、计算简便的方法对钢顶管施工可能产生的地面变形进行预测。以广东东莞某自来水厂钢顶管施工的引水工程为背景，在先期采用考虑顶进间隙的地表变形预测公式对施工中可能引起的土体变形进行预测后，和后期数值模拟、现场监测的结果进行对比，研究分析其沉降规律并提出减轻地面变形的有效方法，以期为后续类似工程提供合理的参考。

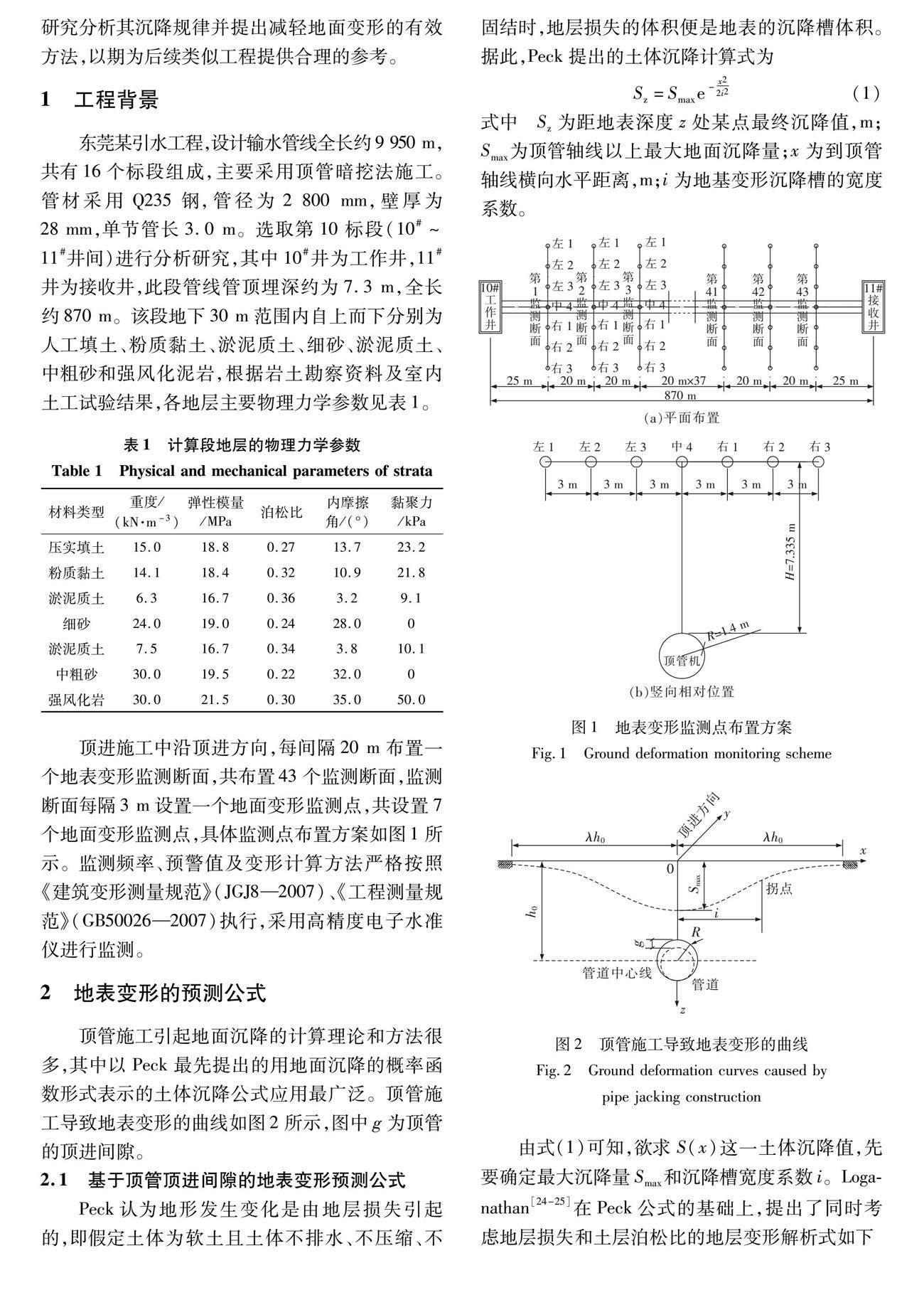
1 工程背景

东莞某引水工程，设计输水管线全长约9 950 m，

共有16个标段组成，主要采用顶管暗挖法施工。管材采用Q235钢，管径为2 800 mm，壁厚为28 mm，单节管长3.0 m。选取第10标段（10#～11#井间）进行分析研究，其中10#井为工作井，11#井为接收井，此段管线管顶埋深约为7.3 m，全长约870 m。该段地下30 m范围内自上而下分别为人工填土、粉质黏土、淤泥质土、细砂、淤泥质土、中粗砂和强风化泥岩，根据岩土勘察资料及室内土工试验结果，各地层主要物理力學参数见表1。

3 地表变形的数值计算

3.1 主要假定数值计算时主要考虑以下假定：

1）不考虑施工前的土体变形；2）不考虑土体沉降的时间效应；

3）土层均匀分布，且同一土层参数相同，土体不发生固结，注浆只作为润滑填充但不考虑其对土体的加固作用；4）顶推力均匀分布于开挖单元面；

5）顶进时土仓压力和注浆压力保持恒定。

3.2 计算模型为最大限度减少边界对管道及临近建筑的影响，综合考虑街道及房屋宽度等环境因素后，确定模型尺寸为80 m×60 m×30 m（长（X）×宽（Y）×高（Z）），其中宽（Y）的正方向为模拟顶进方向。在选取材料单元属性时，土层、注浆层采用理想弹塑性实体单元，摩尔-库伦屈服准则；管段及建筑物楼板采用弹性板单元；建筑物的梁柱采用弹性梁单元。

3.3 计算参数与边界条件

计算段地层的物理力学参数见表1，管段、注浆层和地表建筑物的计算参数见表3。顶进过程中，掌子面承受0.08 MPa的水土压力，管片周围承受0.10 MPa的注浆压力。

计算模型四周表面施加法向位移约束，底部施加固定边界，地表和掌子面为自由边界。根据以上条件建立了如图4所示的MIDAS/GTS数值计算模型。

3.4 计算结果

3.4.1 土体横向变形图5所示为第30监测断面数值模拟计算到的顶进不同距离后的地表横向变形。

从图5可以看出，地面土体横向沉降呈“V”形，顶管轴线正上方沉降量最大，向两边逐渐减小并最终趋于0；顶管机顶进过程中，工作面上方地表产生竖向沉降，最大沉降量为7.4 mm；随着向前逐渐推进，土体沉降量开始增大，在工作面后方3 m处沉降量为10.1 mm；在工作面后方6 m处沉降量达到12.6 mm，这是因为管节与顶管机存在直径差，虽及时注浆填补，且钝化了顶推力，但沉降值仍发生突变，使得沉降量快速增大；在工作面后方9，12，15 m处，沉降值分别为13.1，13.3，13.7 mm，沉降值增量逐渐减小，并趋于稳定，土体横向影响范围约为管径长度大小的3倍。

3.4.2 土体纵向变形图6所示为第30监测断面数值模拟计算得到的顶管中心轴线处纵向沉降。

图6中，“0”点表示顶管机头所在的位置，刻度表示钢顶管机距监测断面的距离，横坐标正方向为钢顶管开挖面的前方，负方向为钢顶管开挖面的后方；纵坐标正方向为土体隆起值，负方向为土体沉降值。从图6可以看出，顶进过程中，地面土体纵向呈倒“S”形，顶管顶进时的土体变形大致可分为以下4个阶段。第1阶段，顶进前土体的隆起。这一阶段发生在0～15 m处，监测断面最大隆起值在5.0 m处达到最大，约为3.2 mm；随着顶进距离的增大，地面隆起值逐渐减小，最终趋于零。这是由于顶管机机头的正面顶推力大于前方土体的被动土压力，使得前方土体受到挤压变形。第2阶段，顶进中土体的沉降。这一阶段发生在-5～0 m处，监测断面最大沉降值发生在-3 m处，原因为顶管机在顶进过程中对周围土体产生了扰动；顶管机直径略大于顶管，使顶管与土体之间产生空隙，从而导致土体产生沉降。第3阶段，顶进后土体轻微回隆。这一阶段发生在-6～-3 m处。原因是顶管施工过程中的同步注浆，

对顶管周围土体产生了挤压，因此在该阶段会产生土体沉降后的轻微回隆。第4阶段，顶进后土体稳定。这一阶段也是最主要的阶段，发生在-15～-6 m处。原因为顶管机对土体的扰动越来越小，且浆液与土体开始固结和二次固结，使得土体产生轻微沉降并开始趋于稳定。

3.4.3 临近建筑物变形

顶管上部道路宽约20 m，两侧存在6层的框架结构建筑物。顶管地表中心距北侧建筑物最近距离约7 m，在沉降槽宽度（约10 m）范围内，因此对建筑物有一定影响；其南侧建筑物最近距离约13 m，不在沉降槽宽度范围内，因此对其影响可忽略不计。图7为顶管施工完成后北侧建筑物变形云图。

建筑物远离施工轴线的一侧颜色为红色，几乎无沉降；靠近轴线的一侧为蓝色，沉降量较大，建筑物整体向顶管施工侧发生倾斜，图7所示该建筑物的最大沉降量为5.4 mm，远小于建筑物的允许最大沉降量（建筑物高度的1/1 000）。因此顶进施工不会对建筑物造成较大影响。

3.5 影响地表变形的主要因素

3.5.1 顶推力为分析顶推力对地表变形的影响，在原模型的基础上仅改变顶推力数值的大小，以原顶推力P为基准，分别改用1.0P、1.5P、2.0P进行数值计算，得到不同顶推力作用下地表横向变形图，如图8所示。从图8可以看出，2倍顶推力时地面最大沉降值为19.8 mm，1.5倍顶推力时地面最大沉降值为15.9 mm，分别是原顶推力作用下土体变形13.7 mm的1.44倍、1.16倍。据此看出，顶推力增大，可以加快顶进速度，但也会使得土体沉降量增加；反之，顶推力减小，土体沉降值减小，但会导致施工速度减缓，影响施工效率，进而影响工期。

3.5.2 注浆压力为分析注浆压力对土体变形的影响，在原数值模型的基础上改变注浆压力数值的大小，以实际注浆压力P0=0.1 MPa为基准，分别用P0、3P0、5P0的注浆压力进行模拟计算，得到不同注浆压力作用下地表横向变形图，如图9所示。

从图9可以看出，0.1，0.3，0.5 MPa时地面最大沉降值分别为13.7，13.0，12.7 mm，变化量分别为0.7，0.3 mm，这表明随着注浆压力逐渐增大，土体沉降值绝对值及变化量均在逐渐减小，也即当注浆压力达到一定数值时，继续增大注浆压力对土体最终沉降值不会再产生影响。顶管工程中，注浆压力过小会导致浆液密实度不够，最终使土体沉降量增加；注浆压力过大，虽可减小土体沉降，但也会对周围土体产生较大影响甚至会出现爆浆现象。因此合理地选择注浆压力对顶管施工具有十分重要的意义。

3.5.3 土体弹性模量

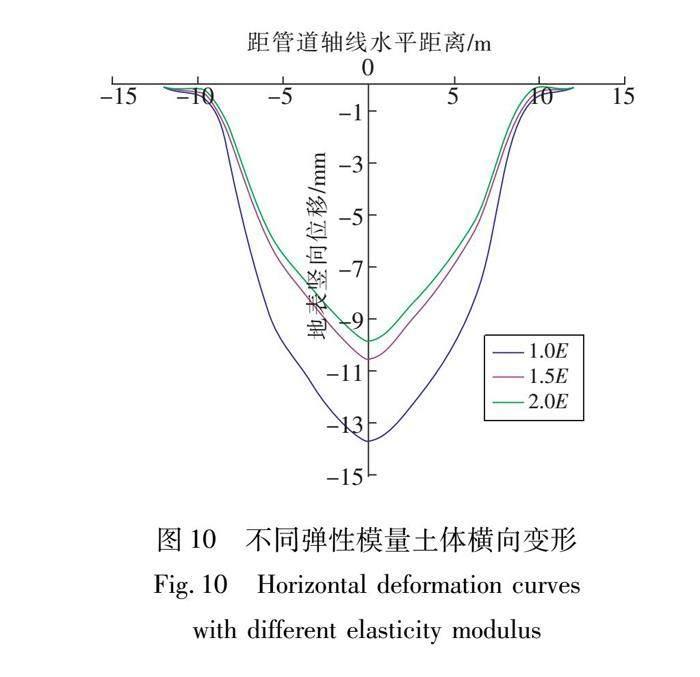
对可能产生过大变形的区域，顶管施工前需要对土体进行必要的注浆加固，也即改变了地层的弹性模量。在原模型的基础上改变弹性模量数值的大小，以土层原始弹性模量E为参考值，分别用1.0E、1.5E、2.0E进行计算，得到不同弹性模量下地表的横向变形图，如图10所示。

从图10可以看出，土体弹性模量增大到原值的1.5倍、2.0倍以后，地表竖向位移分别为10.5，9.8 mm，相当于原竖向位移13.7 mm的77%和72%，呈非线性变化，由此可知土体已经进入了塑性状态。顶管工程中，土体弹性模量对地表的最终变形影响很大。具体工程需根据不同的土质条件选择合理的施工方案，尤其是软土地区，土体弹性模量很小，抵抗变形能力较弱，对此种地层需采取必要的土体加固措施后方可施工，这样才能有效降低顶管施工对地表变形产生的不利影响。

4 地表变形的监测结果及对比分析

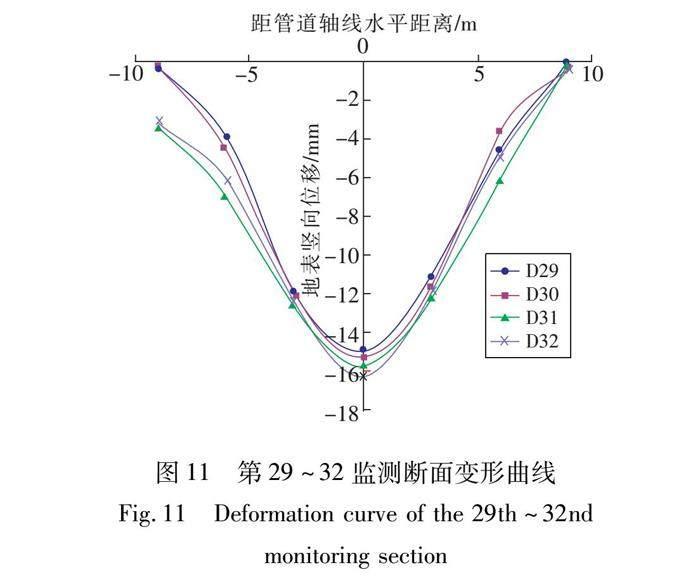
4.1 监测结果选取第29、30、31、32监测断面的监测数据绘制横向地表变形曲线，如图11所示。

从图11可以看出，监测断面折线图呈“V”型且相互交错，整体变化趋势基本相同；最大沉降量均发生在顶管轴线正上方，且随着两侧远离顶管中心，沉降变化量逐渐减小，沉降速率由快变缓。第29、30监测断面左侧9m处的位移量明显小于第31、32监测断面的数值，这是由顶管轴线左侧为道路主干道，施工期间有车辆等地面交通荷载所导致。

4.2 对比分析顶管施工对地面产生的不利影响主要集中在横向监测断面，为检验前述提出的地表变形预测公式及数值模拟的可靠性，以现场监测的第30断面竖向位移为基础，将3种方法所得的结果进行对比分析，得到如圖12所示的顶管轴线的横向地表变形结果对比。

从图12可以看出，预测公式、数值模拟及现场监测的土体变形整体变化规律基本一致，图形大致呈“V”形；在影响范围上，预测公式的变形范围约为5倍管径，大于数值模拟及现场监测的3倍管径；在最大沉降量方面，预测公式、数值模拟所得的14.1，13.7 mm与现场监测的15.2 mm相比，误差较小，且监测数据15.2 mm略大于理论计算与数值模拟数据，但也不超过20.0 mm，在工程允许的变形范围之内。总体来看，所提出的基于顶进间隙的预测公式具有概念清晰、可操作性强的特点，可以较好地对软土地区顶进施工产生的土体变形进行预测，但该公式未能考虑到地面的荷载作用，其预测结果可能会偏小；数值模拟的方法能有助于考虑地层因素和顶进过程中的顶推力、注浆压力等参数，可以更精确地模拟顶进施工全过程的地表及周边建筑物的变形，且能根据需要选择合适的监测断面进行分析，效果较好，但其前期建模和计算需要较好的理论基础。因此预测公式与数值模拟在顶管施工中均具有较高的参考价值，在实际施工过程中，可以根据需要选择相对合适的方式。整个引水工程的顶管施工已完成并投入使

用，现场监测结果表明地面沉降在允许的范围内。

5 结 论

1）基于顶进间隙的预测公式得到的数据与现场监测得到的地表横向变形结果基本相符，可以较好地反映地表变形规律，且所需参数少，可为后续类似工程参考。

2）顶管顶进时，横向监测断面的沉降槽成“V”形，最大沉降值在顶管中心轴线处，随着距离中心轴线越远，沉降值越小，最后趋于0。

3）顶管顶进时，地表纵向变形大致可分为顶进前的隆起、顶进中的土体沉降、顶进后的土体轻微回隆和顶进后的土体稳定4个阶段。

4）顶管法施工过程中，合理的顶推力、注浆压力和必要的土体补强可有效控制地表的变形。

参考文献（References）：

［1］ 余彬泉，陈传灿．顶管施工技术［M］.北京：人民交通出版社，1998.

［2］葛春辉．顶管工程设计与施工［M］．北京：中国建筑工业出版社，2012．

［3］PECK R B.Deep excavations and tunneling in soft g-round［C］//

Proceedings of the

7th International Conference on Soil Mechanics and Foundation Engineering，Mexico：

Balkema A A，1969：225-290.［4］

SAGASETA C.Analysis of undrained soil deformation due to ground loss［J］.Gotechnique，1987，37（3）：301-320.［5］魏纲，陈春来，余剑英.顶管施工引起土体垂直变形计算方法研究［J］.岩土力学，2007，28（3）：619-624.WEI Gang，CHEN Chunlai，YU Jianying.Study on calculating methods of soil vertical deformation induced by pipe jacking construction［J］.Rock and Soil Mechanics，2007，28（3）：619-624.［6］

魏纲，黄志义，徐日庆，等.顶管施工引起地面变形的计算方法研究［J］.岩石力学与工程学报，2005，24（S2）：5808-5815.WEI Gang，HUANG Zhiyi，XU Riqing，et al.Study on calculation methods of ground deformation induced by pipe jacking construction［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（S2）：5808-5815.［7］

魏纲，张鑫海，徐银锋.考虑多因素的类矩形盾构施工引起土体竖向位移研究［J］.岩石力学与工程学报，2018，37（1）：199-208.WEI Gang，ZHANG Xinhai，XU Yinfeng.Deriving vertical displacement of ground due to quasi-rectangular shield tunneling considering multiple factors［J］.Chinese Journal of Rock Mechanics and Engineering，2018，37（1）：199-208.［8］

MINDLIN R D.Force at a point in the interior of a semi-infinite solid［J］.

Physics，1936，7（5）：195-201.［9］

许有俊，史明，李育发，等.大断面土压平衡矩形顶管施工引起地表竖向变形研究［J］.武汉大学学报（工学版），2020，53（7）：597-604.XU Youjun，SHI Ming，LI Yufa，et al.Study on vertical deformation of ground caused by construction of large section soil pressure balanced rectangular pipe jacking［J］.Engineering Journal of Wuhan University，2020，53（7）：597-604.［10］

唐智偉，赵成刚．注浆抬升地层的机制、解析解及数值模拟分析［J］.岩土力学，2008，29（6）：1512-1516.TANG Zhiwei，ZHAO Chenggang.Mechanisms of ground heave by grouting and analytical solutions & numerical modeling［J］.Rock and Soil Mechanics，2008，29（6）：1512-1516.［11］

张艳林，曾天成，甘甜，等． 真实复杂地层大直径钢顶管三维数值模拟研究［J］.科学技术与工程，2020，20（33）：13791-13798.ZHANG Yanlin，ZENG Tiancheng，GAN Tian，et al.Three-dimensional numerical simulation of large-diameter steel pipe jacking in real and complex strata［J］.Science Technology and Engineering，2020，20（33）：13791-13798.［12］

吴修锋.顶管施工引起的地层移动与变形控制研究［D］．南京：南京工业大学，2004.WU Xiufeng.Study on strata movement and deformation control caused by pipe jacking construction［D］.Nanjing：Nanjing Technology University，2004.［13］房营光，莫海鸿，张传英．顶管施工扰动区土体变形的理论与实测分析［J］．岩石力学与工程学报，2003，22（4）：601-605．FANG Yinguang，MO Haihong，ZHANG Chuanying.Theoretic and testing analysis of soil deformation in the area of disturbance caused by pipe-jacking［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（4）：601-605.［14］

方从启，王承德.顶管施工中的地面沉降及其估算［J］.江苏理工大学学报，1998，19（4）：106-110．FANG Congqi，WANG Chengde.Ground subsidence andits estimation in pipe jacking construction［J］.Journal of Jiangsu University of Science and Technology，1998，19（4）：106-110.［15］

韩煊，李宁.隧道施工引起地层位移预测模型的对比分析［J］.岩石力学与工程学报，2007，26（3）：594-600.HAN Xuan，LI Ning.Comparative analysis of strata prediction models for ground movement induced by tunnel construction［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（3）：594-600.［16］

阳军生，刘宝琛.城市隧道施工引起的地表移动及变形［M］.北京：中国铁道出版社，2001.［17］

黄宏伟，胡昕.顶管施工力学效应的数值模拟分析［J］.岩石力学与工程学报，2003，22（3）：400-406．HUANG Hongwei，HU Xin.3D numerical analysis on construction mechanics effect of pipe jacking［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（3）：400-406.［18］

施成华，彭立敏.随机介质理论在盾构法隧道纵向地表沉降预测中的应用［J］．岩土力学，2004，25（2）：320-323．SHI Chenghua，PENG Limin.Application of stochastic medium theory to predicting settlement in longitudinal ground due to tunnel construction by shield［J］.Rock and Soil Mechanics，2004，25（2）：320-323.［19］杨建华.饱和软黄土地层地铁隧道施工诱发的地表变形［J］.西安科技大学学报，2018，38（1）：91-98.YANG Jianhua.Ground deformation induced by tunnel construction in saturated soft loess strata［J］.Journal of Xian University of Science and Technology，2018，38（1）：91-98.［20］赖金星，王开运，侯丹丹，等.砂土地层顶管施工土体变形规律三维数值分析［J］.西安科技大学学报，2015，35（4）：450-457.LAI Jinxing，WANG Kaiyun，Hou Dandan，et al.3D numerical analysis on displacement regularity of pipe jacking sewer in sand soil stratum［J］.Journal of Xian University of Science and Technology，2015，35（4）：450-457.［21］

LI Y，EMERIAULT F，KASTNER R，et al.Stability analysis of large slurry shield-driven tunnel in soft clay［J］.Tunneling and Underground Space Technology，2009，24（4）：472-481.［22］ZHOU S，LI X，JI C，et al.Back-fill grout experimental test for discharged soils reuse of the large diameter size slurry shield tunnel［J］.KSCE Journal of Civil Engineering，2017，21（3）：1-9.［23］

HELMUT F.SCHWEIGER，KUMMERER C.Numerical modeling of settlement compensation by means of fracture grouting［J］.Soils and Foundations，2004，44（1）：71-86.［24］LOGANATHAN N，POULOS H G.Analytical prediction for tunneling-induced ground movement in clays［J］.Journal of Geotechnical and Geoenvironmental Engineering，1998，124（9）：846-856.［25］

ATTEWELL P B，FARMER I W.Ground settlement above shield driven tunnels in clay［J］.Tunnels and Tunneling，1975，7（1）：58-62.［26］

高丙麗，蔡智云，王金华，等.黄土地区地铁隧道地层变形规律［J］.西安科技大学学报，2015，35（3）：331-335.GAO Bingli，CAI Zhiyun，WANG Jinhua，et al.Strata deformation laws of the pipeline caused by the subway tunnel in loess area［J］.Journal of Xian University of Science and Technology，2015，35（3）：331-335.［27］

吴昌胜，朱志铎.不同直径盾构隧道地层损失率的对比研究［J］.岩土工程学报，2018，40（12）：2257-2265.WU Changsheng，ZHU Zhiduo.Comparative study on ground loss ratio due to shield tunnel with different diameters［J］.Chinese Journal of Geotechnical Engineering，2018，40（12）：2257-2265.［28］

郑馨，麻凤海.长春地层地铁隧道施工的Peck公式改进［J］.地下空间与工程学报，2017，13（3）：732-736.

ZHENG Xin，MA Fenghai.Improvement of peck formula in subway construction in Changchun［J］.Chinese Journal of Underground Space and Engineering，2017，13（3）：732-736.［29］馬险峰，王俊淞，李削云，等.盾构隧道引起地层损失和地表沉降的离心模型试验研究［J］.岩土工程学报，2012，34（5）：942-947.MA Xianfeng，WANG Junsong，LI Xiaoyun，et al.Centrifuge modeling of ground loss and settlement caused by shield tunneling in soft ground［J］.Chinese Journal of Geotechnical Engineering，2012，34（5）：942-947.

［30］

李国成，丁烈云.武汉长江隧道盾构施工引起的地表沉降预测［J］.铁道工程学报，2008，25（5）：59-62.LI Guocheng，DING Lieyun.Ground settlement induced by shield construction of Wuhan Yangtze River Tunnel［J］.Journal of Railway Engineering Society，2008，25（5）：59-62.

（责任编辑：高佳）