基于牵引制动性能的轮轨接触行为研究

牟明慧，赵龙志，陈道云

（1.华东交通大学交通运输工程学院，江西 南昌 330013；2.华东交通大学网络信息中心，江西 南昌 330013；3.华东交通大学材料科学与工程学院，江西 南昌 330013；4.华东交通大学轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013）

轮轨关系是动车组九大关系之首，轮轨间的接触力学行为直接影响轮轨匹配关系，正确揭示轮轨间的接触力学行为对于保障列车安全运行意义重大[1-7]。在列车轴重保持恒定的情况下，轮轨摩擦系数将直接影响轮轨接触的力学行为，因此合理的轮轨摩擦系数模型成为研究轮轨接触力学行为的关键。

朱文良[8]针对轨道车辆制动工况下的低黏着特性分析了防滑控制作用下制动力调节引起轮轨间黏着变化和改善的原因，基于滑动功率和滑动能对Polach 黏着模型进行了改进,给出了适用于制动工况下的轮轨低黏着模型。师陆冰[9]研究了不同工况下的轮轨黏着-蠕滑曲线特性，结果表明水、油工况导致摩擦系数明显降低，撒砂可有效提高摩擦系数。赵小罡[10]分析了轮轨滚滑作用下裂纹面之间的瞬态法、切向接触和裂尖动态应力场强度因子，结果表明滚滑状态下的轮轨法、切向接触力不随轮轨摩擦系数的增加而变化，但裂纹面间的最大法、切向接触力却随摩擦系数的增加而不断减小。焦琬晴[11]建立了一种轮轨界面存在水介质时的黏着特性三维数值模型，讨论了速度、表面粗糙度和边界摩擦系数对摩擦系数的影响，结果表明，温升情况下摩擦系数高于等温情况下摩擦系数，速度和表面粗糙度对摩擦系数影响较大且界面温升会使摩擦系数增加。胡雅婷[12]在不同介质工况下进行了轮轨横向黏着特性试验，结果表明在干态与水介质下横向摩擦系数随着速度的增大而降低，而在油介质下横向摩擦系数随着速度的增大而增大。Hua[13]基于双盘滚动试验机改进了轮轨摩擦系数的预测方法，发现摩擦系数随行驶速度增加而降低，最终结果与日本新干线车辆的试验结果保持了良好的一致性。Keropyan[14]对露天矿机车工作面与钢轨的相互作用条件进行了理论和实践研究，确定了合理的轮轨摩擦系数值，以缩短轮轨的磨合期。Shu[15]研究了动态风沙环境对不同滑移率下轮轨磨损和损伤行为的影响，结果表明在戈壁、沙漠和干旱三种条件下，摩擦系数随滑移率的变化趋势并不完全相同，随着滑移率的增加，轮轨的疲劳磨损逐渐加剧。吴萌岭[16]研究了水介质工况下制动过程的轮轨摩擦系数动态变化规律，发现摩擦系数随着滑移率增大呈现先上升后饱和下降再上升的趋势。

可见，研究者从服役工况、轮轨接触介质等角度以仿真和试验的方式研究了轮轨摩擦系数的动态变化，但是当前动车组轮轨摩擦系数模型多采用经验模型[17-19]，该模型将列车运行速度纳入摩擦系数的影响因素中，虽适用性广但缺乏严格的科学依据，未突出不同车型的摩擦系数差异。本文在轮轨间黏着力提供列车牵引力与制动力的基本事实基础上，建立了CRH2-300 列车牵引及制动性能摩擦系数模型，同时以轮轨摩擦系数的经验模型作为参照，通过三维轮轨接触有限元仿真模拟了启动和制动工况下的轮轨滚滑接触力学行为，分析了两种摩擦系数模型间的异同。

1 轮轨摩擦系数模型

轮轨间的摩擦系数直接影响列车的牵引力与制动力水平，我国当前普遍采用的轮轨摩擦系数模型是基于以往测试积累的经验得到的，具体公式如下[20]

式中：v 为列车运行速度。

事实上，轮轨间的摩擦系数会随着牵引力、牵引黏着质量、制动力、制动黏着质量等参数的不同而改变，基于列车牵引与制动过程的基本事实，构造轮轨牵引摩擦系数μT和制动摩擦系数μB如下

式中：F 为牵引力；MT为牵引黏着质量；g 为重力加速度。

式中：B 为制动力；MB为制动黏着质量。

本文以CRH2-300 型动车组为研究对象，其牵引与制动性能的具体参数如图1 所示，结合本文建立的牵引摩擦系数和制动摩擦系数模型可求解出轮轨摩擦系数值，将计算结果与经验模型及日本新干线模型进行对比，如图2 和图3 所示，可见，基于经验模型的摩擦系数显著大于基于牵引、制动模型的摩擦系数及新干线模型的摩擦系数，新干线模型的摩擦系数与基于牵引制动性能模型的摩擦系数较为接近。

图1 CRH2-300 列车牵引与制动性能参数Fig.1 Traction and braking performance parameters of CRH2-300

图2 牵引工况下的摩擦系数Fig.2 Friction coefficient under traction condition

图3 制动工况下的摩擦系数Fig.3 Friction coefficient under braking conditions

2 轮轨接触有限元模型

2.1 模型基本参数及计算工况设置

轮轨接触有限元模型基于CRH2-300 型动车组轮轨参数建立，由8 节点六面体单元离散。在模型的求解区，接触属性设置为基于罚函数法的“面-面”接触，为尽可能减少模型的计算规模而又不损失解的精度，划分轮轨时采用不均匀网格。接触带处最细密（单元尺寸约为1 mm），用以求解轮轨接触，越远离接触带，网格越粗大。考虑到轮轨瞬态接触是与时间相关的非线性问题，网格划分采用Lagrangian描述，共离散为367 536 个单元和445 126 个节点。轮轨接触模型考虑弹性滑动，表面特征尺寸百分比设定为建议值0.005。最终得到的轮轨接触有限元模型如图4 所示。

图4 轮轨三维有限元模型Fig.4 The wheel-rail 3D finite element model

在启动牵引工况下，为了建立稳定收敛的计算模型，在ABAQUS 中建立了3 个分析步，其中第1分析步为初始分析步，第2 分析步为静态接触分析步，第3 分析步为动态隐式分析步，第2 和第3 分析步时间分别定为1 s 和2 s，同时激活几何非线性属性。在制动工况下，建立了4 个分析步，其中第1分析步为初始分析步，第2 分析步为静态接触分析步，共1 s 时长，第3 分析步为动态隐式分析步对车轮进行加速，共0.1 s 时长，第4 分析步为动态隐式分析步对车轮实施制动减速，共0.07 s 时长。

在计算工况中，轮轨材料属性均设置为线弹性材料，其中车轮材料为ER8，弹性模量为206 000 MPa，泊松比为0.3；钢轨材料为PD3，弹性模量为184 000 MPa，泊松比为0.3。在静态载荷步和动态载荷步中，钢轨底部均定义为全约束；在静态载荷步中，车轮只有竖直方向的约束被放开，而在动态载荷步中，车轮垂向、纵向及转动轴旋转方向的约束均被放开。采用罚函数法定义轮轨接触面间的切向力行为，其中，方向性为各向同性，摩擦系数基于牵引及制动性能计算出的摩擦系数值而定义，轮轨法向压力过盈设置为“硬”接触，约束执行方法为罚函数，允许接触后分离，接触刚度定义为线性，刚度比例因子为1，不考虑轨面不平顺。

在静态接触分析步中，为了模拟CRH2-300 型动车组在定员工况下的轴重，将轴重换算为载荷施加到车轮中心耦合点处，数值为51 450 N，方向为y轴负方向（竖直向下）；在动态隐式分析步的计算中，根据CRH2-300 型动车组的启动和制动性能参数，将车轮的启动加速度和制动加速度（常用制动）数值分别设定为0.48 m/s2和0.75 m/s2，启动加速度和制动加速度的施加位置均位于车轮旋转中心的耦合点，其中启动加速度方向沿z 轴正方向，制动加速度方向沿z 轴负方向。

2.2 有限元模型准确性验证

以下通过轮轨接触应力的经典公式计算出轮轨最大接触应力，将得到的解析解与静态接触仿真的结果进行对比，验证所建立模型的准确性。

参考谢红太[21]的计算结果，CRH2-300 型动车组轮轨接触的接触区域长半轴和短半轴数值解分别为a=7.517 mm 和b=4.695 mm，轴重载荷为51 450 N，根据式（4）可计算得到轮轨最大接触应力的解析解为696.4 MPa。

式中：P 为轴重分配于车轮的载荷；a 为接触区椭圆长半轴；b 为接触区椭圆短半轴。

单独对轮轨静态接触工况进行计算，分析轮轨接触斑的最大接触应力及接触椭圆长半轴和短半轴长度（如图5 所示），将仿真计算结果与公式计算的解析解进行对比，如表1 所示。可见，公式计算的解析解与仿真解在最大接触应力、接触椭圆长半轴长度和短半轴长度等方面的相对误差较小，均不超过4%，证明所建立的论文模型具有较好的准确性，可进一步进行后续的分析。

图5 轮轨静态接触应力状态Fig.5 Stress state of wheel-rail static contact

表1 解析解与仿真解对比分析Tab.1 Comparison between analytical solution and simulation solution

3 有限元仿真结果分析

3.1 接触面力学参数

3.1.1 接触面法向及切向力

图6 及图7 所示分别为牵引和制动工况下的轮轨接触面法向力动态变化，由图可见，在牵引工况下，轮轨接触面法向力在列车刚启动的0.25 s 内呈现迅速衰减的特征，这是因为在牵引工况前施加了1 s 时长的静态接触力工况，存在较大的接触振动，当进入牵引工况后，轮轨间的法向接触得到了持续衰减，而制动工况下的前一分析步是加速工况，因此静态接触力已经过有效衰减，因此不存在制动开始阶段的力衰减情况。随后，两种工况下的接触面法向力在较小振幅内围绕10 kN 左右的均值呈现稳定的振动形态，基于经验模型和牵引制动性能模型的接触面法向力振动均值基本保持一致，这表明不同模型造成的摩擦系数改变未对轮轨接触面法向力造成显著影响。进一步观察牵引及制动过程中4 个时刻下的接触面法向力云图，发现不同时刻牵引和制动工况下的云图形貌基本一致，为单点接触且接触区椭圆形由中心向外放射。

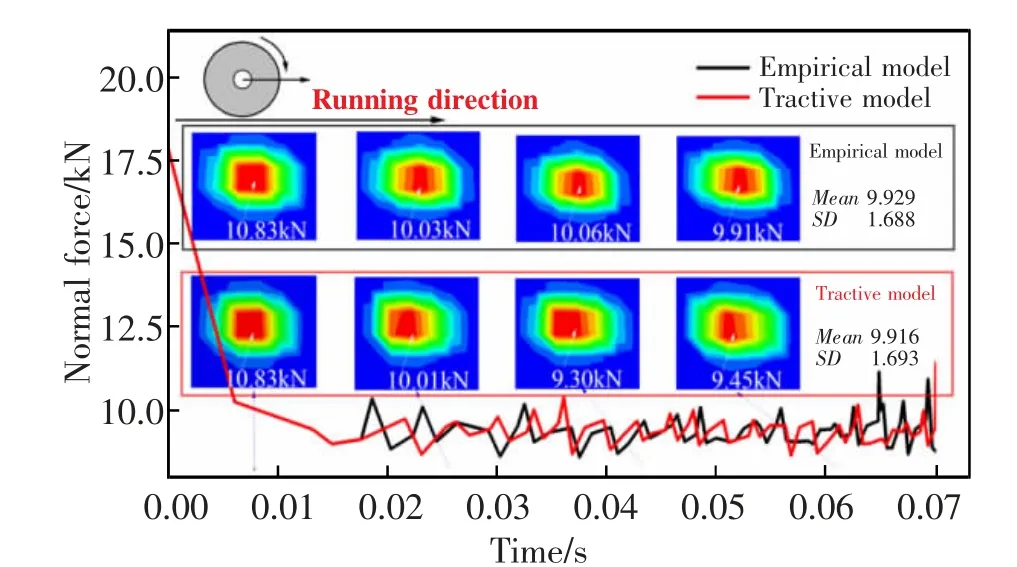
图6 牵引工况下的轮轨接触面法向力动态变化图Fig.6 Dynamic variation diagram of normal force on wheel-rail contact surface under traction condition

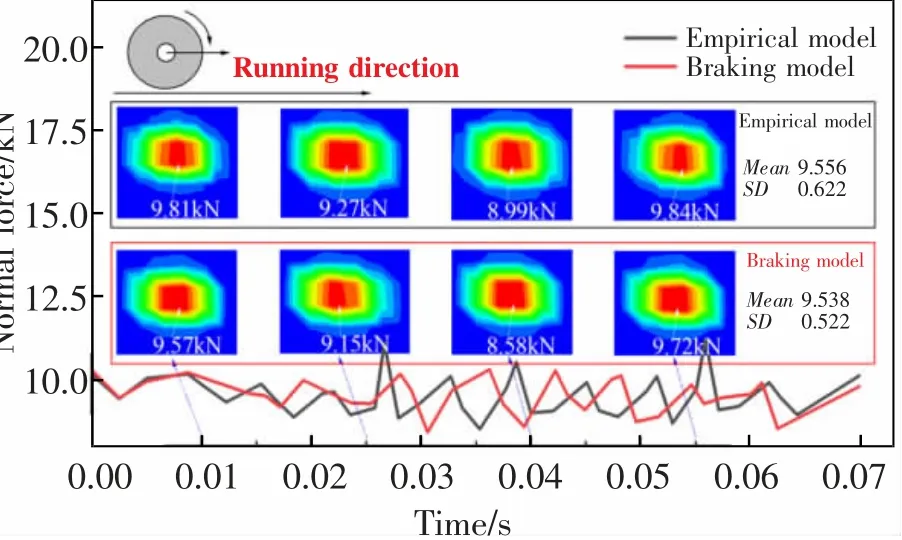
图7 制动工况下的轮轨接触面法向力动态变化图Fig.7 Dynamic variation diagram of normal force on wheel rail contact surface under braking condition

由于考虑计算时间成本的原因，模型在静态及动态接触计算的时长偏短。在静态载荷步中，轮轨接触的一瞬间将产生较大幅值的接触载荷振动，这种振动会随着时间的推移而逐渐减弱，由于后续动态分析步给定的时间较短，因此前述衰减振动没有完全消失，最终导致了接触力计算结果存在小幅波动。

通过分析图8 和图9 可知，在牵引和制动过程中的绝大部分时刻存在经验模型的接触面切向力大于牵引及制动模型接触面切向力的现象，其中，在牵引工况下，经验模型及牵引性能模型在起始时刻处的切向力达到最大值，随后便缓慢降低至0.3 kN左右的均值并小幅振动；在制动工况下，经验模型及制动性能模型在起始时刻处的切向力达到最大值且该最大值明显高于牵引工况下的最大值，随后切向力迅速衰减至0.5 kN 左右的均值并小幅振动，由此可见稳定振动后的制动工况切向力均值高于牵引工况切向力均值。进一步分析切向力云图可知，牵引工况下的经验模型和牵引性能模型切向力云图均呈现“两点”接触形态，且沿运行方向前端的点接触切向力明显大于运行方向后端的点接触切向力；在制动工况下，经验模型和制动性能模型的切向力在起始时刻呈现“单点”接触，此时轮轨接触面间处于全滑动状态，随后轮轨间呈现“两点”接触状态，轮轨间恢复黏着接触状态。

图8 牵引工况下的轮轨接触面切向力动态变化图Fig.8 Dynamic variation diagram of tangential force on wheel-rail contact surface under traction condition

图9 制动工况下的轮轨接触面切向力动态变化图Fig.9 Dynamic variation diagram of tangential force on wheel rail contact surface under braking condition

3.1.2 接触压力

当接触过程稳定后，轮轨间的接触压力保持稳定，其中，牵引工况下的经验模型与牵引性能模型接触压力水平基本一致，制动工况下的经验模型与制动性能模型接触压力水平基本一致。进一步分析可知，两种工况下经验模型与牵引制动性能模型的接触压力云图均呈现椭圆形，如图10 和图11 所示。

图10 牵引工况下的轮轨接触压力动态变化图Fig.10 Dynamic variation diagram of wheel-rail contact pressure under traction condition

图11 制动工况下的轮轨接触压力动态变化图Fig.11 Dynamic change diagram of wheel-rail contact pressure under braking condition

3.1.3 接触节点面积

在轮轨接触中，每个节点的接触面积由以下公式表示

式中：ncont-i为包含节点i 的潜在接触约束数量；cij为接触约束系数；Aj为约束j 的面积。

图12 所示为牵引工况下的轮轨节点接触面积动态变化图，可见在牵引过程中经验模型与牵引性能模型的节点接触面积呈现稳定的趋势，虽有波动但振幅较小且相对恒定，轮轨间始终保持接触，未出现分离。根据节点接触面积云图可知，牵引的起始时刻尚未施加转矩，接触面积云图呈现圆形分布，在施加转矩并开始转动后，接触面积云图呈现细长的椭圆形分布形态。

图12 牵引工况下的轮轨节点接触面积动态变化图Fig.12 Dynamic change diagram of wheel-rail node contact area under traction condition

根据图13 所示的制动工况下轮轨节点接触面积动态变化图可知，制动过程中的经验模型与牵引性能模型节点接触面积也呈现稳定的趋势，以小振幅波动，在制动全过程中的节点接触面积云图均呈现近似椭圆形分布，此外，在接触区域的横向可见小面积的节点接触。

图13 制动工况下的轮轨节点接触面积动态变化图Fig.13 Dynamic change diagram of wheel-rail node contact area under braking condition

3.2 轮轨内应力

3.2.1 VonMises 等效应力

图14 和图15 所示分别为轮轨在牵引和制动工况下的VonMises 等效应力动态变化图，可见在两种工况下，经验模型的等效应力变化趋势与牵引及制动模型的等效应力变化趋势保持一致，经验模型的等效应力极值在整体上略高于牵引及制动模型的等效应力。通过等效应力云图分析可以发现，同一时刻轮轨接触时的最大等效应力发生于轨道接触面以下的次表层，车轮本身的等效应力最大值位于踏面以下次表层。

图14 牵引工况下的轮轨Mises 应力动态变化图Fig.14 Dynamic variation diagram of wheel-rail Mises stress under traction condition

图15 制动工况下的轮轨Mises 应力动态变化图Fig.15 Dynamic variation diagram of wheel-rail Mises stress under braking condition

3.2.2 S23 切应力

在牵引和制动工况下，由经验模型及牵引制动模型计算的轮轨纵向剖面S23 切应力动态变化如图16 和图17 所示，由图可见，在两种计算工况下，不同摩擦系数模型计算的S23 切应力均值并未有明显差异，S23 切应力云图均呈现出类似的分布形态且钢轨在S23 正方向和负方向的切应力最大值均大于车轮，其中，在轮轨接触点处，车轮S23 切应力呈现圆弧状形态且圆弧走势与车轮角速度方向一致，钢轨S23 切应力也呈现圆弧状形态且圆弧走势与车轮S23 切应力圆弧走势对称；在轮轨接触点两侧，车轮和钢轨分别出现了与接触点位置处S23切应力正负方向相反的S23 切应力；在轮轨接触点远离运行方向的材料后侧区域，可见有正负交替出现的小幅值S23 切应力出现。

图16 牵引工况下轮轨S23 切应力动态变化图Fig.16 Dynamic variation diagram of wheel-rail S23 shear stress under traction condition

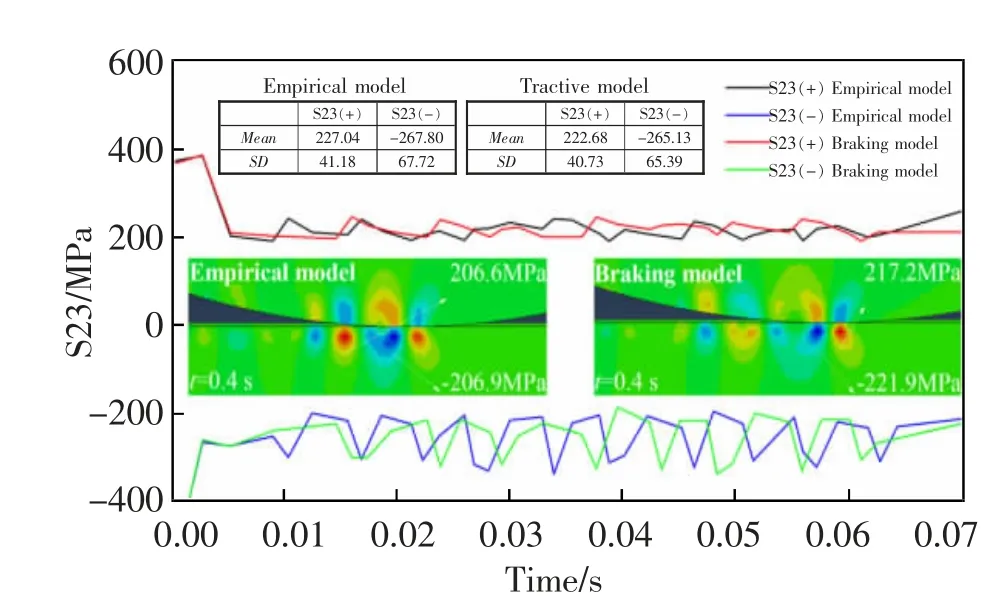
图17 制动工况下轮轨S23 切应力动态变化图Fig.17 Dynamic variation diagram of wheel-rail S23 shear stress under braking condition

4 结论

1）基于经验模型的摩擦系数显著大于基于牵引、制动模型的摩擦系数及新干线模型的摩擦系数，新干线模型的摩擦系数与基于牵引制动性能模型的摩擦系数较为接近。

2）经验模型的接触面切向力大于牵引及制动模型，在牵引工况下，经验模型及牵引性能模型在起始时刻处的切向力达到最大值，随后缓慢降至0.3 kN 左右的均值并小幅振动，而在制动工况下，经验模型及制动性能模型在起始时刻处的切向力最大值明显高于牵引工况，随后迅速衰减至0.5 kN左右的均值并小幅振动。

3）经验模型与牵引及制动模型的等效应力变化趋势保持一致，轮轨接触的最大等效应力位于接触面以下的次表层。钢轨在S23 正方向和负方向的切应力最大值均大于车轮，在轮轨接触点处，车轮S23 切应力呈圆弧形且圆弧走势与车轮角速度方向一致，钢轨与车轮S23 切应力圆弧走势对称。