翻滚非合作目标逼近与跟踪的轨道和姿态控制

夏 新，陈新龙

（中国空间技术研究院钱学森空间技术实验室，北京 100094）

0 引言

随着航天科技的不断发展，人们为了更好地探索和利用空间资源，越来越多结构复杂、功能多样的航天器被送入太空。许多航天器由于燃料耗尽、故障废弃、碰撞损坏甚至解体等原因，成为了空间碎片，挤压了可用的轨道资源，造成空间环境的不断恶化，对其他正常航天器的在轨安全运行和任务开展造成了影响[1-4]。

出于发展空间技术、提高航天器利用率、减少太空垃圾等目的，在轨服务已成为世界主要航天国家积极面对和解决的重要课题。交会对接技术是保证在轨维修、维护、组装、捕获航天器，清理空间碎片等多种在轨服务任务成功的关键技术之一。目前，合作式交会对接技术已经发展得较为成熟，以空间碎片等为任务目标的非合作式交会对接技术对航天器操作而言，更加复杂，成为了航天领域的研究热点之一。

包括失效航天器在内的空间碎片可能具有高动态特征，在引力等作用下发生旋转翻滚[5-6]。出于清理空间碎片的任务需求，须要与翻滚非合作目标完成交会对接，实现对目标的逼近与跟踪，为捕获清除创造稳定的操作条件，降低在轨操作过程中可能对服务航天器造成的冲击。因此，有必要对近距离逼近跟踪过程中的姿轨耦合控制进行研究。

关于航天器的姿轨耦合控制研究：高登巍等采用θ-D控制方法研究了航天器轨道和姿态联合控制问题[7]；徐帷提出了视线指向跟踪的控制方法，实现了相对轨道、姿态的联合控制[8]；张博翔在滑模控制基础上，利用预设性能控制方法设计了控制器[9]；Sun 和Huo考虑了模型不确定情况下的姿轨耦合控制[10]；Xia和Huo基于六自由度相对运动耦合模型，利用反步法和径向基神经网络设计了位姿控制策略[11-12]；武冠群等基于积分滑模控制理论设计了具有抗饱和特性的自适应控制器[13]；陶佳伟考虑执行机构的非线性饱和特性，设计了基于辅助饱和系统的姿轨耦合控制器[14]；黄艺针对航天器的近距离强迫绕飞问题设计了基于反步法的姿轨耦合控制器[15]。

目前这些研究主要针对于目标姿态稳定或者变化较为缓慢的情况，未能充分考虑空间碎片的高速旋转特性，有必要做进一步研究。受文献[16]中解决小卫星姿态镇定问题的启发，本文针对与翻滚非合作目标交会对接的轨道和姿态控制问题，在目标器体坐标系下建立了相对姿轨耦合运动模型；充分考虑工程实践中系统质量和惯量不能精确获知以及控制输入有限的问题，在存在参数不确定性，外部扰动以及控制输入受限的情况下，设计了鲁棒自适应位置和姿态控制器；基于李雅普诺夫稳定理论，严格证明了系统的稳定性；通过仿真结果验证了控制律的有效性。

1 动力学模型

1.1 位置运动模型

在惯性坐标系下，服务航天器、翻滚非合作目标（以下简称“目标器”）的动力学方程[17]分别表示为：

式（1）中：μ为引力常数；m为服务航天器的质量；rc和rt分别为服务航天器和目标器在惯性系下的位置；Fc为服务航天器的控制力；dc为服务航天器所受到的干扰力；ad为目标器在干扰下产生的干扰加速度。

令r=rc-rt，。记rb为目标器体坐标系下服务航天器相对于目标器的位置矢量，则有：其中，ωd为目标器体坐标系相对于惯性坐标系的相对角速度，也是服务航天器的期望角速度。由于目标不受主动控制作用，故可认为=0。分别将矢量f、dc-mad、Fc从惯性系下转换到目标器体坐标系下，记转换后的矢量分别为fb、db、Fb，则可得：

为建立稳定的相对位姿关系，假设服务航天器在目标器体坐标系下的期望最终位置坐标为常矢量rd，定义误差向量，则重写式，且考虑控制输入受限，可以得到相对位置运动模型为：

式（2）中：Fbi为Fb的分量；Fm1、Fm2、Fm3分别为服务航天器在目标器体坐标系三轴方向上的最大控制力大小；为饱和特性函数，下同。

1.2 姿态运动模型

考虑到在轨任务中可能会存在大角度姿态机动，采用四元数描述姿态，服务航天器的姿态运动学和动力学方程如下：

式（4）中：J=JT表示服务航天器的惯量矩阵；ω为服务航天器本体系相对惯性坐标系的角速度矢量；q和q0分别为服务航天器本体系相对惯性坐标系的姿态四元数的矢量部分和标量部分；u为服务航天器的控制力矩矢量；d为服务航天器受到的干扰力矩矢量。

令qe和qe0分别为姿态误差四元数的矢量部分和标量部分，ωe为误差角速度，有ωe=ω-Reωd。其中，Re为目标器本体系到服务航天器本体系的变换矩阵。记um1、um2、um3分别为服务航天器在服务航天器本体系三轴方向上的最大控制力矩大小，在控制输入受限约束下，相对姿态运动模型为：

2 鲁棒自适应控制器设计

2.1 位置控制器设计

假设不能获知质量参数的准确值，对控制力Fb进行设计，以使

采用滑模变结构控制[18]，定义滑模面：，其中，k为正常数。鲁棒自适应位置控制器如下：

本控制器的设计思想是在控制过程中，利用s不断修正、和，进而不断调整控制力，直至s收敛到一定精度范围内，保证系统稳定。

2.2 姿态控制器设计

在惯量矩阵不能被精确获知的情况下，采用同样的控制思想进行控制力矩u的设计，使得

定义滑模面：s=-ωe-kqe，其中，k为正常数。定义为误差调节角加速度，记：

系统姿态动力学方程可以改写为：

3 稳定性分析

引理1[16]定义正定函数V(t)，假设V(t)满足，λ为正常数，Φ(t)>0,∀t>0。若Φ(t)=C为一正常数，则系统是全局一致最终有界稳定的，且对∀t>0 有：

3.1 位置控制系统的稳定性证明

故如果有：

及

则∀t>0 ，<0 成立。

通过在控制过程中适当选取参数ςi( 0 )、εi、，可以保证式成立，系统渐进稳定。参数选取方式见情况1。在控制过程中，可近似认为用σ1、σ2、σ3设定了边界层，在σ1、σ2、σ3过小的情况下，如果系统出现超调，可能导致情况1与情况2来回切换频繁，出现小幅等幅振荡。一旦遇到这种情况，可以通过适当增加σ1、σ2、σ3的值来改善控制效果。

情况3：当 |si|≤σi(i=1,2,3) 时，由式（26）有：

3.2 姿态控制系统的稳定性证明

构造Lyapunov函数：

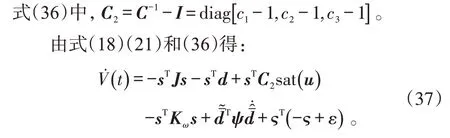
易知，其分类讨论分析情况与位置控制稳定性证明中的分析过程类似，以下只说明主要结论。

当 情 况1 为 |si|>σi(i=1,2,3) 或 者 情 况2 为|s1|、|s2|、|s3|与其对应的σ1、σ2、σ3的3 对大小关系不完全一致时，通过在控制过程中适当选取参数ςi( 0 )、，可以保证系统渐进稳定。当情况3 为|si|≤σi(i=1,2,3) 时，系统全局一致最终有界稳定。

4 仿真

4.1 仿真参数

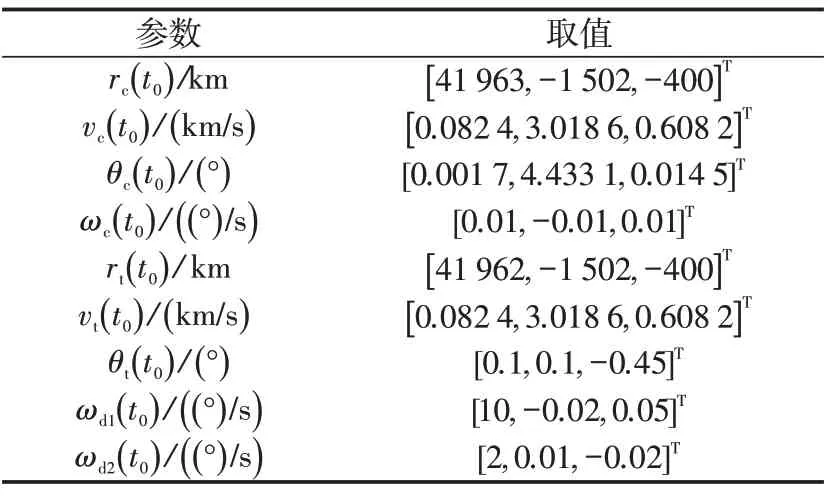
表1 仿真参数Tab.1 Simulation parameters

为了验证在“目标姿态变化很快”以及“较为缓慢”2种不同情形下，服务航天器在本控制器的作用下是否都能完成与目标器的交会对接，设定2 个不同的目标器初始姿态角速度为ωd1和ωd2。

位置控制器参数：

姿态控制器参数：

4.2 仿真结果

情况1：目标器以ωd1的姿态角速度高速旋转，仿真结果如图1～4所示。

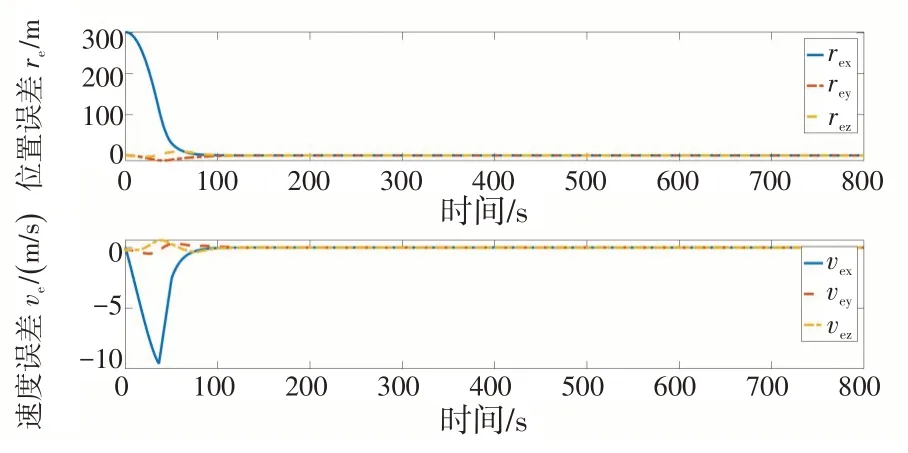
图1 相对位置和速度变化Fig.1 Relative position and velocity variation

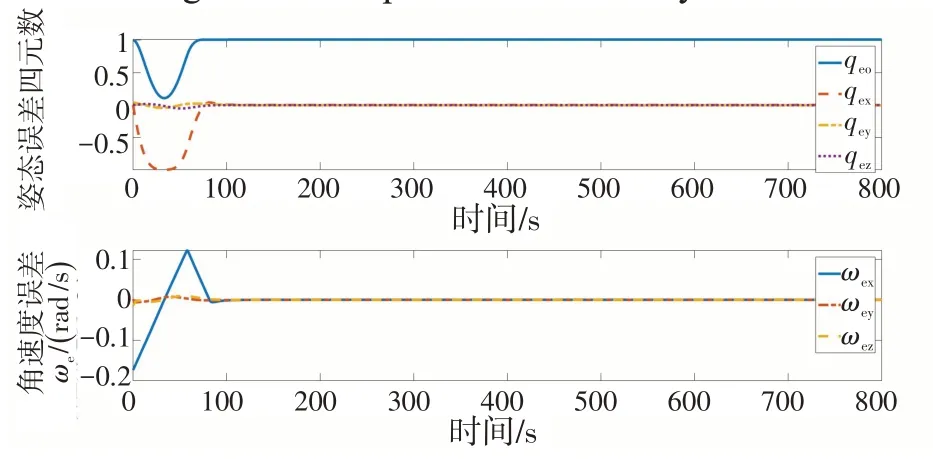
图2 姿态误差四元数和相对角速度变化Fig.2 Attitude error quaternion and relative angular velocity variation

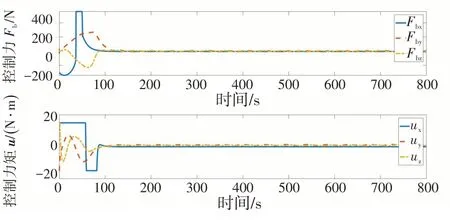
图3 控制力和控制力矩变化Fig.3 Variation of control force and torque

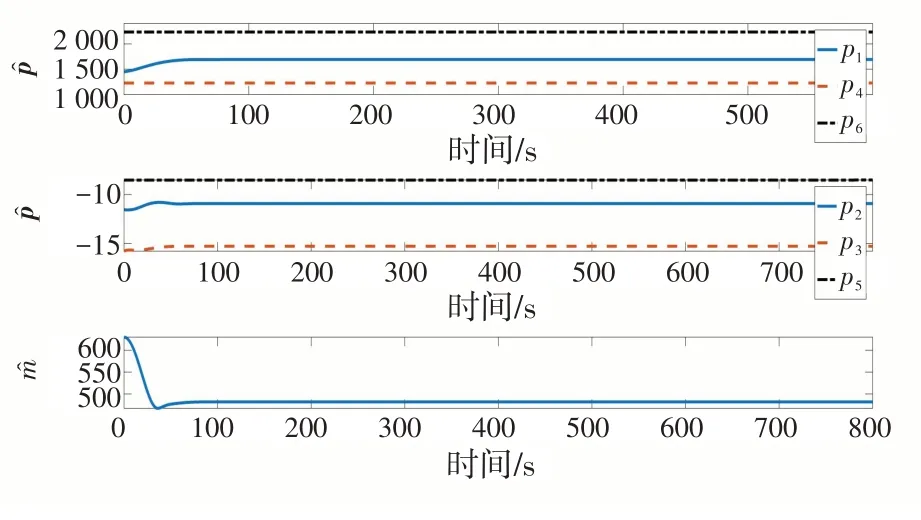
图4 和的变化Fig.4 Variation of estimates of inertia and mass parameters

情况2：目标器以ωd2的姿态角速度翻滚，仿真结果如图5～8所示。

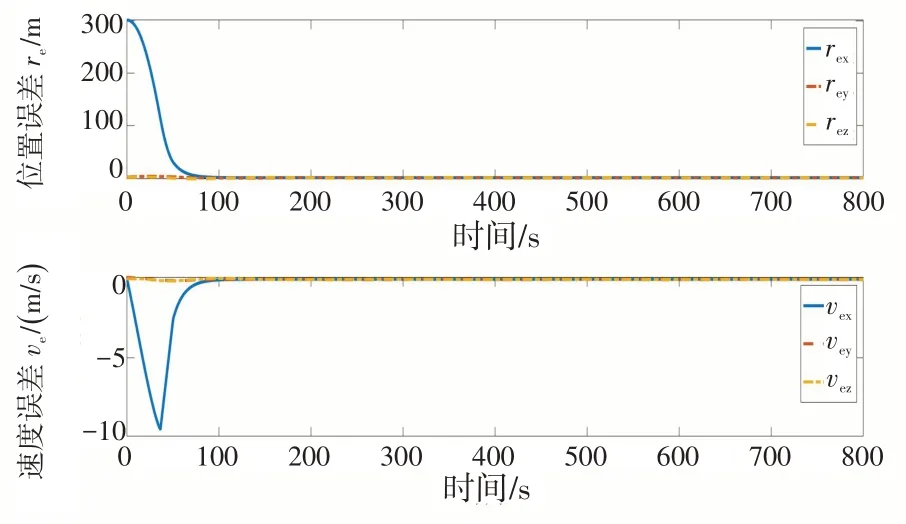
图5 相对位置和速度变化Fig.5 Relative position and velocity variation

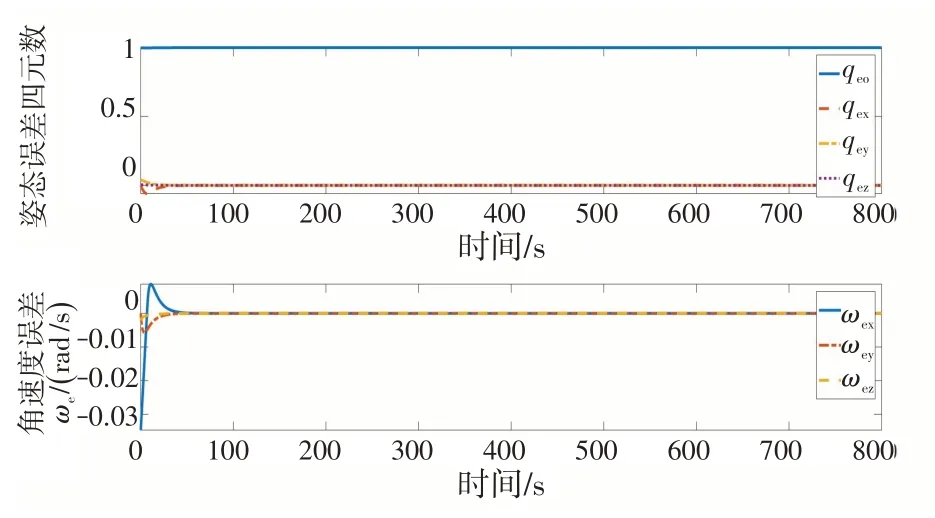
图6 姿态误差四元数和相对角速度变化Fig.6 Attitude error quaternion and relative angular velocity variation

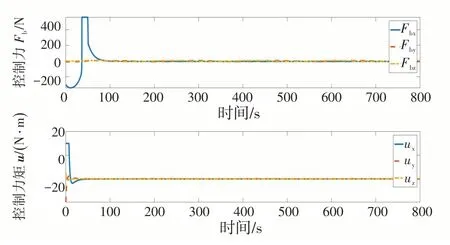
图7 控制力和控制力矩变化Fig.7 Variation of control force and torque

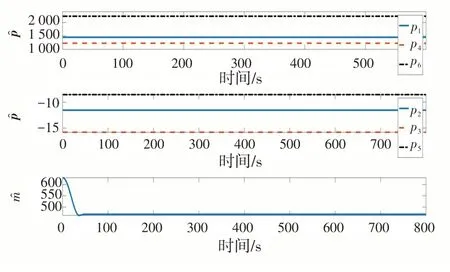
图8 和?的变化Fig.8 Variation of estimates of inertia and mass parameters

5 结论

本文针对翻滚非合作目标的近距离逼近与跟踪问题，建立了有限控制约束下的相对轨道和姿态动力学模型，在存在参数不确定性和外部扰动的情况下，设计了鲁棒自适应位置和姿态控制器，证明了系统是全局一致最终有界稳定的。仿真结果验证了该控制器的有效性，服务航天器在控制器作用下能够有效跟踪姿态变化较快的高速翻滚非合作目标，完成与目标的位置和姿态同步，并且该控制器不需要获得系统质量、惯量参数以及扰动上界的准确值，比较符合工程实际要求。