多孔石墨烯增强复合材料截锥壳的动力稳定性

黄小林,李粮杰,张燕宁,马 彬

(桂林电子科技大学 建筑与交通工程学院,广西 桂林 541004)

0 引 言

石墨烯增强功能梯度复合材料(Functionally Graded Graphene Platelets Reinforced Composites,FG-GPLs)是由石墨烯纳米片作为增强相沿一个或多个方向梯度分布于基体材料而制成的复合材料[1-3].相比于传统材料,FG-GPLs结构具有更加优异的物理机械性能,重量更轻,承载能力更高,可用于航天航空飞行器、潜艇、高速列车等工程结构.

目前关于FG-GPLs壳体稳定性的研究有有限元、Galerkin法等解析法和数值法.由于弹性模量等材料的物性参数在厚度等某一个/多各方向连续变化,用有限元分析往往需采用三维有限元,节点很多,计算量较大,故对于形状规则的FG-GPLs壳体结构,在建立其静/动力稳定的控制方程后用Garleikin法等解析法更简便.例如,Ansari等[4]用解析法研究了FG-GPLs圆筒壳的后屈曲问题,讨论了长径比和石墨烯分布模式对临界屈曲荷载的影响.Sun等[5]用辛分析法研究了多层FG-GPLs圆筒壳的扭转屈曲,发现壳体长度对临界屈曲荷载的影响较大,而壳体厚度的影响较小.此外,Chen等[6]分析过弹性介质中FG-GPLs夹心圆筒壳的屈曲特性,发现弹性介质对壳体屈曲行为有显著影响.由于制备技术的不足,FG-GPLs材料中常存在孔隙,且孔隙会影响结构的稳定性[7].因此,孔隙对壳体结构稳定性的影响是研究者们关注的焦点.基于Garleikin法,Shahgholian等[8]通过研究轴向荷载激励下含孔隙的FG-GPLs圆筒壳的屈曲特性,发现壳体边界条件和石墨烯纳米片的几何尺寸对临界屈曲荷载有较大影响.Zhou等[9]通过数值法和实验分析含孔隙的FG-GPLs圆筒壳的非线性屈曲,发现壳体的边界条件和面内约束对屈曲行为有显著影响.基于最小势能原理,Li等[10]研究了均匀径向荷载下含孔隙的FG-GPLs圆筒壳屈曲失效机理,得出孔隙会降低圆筒壳的临界屈曲压力.文献[11-12]采用一阶剪切变形理论研究了多孔FG-GPLs圆筒壳的屈曲行为,结果发现侧向压力和孔隙分布模式对圆筒壳临界屈曲荷载有较大影响.

综上所述,目前关于FG-GPLs壳体稳定性的研究大都集中于圆筒壳的屈曲,对圆锥壳特别是多孔截锥壳动力稳定性的研究很少,而且对多孔FG-GPLs材料的物性参数均直接假定了物性参数的分布.因此,本文根据孔隙的分布假定孔隙的体积组分,基于Halpin-Tsai微观力学模型计算物性参数,并通过Boltin法分析轴向激励和弹性介质作用下FG-GPLs截锥壳的动力稳定性,为该类壳体结构的设计提供理论基础.

1 截锥壳模型

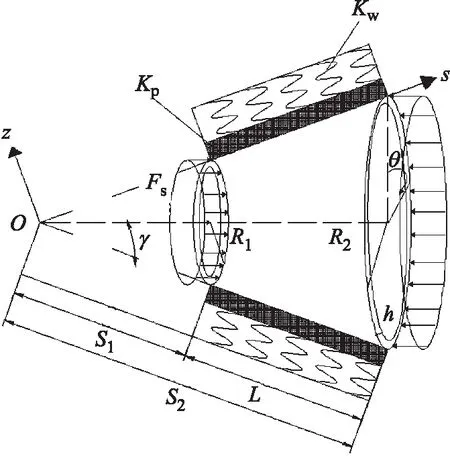
图1 弹性介质中FG-GPLs截锥壳 Fig.1 FG-GPLs truncated conical shell in elastic medium

如图1所示,采用正交曲线坐标系(s,θ,z),弹性介质中的石墨烯增强复合材料截锥壳受沿s轴方向均匀分布的周期荷载Fs(t)作用:

Fs(t)=FS+FDcos(ξt)

(1)

式中,FS为静载荷部分,FD为动载荷部分,ξ为激励频率.

设截锥壳临界屈曲荷载为Fcr,引入静载系数α=FS/Fcr和动载系数β=FD/Fcr,则有:

Fs(t)=[α+βcos(ξt)]Fcr

(2)

设壳体的半锥角、锥段长度和厚度分别为γ、L和h,小头半径和大头半径分别为R1和R2,挠度为w,弹性介质的压缩刚度和剪切刚度分别为Kw和Kp.忽略介质中阻尼和惯性力的影响,弹性介质对截锥壳的反作用力表示为:

式中,w为壳体中面的挠度。

由于金属等基体材料自身的原因或现有材料合成技术不足,FG-GPLs往往会产生孔隙,孔隙的分布类型也多种多样.为简化起见,本文只研究沿厚度方向的3种典型分布,如图2所示.图2(a)中P1为孔隙由中面向内外表面逐渐减少的类型;图2(b)中P2为孔隙由中面向内外表面逐渐增大的类型;图2(c)中P3为均匀分布类型.石墨烯纳米片沿厚度方向的分布有5种类型,如图3所示:从中面向内外表面逐渐非线性增多的G1型,从中部向内外表面非线性减小的G2型、均匀分布的G3型,从中面到内、外表面线性增多的G4类型和从中面向内外表面线性减少的G5型.图3中Si1、Si2、Si3、Si4和Si5分别为G1、G2、G3、G4和G5石墨烯分布下石墨烯体积含量的最大值.

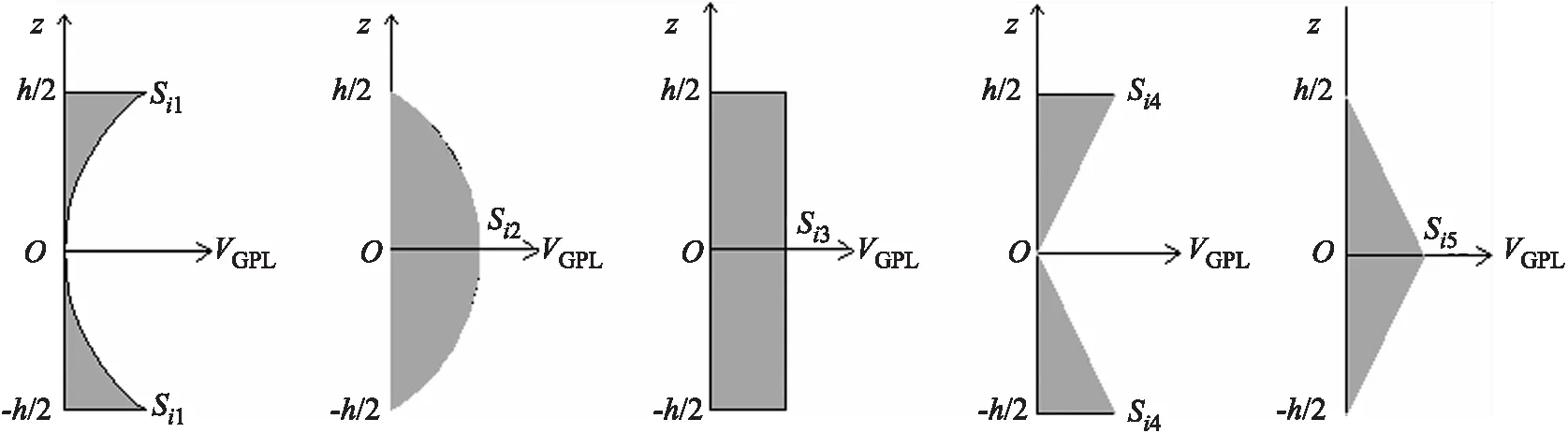
(a) G1分布 (b) G2分布 (c) G3分布 (d) G4分布 (e) G5分布

假设孔隙的体积组分:

(4)

截锥壳的密度:

式(4)和式(5)中:κ0、κ1和λ分别为P1、P2和P3分布的孔隙系数,ρ*为不含内部孔隙石墨烯增强截锥壳的密度,χ0,χ1和λ′分别为P1,P2和P3分布质量密度系数.

截锥壳的有效弹性模量、泊松比和剪切模量可表示为:

E(z)=E*(1-VP)

(6)

v(z)=v*(1-VP)

(7)

G(z)=G*(1-VP)

(8)

式中,E*、v*和G*分别为无孔隙截锥壳的杨氏弹性模量、泊松比和剪切模量.

由泡沫金属材料的弹性模量和密度之间的关系

由式(9)可得质量密度系数和孔隙系数的关系:

由(10)可看出,给定孔隙体积的分布系数κ0、κ1和λ可分别计算质量密度系数χ0、χ1和λ′.

假设不同孔隙分布壳的总质量相同,有:

根据式(11),给定孔隙系数(如κ0),其他孔隙系数可以确定.

无孔隙截锥壳的弹性模量、泊松比和密度分别用修正的Halpin-Tsai细观模型和混合律表示如下:

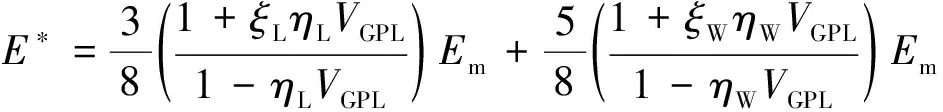
(12)

ν*=νGPLVGPL+νm(1-VGPL)

(13)

ρ*=ρGPLVGPL+ρm(1-VGPL)

(14)

式中:Em为基体材料的弹性模量,VGPL为石墨烯的体积组分,ρGPL和νGPL分别为石墨烯的质量密度和泊松比,而ρm和νm分别为基体材料所对应的值.ξL,ηL,ξW和ηW定义为:

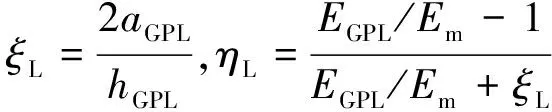
(15)

(16)

式中:aGPL、bGPL、hGPL分别为石墨烯纳米片的长、宽、高.

石墨烯的体积组分VGPL假设:

(17)

设5种GPL分布中石墨烯总含量相等,则有:

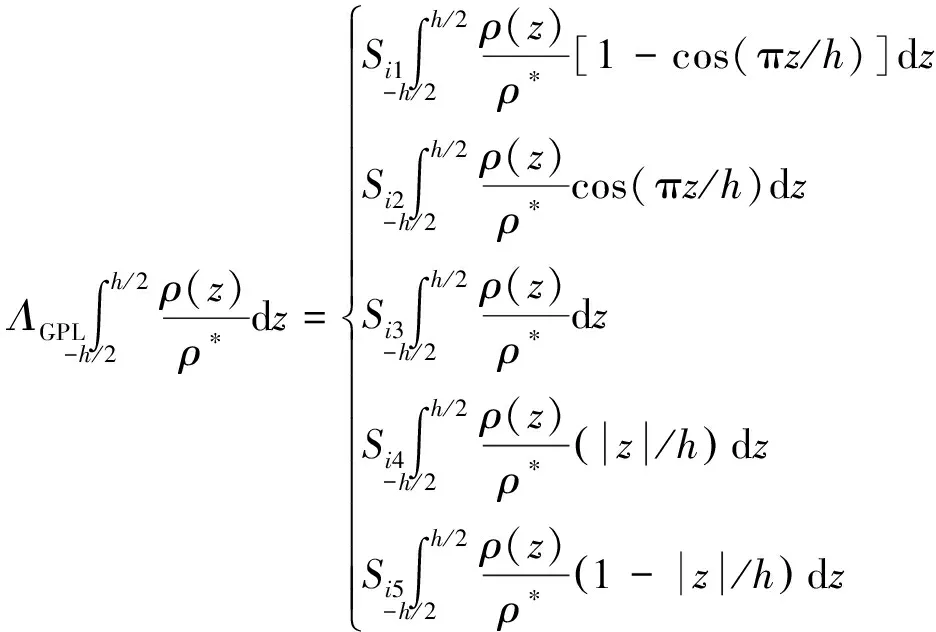
(18)

式中,ΛGPL为石墨烯的体积组分,可由质量组分WGPL计算:

2 控制方程及求解

引入变量φ=θsin(γ)和应力函数Φ.应力函数与面内力的关系为:

令s=S1ex,Φ=Φ1e2x,根据Donnell经典薄壳理论和Hamilton原理,可推导截锥壳振动的控制方程:

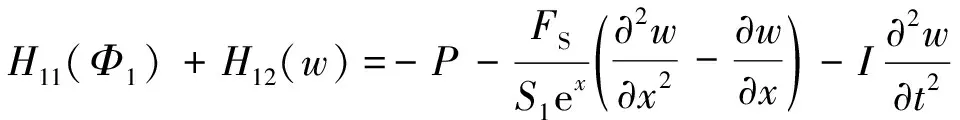
(21)

H21(Φ1)+H22(w)=0

(22)

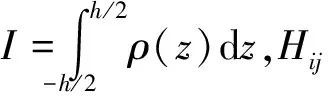
设截锥壳的边界条件为两端简支,则当x=0和x=x0时,w=Mx=0,其动挠度的形式解设为:

将式(23)代入式(22),由谐波平衡法可得应力函数的形式解:

(24)

式中,系数K1～K4见文献[13].将式(23)和(24)代入式(21),两边同乘以exsin(m1x)sin(n1φ),并进行Galerkin积分可得二阶线性微分方程组:

式中:M、Km和Kg分别为质量矩阵、刚度矩阵和几何矩阵,δ为位移系数向量即为[w11(t),w12(t),…,wm1n1(t),…].

式(25)为经典的Mathieu-Hill方程,描述了截锥壳在周期动荷载作用下的动力稳定行为.用Bolotin方法分析FG-GPLs壳体的动力不稳定区域.为求某一模态(m,n)下截锥壳的动力非稳定区域,将此模态下的δm1n1展开为奇数阶傅里叶级数,有:

式中:δ周期为2Tθ,Tθ=2π/ξ.

若将δ展开为偶数阶傅里叶级数,则有:

式(26)和(27)中,ak和bk均为待定系数.

对中面对称的混合板壳,根据非稳定区域的计算方法,周期为2Tθ的非稳定区域比周期为Tθ的更大[14],故本文只考虑周期为2Tθ的解.由于:

(28)

将式(28)～(29)代入式(26),由待定系数ak的正弦和余弦系数分别相等可得以下方程组:

将式(28)～(29)代入式(27),由系数bk的正弦和余弦系数分别相等可得以下方程组:

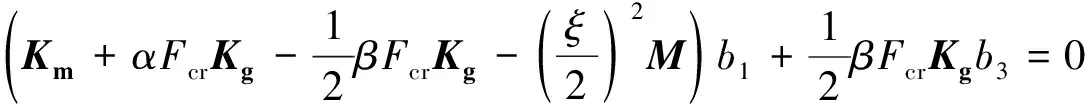
(32)

上述方程组如果有非平凡解,其系数矩阵对应的行列式应为零.若取一阶项k=1能满足精度要求,有:

其非平凡解应满足:

给定静荷载系数α,由公式(35)可计算动荷载参数β下截锥壳的临界激励频率,并得到非稳定区域的边界曲线β-ξ,β=0时的激励频率为临界激励频率.

3 算例比较和参数分析

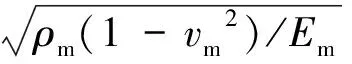
表1 各向同性截锥壳频率参数Ω的比较

图4显示了石墨烯增强圆筒壳固有频率随全波数n的变化曲线,并与文献[16]的结果进行了对比.当γ→0,S1→∞,S1sinγ=R,S2=S1+L,x0=L/S1时,截锥壳近似简化为圆筒壳.其中,石墨烯的弹性模量EGPL= 1 020 GPa,泊松比vGPL=0.3,密度ρGPL= 2 300 kg/m3.基体材料弹性模量Em=3 GPa,泊松比vm=0.34,密度ρm= 1 200 kg/m3.圆筒壳厚度h=2 mm,R/h=80,L/R=5,半波数m=1,石墨烯质量含量WGPL=1%,孔隙系数e0=0.2.图5计算了无空隙的石墨烯增强圆筒壳在轴向动荷载作用下的非动力稳定区域,并与文献[17]的结果进行了对比.圆筒壳的物性参数同图4,圆筒壳尺寸h=15×10-4m,R/h=20,L/h=10,取模态(m,n)=(1,1).

从前面的3个对比算例可看出,本文计算结果与相关文献的结果是比较接近的,说明本文的计算方法比较可靠,下面讨论石墨烯、孔隙等各种参数对石墨烯增强圆锥壳动力稳定的影响.

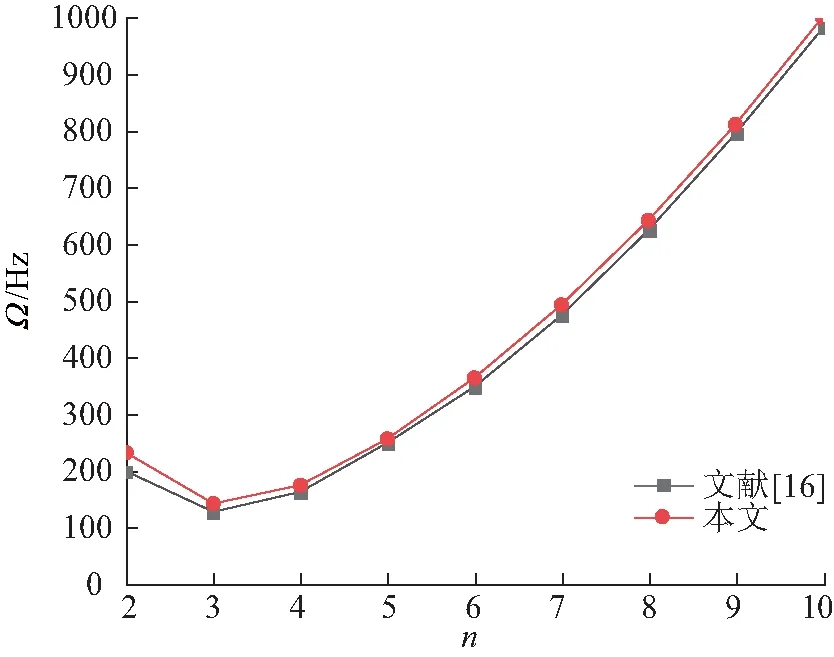
图4 多孔石墨烯增强圆筒壳的固有频率

3.2 参数分析

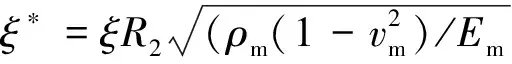
图6显示了半波数m和全波数n对临界激励频率ξ*的影响.由图可看出,临界激励频率ξ*随着半波数m的增大而增大.当全波数n从1变化到6时,临界激励频率ξ*也随之增大,而当n大于6时,临界激励频率随n的增大而减小,可见在模态(m,n)=(1,6)时,临界激励频率取得最小值.因此,后面的参数分析中取(m,n)=(1,6).

图6 半波数m和全波数n对临界激励频率的影响Fig. 6 Effects of half-wave number and full-wave number on critical excitation frequency

图7反应了石墨烯和孔隙分布模式对非稳定区域的影响.P1分布下5种石墨烯分布的临界激励频率分别为1.028、0.952、0.981、1.012和0.970,P2分布为1.009、 0.942、 0.966、 0.995和0.957,P3分别为1.021、0.948、0.976、1.006和0.965.可见,在5种石墨烯分布中,G1分布的临界激励频率最大,G2分布的最小.而在3种孔隙分布模式中,P1分布的临界激励频率最大,P2分布的最小.从图还可以得到,石墨烯和孔隙的分布模式对截锥壳的动力不稳定区域也有影响.在5种石墨烯分布中,G2的稳定区域最大,G1的最小.可见,G2的动力稳定性最好.

半锥角对非稳定区域的影响如图8所示.半锥角为10°、30°、50° 和70°时,临界激励频率分别为0.929、1.028、1.021和0.946,Δl为0.635、0.703、0.698和0.647.可见,半锥角为30°时,临界激励频率和非稳定区域最大,稳定性最弱.

(a) P1 (b) P2 (c) P3

图9分别考虑了静载系数α=0,轴向压力α=0.3和α=0.5,轴向拉力α=-0.5和α=-0.3对非稳定区域的影响.在轴向压力作用下,临界激励频率随轴向压力的增大而变小,而非稳定区域随轴向压力的增大而增大.在轴向拉力作用下,临界激励频率和非稳定区域均随轴向拉力的增大而增大.

图8 不同半锥角的非稳定区域

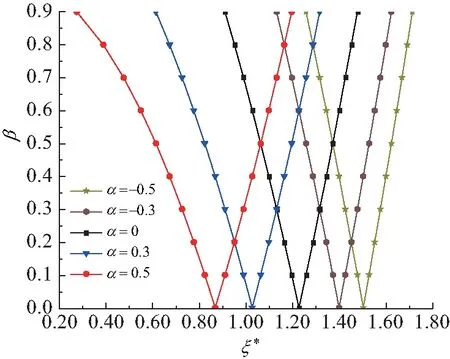
图9 不同静载系数的非稳定区域Fig. 9 Unstable regions under different static loads coefficients

图10显示了石墨烯含量对非稳定区域的影响.随着石墨烯质量含量的提高,临界激励频率和非稳定区域都增大,可见,石墨烯在提高截锥壳刚度的同时削弱了其稳定性.

如图11所示,当孔隙系数κ0从0.1变化到0.5时,临界激励频率和非稳定区域变化很小,对截锥壳的动力稳定性可以忽略.

弹性介质对非稳定区域的影响如图12所示.压缩和刚度参数(Kw,Kp)取(10,0)、(0,1)时,临界激励频率和非稳定区域比(0,0)大,且剪切参数Kp比压缩参数Kw对动力稳定的影响更大.

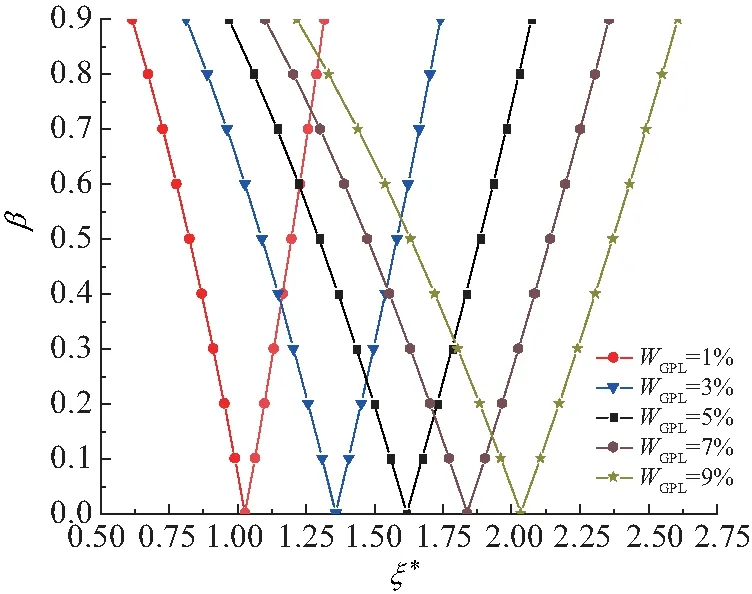
图10 不同石墨烯含量的非稳定区域

图11 不同孔隙系数的非稳定区域

图12 不同弹性介质的非稳定区域Fig.12 Unstable regions under different elastic medium

4 结 论

本文基于孔隙的体积组分,根据Halpin-Tsai微观力学模型计算了多孔FG-GPLs截锥壳的物性参数,用Boltin法计算了动力稳定区域的解析解,并讨论了石墨烯、孔隙等因素对截锥壳动力稳定的影响.主要结论如下:

1)3种孔隙分布中,P1类型孔隙分布的临界激励频率最大,在5种石墨烯分布中,G2分的临界激励频率和非稳定区域均最大;

2)轴向压力降低了截锥壳的临界激励频率,而轴向拉力增大了临界激励频率;

3)临界激励频率和非稳定区域随石墨烯质量含量的增大而增大;

4)在10°、30°、50°和70°半锥角中,30°的临界激励频率最大,但稳定性最差.

5)与压缩刚度相比,剪切刚度对截锥壳的动力稳定性影响更显著.