混合d-元树上的模式避免问题

杨胜良, 姜美杨

(兰州理工大学 理学院, 甘肃 兰州 730050)

树在组合数学中扮演着重要的角色.含有唯一的节点,使其成为有向树中其他所有后代的共同祖先,这样的树称作有根树.若对有根树每个分支点发出的边,按照从左到右(或从右到左)的方向进行标记,称这样的有根树为有序树.

在有序树中任意一个顶点到根点的距离叫做这个顶点的层,根点是0层上唯一的点.如果从顶点u到顶点v有一条边,则称顶点v为顶点u的孩子,顶点u被称作v的父顶点,顶点的度数是其孩子的总数.叶点是度为0的点,即没有孩子的顶点,出度至少为1的顶点称作内点.当树中只包含叶点时,这样的树称作平凡树.

d-元树是有序树的一种,其中每个顶点的度数为0或d, 特别地,当d=2时,这样的树称作2-元树.在d-元树中对每个内点用黑色或白色着色,所得的标号树叫做混合d-元树.为了与黑色的内点进行区分,用ε标记叶点.在一个混合d-元树中,称为边的一种模式,如果一个内点和其最左端的儿子都着黑色.若混合d-元树中没有出现该模式的边,称为避免模式混合d-元树.

例1图1给出有7个内点,避免模式的2-元树.

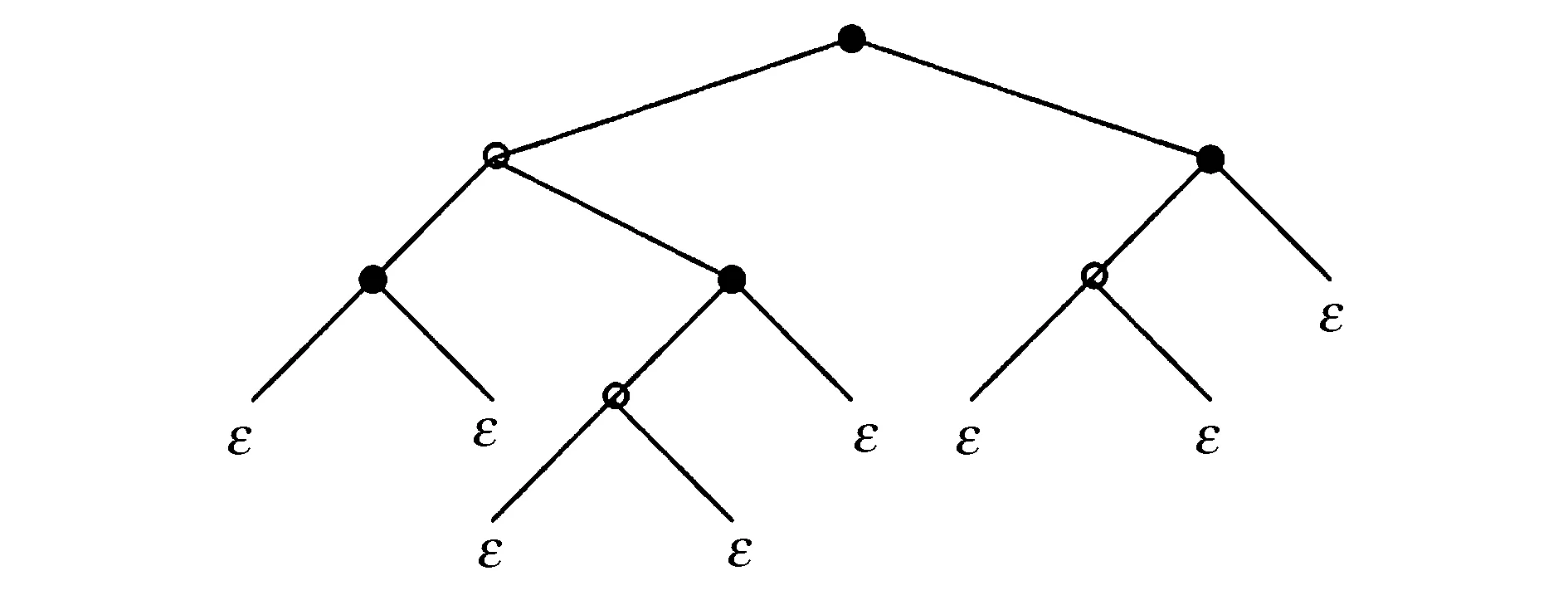
图1 避免模式混合2元树

Gu等[1]提出避免模式的2-元树是混合2-元树,并考虑了几类避免其他模式的2-元树.Panholzer等[2]研究了避免模式的d-元树,Hong等[3]对混合2-元树进行了推广,提出避免模式混合d-元树,更多相关研究见文献[4-6].

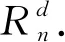
引理1[8](拉格朗日反演公式) 设f=f(t)是一个由f=tφ(f)定义的形式幂级数,其中φ(t)是一个φ(0)≠0的形式幂级数.对于任何形式的幂级数F(t)有

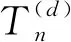
图2 标记内点时避免模式混合d-元树的分解

设B(t)为根点是黑色树的发生函数,W(t)为根点是白色树的发生函数,由图2可得

所以发生函数T(t)为

两边同时乘以d-1次方可得

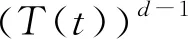
由拉格朗日反演公式得

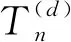
表的前部分值

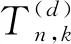
证明用t标记内点,x标记黑色的内点,由符号化方法可以得到图3的分解.

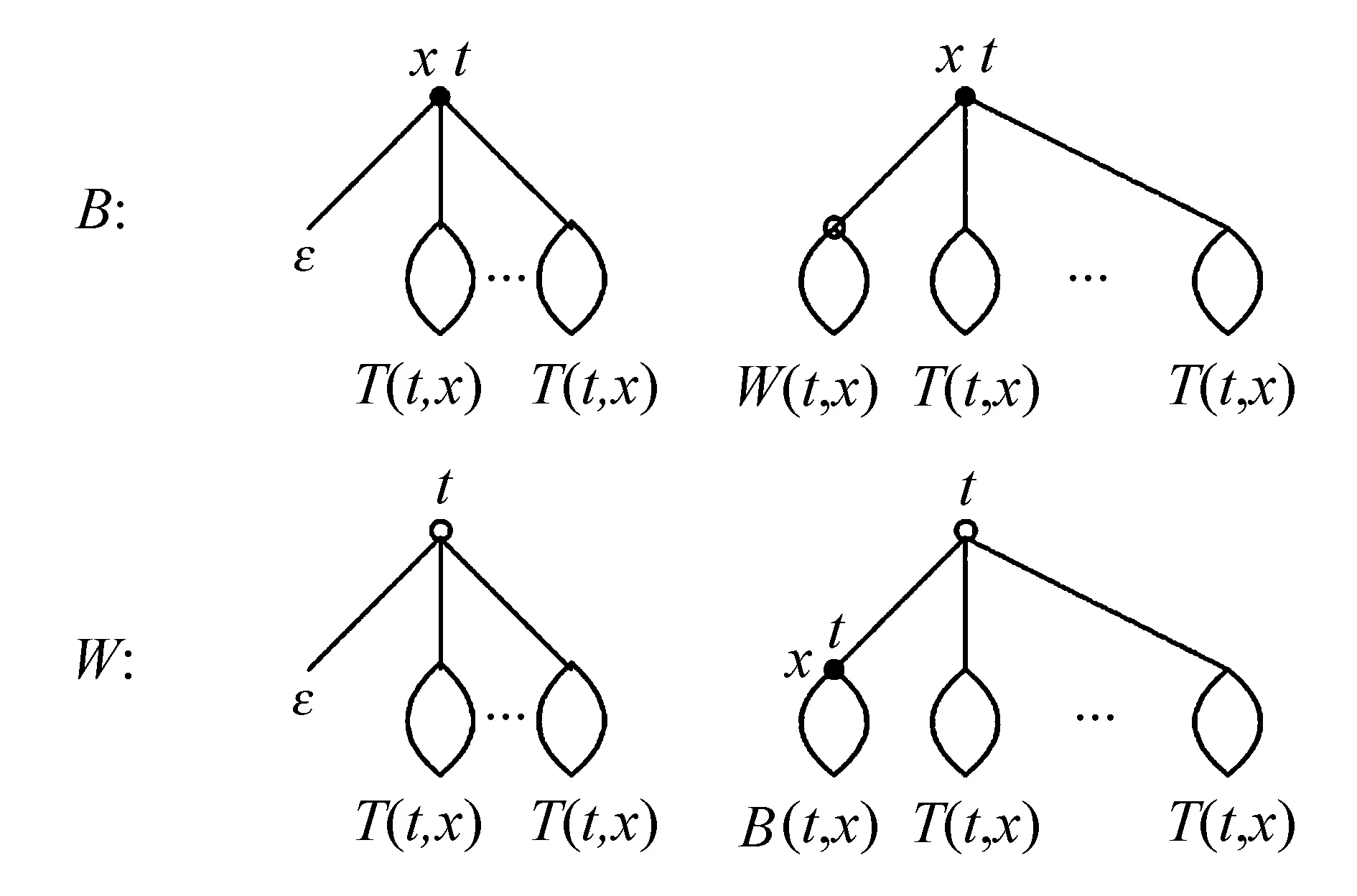
图3 标记黑色内点时避免模式混合d-元树的分解

设B(t,x)为根点是黑色树的发生函数,W(t,x)为根点是白色树的发生函数,由图3得

B(t,x)=xtT(t,x)d-1+xtT(t,x)d-1W(t,x)

W(t,x)=tT(t,x)d-1+tB(t,x)T(t,x)d-1

B(t,x)=xtT(t,x)d-1+x(1+

B(t,x)(tT(t,x)d-1)2)

W(t,x)=tT(t,x)d-1+x(1+

W(t,x)(tT(t,x)d-1)2)

(1)

(2)

由式(1,2)可得

两边同时乘以d-1次方得

设f(t)=t(T(t,x))d-1, 则

由拉格朗日反演公式得

下面给出双射的证明.

由图2易知,W中的任何一个白色根点都有一个最左边的子树B和d-1个子树T1,T2…Td-1.同样B中的任何一个黑色根点都有一个最左边的子树W和d-1个子树T1,T2,…,Td-1.通过前序遍历构造长度为dn的d-Schröder路:

1) 访问一个黑色内点时:

(1) 当最左边的子树为平凡树时,对应于UUT′1UT′2…D(d)T′d-1.

(2) 当最左边的子树不为平凡树时, 对应于UW′UT′1UT′2…D(d)T′d-1.

2) 访问一个白色内点时:

(1) 当最左边的子树为平凡树时,对应于UT′1UT′2…H(d)T′d-1;

(2) 当最左边的子树不为平凡树时,对应于UB′UT′1UT′2…D(d)T′d-1.

3) 对子树W,B,T1,T2…Td-1继续重复1),2)过程,直到子树为平凡树为止.

其中U表示上步(1,1),D(d)表示下步(1,1-d),H(d)表示水平下步(2,2-d)W′,B′,T′1,T′2…T′d-1是W,B,T1,T2…Td-1相对应的d-Schröder路的子集, 该过程也在图4中给出.

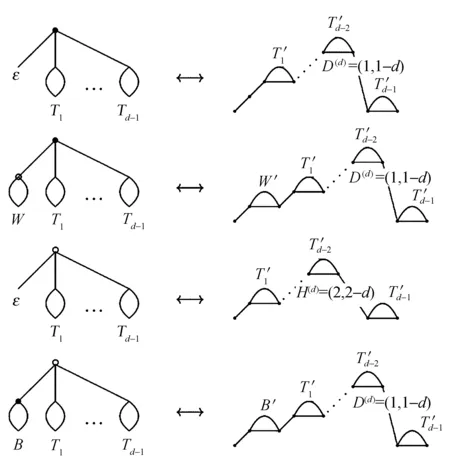
图4 避免模式混合d-元树与d-Schröder路的双射

由于每个d-元树经过上述分解后所得到的子树都不相同,故对应所得的d-Schröder路也不同,满足单射.

图5 避免模式混合3-元树与3-Schröder路的双射

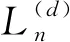
定理4有n个内点避免模式混合d-元树的个数为

证明用t标记内点,x标记黑色的内点, 由符号化方法可以得到图6的分解.

图6 标记内点时避免模式混合d-元树的分解

由图5得到发生函数为

L(t)=1+tL(t)d-1+t2L(t)2d-1+tL(t)d

化简可得

两边同时乘以d-1次方得

设f(t)=t(L(t))d-1,

由拉格朗日反演公式得

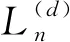
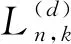
定理5有n个内点k个黑色内点的避免模式混合d-元树的个数为

证明用t标记内点,x标记黑色的内点,由符号化方法可以得到发生函数为

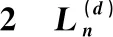
表的前部分值

化简可得

两边同时乘以d-1次方得

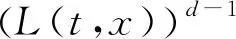
由拉格朗日反演公式得

从而得到

例5避免模式混合3-元树的发生函数为L(t,x)=1+xtL(t,x)2+xt2L(t,x)5+tL(t,x)3,具有n个内点k个黑色内点避免模式混合3-元树的个数为

证明用t标记内点,由符号化方法可以得到图7的分解.

图7 标记黑色内点时避免模式混合d-元树的分解

设B(t)为根点是黑色树的发生函数,W(t)为根点是白色树的发生函数,由图7可以得到

两边同时乘以d-1次方得

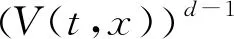
由拉格朗日反演公式得

表的前部分值

证明用t标记内点,x标记黑色的内点,由符号化方法可以得到

可得

两边同时乘以d-1次方得

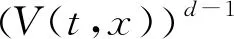
由拉格朗日反演公式得

从而得到