半间歇式沸腾床反应器中液相循环速度的测定

王伟伟，张建鹏，岳 志，黄子宾，程振民

（华东理工大学化学工程联合国家重点实验室,上海 200237）

随着人类开采的原油量的不断增加，优质油田储量不断下降，原油中重质组分不断增多。由于重质油相比优质原油含有更多的硫、氮、重金属等物质，在加氢反应过程中极易造成催化剂积碳、中毒、失活[1]，因而人们对重质原油加氢技术的要求不断提高。重质油加氢反应器主要有固定床、悬浮床和沸腾床3 种类型。现阶段，沸腾床渣油加氢技术在国外工业化应用中发展较好，主要有H-Oil 和LC-Fining两种工艺技术路线[2]。沸腾床是一种气-液-固三相催化反应器，具有结构和操作相对简单、无机械传动装置以及总体温度均匀等特点，可用于渣油加氢、费托合成、甲醇合成等化工过程[3]。

多相流反应器内部物料的流体力学行为与其自身物系以及反应器结构密切相关，且存在显著的放大效应。沸腾床虽然在多数情况下相比其他反应器类型有良好的性能，但是作为多相流反应器，目前还没有足够的理论指导，反应器结构设计、放大和操作过程仍需建立经验模型并进行大量实验，或使用计算流体力学软件进行模拟研究[4]。对气-液-固三相体系来说，其流体力学行为在宏观上的区分有操作类型、相对流动方向、气液相连续性，表征参数有气含率、固含率、气液速、气泡上升速度、气泡直径大小、颗粒形状及大小等[5-9]。

与鼓泡塔一样，在气-液-固三相沸腾床中同样存在液体和固体的循环流动，这是由于气含率沿塔径向分布不均匀造成的，这种循环有利于流体的传质和传热。在沸腾床中，气泡带动固体和液体在塔中央向上流动，近壁处固体和液体向下流动[10]，形成整体的大循环，而在部分区域可能会因湍动的液相形成局部循环[11-12]。当体系固含率较低且固体颗粒的粒径较小时，固体的循环速度可以由液体的循环速度代替。这是因为较低固含率下固体之间的相互作用较小，固体受自身作用影响较小，其运动主要由液体带动[13-15]。这样，液体循环速度可近似为固体循环速度，固体循环速度越大，说明固体颗粒在反应器中的分布效果越好，混合越均匀。

本文旨在研究半间歇式沸腾床反应器中液体循环速度的影响因素。与直接测量液体速度的方法不同，本文所得到的是宏观液体循环速度，而非特定点处的液体速度。本文采用示踪剂法，通过求解轴向扩散模型得到液相轴向扩散系数，根据爱因斯坦扩散系数定义式求得液体循环速度，研究不同表观气速和固含率对液体循环速度的影响。

1 轴向扩散模型

轴向扩散模型是一种非理想流动模型，适用于返混程度不大的体系，常用于描述管式和塔式反应器内流体的流动模型。该模型在流动方向上添加了一个轴向扩散项，即由分子扩散、对流扩散、湍流和不均匀的速率分布而带来的轴向返混。使用示踪剂法测定沸腾床的轴向扩散模型系数，示踪剂的轴向扩散可使用一维扩散模型进行描述[16]：

Levenspiel[17]指出在轴向扩散较小的情况下，无论是闭式系统还是开放系统，示踪剂浓度曲线的形状对施加的边界条件都不敏感。文献[18-23]表明，不管示踪剂注入的是理想脉冲还是其他浓度曲线，都只会改变模型的边界条件而不会改变模型参数。因此，可以在装置入口处注入一定量示踪剂，在装置某处对其浓度进行精准测量，将这条浓度曲线假设为这一点处示踪剂的输入边界条件，并在其下游某处测量另一条浓度曲线作为出口响应，通过处理两条浓度曲线即可求解出轴向扩散系数。

本研究为半间歇式操作，实验过程中没有主体流动，u=0 ，则可将式(1)简化为

初始条件为

边界条件为

其中，C0(t) 为示踪剂输入浓度曲线函数。

通过爱因斯坦扩散系数定义式计算液体循环速度，关系式如下[24]：

式中：De为扩散系数，l为扩散长度，θD为扩散时间。

假定l等于床层高度h，则液体循环速度可表示为ul=h/θD，那么式(6)可表示为

这样就可以通过液体轴向扩散系数求得宏观上的液体循环速度。

2 实验部分

2.1 试剂与仪器

氯化钾（w=99.5%），上海泰坦科技股份有限公司；氮气，福联科技气体(昆山)有限公司；电子天平，YP-3002，精度0.01 g，上海越平科学仪器有限公司；气体涡轮流量计，LWGQ-60AT，上海虹益仪表设备有限公司；液体涡轮流量计，LWGY-50BT，上海虹益仪表设备有限公司；螺杆空压机，R901U-AT，上海英格索兰压缩机有限公司。

2.2 实验装置

沸腾床中试实验装置如图1 所示。结构采用中国石化抚顺石油化工研究院研发的STRONG 技术[25]，塔身由有机玻璃制成，整塔尺寸为Φ300 mm×7200 mm，壁厚7 mm。

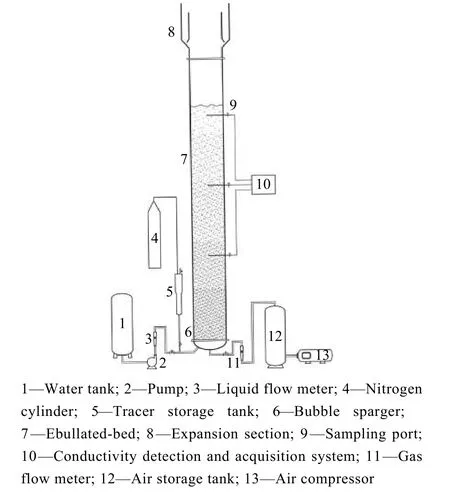
图1 沸腾床实验装置Fig.1 Ebullated bed experimental device

采用水、空气、Al2O3颗粒作为三相体系，颗粒为球形，平均粒径0.4 mm。Al2O3颗粒由塔顶加入，水经由泵从塔底打入，气体由压缩机加压从塔底封头进入，经由泡罩式分布器进行分布再进入塔段，最后从塔顶逸出。整个实验过程中液体和固体均不进料和出料。

2.3 实验流程

注入一定量的水和催化剂颗粒，使得通气后床层高度大约为5 m，固体颗粒添加量分别按照固含率（体积分数）12%、15%、20%、30%进行添加。气体由一台空压机提供，流量由气体涡轮流量计进行控制和测量，表观气速范围0.086 ～ 0.216 m/s。采用示踪剂法对塔内液相的轴向扩散系数进行测定，注入方法为脉冲注入法。

水和催化剂颗粒加入塔内后，首先将气体从塔底通入，稳定20 min，使沸腾床内流动状态趋于稳定，并记录床层高度。将2000 mL 质量浓度为25 g/L的氯化钾溶液倒入示踪剂罐，打开氮气钢瓶，氮气充入示踪剂罐，使罐内压力达到0.4 MPa 左右。沸腾床稳定后，分别在沸腾床的1.8、3.2、4.8 m 高度处通过取样管取出塔中心处液体进行电导率测定。打开塔底部示踪剂注入阀1～2 s，氯化钾溶液被氮气压入塔内，开始计时，直到电导率曲线趋于平缓后停止计时。由于塔内氯化钾质量浓度非常低，其电导率与浓度的变化符合线性关系，则根据式(8)将电导率转换为质量浓度，得到示踪剂浓度曲线。

其中A为浓度转换系数，本实验中所使用电导率仪的浓度转换系数为0.5。

本文采用的轴向扩散模型（式（2））为一维动态二阶偏微分方程，通常使用数值法求得其数值解。在MATLAB 中可使用偏微分方程（PDE）工具箱，输入初始条件和边界条件进行求解。初始条件见式(3)。第1 个边界条件见式(4)，将1.8 m 处的示踪剂响应曲线作为浓度输入曲线函数C0(t) ，z1=1.8 m；第2 个边界条件为Neumann 边界条件，见式(5)，z2=4.8m。由于轴向扩散系数未知，因此需要使用非线性回归法进行参数估计。本文采用非线性最小二乘法，将3.2m 和4.8m 处的示踪剂浓度曲线数据代入进行参数估计，即可求得液相轴向扩散系数。将液相轴向扩散系数代入式(7)可得到宏观液体循环速度。

3 结果与讨论

3.1 示踪剂响应曲线

不同固含率和表观气速下沸腾床1.8 m 和4.8 m处的示踪剂响应曲线如图2 所示。从图2 可以看出，示踪剂注入后10 s 或15 s，1.8 m 处才测得到示踪剂。再经过20～25 s，塔顶4.8 m 处才测得到示踪剂。说明示踪剂从塔底注入后是按轴向进行运动，到达塔顶后沿壁面再向下流动。图2 中示踪剂质量浓度曲线随时间增加趋于平缓，这是由于实验过程中没有液体和固体的进出，在经过一定时间混合后塔内各处示踪剂浓度为一个定值。同时由图2 可以看出，表观气速越大，示踪剂质量浓度增加越快，浓度曲线越快接近最大值，说明表观气速的增大能够增加示踪剂在轴向的运动速度，加强反应器的混合效果。

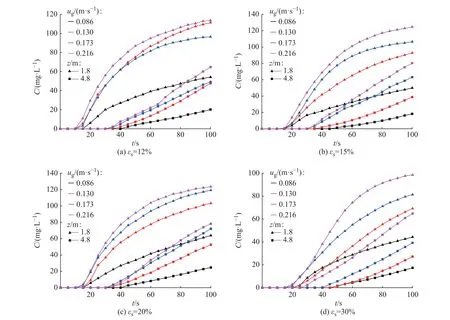
图2 不同固含率和表观气速下沸腾床1.8 m 和4.8 m 处示踪剂响应曲线图Fig.2 Response curves of tracer at 1.8 m and 4.8 m of the ebullated-bed under different solid holdups and different superfical gas velocities

3.2 液体循环速度

不同固含率下液体循环速度与表观气速的关系如图3 所示。在同一固含率下，随着表观气速的增加，液体的循环速度近似线性增加。由于本实验没有表观液速，则塔内液体的循环流动是由气泡的上升运动所带来的。当表观气速增加时，气泡逐渐由小气泡并聚成为大气泡，气泡的上升速度和动能增加带动液体使液体循环速度增加，这与前人研究结果相吻合[26-31]。

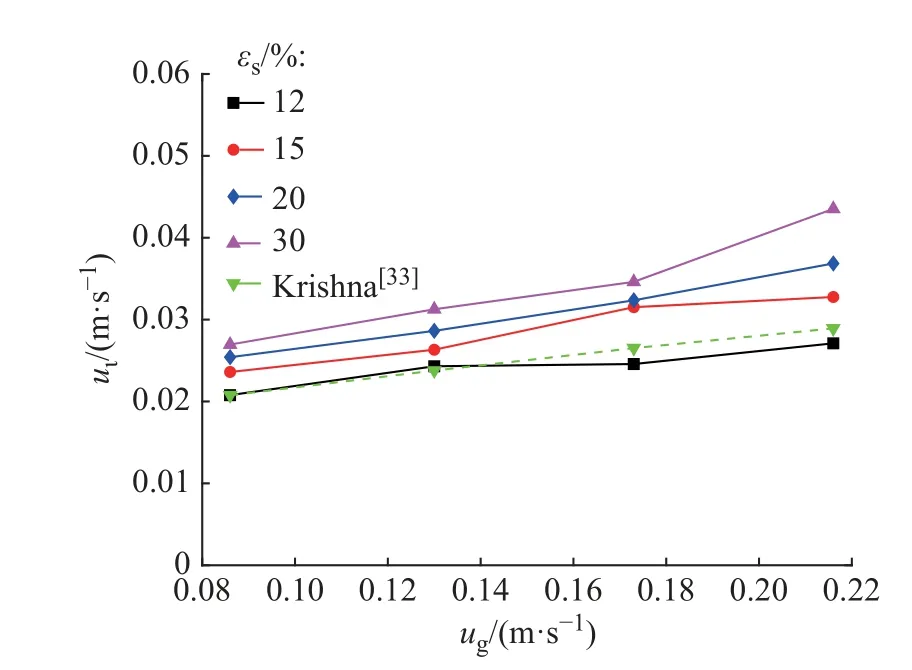
图3 不同固含率下液体循环速度与表观气速的关系Fig.3 Relationship between the liquid circulation velocity and superfical gas velocity under different solid holdups

程振民等[32]在一套直径3.0 m、高36.86 m 的中试装置中测定了液相轴向扩散系数。在表观气速0.086 m/s、固含率12%时得到的液相轴向扩散系数为1.7 m2/s，代入式(7)得到液体循环速度为0.092 m/s，与本实验同条件下的数值（0.021 m/s）差距较大，可能是由于装置的放大效应导致明显的数据差异。Krishna 等[33]在直径0.38 m、固含率18%的鼓泡桨态床中给出了液相轴向扩散系数与中心液速和塔直径的关系式：

中心液速的关联式由Riquarts 等[34]提出：

其中，vl为液相运动黏度，本文取水的运动黏度vl=10−6m2/s。通过此关系式计算得到液相轴向扩散系数并代入式(7)中，所得液体循环速度如图3 中虚线所示，可以看出本实验结果与Krishna 等[33]的研究成果相符。

不同表观气速下液体循环速度与固含率的关系如图4 所示。可以看出，随着沸腾床固含率的增加，塔内液体循环速度也随之增加。在固含率较低时，增加固含率可以明显加快液体的循环速度。朱闯杰等[35]指出当固含率低于29.3%时，大气泡上升速度和大气泡摩尔分数随着固含率的增加而增大，塔内小气泡摩尔分数随之减小。由于液体主要随着大气泡向上流动，因而大气泡上升速度的增大增加了液体循环速度。在固含率较大时，液体循环速度的增加变得缓慢，这可能是由于固含率增大时，体系的黏度随之增大，阻碍了液体的循环流动。Smith 等[36]将液体黏度和固含率两个影响因素进行关联，定义了浆态流体的黏度，其值与液体黏度和固含率相关。固含率越高，浆态流体黏度越大。气泡的上升速度会受流体黏度的影响，流体黏度越大，气泡上升速度越小，最终导致液体循环受阻，这与Li 等[37]的研究结论相似。

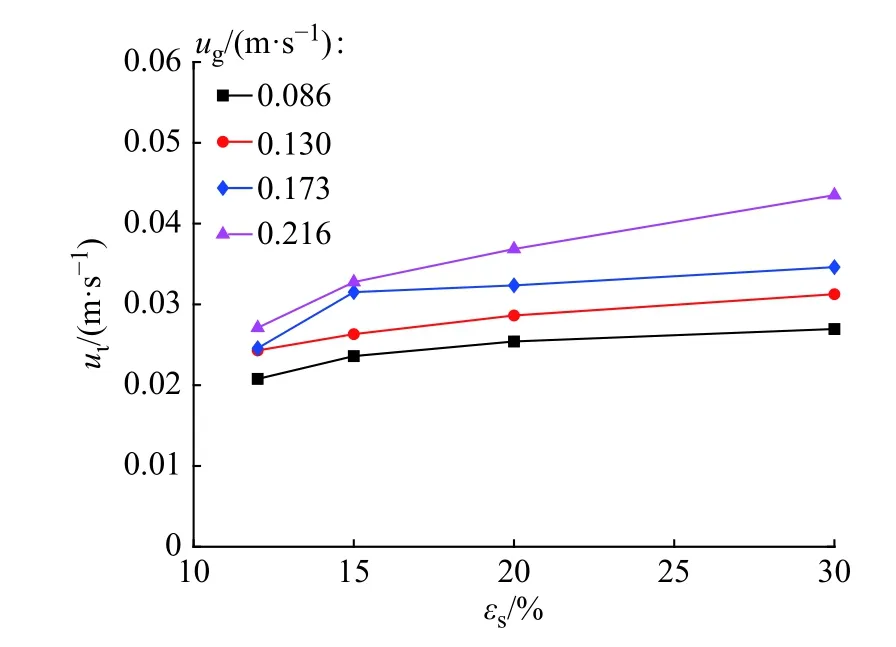
图4 不同表观气速下液体循环速度与固含率的关系Fig.4 Relationship between liquid circulation velocity and solid holdup under different superficial gas velocities

3.3 模型求解曲线的拟合效果

为验证轴向扩散模型是否适用于本研究体系，将塔顶4.8 m 处的实验测定点与轴向扩散模型求解曲线进行相关性分析（图5），得到的相关系数均大于0.98，相对误差小于10%。从图5 中可以明显看出模型求解曲线与实验点相吻合，说明模型求解结果很好地反映了示踪剂浓度的实际变化情况。

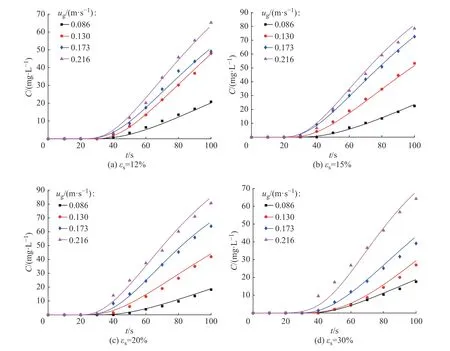
图5 塔顶示踪剂质量浓度求解曲线与实验点曲线图Fig.5 Mass concentration curve of tracer and experimental point curve at the top of tower

4 结 论

在气-液-固三相沸腾床冷模反应器中研究了固含率（12%～30%）和表观气速（0.086～0.216 m/s）对塔内液体循环速度的影响，结论如下：

（1）采用示踪剂法通过轴向扩散方程和爱因斯坦扩散系数定义式可求得液体循环速度，从而提供了一个测量宏观液体循环速度的方法。

（2）在固含率一定的条件下，随着表观气速增加，小气泡逐渐聚集成大气泡，气泡上升速度不断增大，液体循环速度也不断增大，说明增大表观气速可以明显提高液体循环速度。

（3）当表观气速一定时，随着固含率的增加，大气泡增多，气泡上升速度也增加，液体循环速度也随之增大。由于固含率的增大会在一定程度上阻碍液体的循环流动，因此随着固含率的增加，液体循环速度的增量不断减小，说明固含率可能存在一个最优值。

符号说明：