基于镜像空间的平移嵌入模型

葛学伟，范贵生,2，虞慧群,2

（1.华东理工大学计算机科学与工程系, 上海 200237；2.上海市计算机软件测评重点实验室, 上海 201112）

知识图(Knowledge Graphs, KGs)作为描述现实世界的方法之一，是许多语义应用程序的核心技术，其广泛应用于问题回答[1]、搜索和自然语言处理。知识图不仅有表达知识结构的能力，还能够帮助关系推理。近年来，知识图领域发生了许多理论创新，使得许多下游应用也得到了蓬勃发展。

然而，现实世界的知识图通常是不完整的，有必要进行知识图补全或链接预测。学习知识图中实体和关系的低维表示已经被证明是完成这一任务的一个很好的方法[2]。

在知识图中，数据可以表示为三元组（Triplets）的集合，将每个三元组 (h,r,t) 表示为一个首实体h和尾实体t之间的关系r。所有首实体h和尾实体t构成了实体集ε，所有关系的集合为关系集 R。知名的现有数据集有Freebase[3]，Yago[4]，WordNet[5]等。到目前为止，根据知识图中已有的信息来预测缺失关系已有相关模型，比如TransE、ComplEx，但许多基于TransE 的模型会将对称关系学习为 0 向量，因此，无法做到有效区分[6]，而以ComplEx 为代表的模型则大大增加了复杂度。

本文提出基于镜像空间的平移嵌入模型MTransE，它不仅学习了对称和反对称关系的表示，对模型内的对称关系进行了有效区分，而且该方法适用于所有基于平移的嵌入模型；同时它与复数表示相比，减少了参数的规模。实验表明，该方法在4 个完备的知识补全数据集上都具有良好的性能。

1 相关工作

知识图的向量嵌入（Embedding）工作在近年来受到普遍关注。嵌入方法主要分为基于三元组的嵌入模型和基于路径的语义模型。

基于三元组的嵌入模型TransE[2]被广泛应用于知识图的嵌入，它将关系解释为向量空间内的平移，即h+r≈t，后续提出的许多模型都在此模型上进行了改进和完善。为了改善TransE 模型在一对多、多对一、多对多模型上的局限性，TransH 模型将首尾节点根据不同关系进行拆分，利用节点在关系向量方向的投影，使得同一个实体在不同的关系下有了不同的表示[7]。TransR 模型认为对于不同关系，实体应该具有不同的语义空间，应将首节点和尾节点投影到关系对应的空间内进行运算[8]。TransD 模型则认为，虽然TransR 对首尾节点进行了空间变换，但由于首尾节点本身所处的空间属性并不完全相同，因此该模型使用两个矩阵对首尾节点分别进行了空间变换[9]。

基于路径的语义模型包括双线性模型如DistMult[10]、HolE[11]、ComplEx[12]和其他基于神经网络的模型。这些方法通过匹配实体和关系的潜在语义对知识图建模。RESCAL 模型用方阵表示关系[13]，而DistMult 用对角阵降低复杂性。SimplE 模型也是一种简单而有效的知识图嵌入双线性方法[14]。HolE模型研究全息的简化表示，并利用循环相关性来捕捉实体之间复杂的相互作用。在ComplEx 模型中，将实体和关系嵌入到复空间中，并用厄米积对反对称模式进行建模，在学习KGs 表示方面取得了很好的效果。许多基于神经网络的方法也被应用到实验中，例如ER-MLP和神经张量网络[15]。一些其他类型的神经网络，如卷积神经网络、图卷积网络和深度记忆网络[16]在此任务中也表现出了良好的性能。

本文提出的MTransE 模型通过将镜像空间的概念运用于平移的嵌入模型中，补充了对知识图中广泛存在的3 种关系模式进行模拟的能力。该概念亦可应用于其他基于平移的嵌入模型。

2 基于镜像空间的平移嵌入模型

本文MTransE 模型介绍了知识图中链接预测的3 种重要的关系模式，并提出了模型在镜像空间中的距离计算方法；同时说明MTransE 简单有效，能够推断3 种关系模式，并且该方法也可用于其他基于平移的模型。

MTransE 采用经典的嵌入模型结构作为基本框架：首先，数据集提供成批的三元组作为原始输入，通过不同的嵌入度量，得到不同的嵌入向量，这里首实体和尾实体的嵌入矩阵相同，皆为实体嵌入矩阵，而关系嵌入单独设置嵌入矩阵；其次，将嵌入后的向量输入评分计算层，其内部的评分函数是嵌入模型的核心，它决定了嵌入向量在向量空间中的分布。表1 所示为各个嵌入算法的打分函数和复杂度，其中，k为嵌入空间的维度，Rk为k维的实数空间，Ck为k维的复数空间，b为镜像空间的大小，Re(·)为实部运算，mod 为联模运算，Otime为时间复杂度。得到评分后通过自适应负采样计算得到平衡后的损失，最后按照学习率进行损失的反向传播。

表1 算法打分函数及其复杂度Table 1 Scoring functions of algorithms and their complexities

2.1 关系模式

如文献[6]中所指出，知识图中链接预测的关键是推断出链接模式，具有模式建模能力的模型效果更好。在知识图中广泛存在3 种重要的关系模式：对称和反对称、相反以及组合。通常，它们的定义如下：

若一个关系r是对称（反对称），则 ∀x,y∈ε ：

若一个关系r1和关系r2相反，则 ∀x,y∈ε ：

若关系r3是关系r1和关系r2的组合，则 ∀x,y,z∈ε ：

2.2 原始空间

基于计算机表达的有限性，如64 位浮点数的表示范围为 −21024∼21024，实际应用的模型并不能真正地将数据嵌入到无限的向量空间中，实际的向量嵌入总是在有限的向量空间内。因此，可以指定变量表达范围内的某一子空间为原始空间，定义原始空间为：

其中B=[0,b),b∈R ，n为空间维度。

2.3 镜像空间

在本文模型中，实体和关系被映射为镜像空间中的向量，这个镜像空间是原始空间和自身的镜像的组合。定义原始空间的镜像为其本身进行尺寸整数倍平移所形成的空间，即：

镜像中的点yi=(y1,y2,···,yn) 与原始空间中的点xi=(x1,x2,···,xn)满足：

其中，ki∈Z ，Z 为整数集；b为原始空间的尺寸。

此外，定义所有由同一个原始空间中的点经过上述平移得到的点互为镜像点。如果点v和点v′互为镜像点，则：

其中，| ∗| 为按元素取绝对值。

2.4 基于镜像空间的嵌入

给定一个三元组 (h,r,t) 的集合S，其中h,t∈ε（实体集），r∈R （关系集），本文模型将同时学习实体和关系的嵌入向量。与TransE 类似，本文将实体表示为空间内的一点，将关系表示为空间中的一个平移向量。与此同时，当 (h,r,t) 为真时，h+r与t的最近镜像点尽可能近；当 (h,r,t) 为假时，h+r与t的最近镜像点尽可能远。因此，距离函数定义为：

其中，t∗为最近的镜像点。作为TransE 的变种，MTransE 不仅可以模拟和推测知识图中的相反和组合关系，而且通过镜像空间，MTransE 也获得了推测对称关系的能力。

负采样在学习知识图嵌入和单词嵌入中被证明非常有效。负样本由破坏数据集的首节点或尾节点而来，其不存在于原有数据集中。利用自对抗性负抽样技术和计算的分值，对每个三元组进行权重分配，分数越高，权重越大。对负样本三元组的权重分布安排如下：

其中，上标“'”表示不在原数据集。下标i，j分别为所有负样本和某一个负样本。fr(·,·) 是打分函数，{(hi,ri,ti)}是所有三元组的集合，α是训练温度（给定值）。因此得到了如下形式的负采样损失：

其中，γ 是一个固定边距，α(·) 为函数。

2.5 MTransE 模型

基于镜像空间的嵌入模型MTransE 算法如下：

本算法通过破坏对象的主体来生成测试集的负样本，并且确保这些负样本没有出现在数据集的混合集。

对称关系在二维平面上的嵌入示意图见图1。从图1 可以看到，实体h通过对称关系r的2 次转换，被投射到了它的镜像点h′；而在TransE 模型中，由于不存在镜像点，为了保证两次对称变换可以回到等效原点，关系r将被建模为0。因此MTransE 解决了TransE 中无法区分对称关系的问题。

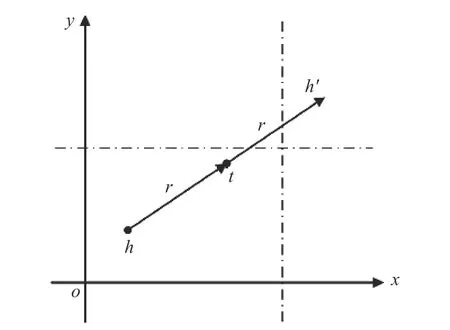
图1 对称关系在二维平面上的嵌入示意图Fig.1 Embedding diagram of symmetric relations in a twodimensional space

3 实验结果与分析

3.1 数据集

FB15K、WN18、WN18RR、FB15K-237 等是被广泛使用的数据集，本文采用这几个知识图进行实验，表2 示出了数据集的规模和划分情况。其中WN18是从WordNet3（WordNet3 是一个英语词汇数据库，单词通过概念语义和词汇关系相互连接）中提取的数据集；WN18RR 是从WN18 中去掉了逆关系的子集；FB15K 是从Freebase（一个大型元组数据库，具有结构化的一般人类知识）中抽取的关系三元组数据集；FB15K-237[17]则是在FB15K 上去除了相反关系的数据子集。

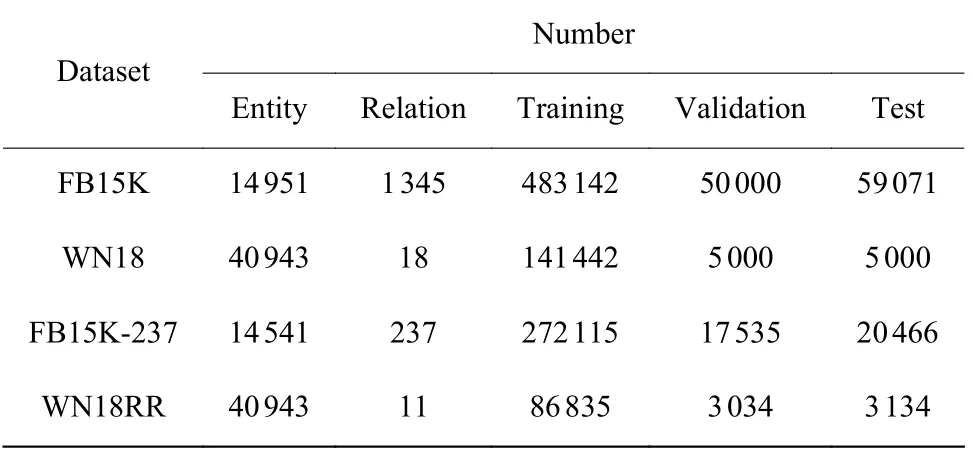
表2 实验数据集Table 2 Experiment datasets

3.2 实验设置

本文评估了TransE、Ho1E、DistMult 和MTransE这4 个数据集，并对其平均排序 (MR)、平均倒数（MRR）、第N次命中率 (Hit@N)等性能进行测试。

由于MTransE 是TransE 的直接变种，本文使用TransE 作为比较基线，而RotatE 模型[6]是将关系建模作为复数空间中的旋转使其具有学习对称与反对称模式的能力，因此本文也与RotatE 模型进行了比较。在语义匹配方面，采用了DistMult 和HolE 作为比较模型。

本文在文献[6]的源代码的基础上进行修正，并在单个GPU (Nvidia GeForce RTX 2080)进行测试，同时使用Adam 作为优化器，在验证数据集中尝试了多个超参数配置，进行网格搜索的超参数的选择范围为：嵌入维数k∈{500, 800,1 000} ，批次大小b′∈{256,512}，自对抗性采α样 ∈{温0.5,1度.0}，固定边界γ ∈{18,24,30}。实体嵌入向量归一初始化于整个向量空间，而关系的嵌入向量归一初始化于原始空间，采用早停止的策略来防止过拟合。

3.3 结果与讨论

本文得到了MTransE 的实验数据，其他的报告数据则来自文献[6，18]。

表3 和表4 分别示出了各个模型在数据集FB15K 和WN18 上的实验结果。由表可得，MTransE获得了优于其他基线模型的实验性能，主要原因是FB15K 和WN18 中的主要关系模式是对称和反对称以及相反，相比于TransE 将对称关系嵌入为 0 ，MTransE能有效地分辨这些关系。

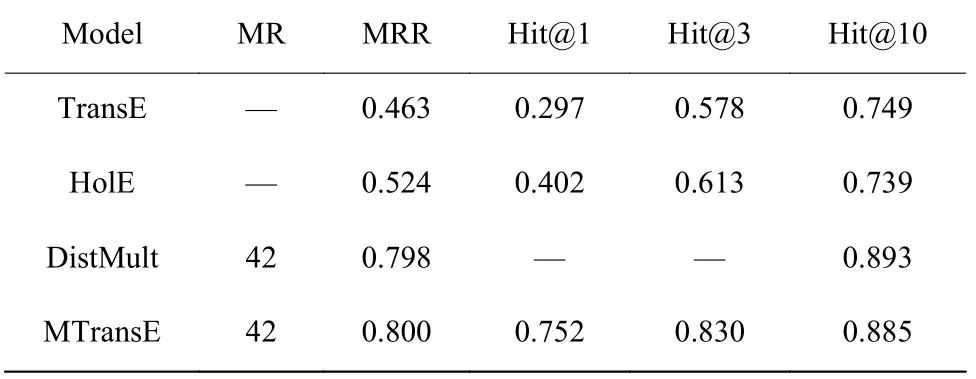
表3 数据集FB15K 上的实验结果Table 3 Results on dataset FB15K

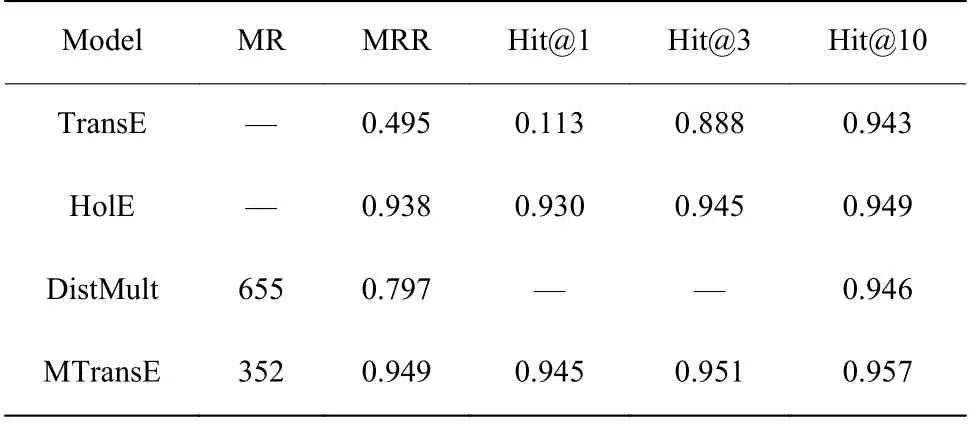
表4 数据集WN18 上的实验结果Table 4 Results on dataset WN18

表5 和表6 分别示出了各个模型在FB15K-237和WN18RR 上的表现。由表可知，MTransE 的表现依然优于大多数基线模型，但优势不明显。原因是这两个数据集主要包含组合关系和其他未知关系，这些未知的关系在本文模型中没有得到目的性的解决。然而，与本文模型的基础模型TransE 相比，MTransE在这些数据集上的表现仍然更好。这是因为像同义词这样的对称关系通过组合等其他关系依然隐藏在于数据集中，这使得MTransE 获得了更好的预测性能。

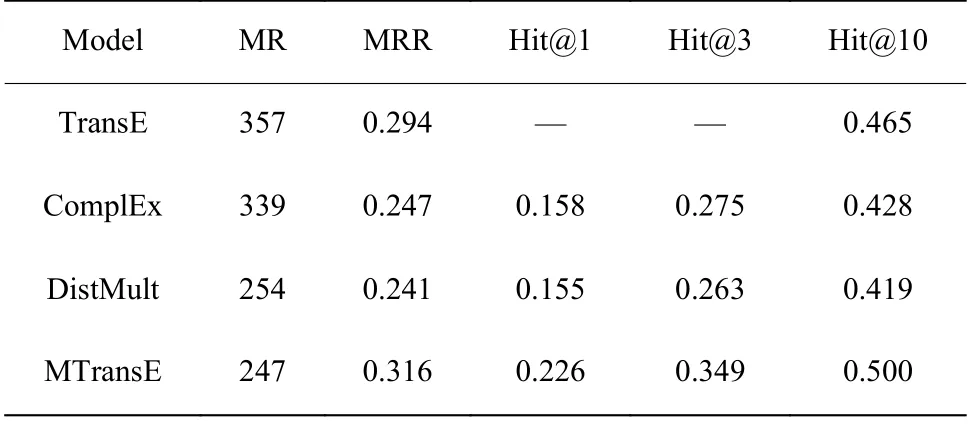
表5 数据集FB15K-237 上的实验结果Table 5 Results on dataset FB15K-237

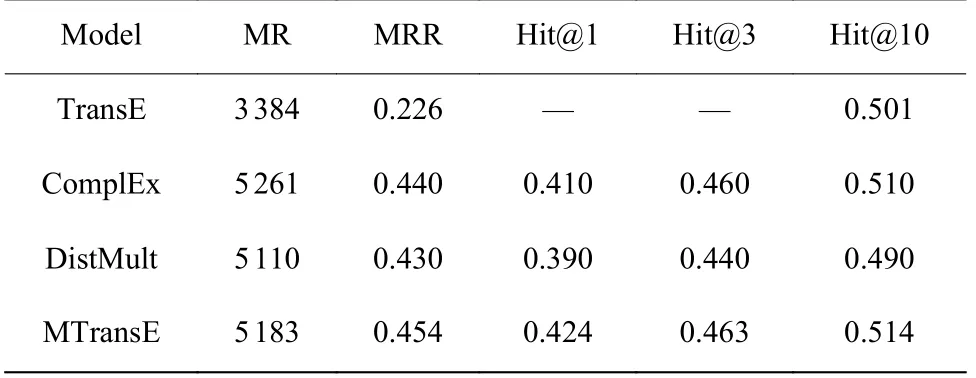
表6 数据集WN18RR 上的实验结果Table 6 Results on dataset WN18 RR

3.4 模型分析

MTransE 源自于TransE，并加强了它推断对称关系的能力，且与RotatE 非常相似，并且在实验上达到了相同的性能水平。相比于RotatE，MTransE 镜像空间的概念可用于所有基于TransE 的嵌入模型。

相比于TransE，MTransE 可以模拟和推断对称关系，而TransE 不能。如果TransE 中的关系r是对称关系，则有:

即所有对称关系的嵌入为向量 0。而在本文的模型中，如果一个关系r是对称关系，则有：

式中，r可以为 (k1b,k2b,···,knb) ,ki∈Z ，任何满足于该条件但不线性相关的向量都代表了不同的对称关系。

3.4.1 MTransE 和RotatE 的相似性 RotatE 模型中的关系被模拟为复数空间中的旋转，并且在RotatE的源代码中，关系向量实际上表示为相位（其模长固定为1），而实体向量由实部和虚部两部分表示。模型一旦优化完成，h◦r≈t（◦ 为复数乘法）的关系几乎在所有地方都成立，又由于r的模长固定为1，因此 |h| 和 |t| 几乎相等。也就是说，如果一个知识图是完全连接的，模型得到的所有嵌入向量模长相同。这也是文献[6]中RotatE 的变体（若将实体模量限制为常数的pRotatE 模型）能达到几乎与原模型相同效果的原因。

不考虑所有常数，则pRotatE 的距离函数可表示为：

式中，θh为首实体的相位，θr为关系的相位，θt为尾实体的相位。

设 ∆θ=θh+θr−θt，则有

本文MTransE 模型将关系建模为镜像空间中的平移，其距离函数为:

其中t∗为t最近的镜像点，即t∗=kb+t,k∈Z。

设 ∆x=h+r−t，则有

可以看到，dr(h,t) 是一个周期函数，其中一个周期 ∆x∈[0,b) 有如下情形：

即dr(h,t)=min(b−∆x,∆x) ，其中，∆x∈[0,b)。

令 ∆z=|h+r−t|modb，则

图2 所示为RotatE 和 MTransE 距离函数的对比图像，其中RotatE 的距离函数为MTransE 的距离函数为dr(h,t)=π−|π−(|∆x|mod 2π)|。从图2 可以看出，当恰当设置参数时，MTransE 和RotatE 的距离函数表现出一致的周期性和单调性。表7 和表8 也分别示出了这两个模型具有相似的性能表现。本文比较了这两个模型的一维距离函数（打分函数），同时可以推测其他具有相同周期性和单调性的距离函数具有相似的性能。

图2 [−8π，8π]中的距离函数图像Fig.2 Distance functions in [−8π，8π]

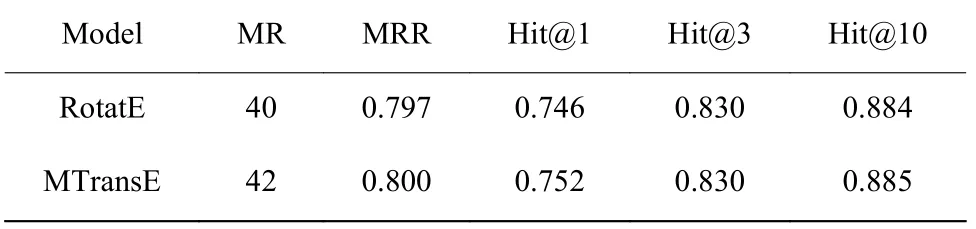
表7 RotatE 和MTransE 在FB15K 上的实验结果Table 7 Results of RotatE and MTransE on FB15K

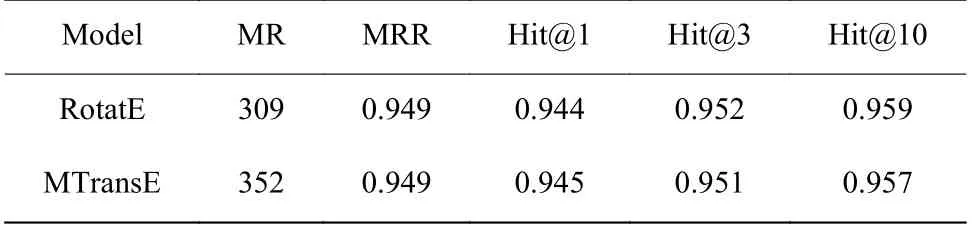
表8 RotatE 和MTransE 在WN18 上的实验结果Table 8 Results of RotatE and MTransE on WN18

3.4.2MTransE 的优势 与TransE 相比，本文模型克服了TransE 不能对对称关系进行建模的不足，而对称关系在许多知识图中是非常重要的。与RotatE 相比，本文模型使用线性函数来建模距离，这意味着可以在所有基于平移的嵌入模型中使用镜像空间的核心概念，如TransD、TransH 等模型。而在模型大小方面，MTransE 只采用了RotatE 一半的参数就可以达到类似性能。

4 结 论

本文设计了一种新的知识图嵌入模型，该模型将关系模拟为镜像空间中的平移操作，直观且易于可视化。对比于TransE，本文模型具有对对称关系模式建模的能力。在4 个广泛使用的数据集上的实验结果表明，MTransE 具有良好的性能，在参数设置较少的情况下，依然优于多个近期有较强性能的比较基线。本文提出的核心概念−镜像空间，也可用于许多其他基于TransE 的模型。