高超声速火箭橇刨削效应仿真与验证研究
夏洪利,刘振,闫华东,赵项伟,孟鑫
(1. 西安交通大学航天航空学院,710049,西安; 2. 中国兵器工业试验测试研究院,714200,陕西华阴)
火箭橇试验能够为全尺寸、全质量状态被试载荷提供气动、振动、热环境等高超声速动态条件,是高超声速飞行器开展地面高动态试验的有效方法。火箭橇通过滑靴与钢轨约束配合,由于靴轨间存在一定的间隙,火箭橇沿滑轨高速滑行时,会附加产生俯仰、偏航、滚转3个自由度的运动,其中任一运动均会导致滑靴以极高速度冲击轨道。当火箭橇速度接近5Ma左右时,该冲击作用会引起靴轨接触表面温度急剧升高,致使靴轨材料软化,产生大变形和塑性流动[1-2]。塑性流动射流导致靴轨材料发生混合以及伴随着产生空穴,使得滑靴或滑轨表面产生“凹坑”,形成刨削现象[3]。刨削会造成靴轨配副环境劣化、稳定性降低,是制约火箭橇试验运行速度提升的重要因素之一[4]。
针对高超声速火箭橇试验中极易出现的刨削现象,国外相关机构如美国空军技术研究院、德克萨斯大学、桑迪亚国家实验室很早便开始关注并开展了大量的理论研究工作。20世纪60年代末和70年代初,Gerstle在桑迪亚国家实验室对高超声速单轨火箭橇试验中出现的刨削现象进行了研究[5-7],研究发现,非均匀变形的轨道不平顺度及凸起会形成冲击波,进而产生刨削。典型刨削现象如图1所示。

图1 典型火箭橇刨削现象[8]Fig.1 Typical gouging phenomenon of rocket sled
Gerstle进一步对轨道刨削坑处的金相组织进行了研究,发现轨道(1080钢)的表面生成了一层马氏体组织,马氏体组织上沉积了一层滑靴材料(304不锈钢),并且在刨削坑内发现了垂直和平行于火箭橇橇车运行方向的绝热剪切带。金相分析表明,刨削形成过程是一个热力学事件,伴随着材料的相变和急剧温度变化,靴轨接触产生了足够高的温度,使珠光体奥氏体化,然后迅速淬火生成马氏体层;剪切带的形成释放了内部产生的热量,并且在刨削形成的过程中发生了靴轨材料混合。Mixon[9]对低质量拦截弹(LMI)、中等质量拦截弹(MMI)和“爱国者”PAC3导弹火箭橇试验中的刨削的位置、刨削发生时的橇体速度、刨削的数量和大小等进行了归纳统计。根据统计结果推测,影响刨削发生的因素包括动态载荷引起的高应力、火箭橇运行速度、轨道表面粗糙度、摩擦热、滑靴材料劣化、滞留在靴轨间隙的碎片,以及气动热引起的火箭橇材料软化等。
国外关于刨削问题的数值计算主要应用美国Sandia国家实验室开发的CTH代码[10-13]。CTH程序采用欧拉-拉格朗日方法,求解过程分为两步:第一步是拉格朗日步,即网格随物质运动发生变形;第二步是欧拉步,变形的物质网格被映射回欧拉背景网格。结合由试验得到的滑靴材料和轨道材料的非线性本构关系,CTH程序可以模拟刨削过程,但其基本算法过程报道的较少。Sulsky等[14-15]修改了应用于流体力学中的物质网格粒子元胞法和隐式粒子流体法,并将其扩展运用到固体力学当中,将其命名为物质点法(MPM)。它采用拉格朗日质点和欧拉网格双重描述,将连续体离散成一系列连续质点。该方法可以避免欧拉法中因非线性对流项产生的数值困难并容易跟踪物质界面,同时能够避免拉格朗日法中因网格畸变而产生的数值困难。物质点法因其独特的特点,对分析刨削问题具有优势。
国内开展高超声速火箭橇刨削现象研究较晚,目前西安交通大学在该领域研究较为深入。张静静[16]以物质点算法为研究手段,从滑块运行过程中结构的等效应力及轨道表面粗糙度两方面出发,给出了刨削发生时的判断条件。汪振兴[17]、干聪等[18-19]基于物质点理论,建立了火箭橇系统二维模型和靴轨二维平面应变模型,分别开展了竖向临界速度的影响规律和滑靴温度变化对刨削临界条件的影响研究,但该研究仅停留在数值仿真层面,计算结果的准确性未经试验验证。
鉴于国外对我国的技术封锁,国内刨削研究因缺少真实试验数据仅以理论仿真为主的现状,本文以高超声速火箭橇刨削效应在轨试验为基础,分析刨削试验现象,建立了靴轨材料的热黏塑性Johnson-Cook本构模型,基于物质点方法并结合火箭橇试验真实刨削数据,开展了刨削分析与验证的闭环研究,阐述了刨削效应形成的机理。
1 高超声速火箭橇刨削效应在轨试验
试验在国内某单位火箭橇滑轨上进行。试验采用单轨三橇结构,通过三级动力将载荷加速至高超声速。试验滑轨为U71Mn材质的起重机钢轨,第三级火箭橇通过4部滑靴与滑轨约束,滑靴材质为30CrMnSiNi2A,靴轨配合为干摩擦滑配合。刨削发生时,火箭橇系统质量约为600 kg,靴轨上下总间隙约为4.2 mm,左右总间隙约为5.5 mm。火箭橇系统示意如图2所示。

图2 国内某型火箭橇试验系统示意图Fig.2 Diagram of a domestic rocket sled test system

图3 国内某型火箭橇试验刨削现象Fig.3 Gouging phenomenon of a domestic rocket sled test
试验成功验证了刨削现象。试验后对滑轨进行细节观察,发现在火箭橇运行高速段,不同位置出现不同程度的刨削现象。典型刨削如图3所示,刨削坑位于轨道踏面上,长约220 mm,宽约18 mm,深度约1.8 mm,形貌呈纺锤形,两侧窄中部宽,分内外环,外环表面呈现金属干摩擦样貌,短时间内出现锈蚀;内环表面呈现熔融金属冷却样貌,外表形成黑色氧化层,与外环相比,不易锈蚀。
2 高超声速火箭橇刨削效应数值研究方法
2.1 靴轨材料热黏塑性Johnson-Cook本构模型
基于数值分析方法开展刨削问题研究时,首先需要获取滑轨材料在中高温、高应变率、大变形下准确的动态力学模型。基于U71Mn滑轨材料流动应力响应对温度和应变率表现出的较强敏感性,选用Johnson-Cook本构模型描述材料的热黏塑性力学行为[20-25]如下
(1)
本文基于静态拉伸试验(试验结果如图4所示)和高温双同步Hopkinson杆试验(试验装置如图5所示,试验结果如图6所示),开展Johnson-Cook本构模型研究。

图4 U71Mn静态拉伸试验真实应力-应变曲线Fig.4 True stress strain curve of static tensile test for U71Mn

图5 高温双同步Hopkinson杆试验装置Fig.5 A Hopkinson bar experimental device based on the principle of high temperature double synchronization
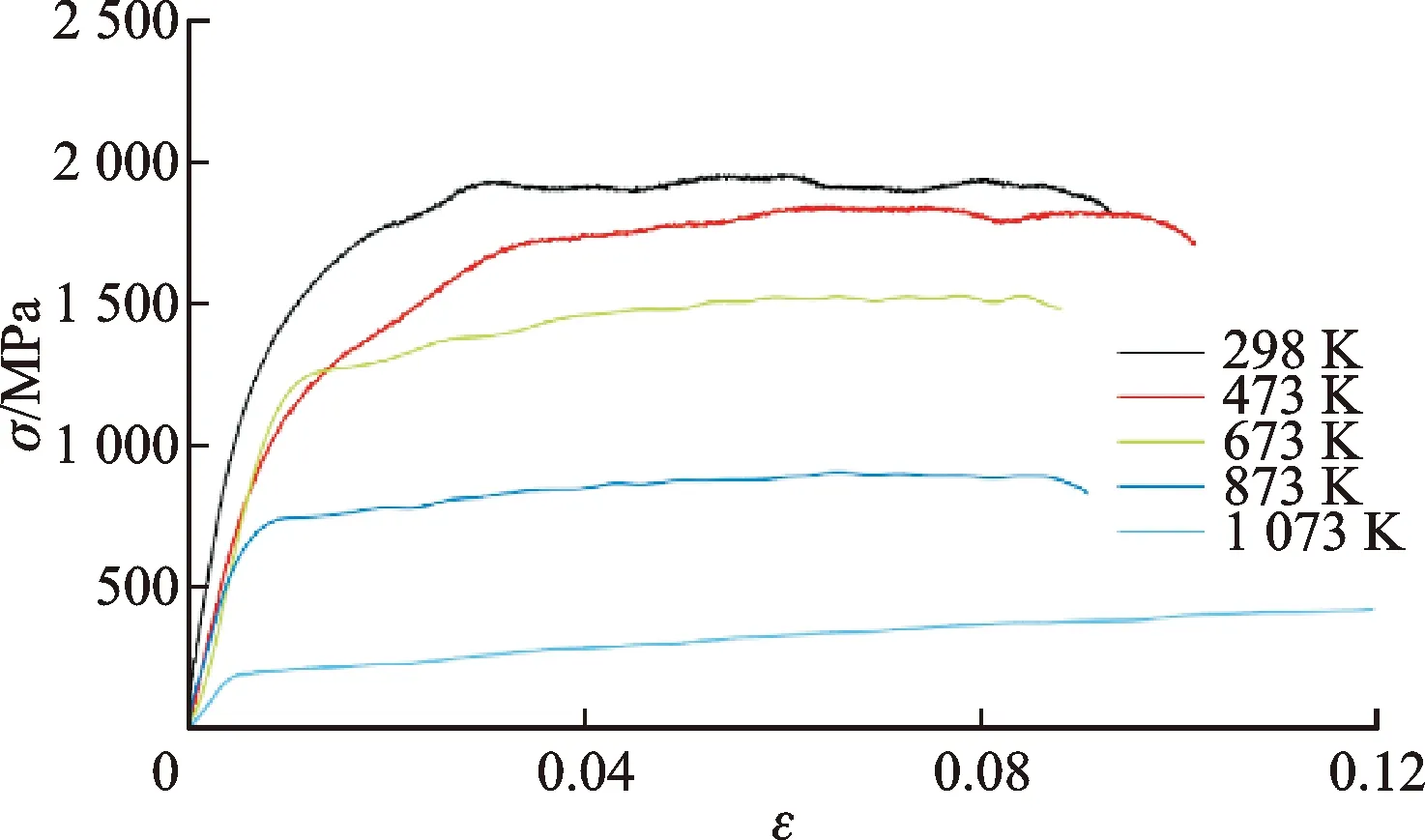
(a)应变率为800 s-1
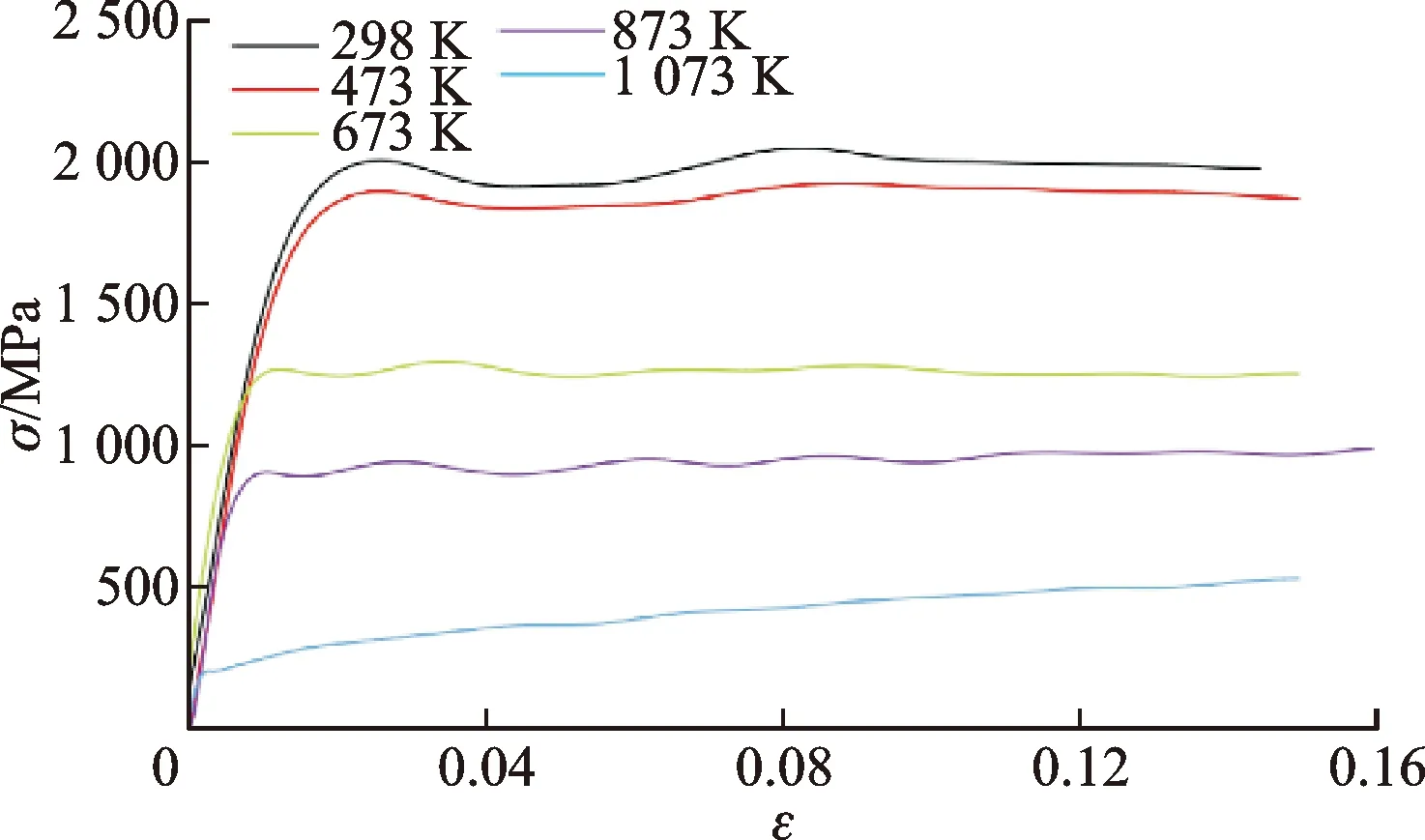
(b)应变率为3 000 s-1
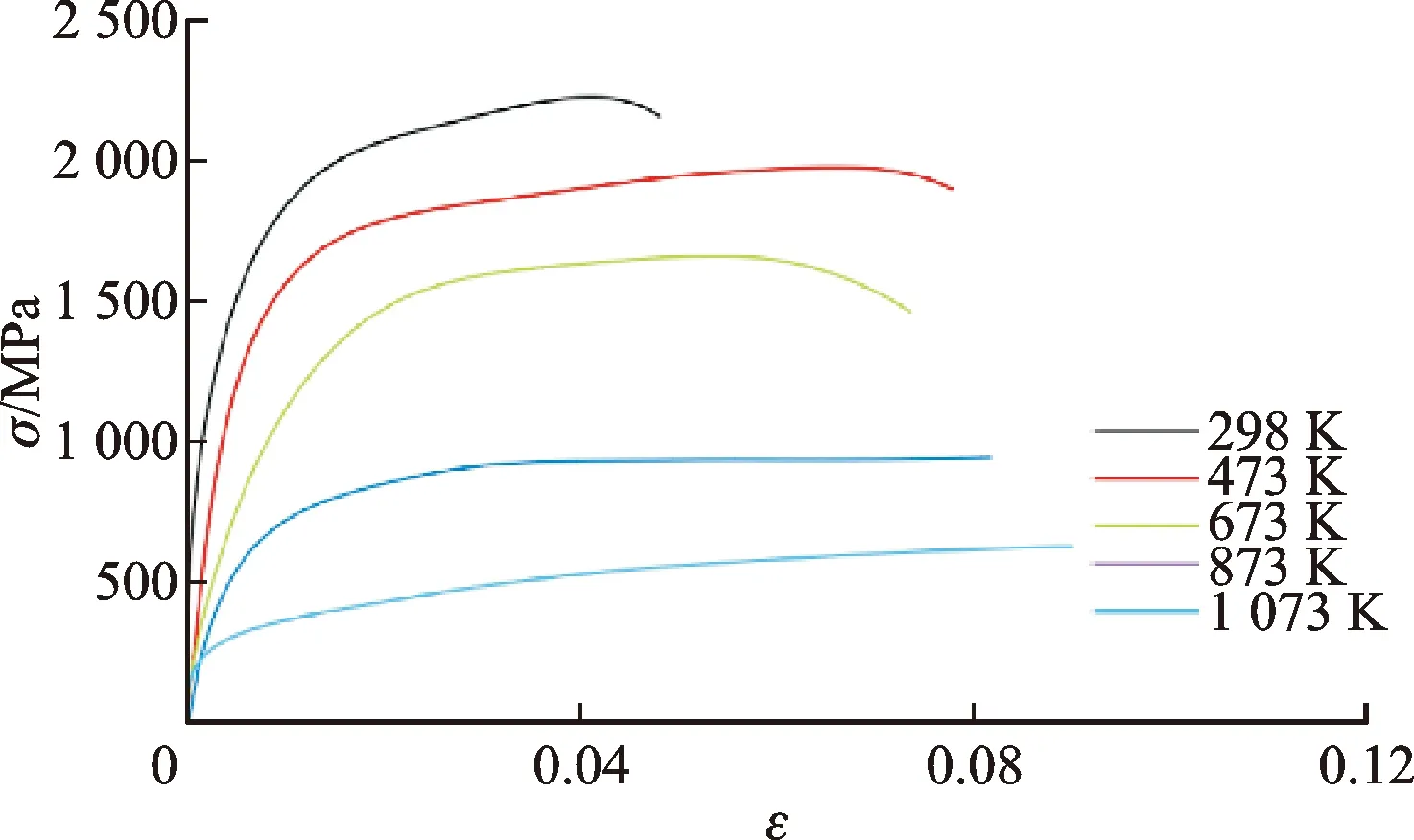
(c)应变率为10 000 s-1
通过图4所示的25 ℃和0.001 s-1应变率下的真实应力-应变曲线拟合确定参数A、B和无量纲参数n,通过图6所示的25 ℃初始温度时不同应变率下的真实应力-应变曲线拟合得到无量纲参数C。利用恒定应变率不同温度条件下的真实应力-应变曲线拟合得到无量纲参数m。经过试验分析获取的Johnson-Cook模型参数见表1。
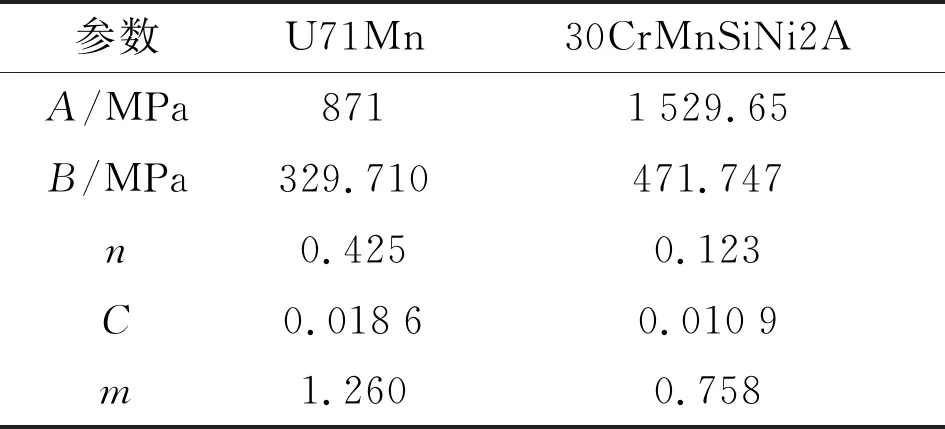
表1 Johnson-Cook本构模型参数
2.2 基于绝热剪切理论的靴轨材料失稳条件
基于绝热剪切理论,国内外学者进行了大量材料失稳研究。包合胜等[26]基于Johnson-Cook热黏塑性本构模型,认为绝热剪切的临界条件同时取决于应变、应变率和环境温度3个因素,推导出了与三因素相关的三变量准则,用此三变量临界准则进行理论预测,验证与试验结果吻合较好。Johnson-Cook热黏塑性本构方程如下
τ=
(2)

(3)
以式(2)、(3)为基础,在其中代入相应的假设条件,如滑靴侵彻速度恒定、应变率恒定、功热1∶1转换等,最终得到靴轨高速撞击形成刨削时的材料失稳条件如下
[ρCv(Tm-Tγ)]-1=0
(4)
2.3 MPM物质点分析方法
刨削是一个复杂的材料破坏问题,其复杂性体现在:①刨削过程涉及材料的大变形和塑性流动,应力、应变关系为强非线性;②靴轨刨削接触核心区域应变率可高达107s-1,导致应力激波的产生与传播;③高应变率引起材料的大范围温度变化,导致金属材料的固液态甚至包括气态相变;④塑性流动射流引起滑靴材料与轨道材料的相互混合以及产生空穴。基于拉格朗日的有限元法,无法处理这种混合和空穴,基于欧拉描述方法,由于存在数值扩散问题,无法精确计算对流项。
物质点法采用拉格朗日质点和欧拉网格双重描述,将连续体离散成一系列携带所有信息的连续质点。物质点法示意图如图7所示。背景网格仅用于动量方程的求解和空间导数的计算,之后再将运动信息映射回物质点,得到下一时刻物质点所携带的物质信息。在每步中物质点和网格结点一同变形,没有相对运动,因此避免了欧拉法中因非线性对流项产生的数值困难,并容易跟踪物质界面。在下一时间步中,抛弃变形后的背景网格,仍采用未变形的背景网格,物质信息被映射回网格结点,从而避免了拉格朗日法中因网格畸变而产生的数值困难[16]。

图7 物质点法示意图Fig.7 Diagram of material point method
采用物质点方法,对刨削问题进行数值模拟,遵循质量守恒、动量守恒、能量守恒理论,公式如下
ρ(X,t)J(X,t)=ρ0(X)
(5)
(6)
(7)
3 基于在轨试验结果的刨削仿真分析
3.1 刨削试验现象分析
(1)化学成分分析。选取上述试验中如图3所示的滑轨踏面某典型刨削坑(尺寸约220 mm×18 mm)为样本进行分析,化学成分检测结果见表2。检测结果表明,钢轨的化学成分符合YB/T 5055—1993《起重机用钢轨》标准中对U71Mn钢轨成分的要求。同时,样本中还检测出了Cr的成分,这与滑靴材质30CrMnSiNi2A成分是相符的,证明刨削过程中,部分滑靴材料熔融后附着在滑轨上(检测前采用化学试剂对样本进行了清洗,排除滑轨表面因滑动摩擦附着滑靴材料的可能)。
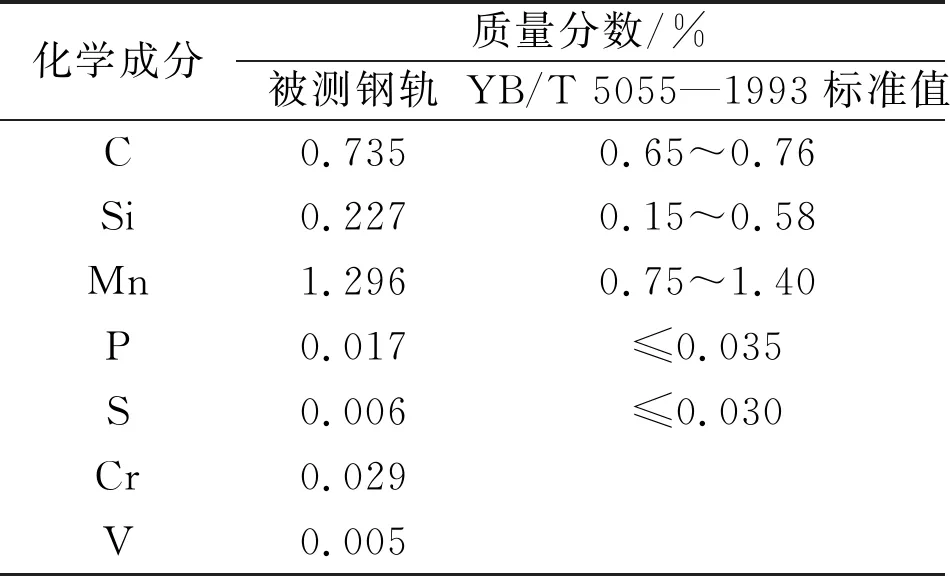
表2 试验用U71Mn钢轨与标准化学成分对比
(2)金相显微组织检测。刨削的形成涉及高压、高速和高温的复杂作用,难以找出符合这一现象的力学参量去描述。研究刨削发生后轨道刨削坑周围的微观结构、刨削坑内微观组织的变化是研究刨削过程的重要手段。在钢轨上取金相试样,取样位置和宏观形貌如图8所示。

(a)取样位置

(b)试样宏观形貌
金相取样微观结构如图9所示,其中图9(a)为2-2试样纵向200 μm尺度下的磨面金相图。因滑靴对滑轨的冲击和摩擦作用,导致试样表面形成一层白亮组织,这是钢轨局部在冷态下遭受滑靴摩擦热和冲击热温度骤升,珠光体向奥氏体转变,同时因钢轨本体迅速传热令奥氏体极冷淬火形成的马氏体组织。白亮组织层下方可见明显塑性变形,塑性变形厚度约为338 μm;并且可以观察到与橇体运行反方向成约45°夹角的绝热剪切带。

(a)纵向磨面

(b)横向磨面
图9(b)为2-3试样横向磨面金相图,从图中可明显看出沿绝热剪切带处有裂纹形成。这是由于在绝热剪切带内产生了很大的剪应变,而且应变率、温升均很高,周围存在大量相对“较冷”的基体,因剪切带内大、外小的不协调变形,不一致的应变率,急剧变化且不均匀的温度,极易在剪切带的边缘处产生微裂纹。随着剪切带的延伸,这些微裂纹急剧扩展和交叉,最后形成碎块脱落。正是绝热带中形成的裂纹,将滑轨表面分割成若干块,才使滑轨表面材料不断脱落,形成了刨削坑。因此,可使用绝热剪切理论来描述刨削效应。
3.2 刨削效应仿真
(1)仿真模型。基于物质点方法对火箭橇靴轨刨削过程进行数值模拟。为了更好地进行机理研究,需要对火箭橇靴轨进行合理简化。以某型火箭橇试验为研究对象,将发生刨削的火箭橇模型进行简化,建立滑靴与轨道模型如图10所示,滑轨材质为U71Mn,橇体与滑靴按质量分配关系简化为质量块,材质为30CrMnSiNi2A。
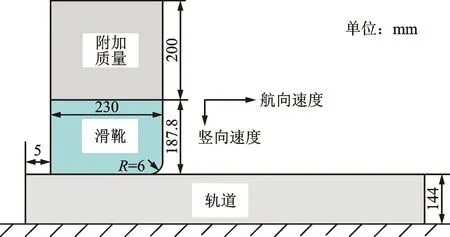
图10 滑靴与轨道几何模型Fig.10 Geometric model of slipper and track
模型中并非平直滑轨,而是根据试验时使用滑轨的真实不平顺特性建模得到的。滑轨不平顺特性如图11所示。

图11 火箭橇滑轨不平顺特性曲线Fig.11 Irregularity characteristic curve of rocket sled track
除此之外,仿真时还需要代入火箭橇航向速度、滑靴垂向速度、滑靴-轨道界面的正压力、气动加热与摩擦热等影响因素。航向速度取刨削发生处的实测速度,垂向速度分别代入1.75、2.00和2.25 m/s,正压力代入该滑靴承担的载荷分量与垂向振动值的乘积,气动加热与摩擦热代入复算值(气动热复算值通过气动热仿真获得,并经温度、热流测试数据校正;摩擦热复算值利用销盘试验结合有限元仿真获得,并经滑靴内腔梯度安装的温度传感器测试数据校正)。
(2)仿真结果。仿真过程中不考虑靴轨材料熔融现象,轨道下端固支,其余方向自由。轨道及滑靴离散的物质点间距为0.5 mm,背景网格间距为1 mm。仿真过程如图12所示。

(a)1.75 m/s

(b)2.00 m/s

(c)2.25 m/s
在二维刨削数值分析中,通常以刨削坑的深度作为试验与仿真一致性对比指标[16]。不同垂向速度刨削仿真结果如下:
(1)当侧向速度为1.75 m/s时,刨削坑的长度为169 mm,深度为1.51 mm;
(2)当侧向速度为2.00 m/s时,刨削坑的长度为224 mm,深度为1.73 mm;
(3)当侧向速度为2.25 m/s时,刨削坑的长度为264 mm,深度为2.05 mm。
垂向速度为2.00 m/s时刨削温度分析结果如图13所示。

(a)0.028 s时

(b)0.07 s时

(c)0.14 s时

(d)0.35 s时
在0.028 s时,靴轨接触面温度分布较为均匀,刨削头(沿速度方向刨削的最前端)位置温度相对偏高;在0.07 s时,靴轨接触面温升区域厚度增加,且高温层偏向滑靴一侧,最高温度可达到1 500 K,刨削头相对滑靴位置后移;在0.14 s时,高温层持续增厚,刨削头位于滑靴中间位置附近,温升区域呈扩张状态(与火箭橇运行方向相反),开始形成熔融溅射物;在0.35 s时,刨削坑完全形成,表面温度约为1 000 K,高温区域主要集中在滑靴配合面,最高温度为1 500 K,滑靴后方形成大量熔融溅射物。
3.3 试验与仿真结果对比分析
仿真结果与试验刨削现象参数对比见表3。由分析可知,当侧向速度由1.75 m/s增大到2.25 m/s时,刨削的深度逐渐增大,这一结论符合客观认知。3种工况数值仿真中,垂向速度为2 m/s时,偏差刨削效应仿真得到的刨削坑深度试验结果具有较好的一致性,试验与仿真偏差未超过5%。同时,2 m/s的垂向速度也与火箭橇设计经验值相一致。

表3 火箭橇刨削试验与仿真的对比
4 结 论
刨削效应是高超声速火箭橇试验的一种伴生现象,发生规律与靴轨材料属性、运行速度、滑靴间隙、滑轨表面质量等诸多因素相关[25-27],具有一定的随机性。本文通过研究试验中出现的刨削现象,得到以下结论。
(1)对真实试验刨削坑开展化学成分分析和金相显微组织检测,实现了闭环验证,验证了基于绝热剪切理论的刨削形成机理。
(2)选用了目前普遍使用的物质点方法进行刨削效应仿真,仿真加载参数全部来源于实测数据或有理论支撑的仿真数据,数据可溯源,验证了物质点法对刨削分析的适用性。
(3)分析复现了刨削形貌,得到了滑靴重要部件承力位置的温度分布(可用于滑靴结构安全性校核)。试验和仿真对比结果显示,当滑靴垂向速度为2 m/s时,刨削坑长度、深度偏差分别为1.8%、-3.9%,均未超过5%,具有较高的一致性,分析数据可以为后续高超声速火箭橇试验试前刨削评估提供参考与指导。
未来随着国内高超声速火箭橇试验量增加、试验数据的不断丰富,上述仿真模型和参数将持续得到优化,并最终形成标准规范、具有高置信水平的刨削效应分析方法。

