液氢中空气溶解度预测及氮-氧存在模式研究
梁鸽,王磊,上官石,雷刚,陈强,文键,厉彦忠
(1. 西安交通大学制冷与低温工程系,710049,西安;2. 航天低温推进剂技术国家重点实验室,100028,北京)
液氢具有能量密度大、储氢密度高等优势,在航天和储能领域日益重要[1-2]。液氢储运过程中,不可避免地存在少量空气渗入。空气主要成分氮、氧在液氢中的溶解度极低,会积累形成固空或固氧。研究表明,液氢中积累的固空呈现“外部富氧、中心贫氧”的分布特征[3]。当固空的表面氧分数较高时,液氢系统存在爆炸或爆轰风险[4-5],国内外已发生多起因固空导致的爆炸事故[6-10]。为避免固空大量沉积,需要对液氢系统的氮氧含量进行控制,明确空气在液氢中的最大溶解量及溶解规律。
目前,液氢中的固空特性研究尚不充分。早期研究多为爆炸实验所得经验性结论[6-13],主要探究了产生爆炸的固空氧含量阈值、爆炸原因及防爆措施。近几年,部分学者开展了固空在液氢中积累特性的理论和实验研究。在理论层面,有学者从氮氧体系的分子层面描述了氮氧浓度分布[3],也有学者采用元胞自动机与格子Boltzmann相结合的方法研究了固空晶体凝固和枝晶生长形貌变化[14-15]。在实验层面,北京航天试验技术研究所通过掺杂-复温的方法获得了初步的固空沉积规律[4-5]。然而,空气在低温液氢中的溶解规律鲜有报道,仅见20世纪关于氮气在液氢中溶解度的实验结果[16-17],理论方面鲜有文献报道。溶解度的计算实质是固液相平衡问题。在低温固液相平衡理论方面,已有溶液法[18-24]、状态方程法[25-30]、基团贡献法[31]等模型,但现有研究仍存在较大局限,很多方法依赖对实验数据的修正。此外,溶液法在20世纪提出并用于固液相平衡求解以来,陆续发展出理想溶液法[20]、正规溶液法(SH模型)[19]和改进的正规溶液法(MSH模型)等,并建立了一套预测固体在低温溶剂中溶解度的热力学框架[18]。其中,SH模型可在脱离固液相平衡实验数据的条件下预测二元体系的溶解规律,被多数学者采纳与应用。
本文以液氢-空气系统为研究对象,通过理论分析与模型修正实现氮气、氧气溶解度的计算预示,着重解决现有理论模型在液氢体系中预测偏差,通过重构溶解度参数,实现溶解度精确求解。在此基础上,对比不同介质在液氢体系中的溶解规律,获得空气的溶解极限,分析氮气、氧气在液氢中的存在模式与溶解边界,从而为液氢系统的安全防范与杂质控制提供理论指导。
1 空气溶解度模型
以N2-H2二元系统为例,溶剂标记为1,溶质标记为2。在计算温区内,固相为纯氮,液相为氮-氢二元混合液。根据固-液二元系达到相平衡时逸度相等,可以推导固体杂质在低温液体中溶解度,根据Preton和Prausnitz[18]的分析可知,当有固-固晶相转变[32]时,需添加转变焓予以修正
(1)

由式(1)可知,求得活度系数即可获取固相在二元液相中的溶解度,而活度系数可基于不同的溶液模型确定。
1.1 SH模型
SH模型也称正规溶液理论。当溶液中一个组分由理想溶液迁移到真实溶液时,若无熵和体积变化,则可称该溶液为正规溶液。
对于SH模型,混合液相中组分2的活度系数为

(2)
式中:V2为过冷液氮的摩尔体积;δ为溶解度参数;Φ1为液相中液氢的体积分数,计算式为
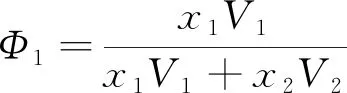
(3)
由于液氢中氮的体积分数极小,故可假设Φ1=1。
溶解度参数可由完全蒸发能和液体体积确定
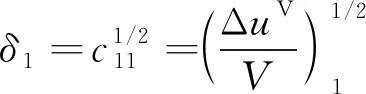
(4)
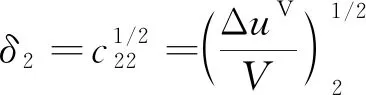
(5)
式中:ΔuV表示完全蒸发能,其物理意义是在温度一定时,饱和液体蒸发到理想气体(体积无穷大)的能量变化;c11为溶剂分子间的内聚能密度;c22为溶质分子间的内聚能密度。
对于非极性或弱极性分子,正规溶液理论中分子间作用力主要为色散力,内聚能密度间的关系可使用London公式[33]表示
c12=(c11c22)1/2
(6)
式中c12为溶质溶剂分子间的内聚能密度。SH模型适用于含有非极性或弱极性物质的混合物。
溶剂液氢的摩尔体积为
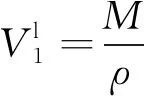
(7)
溶解度参数的估算关系式[34]为
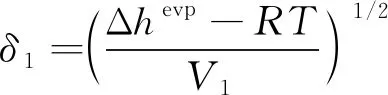
(8)
式中:Δhevp为液体摩尔蒸发焓;V1为液体摩尔体积。
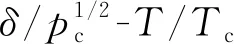
本文采用3次多项式拟合二者关系,可建立各溶质摩尔体积Vl和溶解度参数δ间的关系
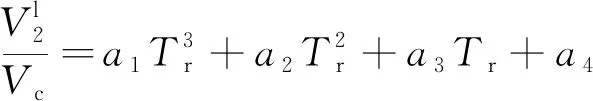
(9)

(10)
式中:Tr=T/Tc;Tc、pc、Vc分别为各溶质的临界温度、临界压力和临界摩尔体积;a、b为拟合多项式的系数。表1提供了不同溶质拟合参数a、b的具体取值。图1展示了不同溶质摩尔体积与溶解度参数随Tr的变化关系。可以看出,摩尔体积V在临近临界状态时变化较为剧烈,溶解度参数δ则表现出较为平缓的下降趋势。

图1 溶质摩尔体积与溶解度参数随温度变化的曲线Fig.1 Extrapolation of molar volume and solubility parameters for four solutes

表1 溶解度参数计算式中的参数取值
1.2 MSH模型
SH模型计算不精确与几何平均假设有关,分子形状差别是造成偏离几何平均的主要原因。但是,SH模型中没有对分子形状的描述。有鉴于此,MSH模型提出了改进
c12=(1-l12)(c11c22)1/2
(11)
式中l12<1是由实验结果关联推导的经验常数,表征了溶质与溶剂分子间的相互作用。
活度系数转化为

(12)
2 溶解度模型修正
图2展示了氮气在液氢中溶解度随温度的变化规律,图中纵坐标x代表某溶质在液氢中的溶解度,以摩尔分数表示,后文同。可以看出,当采用SH模型时,溶解度随液氢温度升高先增大后减小,最高溶解度对应温度约为27.5 K,与实验数据存在明显偏差。进一步地,采用SH模型复现梁益涛等的H2O-O2体系[22]和沈淘淘的CO2-CH4体系[24]溶解度规律,发现SH模型同样给出了类似的非单调变化规律,如图3所示。由此可见,SH模型在预测溶解规律时存在偏差,不适用溶剂临界点附近的溶解度求解。
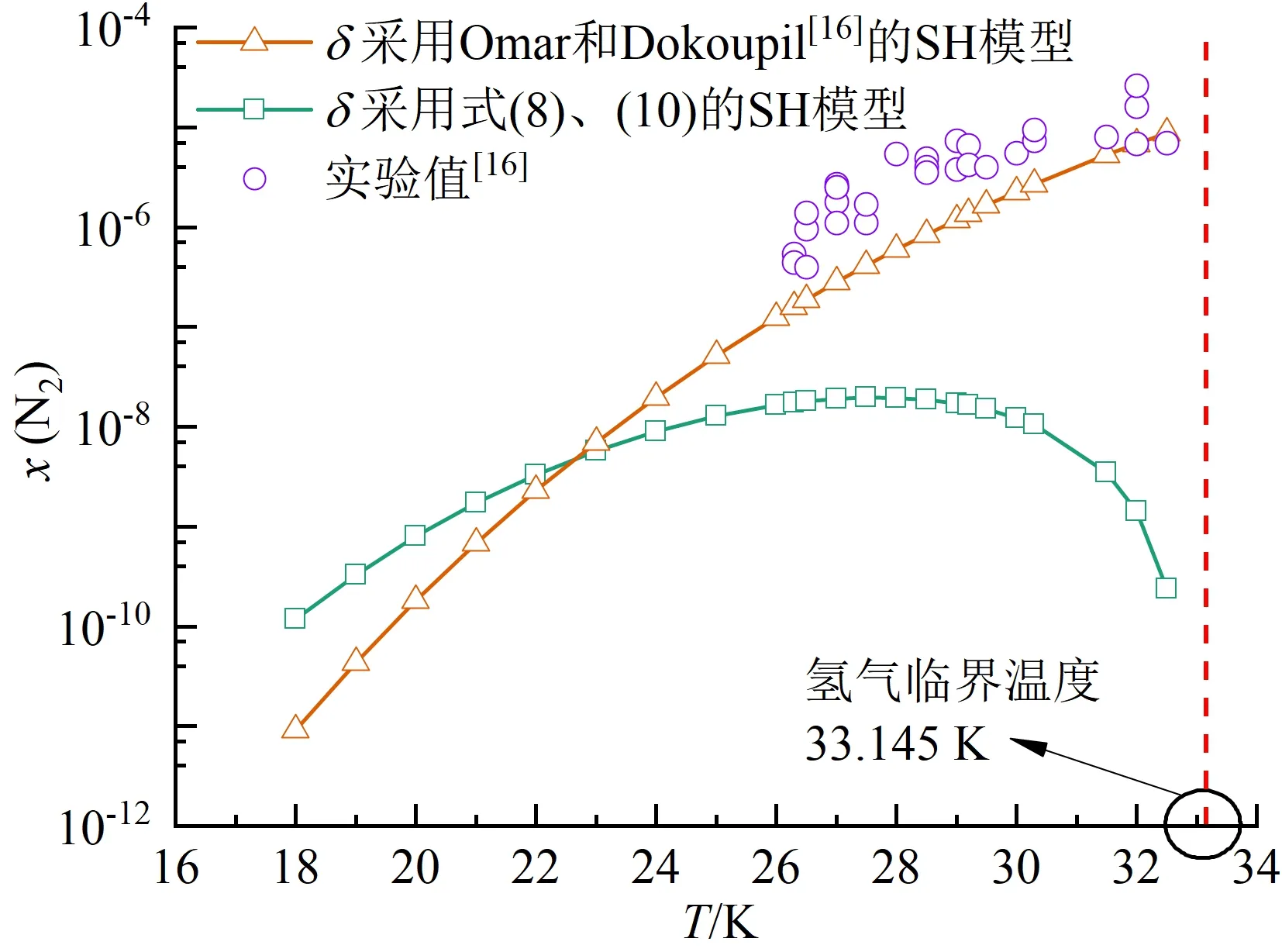
图2 SH模型采用不同δ的溶解度计算结果Fig.2 Solubility calculated by SH model with different δ

(a)H2O-O2体系[22] (b)CO2-CH4体系[24]图3 梁益涛等[22]和沈淘淘[24]的溶解度计算结果Fig.3 Solubility calculated by Liang Yitao[22] and Shen Taotao[24]
进一步分析可知,导致SH模型预测偏差的主要原因是溶剂溶解度参数δ1在靠近临界温度时取值不合理。本文利用Omar和Dokoupil[16]实验所得溶解度参数代入SH模型进行反推,发现不正确趋势得到较佳改善。实验数据反推参数见表2。可以看出,实验反推δ2-δ1随温度升高而降低,而SH模型中该值随温度升高而升高,最终导致结果异常。氮和氢的溶解度参数如图4所示。可以看出,在N2-H2系统中,溶剂氢的溶解度参数在温度接近临界点时变化剧烈,而实际上溶解度参数随温度的变化近似呈线性规律。因此,在液氢体系的溶解规律研究中,需对氢的溶解度参数进行修正。

表2 溶解度参数差δ2-δ1的实验反推值与模型求解值

图4 过冷液氮和饱和液氢的溶解度参数Fig.4 Solubility parameters of subcooled liquid nitrogen and saturated liquid hydrogen
导致溶剂液氢溶解度参数变化剧烈的根源在于其求解式在临界点附近的简化。根据前文,溶解度参数定义为式(4),式中ΔuV为液体完全蒸发能,等于1 mol饱和液体恒温下蒸发到理想气体所需内能。ΔuV由两部分组成,一部分是摩尔蒸发能Δul→g,指将1 mol液体蒸发至饱和蒸气所需内能,另一部分为Δug→∞,指饱和蒸气到无限大体积的理想气体所需内能,关系式如下
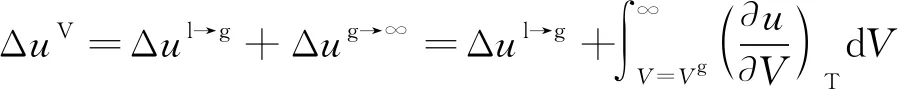
(13)
进一步展开为
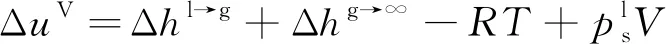
(14)
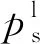

(15)
需要指出的是,临近溶剂临界点时,式(14)另外两项不能忽略,而前述模型及沈淘淘[24]和梁益涛等[22]的溶解度参数计算模型均使用了简化公式,导致临界状态附近的预测结果不合理。
Prausnitz[34]在关于SH模型的论述中提到,溶解度参数是温度的函数,但是溶质、溶剂的溶解度参数之差与温度弱相关,可假设
δ1-δ2=const
(16)
为了计算简便,可取溶剂熔点温度的溶剂和溶质溶解度参数之差|δ1(T1,m)-δ2(T1,m)|来确定其数值,δ1(T1,m)和δ2(T1,m)依然使用式(8)、(10)确定。
对于N2-H2系统,取液氢熔点13.96 K处饱和液氢、过冷液氮的溶解度参数之差,则氢的溶解度参数表示为
δ1=δ2+δ1(T1,m)-δ2(T1,m)
(17)
式中:δ1(T1,m)=5 523;δ2(T1,m)=15 559。
对于MSH模型,二元相互作用参数的选取须由实验数据确定。结合图2的实验数据,令氮气溶解度数据的平均相对误差(εave)最小,得l12=-0.093。
为便于分析,标记采用式(17)确定液氢溶解度参数的SH模型为SH*,标记l12=-0.093的MSH模型为MSH*。图5(a)展示了利用两种模型求解的18.0~32.5 K温区氮气在饱和液氢中的溶解度。可以看出,MSH*模型的预测结果与实验值吻合较好,其相对误差最高为26.5%,最低为0.73%,误差主要来源于常数l12在不同温度下的修正程度。SH*模型也能基本反映氮气在液氢中的溶解规律变化趋势,溶解度虽整体偏低,但精度相较传统SH模型已大为改善,可在较宽的温度范围内实现溶解度的预测。
进一步地,比较了两种方法的平均相对误差(εave)、最大相对误差(εmax)和平均百分误差(κ),定义式分别为
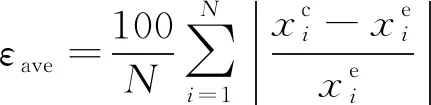
(18)
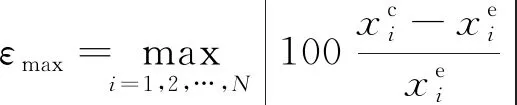
(19)
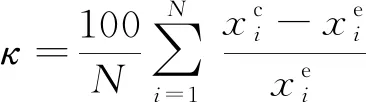
(20)
式中:xc为溶解度计算值;xe为溶解度实验值;N为数据点的总数。氮气在饱和液氢溶解度计算中的εave、εmax、κ如表3所示。可见看出,SH*模型各项误差较大,但可脱离实验数据的限制,MSH*模型的各项误差控制在20%以内。

表3 氮气在饱和液氢溶解度计算中的εave、εmax、κ
3 液氢中空气溶解度结果与分析
当采用溶液法求解溶解度时,一定温度、压力下的液氢密度ρ、液氢摩尔蒸发焓Δhevp均随温度T变化,具体取值可通过NIST[35]查询。本文计算温区为18.0~32.5 K,并将体系压力设定为液氢在该温度下的饱和压力,其余参数如表4所示。
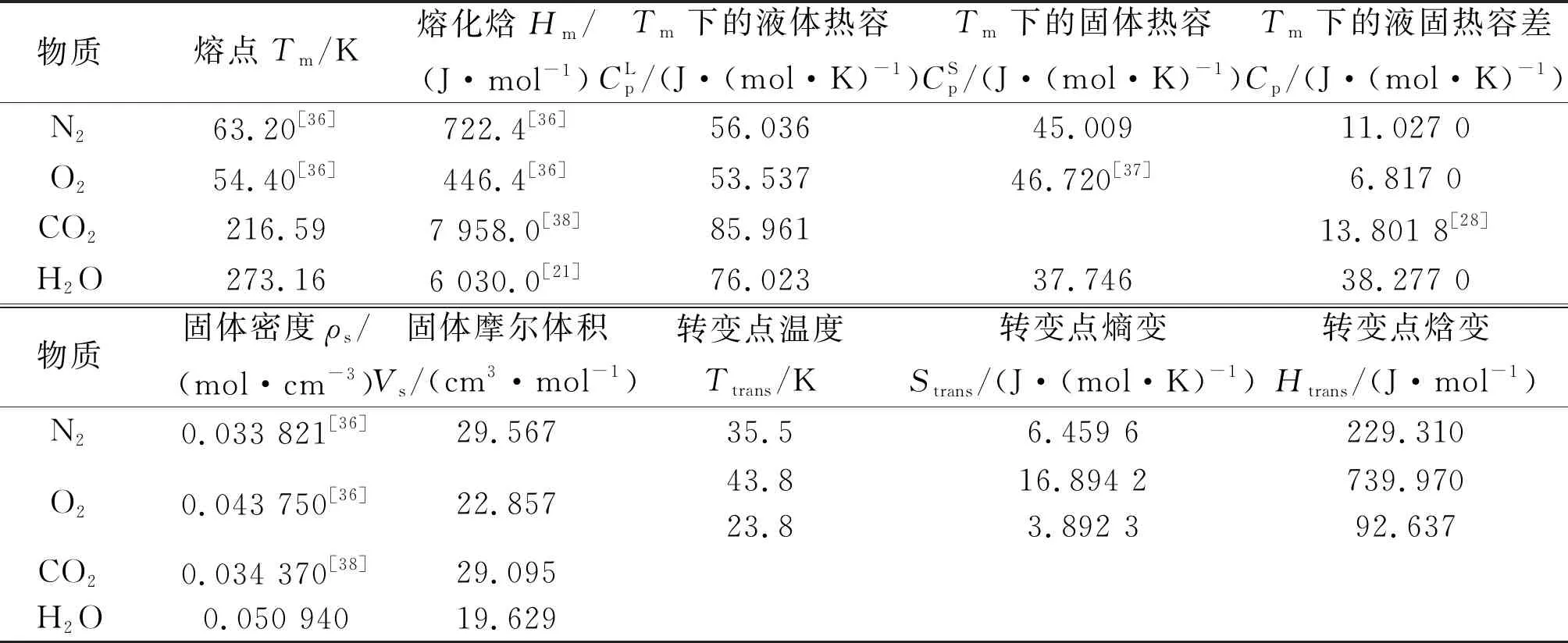
表4 物性参数
本文对比了氮气、氧气、二氧化碳和水在饱和液氢中的溶解度规律,由于O2-H2、CO2-H2和H2O-H2体系缺乏实验数据,溶解度预测时沿用了N2-H2系统的相关设置。4种溶质采用两种方法预测的溶解度规律如图5(a)~(d)所示。可以看出,4种溶质在液氢中的溶解度均随温度升高而增大。在同一温度下,SH*模型预测结果始终小于MSH*模型。

(a)氮气

(b)氧气
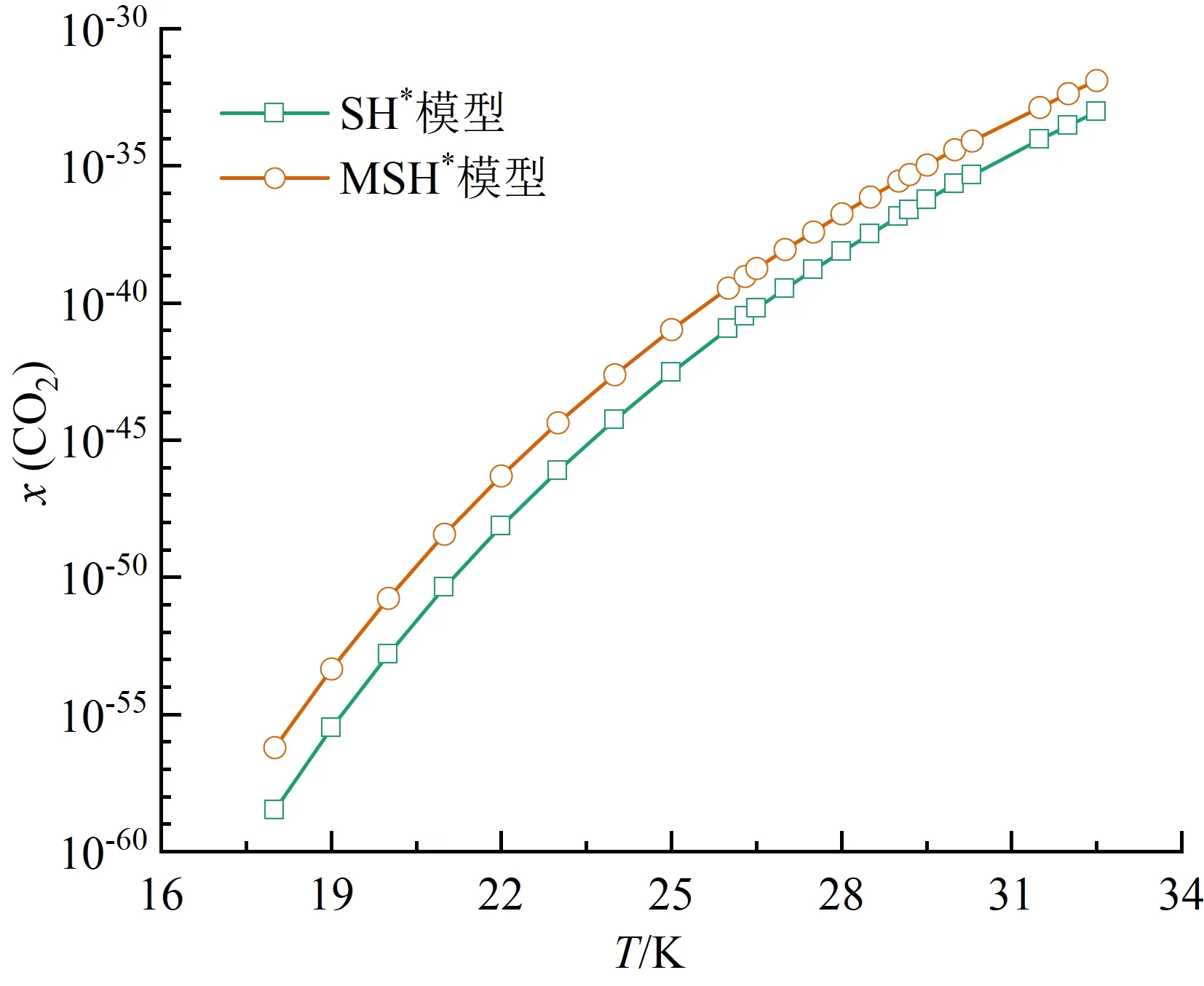
(c)二氧化碳
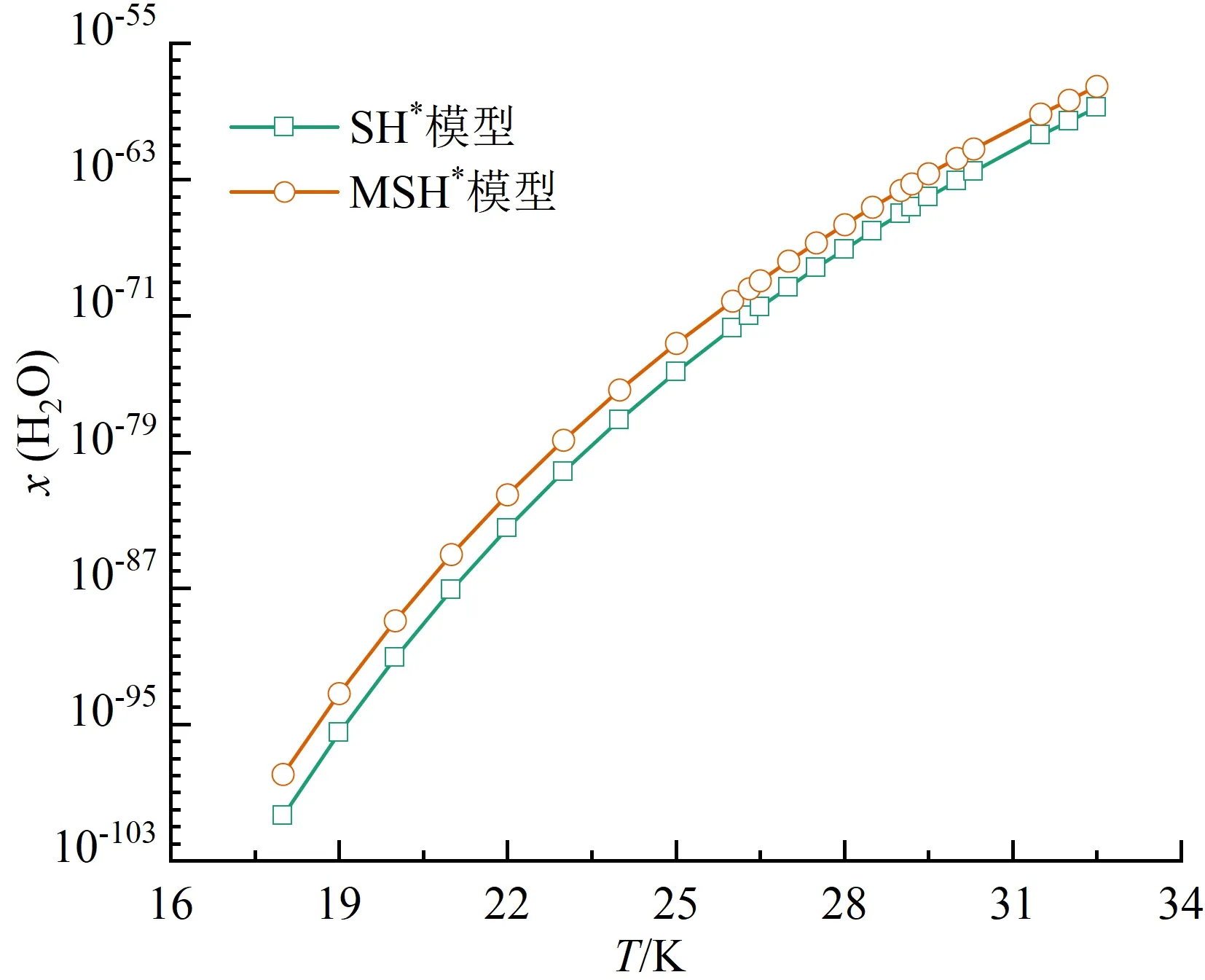
(d)水
对4种溶质的预测结果比较如图6所示。同一温度下:氮气的溶解度最大,在10-9~10-4之间;氧气的溶解度次之,在10-13~10-7之间;二氧化碳的溶解度更小,在10-57~10-31之间;水的溶解度最小,在10-98~10-56之间。从数量级来看,不同溶质对温度的敏感程度不同。在18.0~32.5 K,氮气的溶解度跨越了最少数量级,水的溶解度跨越了最多数量级。4种溶质的溶解度数据给出了各自在液氢中的溶解极限,超出该极限会凝结为固相杂质,造成液氢系统管路阻塞。由于二氧化碳与水的溶解度极小,微量泄露会形成固体颗粒,因此液氢系统中应尽可能脱除这两种杂质。

图6 MSH*模型下不同溶质的溶解度对比(摩尔分数)Fig.6 Comparison of solubility for different solutes calculated by MSH* model (mole fraction)
4 液氢中氮氧存在模式
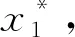
以20 K液氢为例,对图7所示规律开展进一步讨论。空气中氧气、氮气在该温度的溶解极限分别对应于图中的A点与B点。当空气漏入量超过A点对应数值时,氧气开始结晶析出。在空气漏入量达到B点之前,所析出的固体颗粒为纯固氧。随着空气漏入量超过B点后,空气中无法溶解的氮分子也开始结晶析出,固体颗粒中的平均含氧量逐渐减少,并随着空气漏入量的增加逐渐逼近空气中的固氧摩尔分数0.21。

图7 液氢中空气溶解极限及固相中氧摩尔分数Fig.7 The solubility limit of air in liquid hydrogen and the mole froution of oxygen in solid phase
固空中氧含量的占比与液氢-固空系统是否产生爆轰或爆炸密切相关。当氮氧分子以前述状态②存在于液氢时,固相中只存在氧,该固体颗粒在液氢系统的局部聚集时,极易发生安全事故。针对前述所介绍的状态③,所形成的固空中氮氧平均比例与空气中的比例近似统一,氧的平均浓度较低。但是,从已有报道看,空气的结晶过程并非是氮氧均匀结晶,而是氮先析出氧后析出,所形成的固空呈现氧包氮的特征,同样会形成富氧固空-液氢直接接触的危险状态。因此,严格控制液氢系统中的空气量对于液氢系统的安全设计具有重要意义。
液氢作为火箭推进剂与储氢载体,加注前须进行气体置换。气体置换首先使用纯度较高的氮气置换,当其他杂质含量低到一定程度后,再使用氦气置换。以上结论为液氢容器中氮气、氧气置换提供了设计依据。可以看出,氧气的置换标准较之氮更为严苛,若氧含量控制不佳,易在液氢系统中形成固氧或氧含量较高的固空。此外,温度越高,液氢可溶解更多空气,更不易形成固空,即采用过冷液氢更易发生固氧析出与聚集。因此,在液氢过冷系统中更应关注空气的泄漏量,并采用更高的气体置换标准。
5 结 论
本文针对空气在液氢中的溶解规律与存在模式开展了理论预测,主要结论如下。
(1)传统SH模型中,溶剂溶解度参数的简化导致该模型在靠近临界状态时表现出明显偏差。本文提出了一种溶解度参数的简化模型,可实现近临界温区溶解度的准确预示。通过实验数据的拟合分析,本文提出当二元相互作用参数l12=0.093时,MSH模型也可实现液氢中不同溶质溶解规律的准确预示,最小平均误差约12.52%。
(2)预测表明,对于18.0~32.5 K温区的液氢系统,氮、氧、二氧化碳、水的溶解度分别为10-8、10-12、10-51、10-89摩尔分数,因此二氧化碳与水极难溶于液氢中,液氢系统必须严格控制这两种组分的含量,避免该组分结晶所导致的堵塞风险。
(3)空气在液氢中存在模式随空气量增大而发生变化。当空气量极少时,氮、氧分子完全溶解,无固体颗粒产生;当空气量处于不生成固氧、固氮对应的空气溶解极限之间时,无法溶解的氧分子结晶析出,产生固氧颗粒;当空气量进一步增大时,氮氧分子均结晶析出,形成固空,且固空的平均组分随析出量的增大逐渐接近空气中氮氧比例。
(4)就液氢系统的安全运行而言,必须严格控制空气残存量与泄漏量,系统设计应以不生成固氧情况下的空气溶解极限为标准执行。

