抓住要点 把握内容 认识概率

文／胡永强

本章包括三节内容，分别是“确定事件和随机事件”“可能性的大小”“频率与概率”。这三节内容是按照递进关系呈现的，要想充分理解和把握本章内容，我们需要在学好这三节内容的基础上，弄清它们之间的逻辑关系。

一、事件及分类

生活中，在事情发生之前，有些事情是否会发生是确定的，有些事情是否会发生是不确定的。我们把确定的事情称为确定事件，确定事件包括必然事件和不可能事件；把不能确定是否发生的事件称作随机事件。必然事件指在一定条件下，一定发生的事件，如在全是空位的电影院里，小红找到一个空位；不可能事件是指在一定条件下，一定不发生的事件，如从一百件正品中找到一件次品；不确定事件即随机事件，是指在一定条件下，可能发生，也可能不发生的事件，如七个人排成一排照相，甲、乙正好相邻。

二、事件发生的可能性

“用数学的眼光观察现实世界，用数学的思维思考现实世界，用数学的语言表达现实世界”既是数学学习的出发点，也是数学学习的归宿。事件发生的可能性有大有小，如何用数学的语言描述它呢？在数学中，我们通常用0 和1 及其之间的数值来表示某一事件发生的可能性。不可能事件发生的可能性为0；必然事件发生的可能性是1；随机事件发生的可能性介于0和1 之间。一般地，随机事件发生的可能性有大有小，我们可以利用已经学过的相关数学知识计算它。

例1掷一枚正方体的骰子，各个面上分别标有数字1、2、3、4、5、6，求下列事件发生的可能性大小：（1）朝上的数字是奇数；（2）朝上的数字能被3除余1；（3）朝上的数字不是3 的倍数；（4）朝上的数字小于6。

三、用频率估计概率

一个事件发生的可能性大小的数值，就是这个事件发生的概率。随机事件发生的概率是由其自身决定的，是随机事件的自身属性，它反映这个随机事件发生的可能性的大小。有的随机事件发生的概率可以通过计算获得，有的随机事件发生的概率很难直接确定。对于难以直接确定概率的随机事件，我们可以采用间接方法获取，比如用多次重复试验下的“频率”估计“概率”。

例2在一个不透明的口袋里装有若干个相同的红球，为了估计袋中红球的数量，八（1）班学生在数学实验室分组做摸球试验：每组先将10 个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复。表1 是统计汇总这次活动各小组数据后获得的全班数据。请估计随机摸出一个球是白球的概率。

我们需要弄清频率与概率之间的关系。从表中的统计数据可知，在大量重复试验下，摸到白球的频率稳定在0.4左右，据此可以估计随机摸出一个球是白球的概率约为0.4。

总之，科学合理的数据往往比个人的主观判断更为可靠。研究随机事件的概率可以帮助人们做出科学合理的预测与决策，这很好地体现了数学和生活之间有着密切的联系。

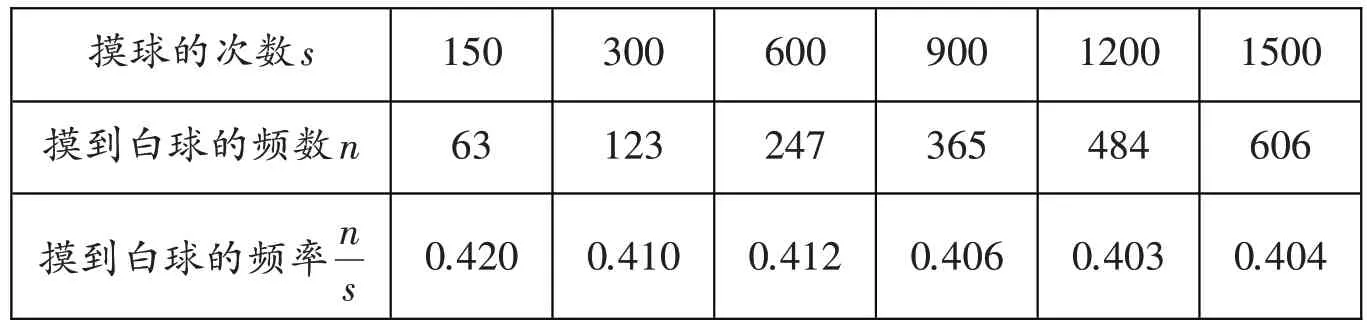
表1