基于RBF神经网络自适应滑模的机器鱼运动控制

王治平,李宗刚,陈引娟,杜亚江

(1.兰州交通大学机 电工程学院,兰州 730070;2.兰州交通大学 机器人研究所,兰州 730070)

0 引言

为了更好的开发利用水下资源以及对水下生物的生活习性进行观察研究,越来越多的自主水下机器人(AUV)被成功研发。相比于传统螺旋桨驱动的水下航行器,仿生机器鱼作为一种新型水下机器人,在水中作业时具有游动效率高、机动性能好、运动阻力小、隐身性能优良等优点[1-7]。由于水下工作环境的复杂性和任务的特殊性,仿生机器鱼在水下作业时往往需要灵活多变的三维运动以规避障碍物并完成预设任务。

近年来,对于仿生机器鱼的运动轨迹控制已经取得了一定的研究成果。Saurab Verma等[8]研发了无胸鳍,单自由度尾鳍的机器鱼样机,通过鲁棒自适应方法实现了机器鱼的转弯运动控制。Su等[9]在装有陀螺仪的三关节机器鱼上通过PID控制方法对机器鱼的转角进行控制。Li等[10]使用自适应学习算法对双连杆机器鱼的速度和转弯运动进行控制。Wu等[11]在具有四关节身体2自由度胸鳍以及可转动头部的机器鱼样机上,通过更改中央模式发生器(CPG)的参数,实现了机器鱼的直游、转弯、上浮下潜等运动模态。李宗刚等[12]团队设计了2自由度胸鳍与单关节尾鳍的仿生机器鱼,并对机器鱼的转弯特性进行了分析,通过实体实验验证了其理论的可行性。Wang等[13]利用线性二次调节(LQR)方法控制具有沉浮机构的机器鱼,实现了上浮下潜等水下三维运动。Wang等[14]控制具有单关节尾鳍与摇翼运动的机器鱼,实现了空间螺旋运动。相比于陆地环境,仿生机器鱼作业的水下环境中存在着复杂的流体运动等非线性扰动,难以建立精确的机器鱼水动力学模型。目前仿生机器鱼的运动控制大多停留在平面运动或俯仰运动范围[10,15-18],对于闭环三维运动控制问题尚未完全解决。同时研究者所开发的机器鱼样机大多是以单自由度或2自由度摆动的胸鳍,难以对真实鱼类的胸鳍运动进行模拟,降低了机器鱼运动的灵活性和机动性,限制了机器鱼的最小转弯半径等运动特征。

本文通过RBF神经网络与滑模控制算法相结合的方式控制机器鱼运动,并使其运动轨迹快速收敛至设定期望值。RBF神经网络具有学习规则简单,收敛速度快,泛化能力强的特点,且对任意非线性系统能进行有效逼近[19-22],所以采用RBF神经网络算法根据系统的误差信号对机器鱼动力学模型进行实时在线逼近修正。滑模控制算法具有简单、鲁棒性能好,可靠性高的特点,广泛应用于水下机器人控制[23-24]。为降低滑模控制所带来的抖振问题,本文采用饱和函数的方法实现控制器输出信号的连续切换,通过李雅普诺夫定理证明了机器鱼运动控制系统具有渐近稳定性,提高了机器鱼运动控制鲁棒性的同时拓宽了其作业场景。

针对以上问题,本文设计制作了具有3自由度胸鳍以及三关节尾鳍的仿生机器鱼样机。通过分析其运动机理构建了机器鱼的水动力学模型,并采用RBF神经网络控制与滑模控制相结合的算法。通过系统的仿真数学模型,对机器鱼三维空间运动轨迹的跟踪效果进行了仿真验证,同时使用仿生机器鱼样机进行螺旋下潜运动的实体实验,进一步验证了本文所述方法的有效性。

1 仿生机器鱼动力学模型

1.1 推进机构运动学建模

通过对鱼类胸鳍运动的观察分析[25],设定刚性3自由度胸鳍高效摆动规律方程为

θ1=-A1cos(2πf1t+φ)+θ1a

θ2=-A2cos(2πf2t)+θ2a

θ3=-A3cos(2πf3t)+θ3a

(1)

式中:fi(i=1,2,3)为频率;φ为前后与上下拍翼的相位差;θ1、A1、θ1a为前后拍翼的角位移、幅值、偏置;θ2、A2、θ2a为上下拍翼的角位移、幅值、偏置;θ3、A3、θ3a为摇翼的角位移、幅值、偏置。

根据螺旋运动规律可知,取式(1)中A1=π/4,A2=π/8,A3=π/2,θ1a=θ2a=θ3a=0,得胸鳍摆动轨迹曲线如图1所示,仿生机器鱼在此运动规律下,可产生前进运动和俯仰运动的推力分量。

图1 胸鳍摆动轨迹曲线Fig.1 Pectoral fin swing trajectory curve

1.2 推进机构动力学分析

仿生机器鱼在水中受力为胸鳍后摆推进力、回程阻力、形体阻力以及附加质量力等。推进力主要由胸鳍摆动和尾鳍摆动产生,其中利用3自由度胸鳍摆动可以实现机器鱼水平面的前进与垂直面的俯仰运动,利用尾鳍摆动时的偏置可实现机器鱼的转弯运动。

1) 胸鳍推进动力学分析。根据胸鳍运动学模型,通过理论力学中“微元积分法”对胸鳍进行受力分析[26],可得胸鳍推进方程为

(2)

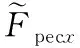
2) 尾鳍推进动力学分析。根据三关节尾鳍摆动规律,对x方向推进力分析[27]可得:

Ftail=2πρS(fh0)2sin(2πft)cos[α0cos(2πft-γ)]

{2πsin(2πft)-tan[α0cos(2πft-γ)]/St′}

(3)

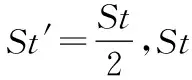
3) 胸/尾鳍协同推进动力学分析。当φ∈(0,π/2)时,胸鳍摆动可产生x和z轴正方向推力分量,调节φ的取值,使其在垂直方向实现俯仰运动。其胸鳍推进力为

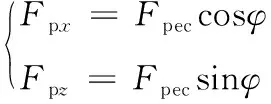
(4)

当尾鳍以偏置β摆动时,将为机器鱼运动提供y方向的侧向力,实现其转弯运动行为。此时机器鱼尾鳍推力为

(5)

综合式(2)—式(5),仿生机器鱼螺旋运动动力学方程为

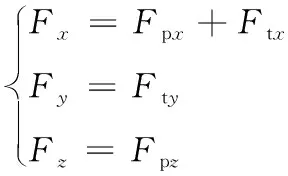
(6)

其中,Fx,Fy,Fz分别是机器鱼x,y,z方向所受的合外力。

1.3 仿生机器鱼动力学建模

仿生机器鱼在水中运动时,受到各个方向的力和力矩,建立动力学模型[28]如下:

(7)

式(7)中:

M=MRB+MA

C(υ)=CRB(υ)+CA(υ)

D(υ)=D(υ)+Dn(υ)

其中:η=[x,y,z,φ,θ,ψ]T表示机器鱼运动位姿,υ=[u,v,w,p,q,r]T表示机器鱼运动速度,J(η)表示转换矩阵,形式见文献[28];MRB表示刚体质量及惯量矩阵;MA为附加质量矩阵;CA(υ)为附加质量引起的类科里奥利/向心力矩阵;CRB(υ)为机器鱼质量引起的科里奥利/向心力矩阵;D为线性阻尼矩阵;Dn(υ)为非线性阻尼矩阵;g(η)是机器鱼位置和姿态有关的恢复力(力矩);τ为机器鱼受到的推力(力矩),由式(6)可得;τE包含机器鱼受到由风、浪和流等环境干扰力引起的力(力矩)。

2 仿生机器鱼控制器设计

本文在所构建的机器鱼水动力学模型基础上,采用RBF神经网络控制器对机器鱼动力学模型的不确定项和水流干扰项在线逼近,并采用滑模控制其趋近速度和精度。RBF神经网络自适应滑模控制器架构如图2所示。

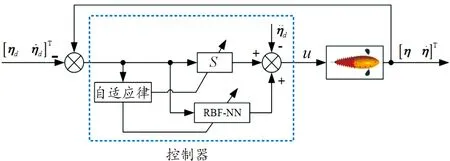
图2 RBF神经网络自适应滑模控制器架构Fig.2 RBF neural network adaptive sliding mode controller architecture

2.1 控制律设计

(8)

式中,e1、e2分别为运动轨迹误差、轨迹误差变化率。

根据式(7)和式(8),可建立如下所示描述状态空间的非线性不确定系统:

(9)

式(9)中:

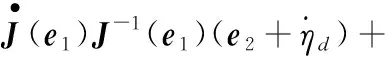
d(e,v)=-J(e1)M-1τd

u=J(e1)M-1τ

2.1.1神经网络逼近模型不确定项和环境干扰

由于机器鱼实际运动中,式(9)中的不确定项为模型的不确定项f(e,v)和水流及环境干扰d(e,v)。因此,本文通过神经网络算法对不确定项进行在线逼近,从而减少动力学模型的误差。将不确定项定义为

F(e,v)=f(e,v)+d(e,v)

(10)

由RBF神经网络算法原理,可知

F(e,v)=W*Th(e)+ε

(11)

式中,h(e)=exp(-(e-m)2/σ2),h(e)为隐含层输出,e为隐含层输入;W*为最优权值。

在机器鱼实际运动中,根据式(10)和式(11)得未知项逼近:

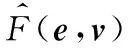
2.1.2滑模控制面设计

设计滑模面

S=e2+Ce1

(13)

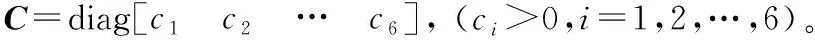
则

(14)

将本文的非线性系统(式(9))代入式(14)可得:

(15)

为了减少速度输出存在抖动,本文使用饱和函数sat(S),因此选择的趋近律为

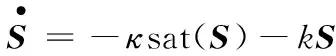
2.1.3滑模控制律和自适应控制律设计

(16)

(17)

(18)

其中,λ和γ均为正常数。

2.2 稳定性证明

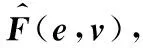
(19)

对于自适应滑模控制律和自适应律,本文使用Lyapunov函数分析控制器的稳定性。

定义Lyapunov函数为

V(t)=V1(t)+V2(t)+V3(t)

(20)

对式(20)求导可得

(21)

其中

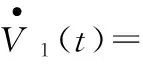
故而

(22)

将自适应律式(17)和式(18),代入式(22)得

(23)

3 仿生机器鱼螺旋运动模态分析

在螺旋运动的仿真实验中,设定机器鱼的期望轨迹为空间螺旋线,其运动方程为

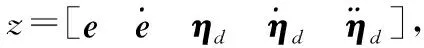
称取八角枫药材适量，烘干、磨粉，加水1 000 mL煎煮3 h，滤过；再加水600 mL煎煮2 h，滤过；合并两次滤液，浓缩，得质量浓度为1 g/mL（按生药量计）的八角枫水提液。

通过Matlab/Simulink运行仿真程序,得到机器鱼x,y,z方向位置和姿态角位移曲线如图3所示,可知机器鱼在运动初始阶段与期望轨迹有偏差,在1 s以后其运动轨迹和期望轨迹基本重合,轨迹跟踪效果显著。

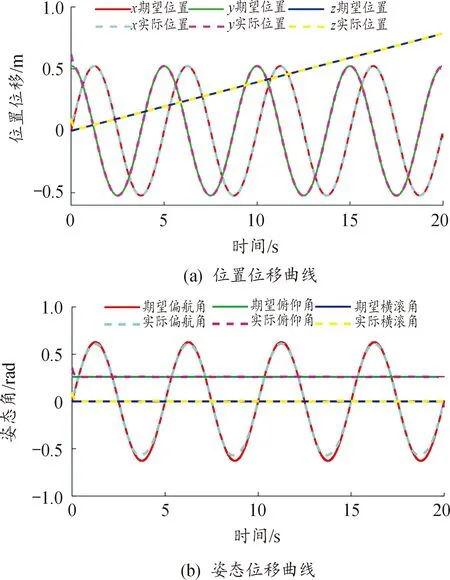
图3 机器鱼位置和姿态位移曲线Fig.3 Robotic fish position and attitude displacement curves

通过将x、y、z三个方向的位移曲线进行空间叠加,可得到机器鱼螺旋运动空间位移曲线如图4所示。

图4 机器鱼螺旋运动空间位移曲线Fig.4 The spatial displacement curve of the spiral motion of the robotic fish

由图4可得,机器鱼的实际运动轨迹和期望运动轨迹基本吻合,仅在运动初始阶段存在一定的位置误差。该现象发生的原因主要在于螺旋运动开始时机器鱼的位姿和期望位姿差异较大,执行器的快速动作破坏了原有稳定的水下环境,随后在控制器的作用下该位置误差得到了快速收敛。同时得到机器鱼各轴向速度及角速度的实时跟踪曲线如图5所示。

图5 机器鱼螺旋运动速度跟踪曲线Fig.5 Robotic fish spiral movement speed tracking curve

图5中(a)为x、y、z三个方向的线速度曲线,图5(b)分别为绕x、y、z三个轴的角速度曲线。由图可知,机器鱼的线速度和角速度在螺旋运动开始约0.5 s以后与期望值相吻合。同时速度和角速度曲线过渡平滑无尖点,运动开始时速度的跳跃突变也印证了位置误差出现的原因。

图6展示了机器鱼运动过程中实际位置和期望位置的误差曲线。

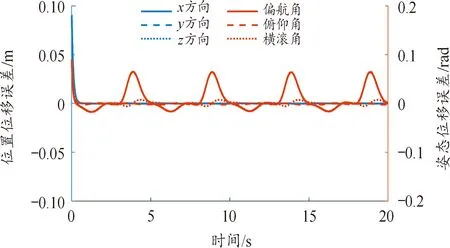
图6 机器鱼螺旋运动位姿误差曲线Fig.6 The spiral motion position error curve of robotic fish

由图6可知,机器鱼的轨迹误差始终保持在较小的范围内,说明控制效果良好。图7为系统控制输入,位置和姿态输入信号均平滑稳定且抖振较小。

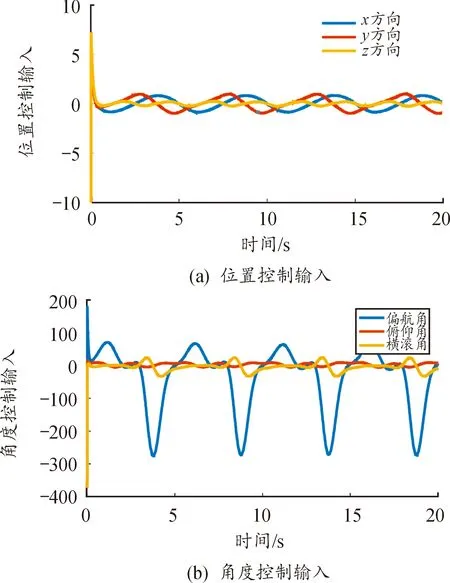
图7 系统输入控制信号Fig.7 System output control signal

通过对上述仿真结果的分析可知,本文所设计控制算法可以有效实现机器鱼的空间运动控制,同时也验证了该算法具有较快的收敛速度以及较好的稳定性,机器鱼空间运动轨迹平滑无较大波动,也证实了采用饱和函数代替符号函数的方法可有效降低滑模控制所产生的抖振现象。

4 实验验证

4.1 实验平台和环境

1) 实验平台。本文使用自主研发设计的3自由度胸鳍和三关节尾鳍协同推进的仿生机器鱼,其形状近似于流线型椭球,长×宽×高为0.65 m×0.17 m×0.23 m,总质量约为9 kg;内部装有深度传感器和陀螺仪,可实时监测运动位姿,如图8所示。

图8 仿生机器鱼实验样机Fig.8 Experimental prototype of biomimetic robotic fish

2) 实验环境。本文仿生机器鱼的实验水池长、宽和高分别为4.0 m、2.0 m和1.2 m,主要模拟静水环境,用于图像采集的摄像头距水池上方约3 m,池内水深约1 m。水池实验环境如图9所示。

图9 仿生机器鱼水池环境Fig.9 Biomimetic robot fish pool environment

4.2 螺旋下潜实验

采用所研制的仿生机器鱼样机,分别在实验室水池进行静水和动水2种工况下的实验。

1) 水池静水实验。在螺旋运动实体实验时,控制机器鱼胸鳍按式(1)规律运动,通过读取深度传感器和陀螺仪模块的反馈数据,使得控制器实时输出控制机器鱼胸/尾鳍运动的参数。静水工况机器鱼螺旋下潜运动如图10所示。

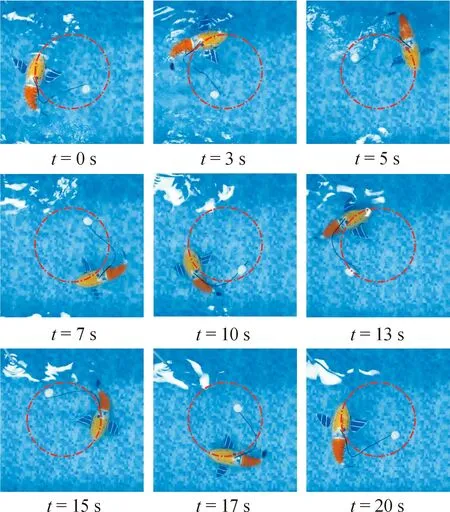
图10 静水工况机器鱼螺旋下潜运动Fig.10 Spiral diving motion of robotic fish under still water conditions

图11显示水池实验中机器鱼空间运动轨迹。通过对比发现机器鱼在螺旋下潜的初始阶段存在较大位置误差,约8 s后实际运动轨迹能更好的跟踪期望轨迹。当机器鱼运动至接近水池边缘和离开水池边缘区域时运动轨迹略有变形,导致该现象的主要原因是当机器鱼处于水池边缘时壁面效应加剧产生了较大的扰动。如图12所示,机器鱼在运动初始阶段有较大的位置误差,最大达0.1 m;8 s后位置误差显著降低,最大为0.06 m。机器鱼整体运动轨迹误差较小且无明显尖点,虽略有滞后但可保持平稳螺旋运动。

图11 机器鱼空间运动曲线Fig.11 Three-dimensional motion curve of robotic fish

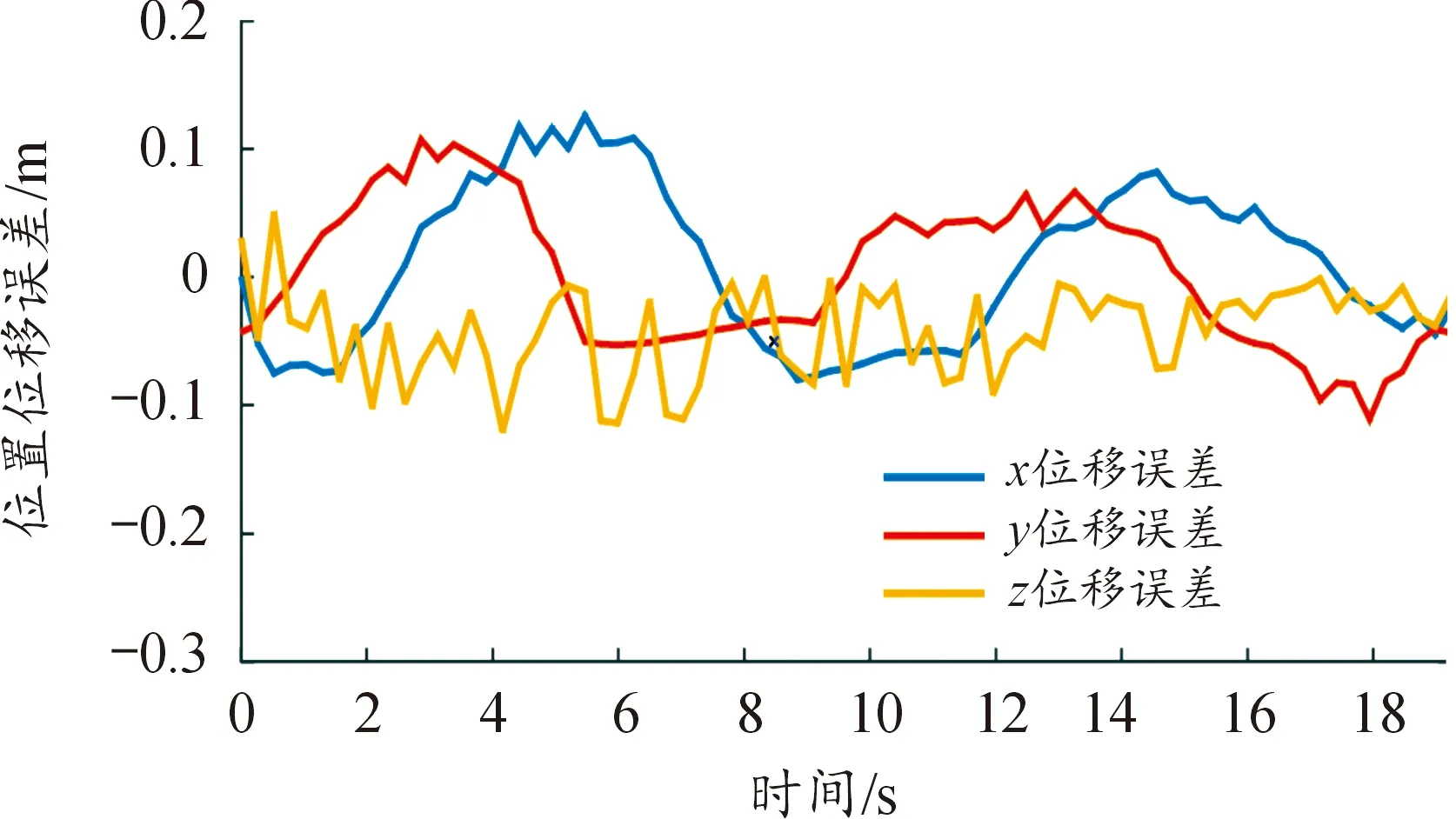
图12 机器鱼实际轨迹误差曲线Fig.12 Actual trajectory error curve of robotic fish

2) 水池动水实验。利用变频潜水泵搭建不同流速下的循环水池工况,其水流方向如图13黄色箭头方向,流速设定为0.1、0.3、0.5 m/s。对仿生机器鱼设定不同流速情况下与静水工况实验一致的运动规律,并采集其运动位姿数据。动水工况机器鱼螺旋下潜运动如图13所示。

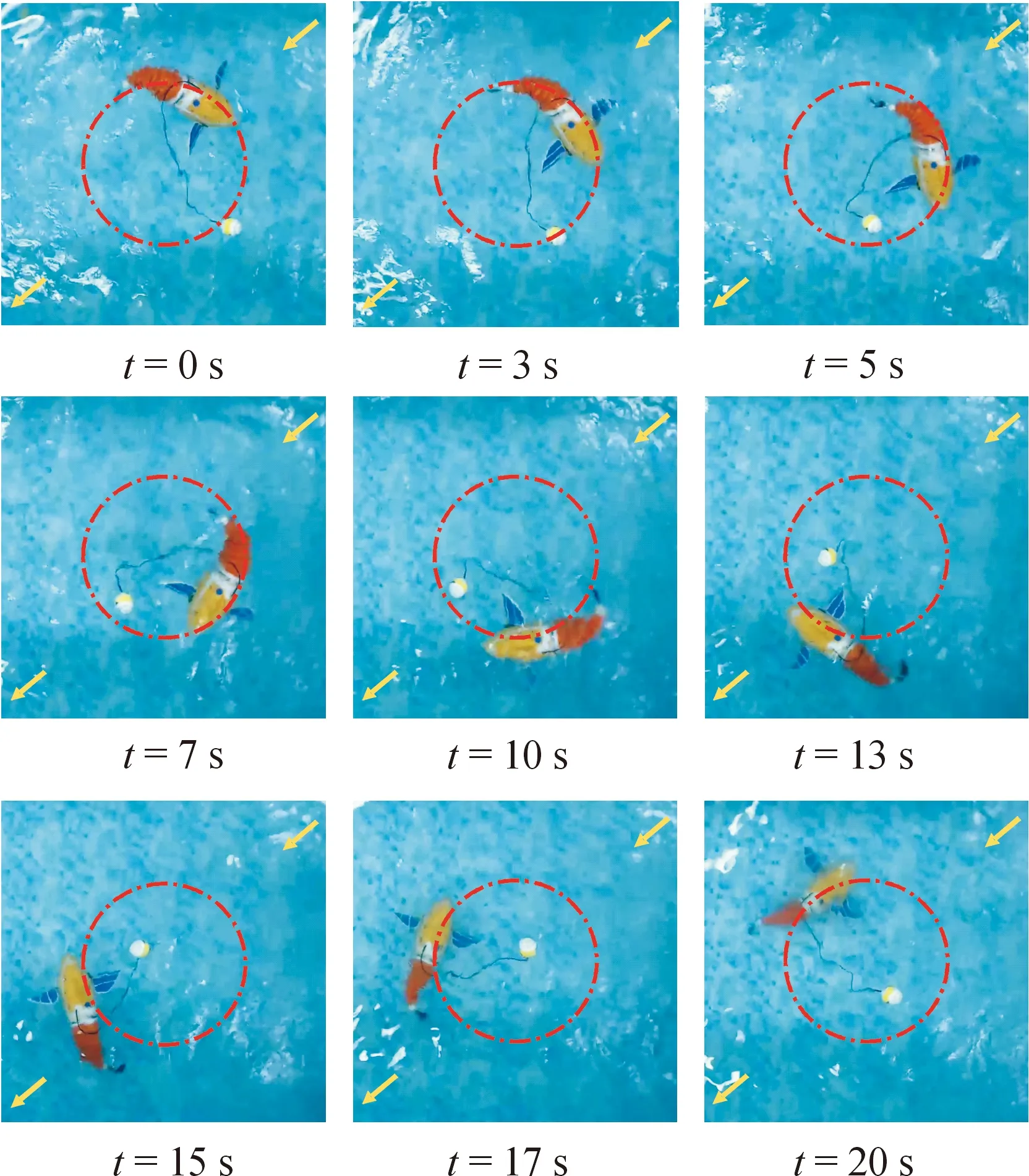
图13 动水工况机器鱼螺旋下潜运动Fig.13 Spiral diving motion of robotic fish under dynamic water conditions

如图14所示,在0.1 m/s流速下机器鱼运动位置误差和静水工况基本一致,而在0.3 m/s和0.5 m/s流速下,机器鱼运动朝水流方向有明显的滑移,流速越大滑移越大,最大达0.08 m,8 s后由于其潜入水中,滑移显著降低。但机器鱼运动误差较静水工况无明显变化,在3～7 s和13～17 s阶段,由于水池的壁面效应,其轨迹在靠近壁面处略有变形,误差较大,且流速越大壁面效应影响越大,将会出现流速与滑移不对应的情况,具体见图14中局部放大图所示。

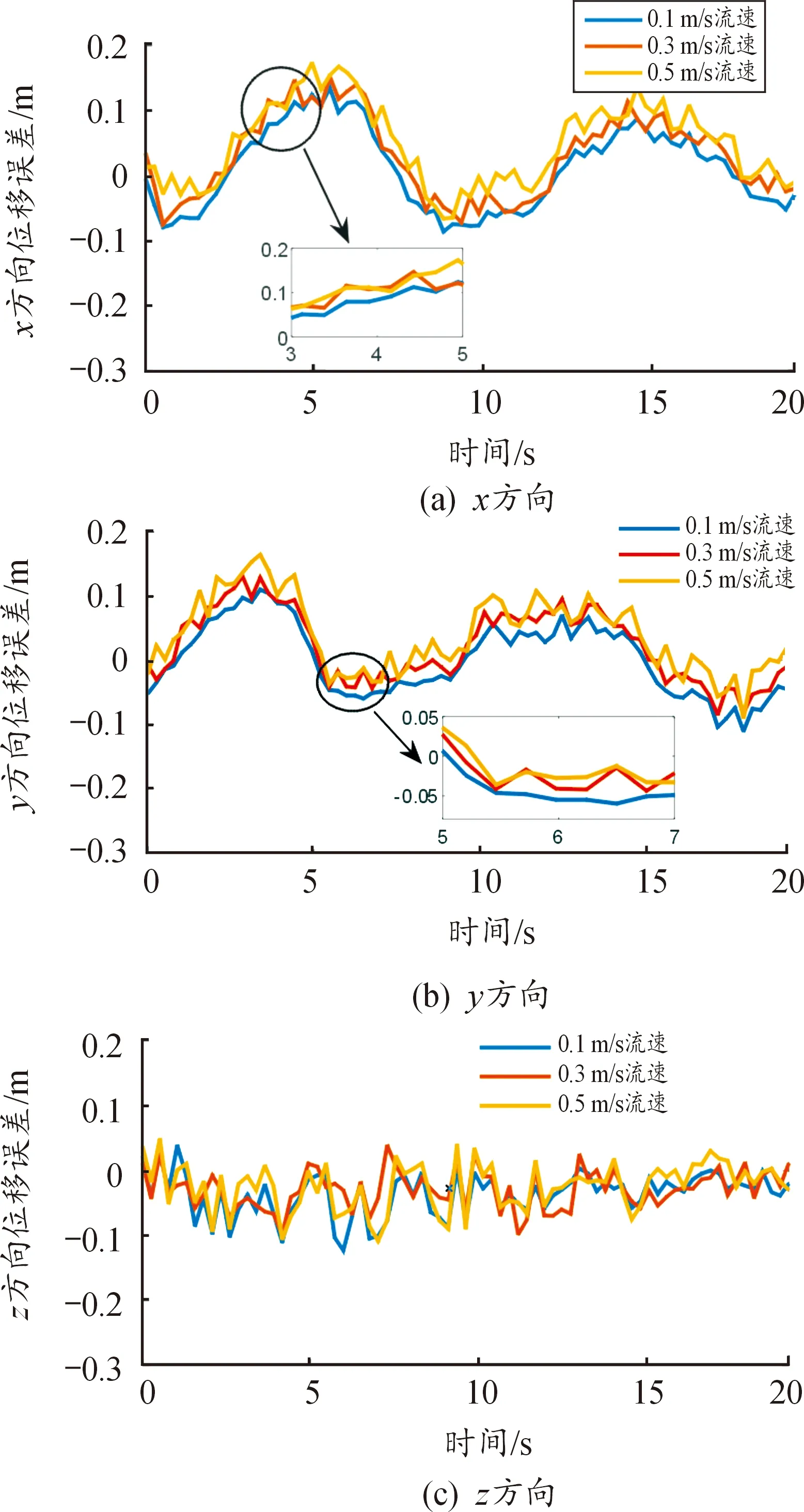
图14 不同流速下机器鱼实际轨迹误差曲线Fig.14 Actual trajectory error curve of robotic fish with different flow rates

通过水池动静水实体实验表明,水流对机器鱼螺旋运动时滑移影响较大,但运动轨迹依旧保持螺旋运动,并与期望基本保持一致,进一步验证了本文所设计控制方法的有效性,同时说明了所构建的仿真模型具有可参考性。

5 结论

本文针对3自由度胸鳍仿生机器鱼空间轨迹跟踪控制问题,在所建立胸鳍运动轨迹方程和水动力学模型基础上,提出了一种基于RBF神经网络自适应滑模控制方法。

1) 设计制作了具有3自由度胸鳍以及三关节尾鳍的仿生机器鱼样机,通过分析机器鱼运动机理设定胸鳍运动轨迹曲线并构建了机器鱼水动力学模型。

2) 通过RBF神经网络实现对机器鱼模型的实时逼近和补偿,并使用滑模控制方法实现运动轨迹的快速收敛,利用李雅普诺夫稳定性定理证明了该方法具有渐近稳定性。

3) 使用仿生机器鱼样机进行了室内水池实验,实验结果表明机器鱼在不同流速工况螺旋下潜运动时运动过程平稳,可实时跟踪空间运动轨迹。由于室内水池的壁面效应,其轨迹在靠近壁面处略有变形,最大轨迹误差为0.18 m;验证了本文所述方法的有效性。