基于物质点法Ti/Al3Ti层状复合材料抗斜侵彻性能研究

谢桂兰,侯 昆,龚曙光,宋慕清,肖芳昱,左立来

(湘潭大学 机械工程与力学学院, 湖南 湘潭 411105)

0 引言

Ti/Al3Ti层状复合材料具有高强度、高模量、高刚度、低密度以及高的断裂韧性等优异性能,在航空航天、武器装备及地面军用车辆的装甲防护系统等方面有着广阔的应用前景[1]。近年来,国内外学者从试验和数值模拟两方面对其抗侵彻性能进行了研究。Adharapurapu等[2]通过三点弯曲与拉伸试验研究了材料在垂直于叠层方向的断裂行为。Tiezheng Li[3]对不同钛合金体积分数的Ti/Al3Ti复合材料的各项力学性能进行了测试。Vecchio[4]用质量为10 g的钨合金平头弹对厚度为20 mm、Ti体积分数为20%的Ti/Al3Ti层状复合材料靶板进行了弹道冲击试验。Harach[5]开展了弹体以不同速度侵彻Ti/Al3Ti层状复合材料的弹道冲击试验。Zelepugin等[6]使用爆炸焊接加烧结的方法制备了11层、13层和23层的Ti/Al3Ti层状复合材料,并对弹体侵彻Ti/Al3Ti复合材料靶板和单相Ti合金、单相Al3Ti材料的过程进行了数值模拟。曹阳[7]在弹体速度为811.2 m/s的情况下,对体积分数为20%的Ti/Al3Ti层状复合材料靶板进行了弹道冲击试验。Price等[8]制备了具有剩余铝层的Ti/Al3Ti复合材料,并对其显微结构和组织性能进行了一系列观察与测试。印度国防冶金实验室[9]也通过弹道冲击试验对Ti/Al3Ti复合材料的防护性能进行了研究。史明东等[10]使用LS-DYNA非线性有限元软件对Ti/Al3Ti层状复合材料靶板的弹道侵彻过程进行了数值模拟。

目前国内外学者对于弹体侵彻Ti/Al3Ti层状复合材料的数值模拟过程多采用有限元法,但使用有限元法计算高速冲击等大变形问题时,容易产生网格畸变,影响计算精度与计算效率。物质点法是一种无网格法,采用拉格朗日和欧拉双重描述,将物体离散为一组在空间网格中运动的质点,质点携带了所有的物理信息。质点在空间网格中运动,运动方程在空间网格上求解,避免了网格畸变问题,适合于分析特大变形及流动问题,是分析超高速碰撞、冲击侵彻、爆炸、裂纹动态扩展等问题的有效方法[11]。

虽然国内外学者已对Ti/Al3Ti层状复合材料的防护性能进行了广泛的研究,但多集中于弹体垂直侵彻Ti/Al3Ti层状复合材料,缺少侵彻角度对Ti/Al3Ti层状复合材料防护性能影响的研究。而在实际情况中,弹体侵彻靶板时往往带有一定的角度,所以研究弹体斜侵彻Ti/Al3Ti层状复合材料的过程是很有必要的。

因此,采用物质点法对弹体斜侵彻Ti/Al3Ti层状复合材料的过程进行数值模拟,研究侵彻角度对弹体剩余速度、跳弹现象和Ti/Al3Ti层状复合材料能量吸收率的影响。

1 理论基础

1.1 物质点法基本理论

文献[11-12]中给出了物质点法的基本理论。物质点法将连续体离散为一组在空间网格中的质点,连续体的密度近似为:

(1)

式中:np为质点总数;mp是质点p的质量;δ是Dirac Delta函数;xip是质点p的坐标。在求解动量方程时,质点和背景网格完全固连,随背景网格一起运动,因此可以通过建立在背景网格结点上的有限元形函数NI(xi)来实现质点和背景网格结点之间信息的映射。质点p的坐标xip可通过结点坐标xiI插值得到,网格结点坐标与物质点之间的映射关系为:

xip=NIpxiI

(2)

式中,NIp=NI(xp),为结点I的形函数在质点p处的值。如果背景网格采用八节点六面体单元,则结点I的形函数为:

(3)

其中,ξI,ηI和ζI为结点I的坐标。质点P的位移uip及其导数uip, j可以由结点位移uiI插值得到,即:

uip=NIpuiI

(4)

uip, j=NIp, juiI

(5)

质点p的虚位移δuip也可近似为:

δuip=NIpδuiI

(6)

由此可以得到背景网格结点的运动方程:

(7)

其中第I个网格节点在i方向的动量为:

(8)

背景网格的质量矩阵为:

(9)

结点内力为:

(10)

结点外力为:

(11)

采用集中质量阵,可得:

(12)

动量piI可简化为:

(13)

此时背景网格结点的运动方程程式(7)可简化为:

(14)

由以上公式看出,物质点法与有限元法非常相似,但区别在于物质点法的背景网格只在每个时间步内与物体固连,在每个时间步结束时,丢弃已经变形的背景网格,由于质点已经携带了物体的所有信息,在下一个时刻,可以通过将质点的信息映射到新背景网格上来求得网格的信息。这样一来,就成功避免了网格畸变。

1.2 材料模型及参数

在计算过程中,弹体采用各向同性线性强化弹塑性材料模型,具体参数如表1[7]所示,其中,E为材料的弹性模量;ν为材料的泊松比;σy为材料的屈服应力;Et为材料的切线模量。

表1 弹体钢材料参数Table 1 Material parameters of steel for projectile

对于Ti/Al3Ti层状复合材料,采用Johnson-Cook模型描述Ti的力学行为,具体参数如表2[7]所示,其中,A为静态屈服极限;B为应变硬化系数;C为应变率系数;m为热软化指数;n为应变硬化指数;Tm为熔点;TR为室温。

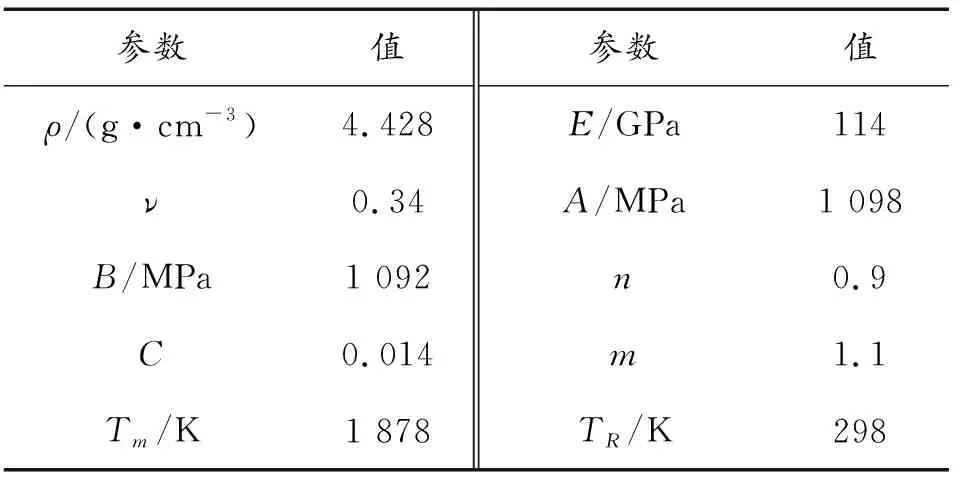
表2 Johnson-Cook本构模型材料参数Table 2 The material parameters of Johnson-Cook constitutive equation

在描述材料在高应变率下压力与体积变化的关系时,Johnson-Cook模型需要与Mie-Gruneisen状态方程配合使用[7],表3为Ti的Mie-Gruneisen状态方程参数。其中,γ0为压力为0时的Gruneisen常数,c0为材料的体积声速,S1为流体状态方程系数,用来描述材料冲击波速度与粒子速度之间的关系,E0为材料初始内能。

表3 Mie-Gruneisen状态方程参数Table 3 The parameters of Mie-Gruneisen state equation

Al3Ti金属间化合物为脆性材料,采用JH-2本构模型[13],具体参数如表4[7]所示。其中,A1、B1、C1、M1、N1为材料常数;T为材料能承受的最大静水拉应力;σHEL为Hugoniot弹性极限时的等效应力;PHEL为Hugoniot弹性极限时的静水压应力;β为能量转化系数;D1、D2为材料损伤度系数;K1、K2、K3为材料常数,其中K1为材料的体积模量。

表4 Al3Ti金属间化合物的JH-2模型参数Table 4 The parameters of JH-2 model for Al3 Ti intermetallic

2 物质点法的验证

根据物质点法理论,采用FORTRAN语言编写了模拟卵形弹侵彻Ti/Al3Ti层状复合材料的物质点法程序。为了验证物质点法模拟卵形弹侵彻Ti/Al3Ti层状复合材料的可行性,采用文献[7]中的几何参数进行建模和模拟计算,并将计算得到的结果分别与文献[6]中的试验及文献[7]中的有限元模拟结果进行对比。图1为卵形弹侵彻Ti/Al3Ti层状复合材料的几何模型示意图,弹体材料为钢,直径为6.2 mm,弹体总长度为27.6 mm,弹头长为12.6 mm,弹体速度为802.6 m/s。Ti/Al3Ti层状复合材料靶板尺寸为80 mm×80 mm×7 mm,总层数为17层,其中Ti为9层,每层厚度为0.17 mm,Al3Ti金属间化合物为8层,每层厚度为0.68 mm。

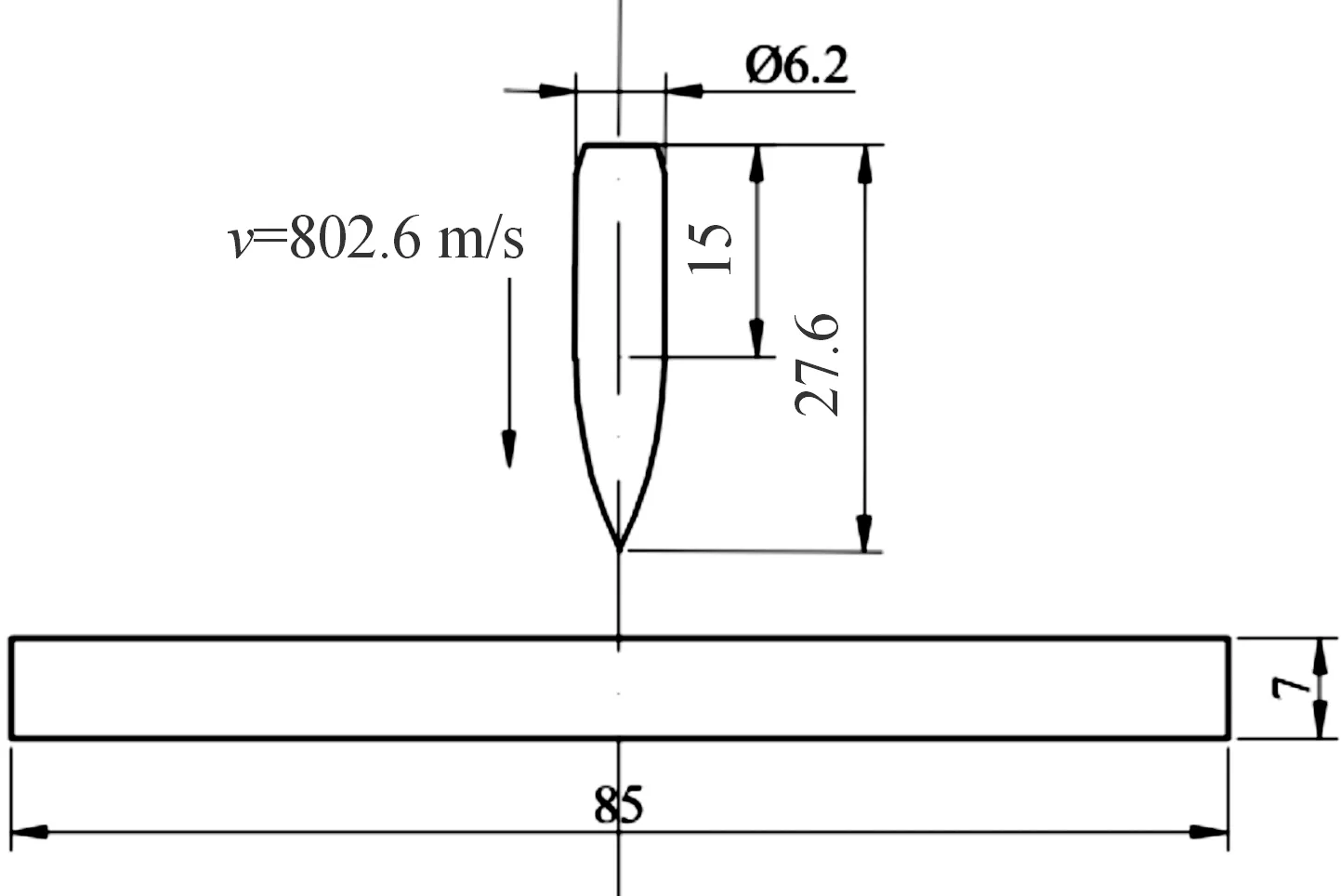
图1 卵形弹侵彻Ti/Al3Ti层状复合材料的几何模型示意图Fig.1 Schematic diagram of the geometric model of the oval projectile penetrating the Ti/Al3Ti laminate composites

图2为卵形弹侵彻Ti/Al3Ti层状复合材料的物质点法离散模型。由于结构对称,采用1/4计算模型以提升计算效率,并在对称面上施加对称边界条件。弹体与靶板的质点间距均为0.17 mm,背景网格尺寸为0.4 mm×0.4 mm×0.4 mm,质点总数为2 298 543个。时间步长因子设为0.9,模拟时间为60 μs。材料参数如表1—表4所示。

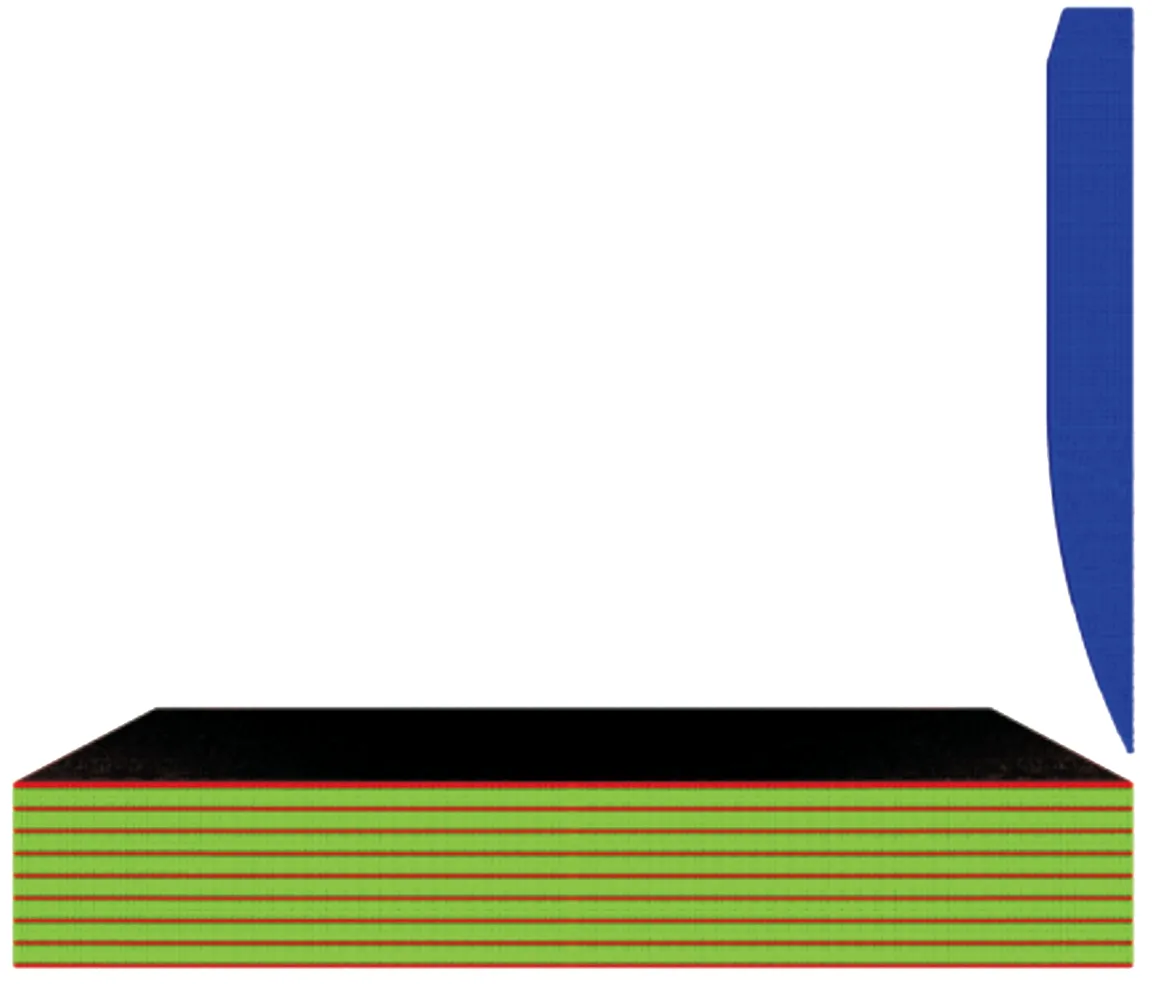
图2 卵形弹侵彻Ti/Al3Ti层状复合材料物质点离散模型Fig.2 Discrete model of material point for oval projectile penetrating Ti/Al3Ti laminate composites

图3为弹道冲击物质点法模拟和试验结果[6]对比。试验结果中,弹体剩余速度为711.8 m/s,而物质点法模拟得到的弹体剩余速度为709.6 m/s,误差仅为0.3%。图4为物质点法与有限元法[7]模拟得到的弹体剩余速度时程曲线结果。

图3 弹道冲击物质点法模拟和试验结果对比Fig.3 Comparison of ballistic impact results obtained between test and material point methods

由图3可以看出,靶板迎弹面均出现扩孔破坏,靶板背弹面均产生花瓣状破坏,说明物质点法能有效模拟Ti/Al3Ti层状复合材料的损伤形式。由图4可以看出,物质点法模拟得到的弹体速度时程曲线和有限元法模拟得到的弹体速度时程曲线基本一致。说明物质点法模拟弹体侵彻Ti/Al3Ti层状复合材料的过程是可行有效的。

3 弹体斜侵彻Ti/Al3Ti层状复合材料的数值模拟

3.1 计算模型

为分析弹体入射角度对Ti/Al3Ti层状复合材料防护性能的影响,将弹体轴线与Ti/Al3Ti层状复合材料法线的夹角定义为θ,θ的取值为0°、15°、30°、45°。图5为弹体斜侵彻Ti/Al3Ti层状复合材料的几何模型示意图,弹体及Ti/Al3Ti层状复合材料的几何尺寸均与第2节相同,弹体入射速度分别为500、600、700、800 m/s。

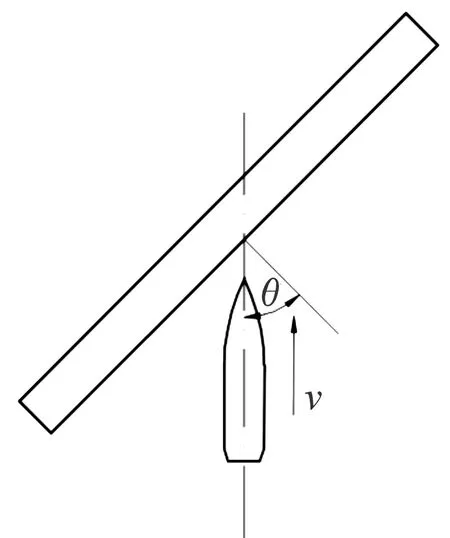
图5 弹体斜侵彻Ti/Al3Ti层状复合材料几何示意图Fig.5 Geometrical schematic diagram of projectile oblique penetration in to Ti/Al3Ti laminate composites

图6为弹体斜侵彻Ti/Al3Ti层状复合材料的物质点法离散模型,其余设置与第2节相同。

图6 弹体斜侵彻Ti/Al3Ti层状复合材料物质点离散模型Fig.6 Discrete model of material point for projectile oblique penetrating into Ti/Al3Ti laminate composites

3.2 模拟结果

图7为不同入射角度下,弹体斜侵彻Ti/Al3Ti层状复合材料的模拟结果图。

由图7可以看出,随着入射速度和入射角度的增大,Ti/Al3Ti层状复合材料损伤越大,且当入射角度θ=45°时,发生了明显的跳弹现象此外,弹体也发生了明显的弹道偏转。表明随着入射角度的增大,Ti/Al3Ti层状复合材料抗侵彻能力增加。

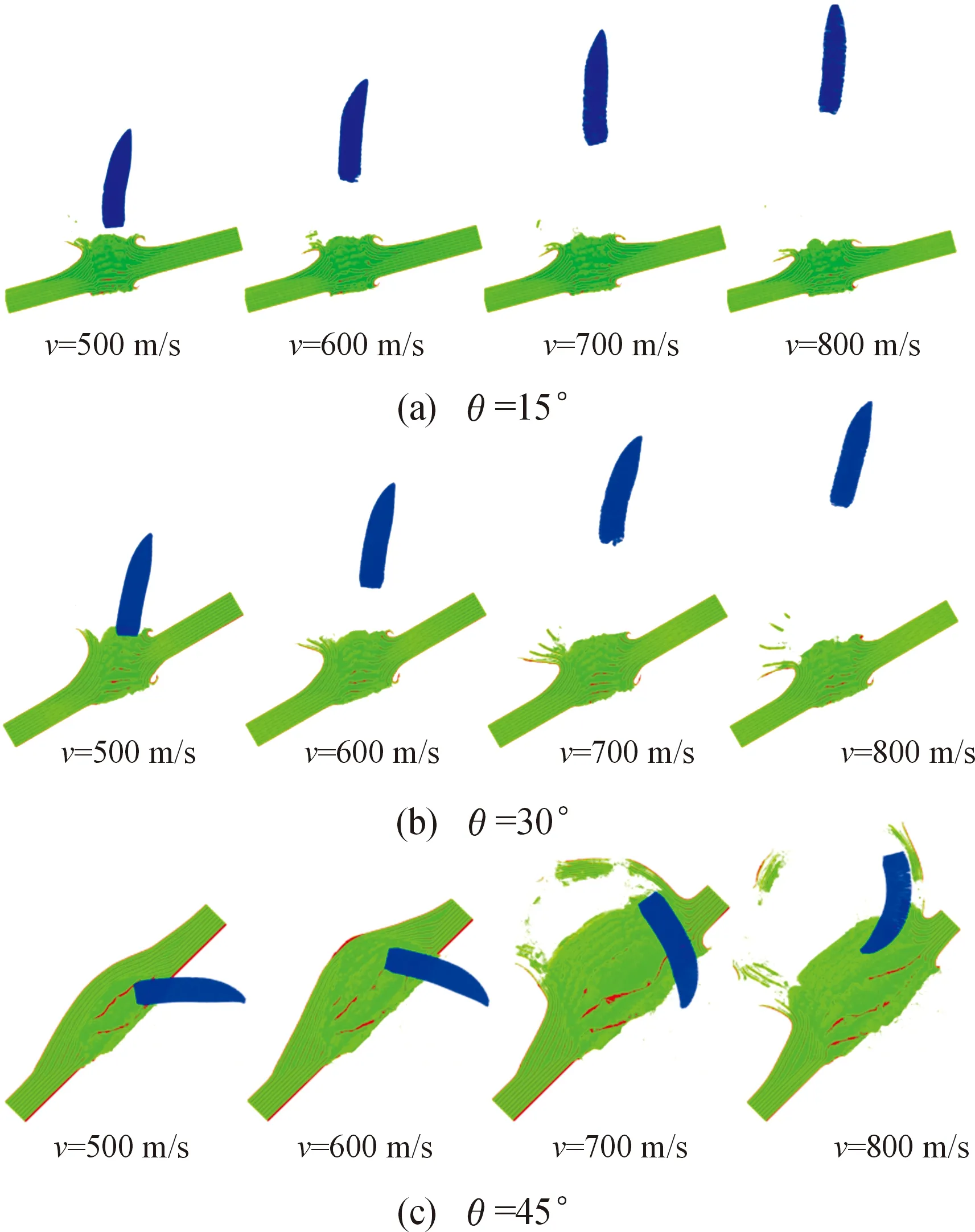
图7 弹体斜侵彻Ti/Al3Ti层状复合材料的模拟结果图Fig.7 Simulation results of projectile obliquely penetrating into Ti/Al3Ti laminate composites

3.3 弹体剩余速度分析

表5和表6为不同速度下,弹体侵彻Ti/Al3Ti层状复合材料得到的z轴和x轴方向上的剩余速度(vz和vx)。图7为弹体入射角度与弹体z轴和x轴方向上剩余速度的关系图。图8弹体入射角度与弹体剩余速度的关系图。

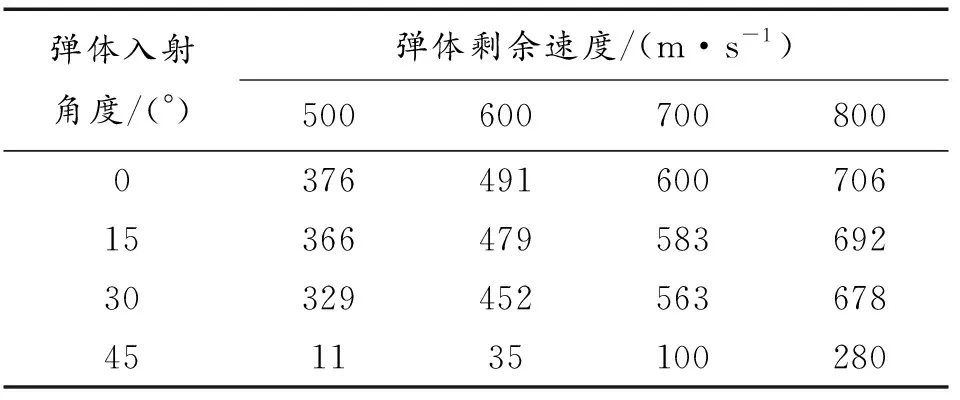
表5 弹体在z轴方向上的剩余速度Table 5 The remaining velocity of the projectile in the z-axis direction

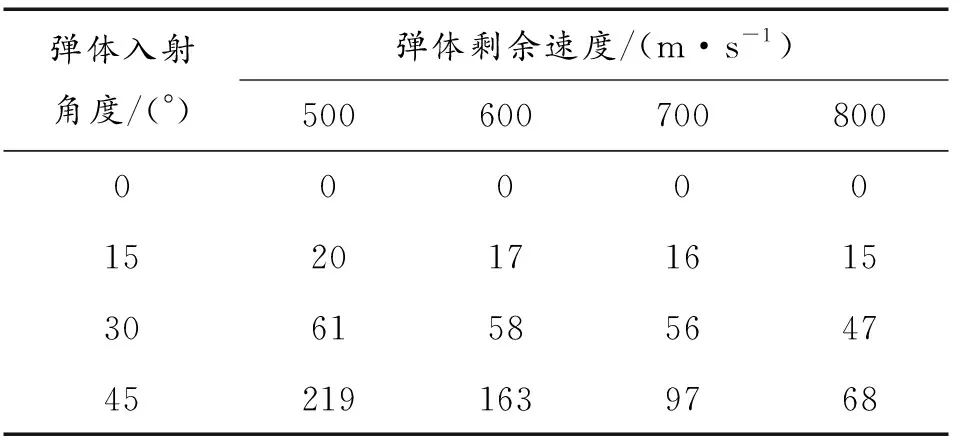
表6 弹体在x轴方向上的剩余速度Table 6 The remaining velocity of the projectile in the x-axis direction

从表5、表6和图8可以看出,弹体斜侵彻Ti/Al3Ti层状复合材料得到的剩余速度vz总是低于正侵彻得到的剩余速度,且弹体入射角度越大,vz越低、vx越高。这是由于弹体入射角度越大,Ti/Al3Ti层状复合材料在z轴方向上的等效厚度就越高[14],这意味着弹体侵彻的距离随着弹体入射角度的增加而增加,故vz不断下降。此外,随着弹体入射速度的增加,vz呈现出上升的趋势,vx呈现降低的趋势。这是由于弹体入射速度越大,弹体与Ti/Al3Ti层状复合材料的接触时间就越短,弹体消耗的动能也就越小,压力作用在弹体在x轴方向上的时间也越短,故vz上升、vx降低。

图8 弹体入射角度与弹体剩余速度的关系图Fig.8 The relationship between the incident angle of the projectile and the residual velocity

3.4 能量吸收率分析

能量吸收率α为弹体损失的动能ΔEk与弹体初始动能Ek的比值[15],即:

(15)

弹体入射速度与Ti/Al3Ti层状复合材料能量吸收率的关系图如图9所示。

根据图9可以看出,随着弹体入射角度θ的增加,Ti/Al3Ti层状复合材料的能量吸收率α也增加,表明随着入射角度的增大,Ti/Al3Ti层状复合材料抗侵彻能力增加。

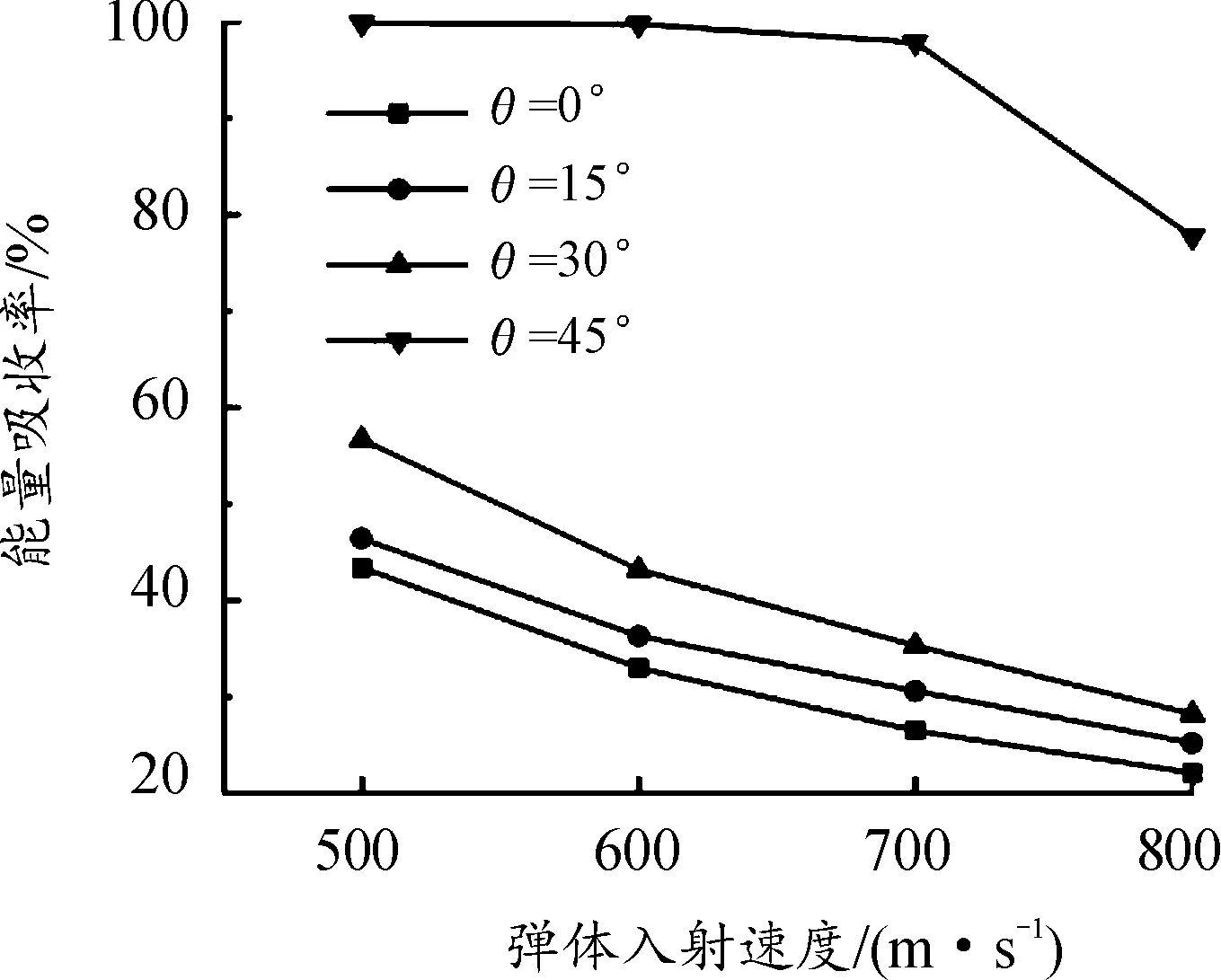
图9 弹体入射速度与Ti/Al3Ti层状复合材料能量吸收率的关系图Fig.9 The relationship between projectile incident velocity and energy absorption rate of Ti/Al3Ti laminate composites

4 结论

采用物质点法,建立了弹体侵彻Ti/Al3Ti层状复合材料的数值仿真模型,开展了弹体斜侵彻Ti/Al3Ti层状复合材料的仿真分析,研究了侵彻角度对Ti/Al3Ti层状复合材料弹体剩余速度和能量吸收率的影响,得到以下结论:

1) 物质点法模拟弹体侵彻Ti/Al3Ti层状复合材料得到靶板迎弹面出现扩孔破坏及靶板背弹面产生花瓣状破坏与已有文献试验结果吻合较好;且剩余速度与文献中结果误差仅为0.3%,计算精度较高;物质点法模拟得到的弹体剩余速度时程曲线与已有文献有限元法计算曲线基本一致。表明物质点法模拟弹体侵彻Ti/Al3Ti层状复合材料的过程是可行有效的。

2) 弹体入射角度θ从0°增加到45°时,弹体剩余速度减少,Ti/Al3Ti层状复合材料的能量吸收率从43.4%增加至99.9%,且当入射角度θ=45°时,发生了明显的跳弹现象。表明随着入射角度的增大,Ti/Al3Ti层状复合材料抗侵彻能力增加。