基于SDT模型和蒙特卡洛法的枪械抛壳机构公差分析

位跃东,方 峻

(南京理工大学, 南京 210094)

0 引言

在枪械产品生产制造过程中,由于枪械产品零件尺寸小、形状不规则、精度要求较高,且在计算装配尺寸链涉及尺寸较多,计算尤为复杂。因此为了提高枪械产品质量,保证装配精度,对枪械典型机构进行公差分析显得尤为重要。目前,在三维公差设计领域,采用小位移旋量(small displacement torsor,SDT)模型和蒙特卡洛法可以较为精确地描述公差及其误差累加分析。

小位移旋量理论最早是在1996年由Bourdet[1]应用到公差领域,并提出了基于SDT的几何要素公差数学表示方法。Desrochers和Chie[2]将机器人运动学中的Jacobian模型和SDT模型相结合提出了一种Jacobian-Torsor模型。Li[3]采用SDT和误差传播理论进行了公差分析。胡洁[4]研究了三维公差累积运动学模型,并给出了三维公差累积的运动学模型的一般形式。吴兆强[5]研究了SDT的公差建模方法,并结合齐次坐标逐步法进行了三维公差分析。吕程[6]基于SDT的公差建模,研究了蒙特卡洛法与响应面方法相结合的公差模型求解方法。

一般来说,公差分析方法主要有极值法[7](完全互换法)、概率法(不完全互换法)[8]和蒙特卡洛法[9]三种方法。极值法和概率法用于计算复杂装配尺寸链时计算效率低、工作量大,相比之下蒙特卡洛法在解决三维公差分析等复杂问题时应用更广,且符合实际生产情况。蒙特卡洛法又被称为统计模拟法,是一种基于概率统计理论,使用随机数来解决很多计算问题的方法[10]。通过蒙特卡洛法可以进行由各种随机变量组成的线性、非线性尺寸链计算,极大的提高了计算效率。

本文重点在基于前人的基础上,将SDT公差参数化建模与蒙特卡洛法相结合提出了一种新的公差分析方法,并进行实例分析验证。以枪械抛壳机构为例,采用SDT进行几何特征表面公差参数化建模,并结合齐次坐标变换矩阵进行装配路径上的误差累积分析,最后采用蒙特卡洛法在参数变动区间内进行随机抽样并进行计算,得到装配精度分析模型。

1 理论分析

1.1 基于小位移旋量法的公差数学模型表达

小位移旋量法是公差分析的基础,广泛用于表示几何特征面的理想形状偏差量。在公差分析当中,装配中单个部件的公差很可能会静态积累,并以运动方式传播,导致总体装配部件的关键尺寸发生变化。为了更好的对几何特面公差域进行参数化建模,采用SDT模型可以将公差表面上几何要素的变动转化为在公差域内随机变动点的集合。由于SDT模型是由旋转矢量和平动矢量组成,其部分参数取值范围的不同,可以表现为不同的公差类型。

SDT模型由旋转矢量R=[Δα,Δβ,Δγ]和3个平移矢量P=[Δu,Δv,Δw]描组成,SDT矩阵形式如下:

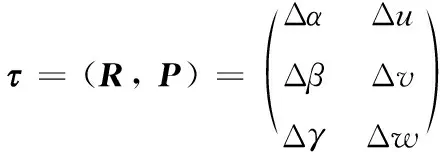
(1)

式中:Δα,Δβ,Δγ为单位旋转矢量在局部坐标系x,y,z轴上的投影;Δu,Δv,Δw为单位平移矢量在局部坐标系轴x,y,z上的投影。

SDT矩阵向量各分量的变化,可以认为是在笛卡尔坐标系下几何要素和几何特征在空间上的位移变化。因此根据机器人运动学坐标变换理论[11],可以将小位移旋量转换成齐次坐标矩阵来表示理想几何要素中点集的空间运动,齐次坐标矩阵T为:

(2)

表1列举了典型几何公差的小位移旋量和齐次变换矩阵。

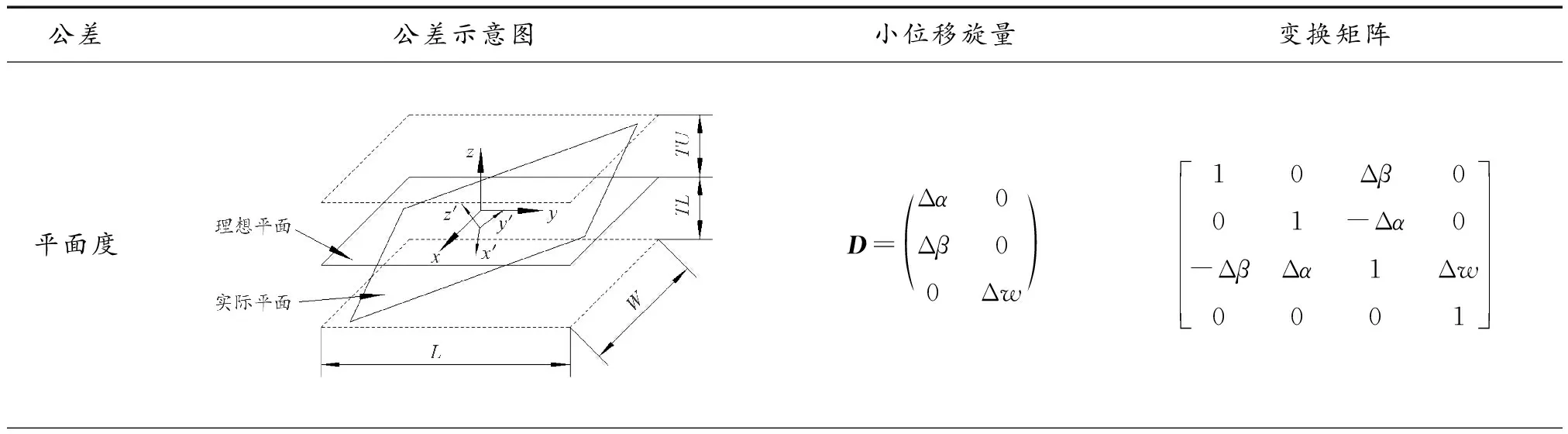
表1 典型几何公差及其对应的小位移旋量和变换矩阵Table 1 Typical geometric tolerance and its corresponding small displacement screw and transformation matrix

续表(表1)

1.1.1尺寸公差参数化建模

尺寸公差的变动不影响几何特征的形状、位置和角度变动等,常见的尺寸公差域如下所示。图1中左图为线性长度尺寸公差的旋量模型可表示[0,0,0;Δu,0,0]T,右图为直径尺寸公差了通过小位移旋量模型表示为[0,0,0;Δu,Δv,0]T。

1.1.2几何公差参数化建模

几何公差中主要分为形状公差、定向公差、位置公差和跳动公差4类[12]。其中形状公差和位置公差应用最为广泛。由于零件加工时不可避免地存在着误差,其中零件表面、轴线与中心对称平面等在加工后与所要求的理想位置和形状之间存在着一定范围的误差,这种误差被称为形位公差。为了保证枪械零件的产品质量,需要在零件设计时需要对几何要素规定合理的形位公差。本文以平面度和圆柱度为例进行了SDT公差参数化建模,其他类型的公差可参考类推。

1) 平面度公差域模型表达

平面度公差带是距离为公差值的两平行面之间区域,一般用来表示约束理想特征平面的最大偏移量。平面度公差域示意图如图2所示。

图2 平面度公差域示意图Fig.2 Schematic diagram of flatness tolerance area

在实际平面和理想平面建立相应的局部坐标体系。利用机器人运动学坐标变换理论,实际平面x′,y′,z′相对于理想平面x,y,z的旋转矩阵R为:

(3)

实际平面相对于理想坐标系的平移矩阵为D=[0,0,Δw]T。根据三角函数无穷小等价公式sinα≈α,cosα=1。故齐次变换矩阵模型可近似等价为:

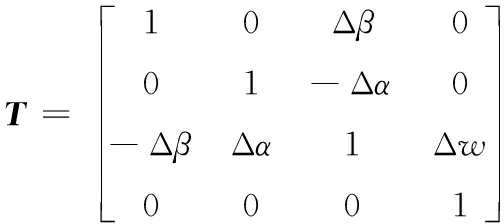
(4)

因此平面度公差域中几何特征上任何一点A的位置描述都可以通过齐次坐标变换矩阵表示为:

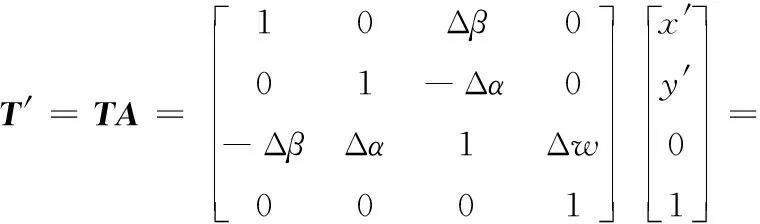
(5)

其中x′,y′分别为A点相对于实际平面坐标系x′,y′,z′下的坐标,平面内点的z′=0。平面度公差模型的约束条件为:

(6)

2) 圆柱度公差域模型表达

根据圆柱度公差定义,圆柱度公差域为两同心圆柱面之间的区域,用于表示实际圆柱面与理想平面的最大偏差范围。圆柱度公差域的示意图如图3所示。

圆柱实际平面相对于理想平面的位置可以分解为沿x和y轴的旋转矢量和移动矢量。利用机器人运动学坐标变换理论,实际平面的坐标体系相对于理想平面坐标系的SDT模型表达为。

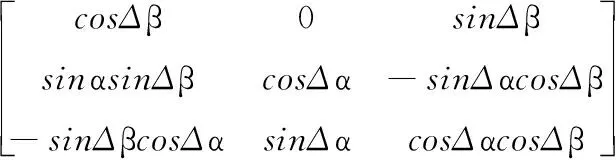
(7)

圆柱度公差域内实际几何特征上任意一点A的SDT模型T′表示为:

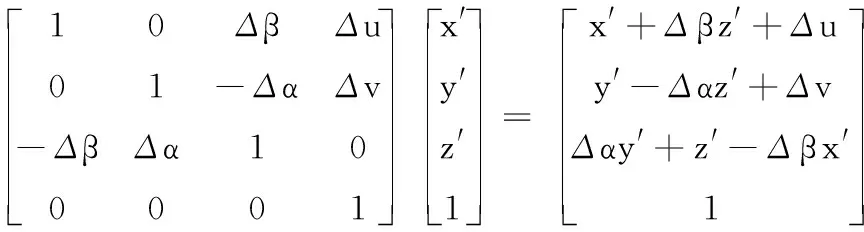
(8)

旋量参数的约束条件为:

(9)

1.2 基于蒙特卡洛的SDT法累积公差分析

蒙特卡洛法公差分析是通过求解随机变量的概率统计来计算封闭环的尺寸公差。根据已确定的几何变动类型约束,建立基于SDT模型的几何要素变动和约束方程,结合蒙特卡洛法筛选出符合公差边界条件与约束条件的随机数,采用齐次坐标变换矩阵对装配误差进行公差累加分析。重复试验次数直到样本总量,从而求出样本均值与方差,得出测量尺寸的分布直方图与贡献度分析。

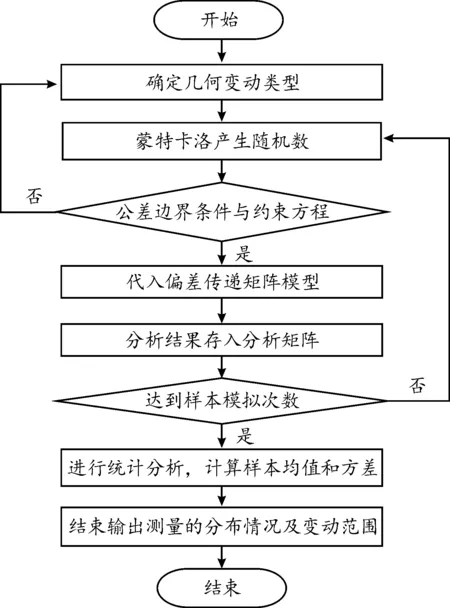
图4 基于SDT模型和蒙特卡洛法公差分析Fig.4 Tolerance analysis based on SDT model and Monte Carlo method

2 枪械抛壳机构公差分析实例

在弹头发射后,枪械中的拉壳钩将弹壳从弹膛中抽出后,在抛壳挺的作用下撞击后退的弹壳从而将其抛出,抛壳机构即将弹壳从弹膛内推出并抛出枪外的部件。为了保证弹壳被顺利抛出,保证枪械机构动作的可靠性,对装配部件的尺寸要求显得尤为重要。本文通过控制抛壳挺与弹壳之间叠盖量的范围,来保证抛壳机构的可靠性。

本文中通过控制抛壳挺与弹壳之间水平方向上的叠合量需要控制在一定范围内,来保证抛壳机构的可靠性。

抛壳机构主要由机匣体、弹壳、拉壳钩、抛壳挺等零件组成。图5为抛壳挺机构三维示意图。

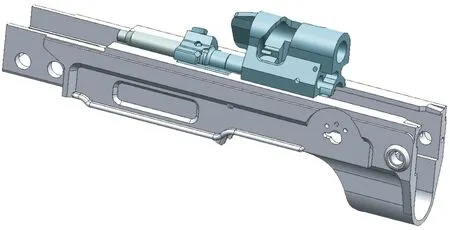
图5 抛壳机构三维装配示意图Fig.5 3D assembly diagram of shell throwing mechanism

将机构沿弹底平面进行剖视图分析,其中抛壳挺与弹底平面重叠的尺寸的水平距离为本次分析的目标尺寸,叠盖量会影响装配的质量,对枪械的可靠性有着重要的影响。图6为抛壳机构剖视图。抛壳机构的零件尺寸公差见表2。

图6 抛壳机构二维装配示意图Fig.6 2D assembly diagram of shell throwing mechanism

表2 抛壳机构的零件尺寸公差Table 2 Dimensional tolerance of parts of shell throwing mechanism

图7是根据装配约束关系建立的装配尺寸链分析图,箭头方向表示公差传递的方向。

图7 装配尺寸链分析图Fig.7 Assembly dimension chain analysis diagram

将所有组成环沿封闭环的水平方向投影:

(10)

将所有环沿竖直方向上投影:

(11)

式(10)、式(11)中封闭环X为抛壳挺与弹底平面水平方向上的叠盖量。

2.1 极值法求解

极值法从尺寸链各环的最大与最小极限尺寸进行计算,不考虑各环实际尺寸的分布情况[13]。通过极值法计算出来的尺寸进行加工各组成环,不需要挑选或人工修锉便可进行装配,且装配后即封闭环亦能满足装配精度要求,实现百分百零件完全互换。

平面尺寸链的封闭环公等同于各组成环传递系数与组成环公差乘积的和,根据各组成环公差值计算结果如下:

(12)

式中:Ti为封闭环公差(其中i=1,2…,n为封闭环的个数);εi为组成环传递系数;

2.2 概率法求解

概率法求解封闭环公差,根据尺寸链中各组成环均服从于正态分布概率模型的随机变量,且组成环之间相互独立,在此基础上进行公差分析。应用概率论原理的概率法求解尺寸链的方案更加符合实际的生产情况,并且组成环数目越多,采用概率统计法就越经济。概率法以保证绝大多数产品可以互换,各组成环无需挑选或改变尺寸大小和位置直接进行装配,就能达到封闭环的精度要求。

根据各组成环公差值通过概率法求解封闭环公差为:

(13)

式中:ξi为误差传递系数;Ti为各组成环(其中i=1,2…,n为封闭环的个数)。

2.3 蒙特卡洛模拟法求解

2.3.1蒙特卡洛法生成随机模拟点

蒙特卡洛公差分析[14]是基于SDT模型的几何公差参数化建模求解出的公差边界条件与约束方程,对公差域内的几何特征面上模拟产生随机点,且筛出掉不满足边界条件与约束方程的随机数,并使用SDT模型表示。当产生的随机点符合样本量时,将生成的模拟点代入到偏差传递矩阵及进行下一步的计算。设产生的随机数点为P,则P点的齐次坐标坐标变换公式为:

(14)

式中:Pi为相对于i坐标系下的相对坐标;T为小位移旋量齐次变化矩阵。

2.3.2装配误差累积

在计算封闭环的尺寸公差时,本文采用齐次坐标变换的方法来描述几何特征要素在装配体之间的累积传递。首先以弹底平面圆心为坐标原点建立固定坐标系,然后在每个装配表面建立局部坐标系,几何特征之间的误差通过装配表面之间的运动学关系进行误差传递,如图8所示。该机构共有9处误差传递。从固定坐标系出发,沿着装配约束经过每个装配特征平面,最终回到固定坐标系。

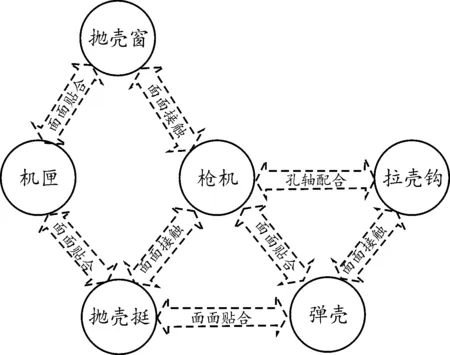
图8 抛壳机构装配几何关系图Fig.8 Geometric relation diagram of shell throwing mechanism assembly

在装配误差累积分析中,几何特征要素之间误差传递是基于齐次坐标变换方法描述的。齐次坐标变换矩阵是机器人运动学中用来描述2个平面相对位置的矩阵。如图9所示,平面2相对于平面1的位置通过齐次坐标描述为:

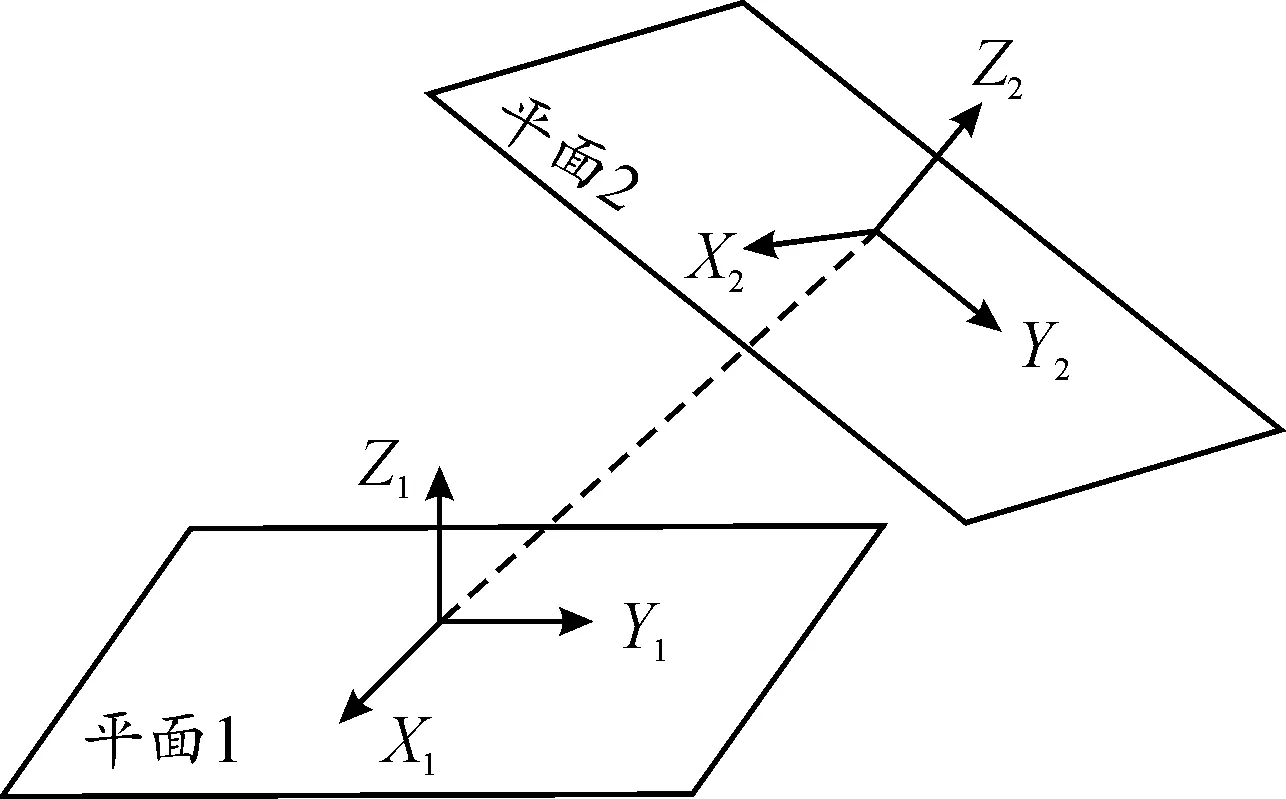
图9 两平面的相对方位示意图Fig.9 Schematic diagram of relative orientation of two planes

(15)

从固定坐标系出发,经过n个装配几何特征面的局部坐标系,最终回到固定坐标系,形成一个闭环回路,最终得到公差累积模型。装配误差传递如图10所示。

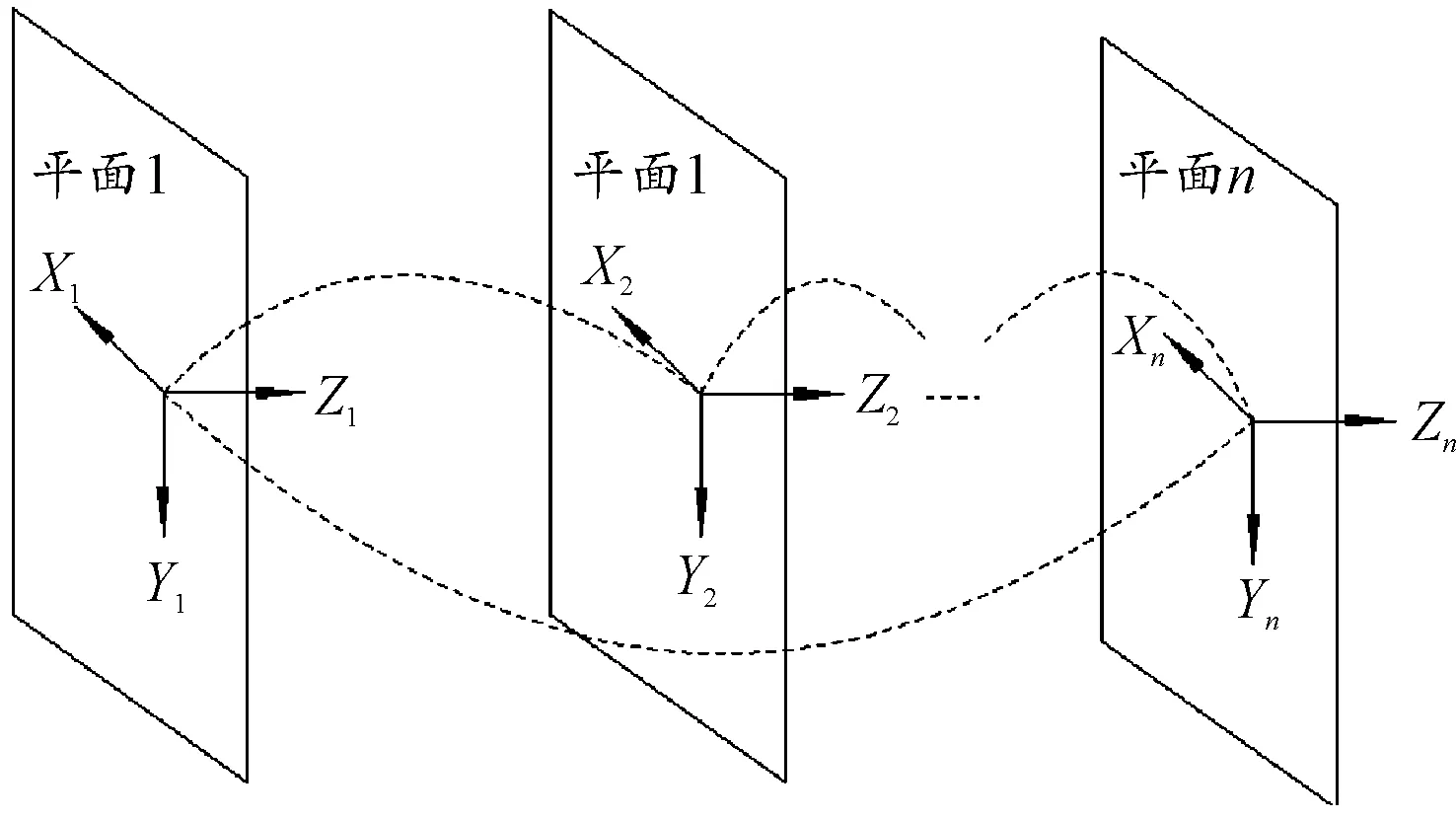
图10 装配体中装配误差传递示意图Fig.10 Schematic diagram of assembly error transmission in assembly

装配体中平面n相对于固定坐标系的误差传递齐次变换矩阵nT0可表示为:

nT0=1T0·2T1… ·nTn-1

(16)

2.3.3蒙特卡洛公差分析计算

通过SDT模型对装配体中各几何特征表面进行参数化表达后,结合蒙特卡洛法,将包含几何特征信息的特征面转化公差域内的随机点的SDT集合,并代入到误差传递坐标矩阵,从局部坐标系向固定坐标系(起始坐标系)转换,得到包含各参数的抛壳机构公差累积模型:

(17)

式中:iTi-1为平面i相对于平面i-1的齐次坐标旋量矩阵;Pi为含有旋量参数的名义尺寸误差齐次坐标矩阵;M为固定坐标系几何要素上任一点的坐标矩阵;X为封闭环的偏差矩阵;n为变动特征面的个数。

其中典型零部件的装配偏差传递矩阵和尺寸误差变动矩阵的主要数据如表3所示。

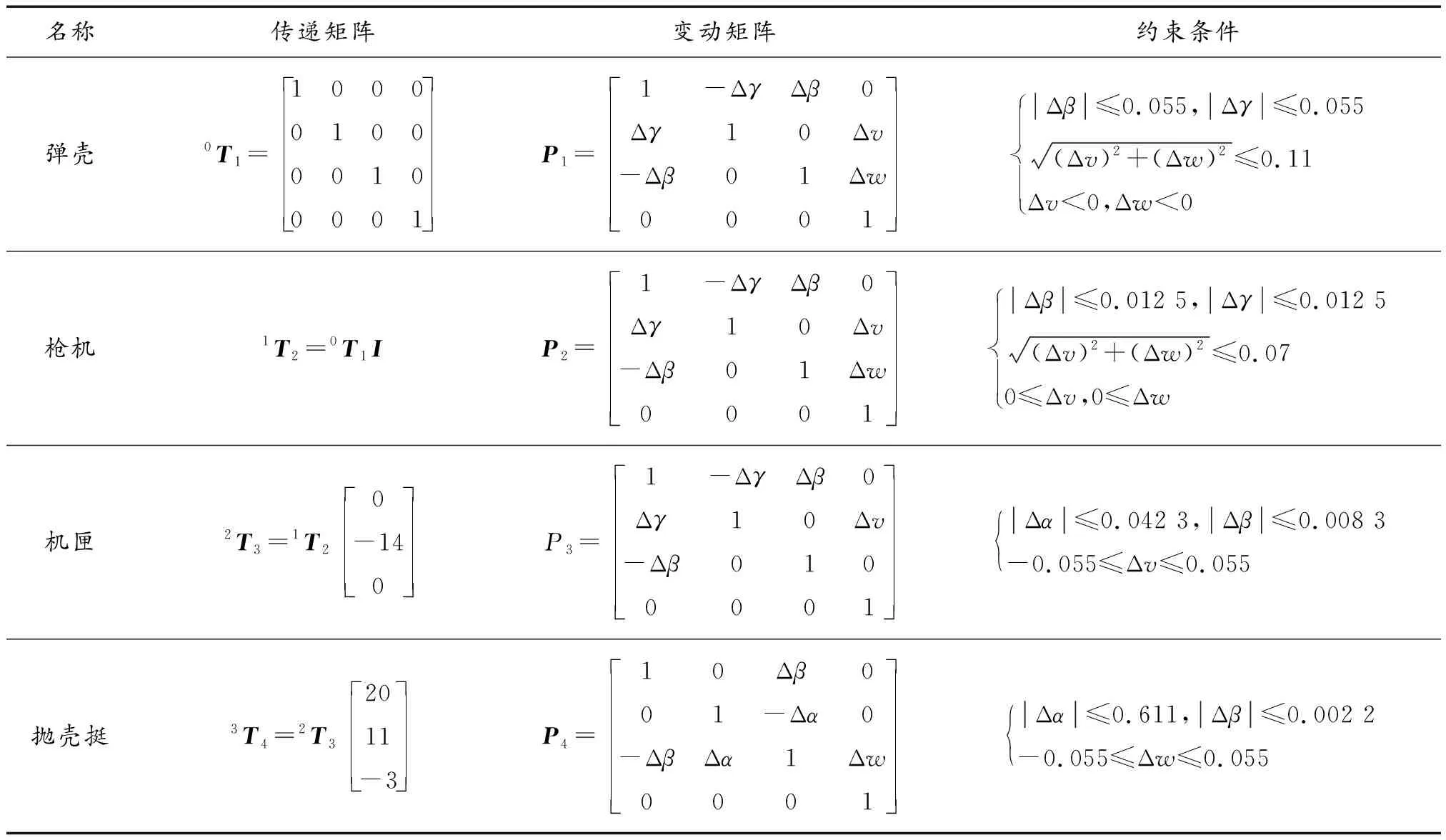
表3 装配偏差传递矩阵尺寸误差变动矩阵Table 3 Assembly deviation transfer matrix and dimensional error variation matrix

2.3.4蒙特卡洛仿真分析结果

蒙特卡洛法是基于6σ原则,即尺寸公差在μ±3σ这一范围概率高达99.37%,我们认为在公差在这一范围内的零件是合格的。并且组成环的数目越多,尽管尺寸公差服从于不同的分布规律,但是封闭环的误差分布都接近于正态分布规律,且蒙特卡洛法抽样次数越多,越接近于正态分布,结果越精确。本文通过采用2 000、5 000、10 000、20 000个样本点进行基于蒙特卡洛抽样法的装配模拟仿真。叠盖量尺寸分布直方图如图11—图14所示。

图11 模拟2 000次的叠盖量尺寸分布直方图Fig.11 Overlay size distribution histogram of 2 000 simulations

图12 模拟5 000次的叠盖量尺寸分布直方图Fig.12 Overlay size distribution histogram of 5 000 simulations

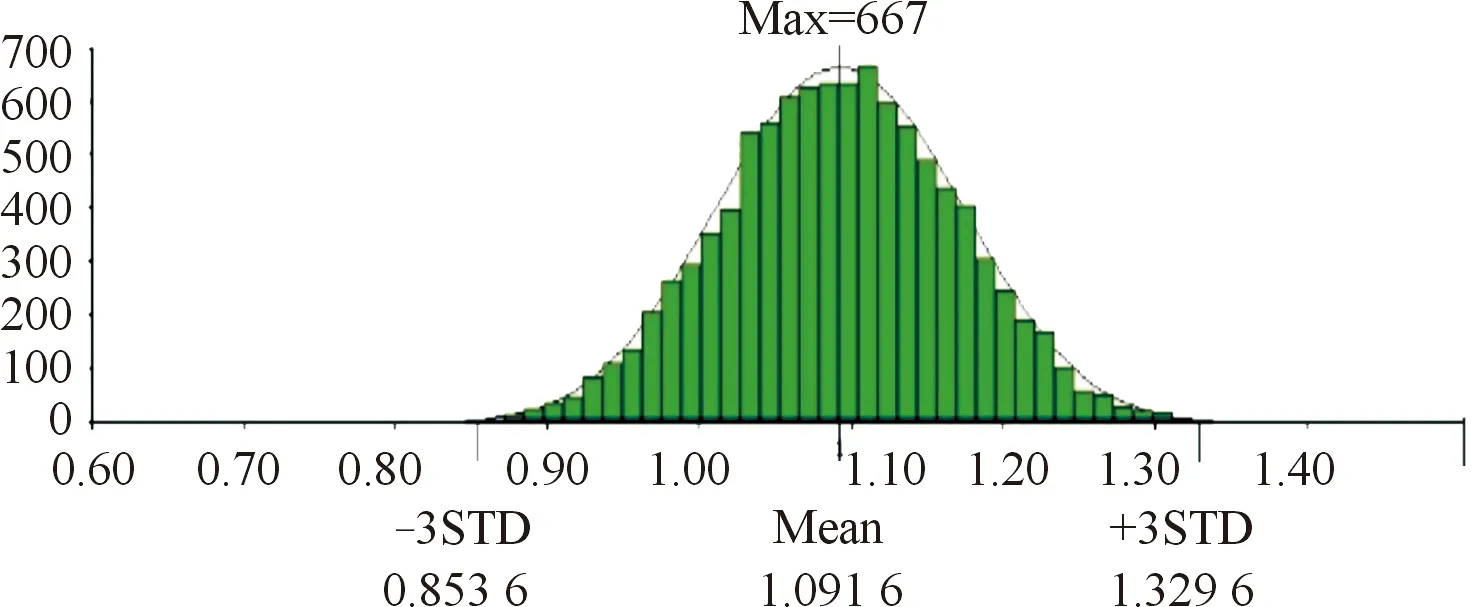
图13 模拟10 000次的叠盖量尺寸分布直方图Fig.13 Overlay size distribution histogram of 10 000 simulations

图14 模拟20 000次的叠盖量尺寸分布直方图Fig.14 Overlay size distribution histogram of 20 000 simulations

2.3.5组成环贡献度的求解

贡献度分析[15]是求解组成环公差输入变量对封闭环公差输出变量的影响大小的一种方法。贡献度分析计算采用单变量分析,首先对所有组成环变量值设为0,通过每次只变化单个组成环变量来分析目标的变化,从而确定该组成环的贡献度大小,该方法又称为HLM(high-low-median)贡献度分析。

HLM贡献度的计算方法与一阶导数的泰勒级数展开式有关,设输出参数m与输入参数ci的函数关系为:

m=f(ci),i=1,2,…,t(t为影响因子个数)

(18)

使用泰勒级数对式(18)展开为:

(19)

式中:m0即输出参数的名义值;Δc=ci-ci0表示输出参数的变化量。因为HLM贡献度分析是采用线性计算的方法,所以进行分析计算时需要将式(19)转化为线性函数:

(20)

分析模型时需要注意以下问题:① 所有的输入参数都应该满足相互独立的条件;② 输入参数的分布规律都假设服从正态分布,则输出参数的方差与输入参数函数关系为:

(21)

HLM贡献度的计算公式为:

(22)

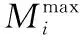
(23)

则贡献度公式为:

(24)

通过对封闭环的贡献度分析,将分析结果反馈给设计人员,可对组成环的公差进行相应的公差调整。图15为抛壳机构的贡献度分析结果示意图,其中封闭环精度影响因子最大的为机匣内左面与抛壳挺左侧面,均为30.92%,公差值大小均为0.075。在保证精度要求的前提下,通过调整贡献度较大的公差来最大化的降低成本,使得公差设计更加合理、有效。

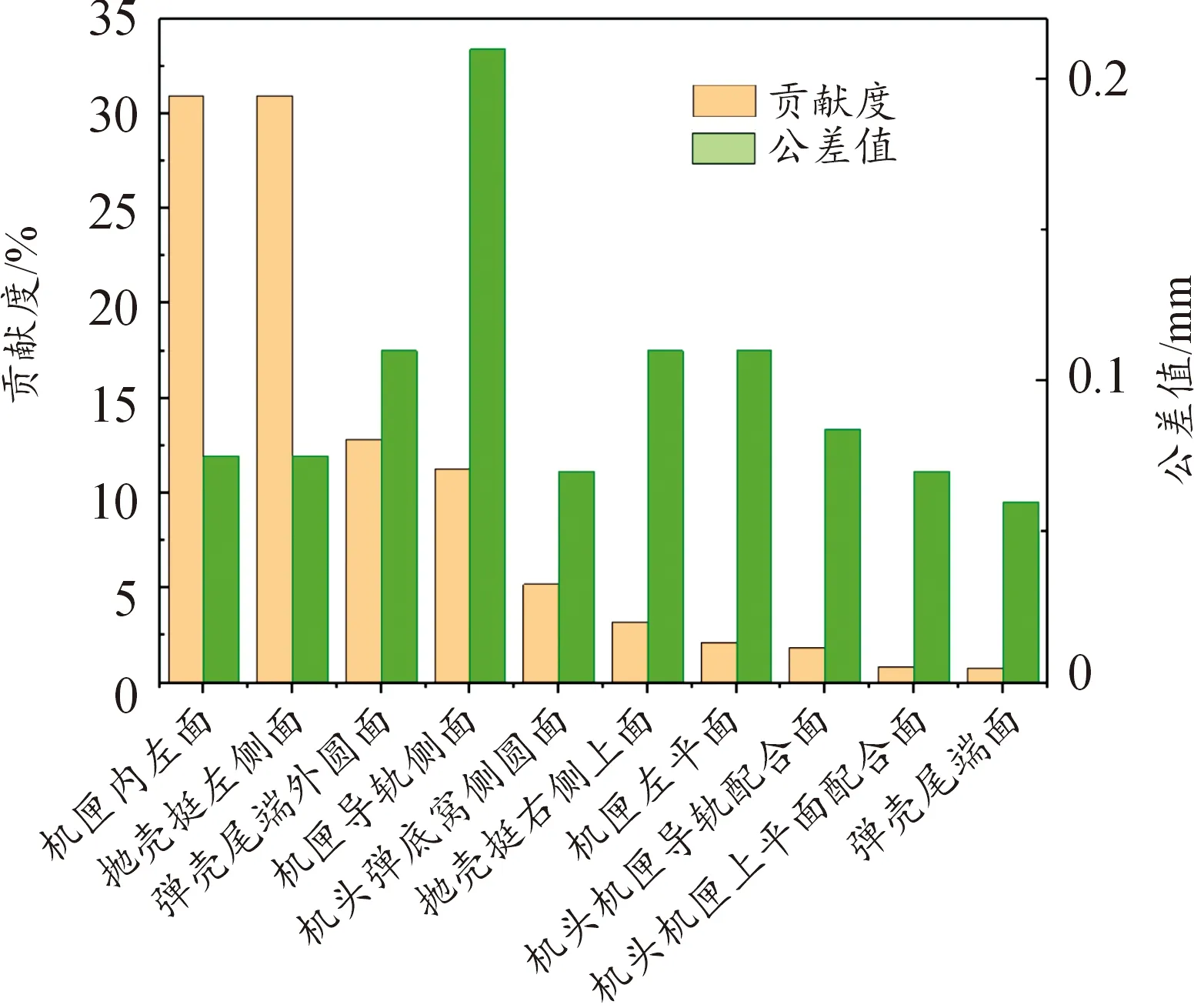
图15 各组成环公差贡献度分析Fig.15 Tolerance contribution analysis of each component ring

3 结果对比

为了体现基于SDT模型大和蒙特卡洛法的特点和优点,分别运用极值法和概率统计法求解出叠盖量的公差分析结果,并将三者进行数据对比分析,结果对比如表4所示。

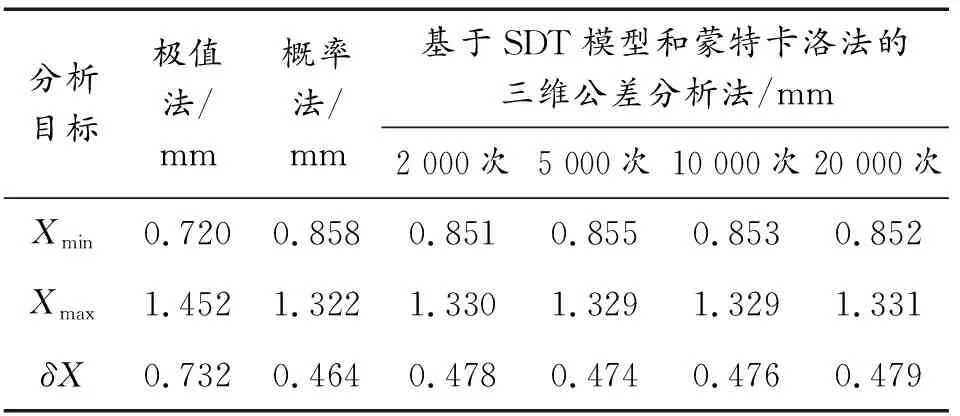
表4 3种公差方法结果对比Table 4 Comparison of results of three tolerance methods

基于SDT模型和蒙特卡洛法的三维公差分析四次模拟仿真求解的封闭环公差值约为0.477,小于极值法计算值0.732,稍大于概率法计算值0.464,但基本与概率法保持一致,结果具有可信度。该方法随着样本点的增多,尺寸分布直方图趋近于正态分布,与设计结果保持一致,在相同的尺寸公差水平下,可以根据贡献度分析结果,对相应尺寸公差进行优化宽松,加工经济性好,更符合实际加工生产,结果更具有可信度。该方法的应用可使枪械抛壳机构的装配成功率和质量可靠性得到较大的提升。

4 结论

本文采用了SDT模型对某枪械中抛壳机构进行公差参数化建模,并通过齐次坐标矩阵描述装配误差累积模型,结合蒙特卡洛法进行三维公差分析,得出抛壳机构中叠盖量的尺寸分布直方图和贡献度分析报告,并与传统的极值法和概率法公差计算结果进行了数据对比分析,验证了基于SDT模型和蒙特卡洛法的三维公差分析方法的有效性与精确性。

通过数据的对比可以得出,相比于传统的极值法和概率法,基于SDT和蒙特卡洛的三维公差分析方法可以将几何公差和尺寸公差用统一的模型来表示,且理论上其分析结果具有更高的精度,计算方便、快捷,且通过组成环贡献度分析更有利进行公差的分配和设计。该方法的应用不仅可以简化计算过程,而且能提高装配成功率,提高零部件的可靠性,降低生产成本,更能适用于生产实践。