基于自适应Fourier分解-同步提取变换的机械故障诊断方法
陈子慧,李志农,谷士鹏,程 娟
(1.南昌航空大学 无损检测教育部重点实验室, 南昌 330063;2.中国飞行试验研究院, 西安 710089)
0 引言
同步提取变换(synchroextracting transform,SET)是于刚等[1]在同步挤压变换[2]中提出一种新的非平稳信号处理方法,通过提取时频脊线能量,有效提高时频分辨率,具有能量集中性好,抗噪能力强的特点,同时在摆脱海森堡不确定性原理影响的情况下,能有效构建信号的理想时频谱。目前,SET已在地震储层识别[3]、石油勘探[4]、引力波探测[5]、变速旋转机械[6]、结构瞬时频率识别[7-8]、机械故障诊断[9]、滚动轴承[10]等多个领域中获得了成功应用。此外,张春博[11]等将SET在时频分析中的高分辨率特征引入地震波吸收衰减分析技术中,实现油气藏的精准定位。孙秀秀[12]等将SET用于高铁轨道波磨检测与定位,解决有效检测轨道波磨问题。胡志峰[13]将SET方法应用于微弱故障的特征提取和增强。然而,现有的同步提取变换存在一些不足,如在处理强噪声干扰情况下,传统SET方法不能有效提取故障信号的时频信息,SET算法本身存在误差,当随机噪声较低且谐波幅值较大时,SET重构信号引起误差超过随机噪声。此外,SET方法要求各相邻分量瞬时频率需满足相邻模态的瞬时频率差大于所选取的SET窗函数频率支撑范围的2倍。而在实际的工程应用中,分析的信号不一定能满足上述条件。为了发挥SET处理非平稳非线性时聚效果好的优势,克服其不足之处,有必要对传统的SET方法进行改良。针对多分量信号,进行信号分解有助于去除信号冗余,提取有用信息。而传统的分解方法如EMD适用于非平稳信号,但存在包络误差、端点效应及模态混叠的问题[14],经验小波分解针对接近模态的信号,存在无法分解部分频率的问题[15],变分模态分解方法具有自适应性,但是需要预设模态个数和惩罚参数,无法分解重叠频谱[16]。自适应傅里叶分解 (adaptive Fourier decomposition,AFD)算法是基于钱涛先生[17]所创立的一种基于单分量函数理论的新的傅里叶转换,其收敛性和表征的瞬间频率都要高。AFD算法对给定信号应用AFD可以得到基本信号的级数展开,称为单分量,采用最大功率选取原则对原始信号进行优化,使得重建后的信号保持了原有的振荡特性[18],同时,AFD算法重构信号的信噪比SNR大大提高,从而使得对该信号进行了更好地解析[19]。AFD方法能有效地处理一维和多维的数据。在实际信号分解过程中, AFD方法根据不同的功能,所产生的单个成分也各有差异,且其频率从高到低依次递增,此外,由于其不负的解析相微分,以及等效的分析和有效的瞬态频率,使其保持了较好的数理特性[20]。同时,在相同误差下,AFD运行时间短。目前,AFD在多通道的信号分析[21]、柔性薄壁轴承[22]、非平稳无限信道的时频快速变化为代表的信道函数重构[23]等领域达到较好的效果。基于AFD的高效分解的独特优势,本文将自适应Fourier分解引入到机械故障诊断中,并与同步提取变换相结合,提出一种新的AFD-SET方法,与传统的SET算法比较,并进行仿真和实验验证。本文提出的方法为有效解决频率接近的多分量信号混叠问题提供了一种有效方法。
1 AFD-SET方法原理
提出的AFD-SET方法的基本思路是:首先用AFD方法对采集的振动信号进行自适应分解,基于能量最大选择原则选取接近原信号能量值的单一分量进行自适应重构,再对该信号进行SET方法处理,得到瞬时频率特征信息。该方法特色在于可以解决SET在处理相邻信号分量的瞬时频率需满足相邻模态的瞬时频率差大于所选取SET窗函数的频率支撑范围的2倍的问题。接下来对该方法进行详细阐述:
AFD涉及在H2(∂D)空间中给定信号G(t)的自适应分解,D表示复平面中以原点为心的开单位圆D{z∈C∶|z|<1},并且C是复平面,成为一系列单一分量fk(t),k为分解次数。
fk(t)=bkBk(z),k=1,2,…,n
z=eit=cos(t)+isin(t)
(1)
其中,
bk=Gk(t)·eak(z)
(2)
(3)
(4)
(5)
式中:e为指数;Bk(z)为有理基函数;z为单位圆的边界值,其模等于1。Gk(t),k=1,2,…,n是给定的振动信号G(t)自适应分解而产生的变量,G1(t)=G(t);bk为Gk(t)与eak(z)内积运算结果。
首先设定初始值a1=0,ak根据最大投影原理计算,
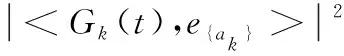
(6)
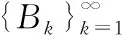
(7)

重复上述过程,则可以得到振动信号G(t)的所有单一分量f1(t),f2(t),f3(t),…,fk(t)。
接着自适应对上述单一变量重构,得到重构信号G′(t)
G′(t)=Aeiω0t
(8)
最后,对重构信号进行短时傅里叶变换处理,得到短时傅里叶变换的时频系数G(t,ω)
(9)
式中,g(u-t)为高斯窗函数。
在短时傅里叶变换的时频系数中增加一个频移算子e-iωt,得到Ge(t,ω),
(10)
此时Ge(t,ω)不为零。再与同步提取算子(狄拉克delta函数)相乘,从而得到了同步提取变换时频的时频系数Te(t,ω):
Te(t,ω)=Ge(t,ω)·δ(ω-ω0(t,ω))
(11)
对关于时间求偏导,计算瞬态频率,
(12)
其中,当Ge(t,ω)不为0时,在任意时间范围内,满足[ω0-Δ,ω0+Δ]内瞬时频率数值为恒定值ω0,其中Δ为同步提取变换窗函数的频率支撑范围。ω0(t,ω)为瞬时频率,据此可表征二维瞬时时频。
基于AFD-SET的轴承故障诊断算法主要分为2个部分。一是对信号的分解,然后是对故障特征频率的提取。基于AFD算法的信号分解可得到一系列频率由低到高的单一分量,对其基于最大能量选取原则对部分单一分量重构再进行同步提取变换处理。对应的轴承故障诊断算法流程如图1所示。
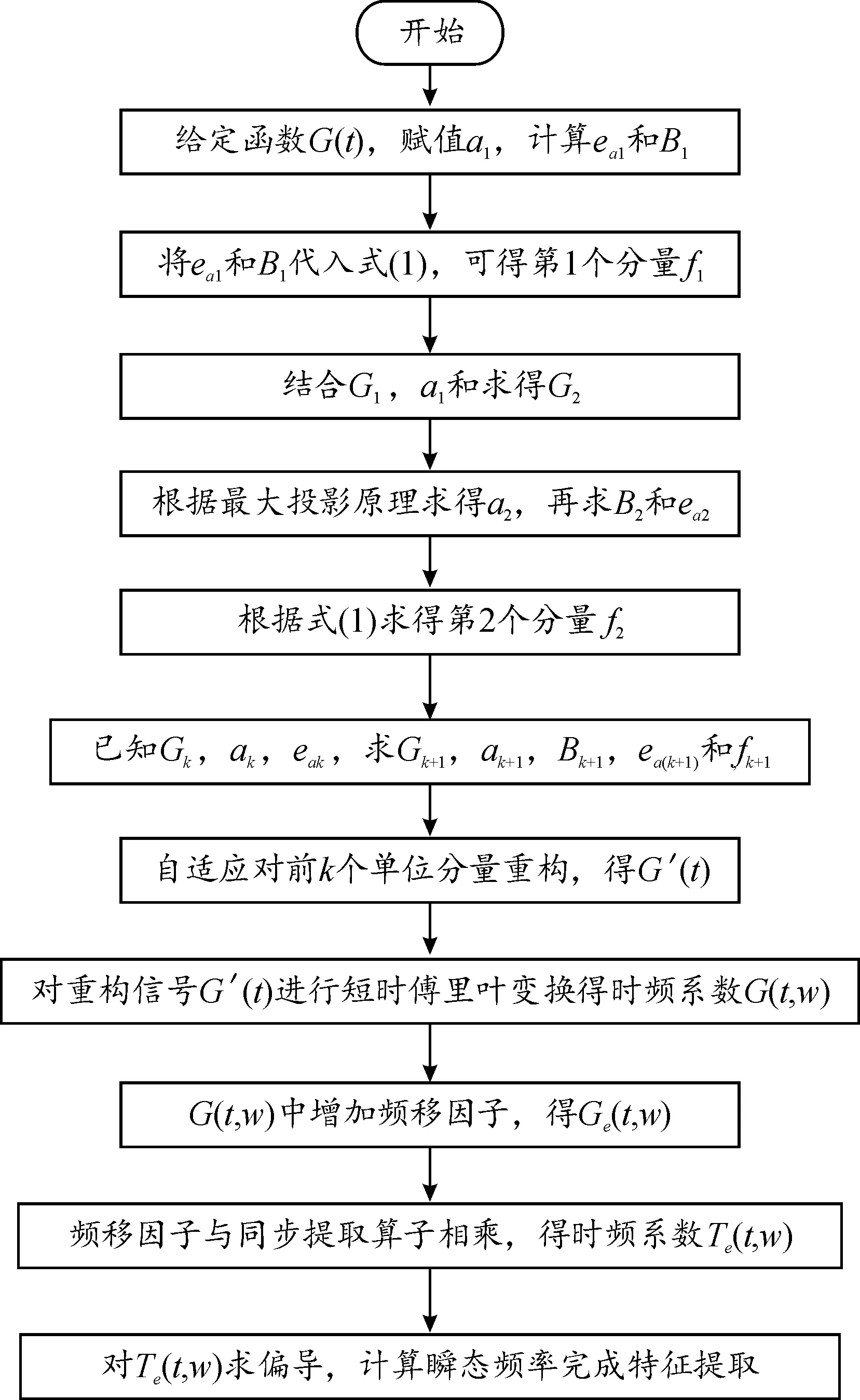
图1 基于AFD-SET轴承故障诊断流程图Fig.1 Flow chart based on AFD-SET bearing fault diagnosis
2 仿真研究
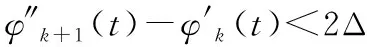
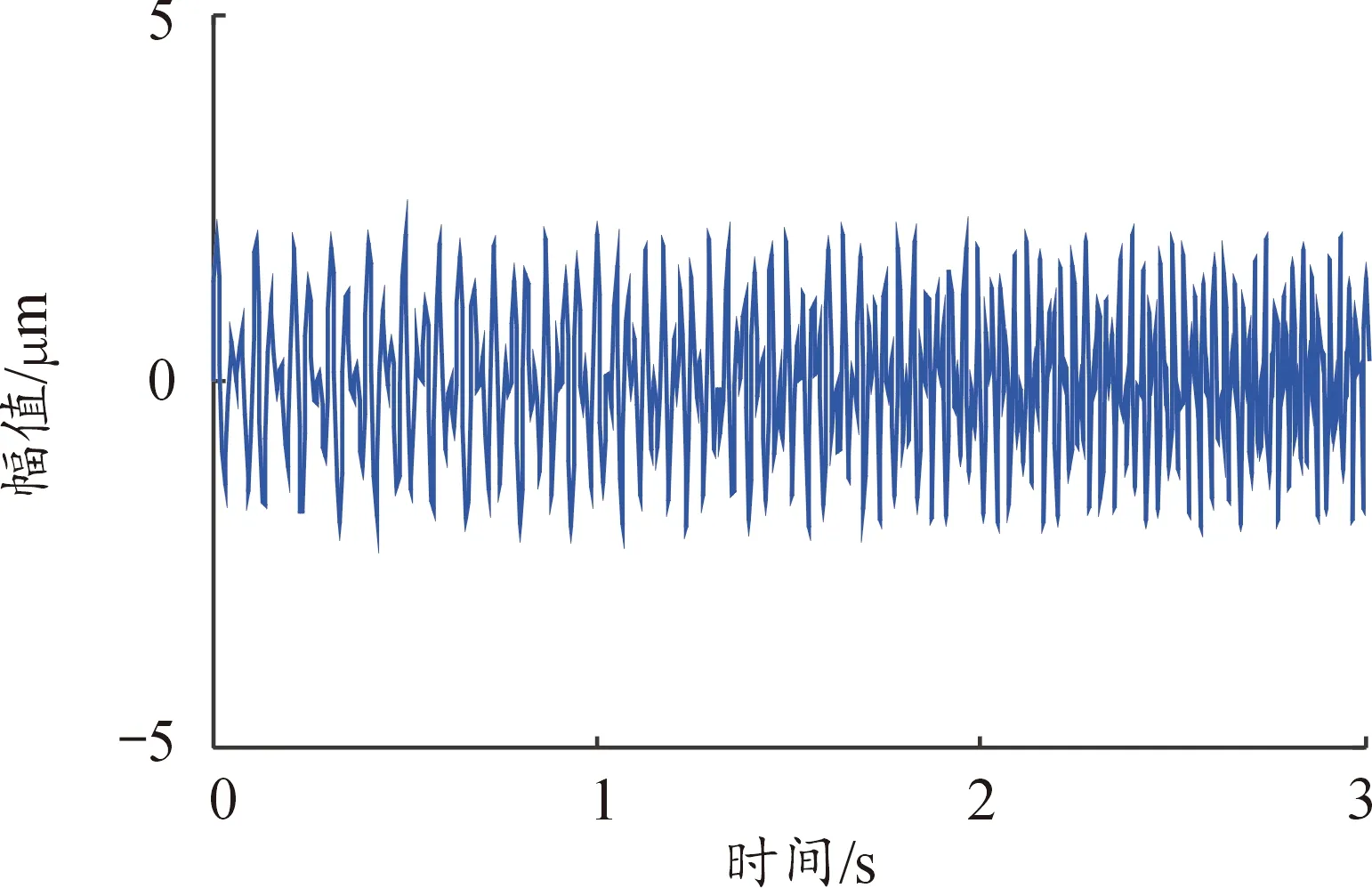
图2 信号G(t)的时域图Fig.2 Time domain waveform of signal G(t)
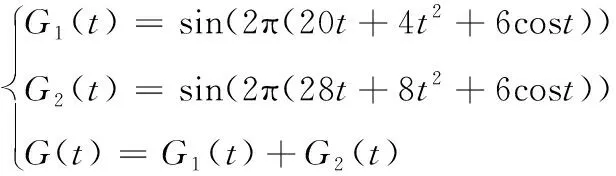
(13)
首先对该仿真信号采用传统的SET方法处理,结果如图3所示。
由图3可知,时间由开始到1.13 s时,两分量存在较近的瞬时频率,在使用传统的SET方法时,两瞬时频率中间出现了频率混叠的现象,曲线中间出现虚假频率。这是因为传统SET方法处理多分量非平稳复杂信号时,各相邻分量瞬时频率不满足相应条件。
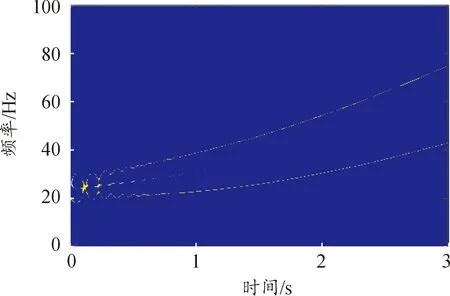
图3 传统SET方法Fig.3 Traditional SET method
接着对仿真信号进行AFD-SET处理,AFD算法选取单分量的原则是逐项最佳,使得部分和在能量上最大限度接近原函数,综合考虑选取分解层数为200层,将能量差最小的单分量进行自适应重构信号的时域图如图4所示。

图4 重构信号的时域图Fig.4 Time domain waveform of reconstructed signals
相比于原始信号,重构信号滤除噪声影响,且较好地反映了原信号的时域特征。然后将重构信号进行AFD-SET处理,结果如图5所示。
观察图5,对重构信号进行AFD-SET处理,时频图未出现频率混叠,能准确识别两分量的瞬时频率。当信号各相邻分量瞬时频率不满足相邻模态瞬时频率差大于所选SET窗函数频率支撑范围的两倍时,AFD-SET能有效抑制时频混叠现象,相比传统SET方法,时频更清晰,具有明显的优势。
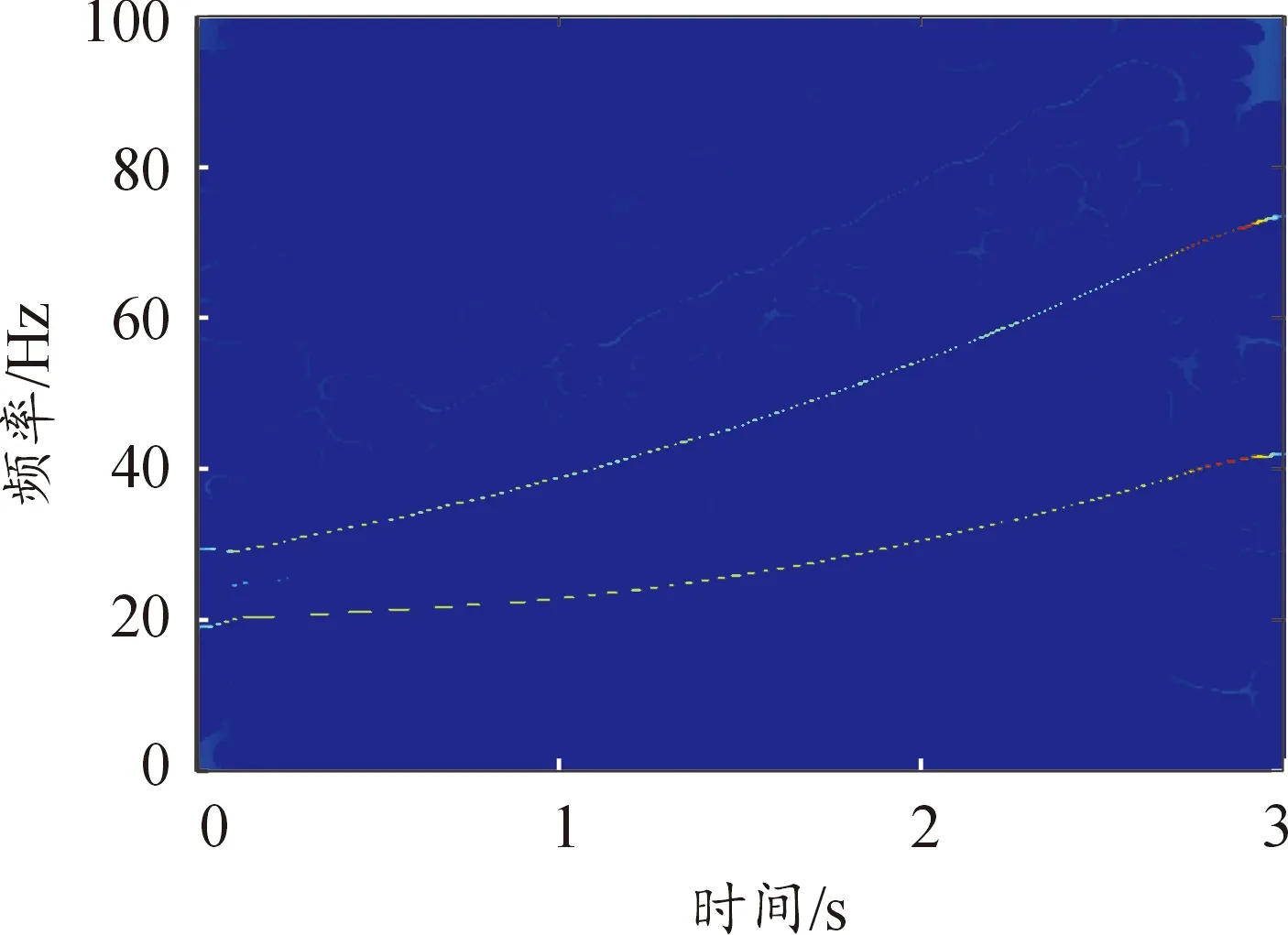
图5 AFD-SET方法Fig.5 AFD-SET method
为了进一步验证方法的有效性,在原有基础加入信噪比为20db的噪声,并进行AFD处理得到波形如图6所示。
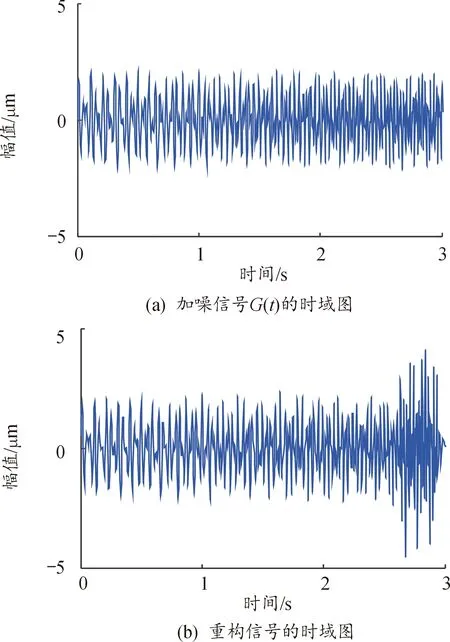
图6 加噪信号的AFD处理Fig.6 AFD processing of the noisy signals
接着对加噪信号分别进行SET、AFD-SET方法处理,得到结果如图7所示。
由图7可知,加入高噪声之后,传统的SET方法出现更为严重的频率混叠,从0~1.13 s变为0~1.32 s的时间段。本文提出的AFD-SET方法对含噪声的信号处理,频率混叠程度大大降低,时频效果清晰可见,更有利于进行频率识别,体现了方法的优越性。
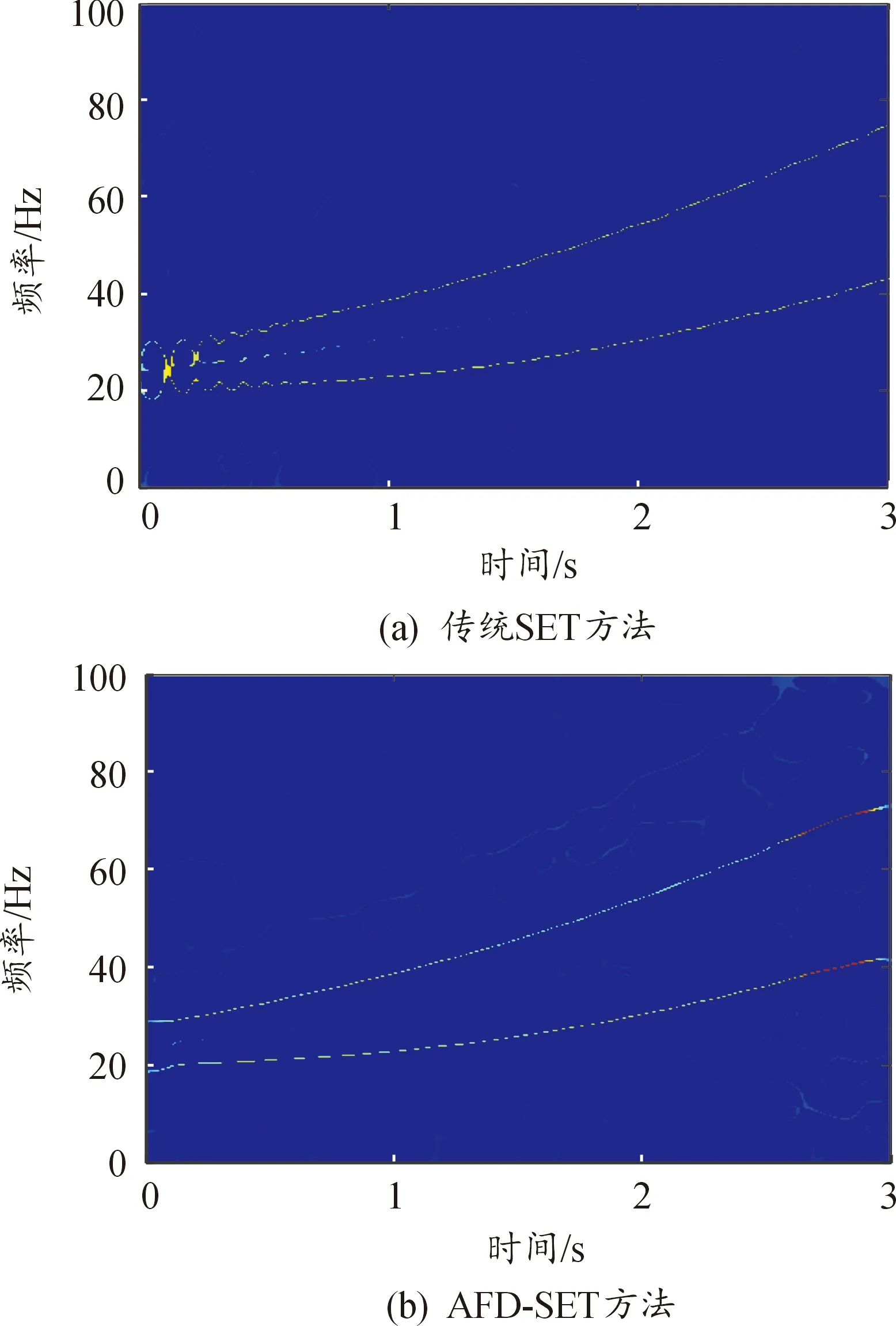
图7 信号G(t)的SET和AFD-SET方法比较Fig.7 Comparison of traditional SET method and AFD-SET method of signal G(t)
3 实验研究
为了进一步验证方法有效性,将AFD-SET方法应用到实验采集的振动信号特征提取中,采用的矿井提升试验台如图8所示[25]。故障为人工造成的表面细缝(宽2 mm,深1.5 mm),存在一定误差。轴承型号为ER-12k,采用的轴承规格为:滚动体直径为0.312 5英寸,轴承节圆直径1.318英寸,滚动体个数8个。将SET应用到实验采集的振动信号特征提取中,轴承振动信号用加速度传感器采集,采样频率为2 kHz,电动机转频为36 Hz,可计算得出内圈故障特征频率178.2 Hz。

图8 矿井提升实验台Fig.8 Mine hoisting test bench
为了得到故障特征频率的变化,对实验信号进行时频分析。内圈故障的原始信号时域图见图9所示。

图9 原始信号时域图Fig.9 Time domain waveform of signals
实验中选取分解层数为200层,自适应重构信号的时域信息见图10所示。观察图10,重构信号接近于原始信号,且滤除了噪声干扰。

图10 重构信号时域图Fig.10 Time domain waveform of reconstructed signals
将原始信号及AFD后重构的内圈故障信号分别采用SET方法进行分析,得到的时频分布如图11所示。
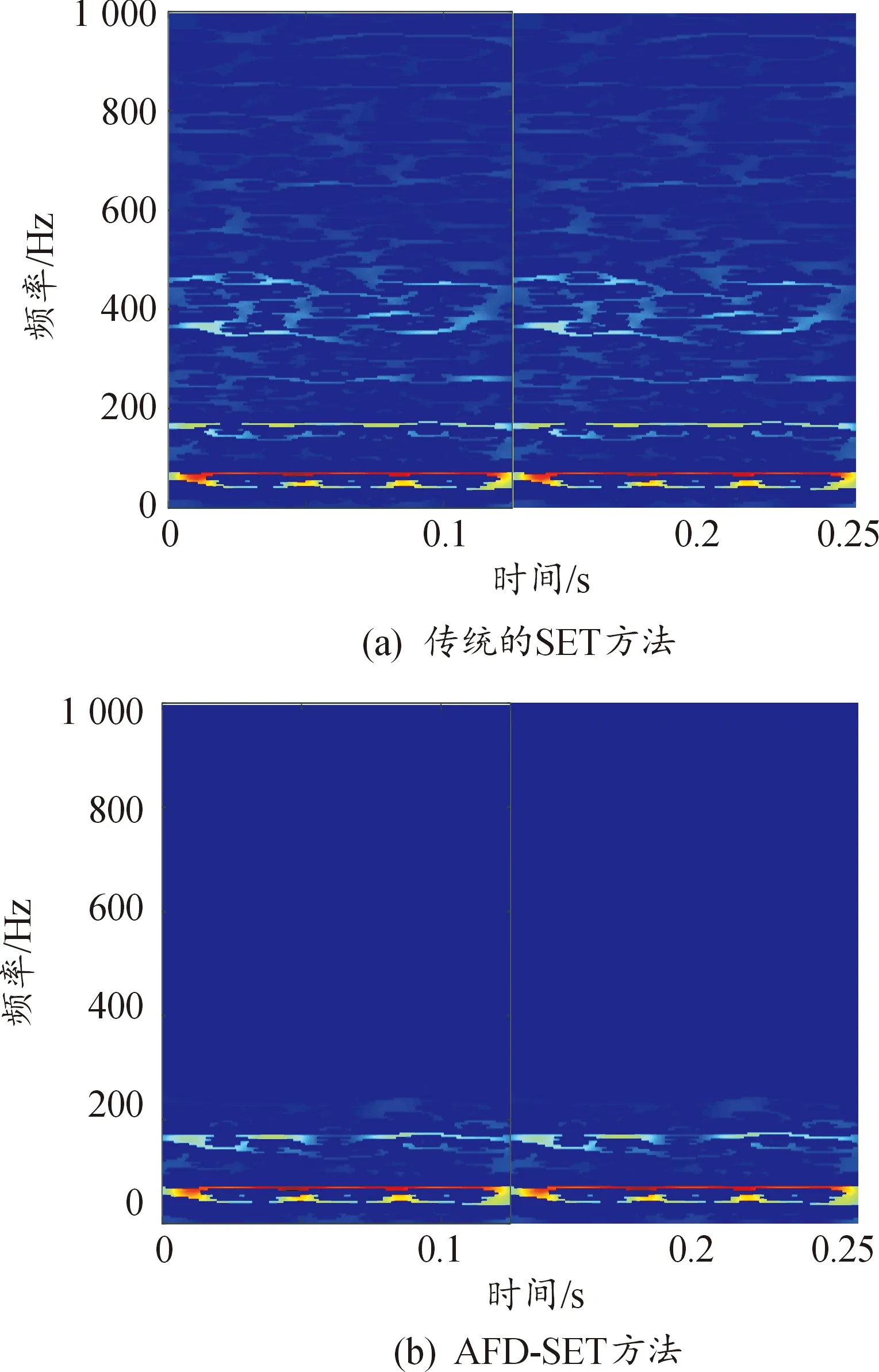
图11 信号的SET和AFD-SET方法比较Fig.11 Comparison of traditional SET method and AFD-SET method
由图11可知,针对内圈故障信号,传统的SET方法得到的信号的频谱图中还含有大量杂频,这些难解释的频率会影响故障诊断,而AFD-SET方法能有效提取出故障频率,低幅值区域内信号中的杂频成分减少。这主要是因为AFD算法的独特优势,AFD有着滤除与轴承故障无关的冲击成分并消除了部分背景噪声的作用,即增强信号中的故障特征。
观察时频图,信号中的杂频成分都得到了较好地抑制,相应的故障特征频率谱线变得更加明显,在图中明显反映了滚动轴承内圈故障特征频率178.2 Hz,同时,电机转频36 Hz也明显反映出来,所提方法有效地识别出故障频率,且抑制了高频率噪声的干扰,时频聚集性较好。
4 结论
本文针对传统SET方法处理频率成分临近信号时的时频分析能力不足的问题,引入一种新颖的信号分解方法(即AFD方法)构造出AFD-SET方法,并与传统的SET方法进行比较。由仿真和实验可知:
1) 在多分量信号不满足相应条件的情况下,AFD-SET方法能有效抑制传统的SET方法中存在的频率混叠现象,并具有一定的抗噪性能,有效地提取了信号的时频分布特征。仿真结果验证了提出的方法比传统的SET方法具有明显的优势。
2) 将提出的AFD-SET方法应用到矿井提升机的滚动轴承故障实验中,提出的方法能够有效识别轴承故障特征,与传统的SET方法比较,提出的方法提取的故障频率谱线更加突出,时频分辨率表现更优越,能准确识别滚动轴承的故障特征频率。

