“最多”与“最少”的启示

杜永宁

《义务教育课程标准（2022版）》指出：“教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系。”如何体现数学学科本质呢？就是要抓住概念、原理、方法之间及数学意义的相通性、一致性。“一致性”为核心素养落地提供了新视角，它反映的是学科本质，教学中应该慎思之，笃行之。

笔者用下面的教学实践来见证思考“一致性”的必要和乐趣。

西南师大版数学四（下）有关于“求最大（小）”的这样一个例题：小剧院共有甲票座位50个，票价30元，乙票座位100个，票价10元。本场票房收入为2300元。本场观众最少有多少人？如果仅仅从“人数最少，就应该是票价高的甲票尽量多卖”出发来解决问题，学生只是掌握了一个“孤立”的题目，他们无法理解这个问题来自何方，去向何处，学习价值将大打折扣。这个问题的数学本质在哪儿？它与哪些数学问题是相通的呢？

我首先想到了“票房（销售）收入”。所以我设计了一个准备题：小剧院共有甲票座位50个，票价30元，乙票座位100个，票价10元。一场演出满座，本场票房收入有多少元？学生解答后，我引导学生列出数量关系：甲票单价×甲票张数＋乙票单价×乙票张数=票房收入。

接着谈话：现实生活中，并非每场都能满座，你看这一场情况就是……接着出示例题。学生认识到，现在是知道了票房收入，反过来计算售票总张数。那就需要知道售出的甲票张数和乙票张数分别是多少（老师在之前数量关系处记上问号）。接下来学生讨论，根据“人数最少”确定下来先“尽量多售出票价高的甲票”，即先把50张甲票全部售出。学生结合数量关系上的标注解答此题。

到达这一步，学生起码知道原来例题是由“求总收入”的问题变身而来，而利用“两积求和”的数量关系也可进一步理解自己解答方法，关键是“人数最少”把其中“一个积”确定了下来。

我没有停下来，而试着让学生更深刻一些。所以，我出示了下面的练习：小剧院共有甲票座位50个，票价30元，乙票座位100个，票价10元。本场演出票房收入为2300元。观众人数可能是多少？

我引导学生把数量关系改写成：30×□＋10×□=2300，现在甲票张数和乙票张数都是不确定的了（这就是个“不定方程”），又该怎么解答呢？解答时有什么技巧呢？

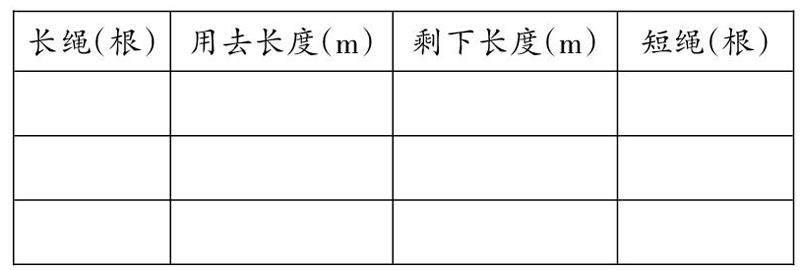
这时，我请学生回看了一张二年级下期的教材图片，第一个题目是：一根长绳4米，一根短绳2米。用一条10米长的绳子来做这两种跳绳，可以怎么做？

学生恍然大悟，原来二年级就碰到过这样的问题。于是，枚举法自然派上了用场，枚举的技巧也在讨论中应运而生。

原来例题的问题真是来源于不定方程，只是在特定条件下，“不定”变成了“确定”。

当教师站在“一致性”的视角思考，学生学习的每个内容就不会孤独。有了教师的“一致性”思考，学生每天都在一点一点地构建自己的知识结构网。这样的学习才深刻而有意义。