基于聚类质量的两阶段集成算法

闫晨　杨有龙　刘原园

摘要： 针对现有的集成聚类算法通常默认使用K-means算法作为基聚类生成器， 虽能确保聚类成员的多样性， 却忽视了差的基聚类可能会对最终聚类结果造成极大干扰的问题， 提出一种基于聚类质量的两阶段集成算法. 鉴于K-means算法运行高效但聚类质量较粗糙， 提出首先在生成阶段采用K-means算法生成基聚类成员， 然后通过群体一致性度量筛选出兼具高质量和强多样性的聚类成员， 形成候选集成； 其次， 进一步在集成阶段应用信息熵知识构建基聚类加权的共协矩阵; 最后应用一致函数得到最终聚类结果. 采用3个指标在10个真实数据集上进行对比实验， 实验结果表明， 该算法在有效提升聚类结果准确度的同时， 能保持较好的鲁棒性.

关键词： 集成聚类； 聚类质量； 群体一致性； 信息熵； 一致函数

中图分类号： TP391 文献标志码： A 文章编号： 1671-5489（2023）04-0899-10

Two Stage Ensemble Algorithm Based on Clustering Quality

YAN Chen， YANG Youlong， LIU Yuanyuan

（School of Mathematics and Statistics， Xidian University， Xian 710126， China）

Abstract： Aiming at the problem that existing ensemble clustering algorithms usually used K-means algorithm as the base clustering generator， although it could ensure the diversity of clustering members， it ignored that poor base clusterings might cause terrible disturbance to the final clustering result， we proposed a two stage ensemble algorithm based on clustering quality. Considering that K-means algorithm ran efficiently， but the clustering quality was relatively rough， firstly， we proposed to  use K-means algorithm to generate base clustering members in the generation stage， and then  selected clustering members with both high quality and strong diversity through  group aggrement measure to form candidate ensemble. Secondly， the information entropy knowledge was futher applied to construct the weighted-clustering co-association matrix in the ensemble stage. Finally， the final clustering result was obtained by using consensus function. Three indexes were used for comparative experiments on ten real datasets， and the experimantal results show that the algorithm can effectively improve the accuracy of clustering results while maintaining good robustness.

Keywords： ensemble clustering; clustering quality; group aggrement; information entropy; consensus function

聚類作为数据挖掘中的一种常用算法， 能发现未知数据的潜在模式， 进一步指导实践， 在机器学习、 数据挖掘和人工智能等领域应用广泛［1-5］. 聚类的基本思想是根据相似性或距离的大小将数据划分为若干类， 再利用人工对各类指定类别， 从而便于将数据价值最大化. 目前已有很多非常成熟的聚类算法［4-5］， 但这些算法通常仅能处理特定类型的数据， 且对参数的依赖性过高， 导致聚类效果不佳且应用范围较窄.

集成学习［6］是机器学习领域中一种非常重要的技术， 其通过一定规则融合多个模型的结果， 期望得到一个更好的结果. 集成学习主要分为集成分类和集成聚类. 集成聚类［6］的主要思想是融合多个“好而不同”的聚类结果， 得到一个精度和鲁棒性都更强的聚类结果. “好而不同”是指基聚类成员之间应满足本身的聚类质量较好， 同时彼此之间的差异性较大的条件， 以确保能得到一个更好的一致聚类结果. 集成聚类的这一优越性能使得它可以在很大程度上克服单个聚类算法的缺陷， 进一步拓宽了聚类的应用.

集成聚类算法可分为生成基聚类和集成基聚类两个阶段. 目前对集成聚类算法的研究主要关注两个问题： 一是如何生成“好而不同”的基聚类成员； 二是如何设计集成策略. 对于第一个问题， 一般采用启发式算法， 包括在数据层面对样本或特征加入扰动， 算法层面对同一算法设置不同参数或采用不同算法生成基聚类成员. 由于谱聚类对小样本具有良好的分簇能力， 因此可降低谱聚类的计算复杂度［7-10］， 使其应用于大规模数据集. 对于第二个问题， 目前的研究主要分为基于相似度的集成聚类算法和基于图模型的集成聚类算法. 尽管现有的集成聚类算法已取得了较好的效果， 但仍存在两个问题： 1） 多数算法默认使用K-means算法作为基聚类生成器， 然后考虑聚类的效率和多样性， 但忽视了其中差的基聚类可能对最终结果造成极大干扰， 研究表明， 在保证基聚类质量的前提下尽可能增强其多样性， 有利于得到一个更好的集成结果［11-13］; 2） 在设计集成策略时常平等地对待所有基聚类或同一基聚类内的所有簇， 缺乏对集成信息的深入探索.

针对上述问题， 本文提出一种基于聚类质量的两阶段集成算法. 首先采用K-means算法生成若干多样化的基聚类成员， 然后利用群体一致性度量计算每个基聚类的质量， 从中筛选出排名靠前的质量与多样性都较好的基聚类， 将其作为集成阶段的候选成员， 再进一步在集成阶段利用信息熵估计基聚类质量， 构造融合基聚类质量的共协矩阵， 最后对该矩阵应用层次聚类算法得到最终聚类结果.

1 相关工作

在对集成聚类算法的相关研究中， 基于相似度的方法和基于图的方法是两种主流的研究方法. 基于相似度的方法将集成信息表示为一个共协矩阵， 每个元素表示样本对在所有基聚类中同时出现的频率， 然后把该矩阵视为相似矩阵， 再应用任何一种划分算法得到最终的聚类结果. 这类方法概念简单， 可解释性强， 且易于实现和聚合， 因此受到广泛关注. Fred等［14］提出了共协矩阵的概念， 并进一步提出了证据累积聚类（evidence accumulation clustering， EAC）， 但该方法平等地对待参与集成的每个基聚类， 忽视了不同基聚类的质量差异对最终结果的影响. 针对上述缺陷， Wang等［15］将每个基聚类的簇规模和样本维数考虑在内， 对EAC方法进行改进， 提出了一种概率累积的方法， 从而能更好地度量样本之间的成对相关性. Huang等［16］提出以群策智慧思想估计基聚类质量， 之后又提出了利用信息熵估计不同簇对集成的贡献度， 得到改进的局部加权共协矩阵［17］. 考虑到共协矩阵中存在部分不确定样本对， 可能会影响聚类效果， Yi等［18］提出通过设置合理的阈值， 从共协矩阵中去掉不可靠样本， 再利用矩阵补全技术完全化共协矩阵， 最后应用谱聚类得到划分结果. 由于共协矩阵本身并不能涵盖全部集成信息， 因此Zhong等［19］提出从共协矩阵中多次移除部分低频共现元素， 对形成的多个矩阵分别进行聚类并设计了一个内部度量， 根据该度量选择聚类质量最好的一个作为最终集成结果. Zhou等［20］利用子空间聚类思想， 结合微簇概念， 通过构造目标函数， 优化学习后得到一个代表点级别上的相似矩阵， 划分后得到聚类结果.

基于图模型的方法将集成聚类问题转化为图分割问题， 进而得到聚类结果. 这类算法的关键在于如何构图， 包括如何设置图节点以及如何定义边权重. Strehl等［21］最早提出了3种基于图的算法， 分别是基于样本相似度的算法（cluster-based similarity partitioning algorithm， CSPA）、 超图划分算法（hyper graph partitioning algorithm， HGPA）和元聚类算法（meta-clustering algorithm， MCLA）. CSPA以样本为图节点， 根据共协矩阵定义样本权重构造图； HGPA以簇為超边， 每条超边连接了所有属于该簇的样本； MCLA以簇为图节点， 对两个簇计算Jaccard系数并作为边权重建立元图. 由于HGPA算法在构图时可能会丢失部分数据信息， Fern等［22］对其进行了改进， 把样本和簇同时作为图节点， 若样本属于某个簇， 则它们之间的边权重为1， 否则为0， 提出了一种混合二部图描述算法. 为充分利用集成信息， Huang等［23］通过在图上进行随机游走， 提出了概率轨迹累积聚类和概率轨迹图划分算法; 并结合类簇在集成中的不确定性， 构造出融合簇可靠性的局部加权二部图［17］. 此外， 还有一些针对谱聚类的改进算法［24-25］， 可以应用于较大规模数据集或者高维数据集.

上述这些算法均重点关注集成方法的设计， 默认使用K-means算法生成基聚类成员， 无法为集成阶段提供一个良好的输入， 从而影响最终聚类效果. 根据机器学习界公认的GIGO（garbage in， garbage out）原理， 即差的前提导致差的结论， 本文提出对集成聚类算法的两个阶段分别采用不同方法控制基聚类质量， 以提升聚类的准确度.

w（πm）表示样本xi和xj所属基聚类的权值. 把这个共协矩阵A′视为相似矩阵， 进一步应用层次聚类算法进行划分得到最终聚类结果.

根据上述对算法过程的描述， 本文设计了一种基于聚类质量的两阶段集成算法（two stage ensemble algorithm based on clustering quality， TSEC）， 从全局角度考虑基聚类质量， 期望聚类准确度能有所提升.

算法1 TSEC算法.

输入： 数据集X， 采样率r%， 簇数k， 集成规模M;

输出： 聚类结果;

步骤1） 利用K-means算法生成T个基聚类， 将结果表示为N×T阶矩阵D；

步骤2） 对矩阵D随机降采样， 取r%个样本的聚类结果， 构成一个新的N×T阶矩阵E；

步骤3） 对矩阵E进行标签重排， 得到新矩阵F；

步骤4） 基于矩阵F， 根据式（1）和式（2）计算所有基聚类的质量， 从大到小排列后选择前95%的基聚类作为基聚类池；

步骤5） 从基聚类池中随机取M个基聚类进行集成；

步骤6） 根据式（3）和式（4）计算每个基聚类对集成的不确定性；

步骤7） 根据式（5）计算每个基聚类在集成中的权重；

步骤8） 根据式（7）得到改进的共协矩阵A′；

步骤9） 应用层次聚类算法得到最终的集成聚类结果.

3 实验结果与分析

为验证本文算法的有效性， 设计4组实验. 第一组实验为确定采样率； 第二组通过消融实验验证加入降采样方法对最终结果的贡献度； 第三组实验， 将本文算法与7个集成聚类算法在3个指标上进行性能对比； 最后测试本文算法对集成规模的鲁棒性. 为保证实验结果的公平、 公正性， 所有实验均在Intel（R） Core（TM） i7-6700 CPU @3.40 GHz 3.41 GHz， Windows 10， MATLAB 2020a上完成.

3.1 数据集与评估准则

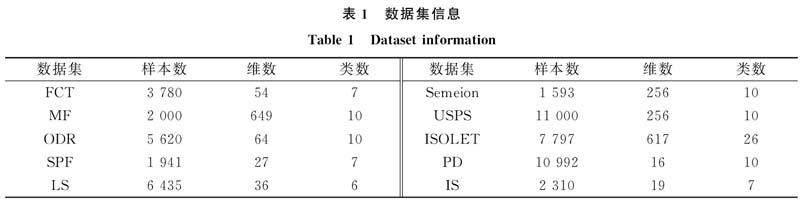
本文使用10个真实数据集进行实验， 分别是FCT（forest covertype），MF（multiple features），ODR（optical digit recognition），SPF（steel plates faults），LS（landsat），Semeion，USPS，ISOLET，PD（pen digit）和IS（image segmentation）. 除數据集USPS来自文献［17］外， 其他数据集均来自UCI机器学习库， 各数据集信息列于表1.

本文所有对比算法的基聚类池均由K-means算法在［2，N］内变换簇数， 生成100个基聚类构成. 为证明本文算法的性能， 采用标准互信息、 调整兰德系数（adjusted Rand index， ARI）和准确度（ACC）3个指标衡量聚类效果. 这3个指标值均为越接近1， 则聚类效果越好.

3.2 TSEC算法采样率的确定

分别设置3个不同采样率（10%，30%，50%）考察采样率大小对本文算法准确度和运行时间的影响， 以证明加入降采样的TSEC算法在生成阶段设置采样率为10%， 通过随机降采样方法估计基聚类质量的合理性. 对每个采样率， 设置算法的集成规模为20， 记录其运行30次的平均ACC值及运行时间， 结果分别如图1和图2所示.

由图1可见， 对于在不同采样率上的平均ACC值， TSEC算法只有在数据集FCT，SPF和IS上略有变化， 在其余7个数据集上该算法的平均ACC值基本相等. 由图2可见， 算法运行时间随着采样率的增大而增大. 此外， 数据量和维数的大小也会影响算法的运行效率. 综合考虑算法在不同采样率下的准确度和运行成本， 本文选择采样率为10%.

3.3 消融实验

为验证加入降采样方法对TSEC算法的贡献度， 本文设计一组消融实验. 对比算法与本文算法的不同之处在于前者直接基于生成的基聚类集合计算基聚类质量， 未采用降采样方法. 对比算法称为不加降采样方法， 两种算法均设置集成规模为20， 运行30次后分析各自的平均ACC值及运行时间， 结果均保留至小数点后4位. 由于两种算法在不同数据集上运行时间的差异在于生成阶段采用NGAM度量计算基聚类质量这一部分， 因此只记录该部分的用时. 两种算法在所有数据集上的实验结果列于表2.

由表2可见， 在FCT，ODR，LS和ISOLET 4个数据集上， 加降采样方法的ACC值略高于不加降采样的方法. 其中， 在FCT数据集上本文提出的加降采样方法的准确度提高了2.43%. 在其余数据集上， 两种方法的ACC值几乎相等， 相差范围在0.002～0.005. 但显然加降采样方法的运行速率更高效， 在10个数据集上， 运行效率提高了120%～750%. 特别是在数据集PD，USPS和ODR上， 运行效率分别提高了748%，450%和574%. 因此， 相比于不加降采样的方法， 本文提出的加降采样的TSEC算法在保持准确度相当的情况下可大幅度提速， 突出了在生成阶段对基聚类成员集合先随机降采样再去筛选基聚类的重要性.

3.4 集成规模的鲁棒性分析

选择数据集FCT，MF，ODR和LS测试TSEC算法与其他对比算法在不同集成规模下的鲁棒性. 实验设置集成规模为10～30， 步长为5. 对每个数据集， 所有算法在不同集成规模下各自运行30次， 记录平均NMI、 平均ARI和平均ACC值， 结果如图3所示.

由图3可见， 当集成规模为20时， TSEC算法在数据集FCT，MF和ODR上的NMI值高于其他对比算法. 对5个集成规模， TSEC算法在数据集FCT，MF，LS上的ARI值均优于对比算法. 其中， 在数据集FCT上， 当集成规模为20时， TSEC算法的ARI值达到最大. 对数据集MF， TSEC算法的ARI值在集成规模大于20后逐渐趋于平稳. 在数据集LS上， TSEC算法的ARI值随着集成规模的增大而增大. 对于ACC值， TSEC算法在选用的4个数据集上的性能均优于对比算法， 且ACC值随着集成规模的增加而逐渐趋于稳定. 综合TSEC算法在4个数据集上关于3个指标的性能， 兼顾算法运行成本， 本文选择集成规模为20.

3.5 与其他集成聚类算法的对比实验

为进一步验证本文算法的有效性， 将TSEC算法与其他7个先进的集成聚类算法进行对比实验. 对比算法为3个图聚类算法， 分别是概率轨迹图划分（probability trajectory based graph partitioning， PTGP）算法、 多粒度连接图划分（graph partitioning with multi-granularity link analysis， GPMGLA）算法和局部加权图划分（locally weighted graph partitioning， LWGP）算法， 以及4个基于共协矩阵的算法， 分别是证据累积聚类（EAC）、 概率轨迹累积（probability trajectory accumulation， PTA）聚类、 加权证据累积聚类（weighted evidence accumulation clustering， WEAC）和局部加权证据累积（locally weighted evidence accumulation， LWEA）聚类. 实验设置所有算法的划分数目均为数据集真实类数， 集成规模为20. 记录每种算法在不同数据集上运行30次的平均NMI、 平均ARI和平均ACC值， 结果分别列于表3～表5. 所有实验结果均保留至小数点后4位.

由表3可见， 与性能次优的算法相比， TSEC算法在数据集FCT，MF，ODR，USPS和ISOLET上的NMI值都有小幅度提高， 提高范围为0.19%～2.12%. 在其余5个数据集上本文算法的性能略差， 相比于性能最佳的算法， TSEC算法的NMI值落后范围为0.8%～7.75%. 由表4可见， TSEC算法在FCT，MF，ODR，SPF，LS，USPS和ISOLET数据集上的ARI值性能较好. 特别是在数据集LS上， 与性能次优的PTA算法相比， TSEC算法的ARI值提高了5.31%. 由表5可见， 与对比实验相比， TSEC算法的ACC值总体上性能较好. 尤其是在数据集SPF上， 相比性能次优的LWGP算法， TSEC算法的ACC值提高了10.81%. 此外， 与性能次优的PTA算法相比， TSEC算法在数据集LS上的ACC值也提高了7.16%. 在数据集FCT，MF和USPS上， 相比于性能次优的算法， TSEC算法的ACC值分别提高了3.09%，2.65%和3.01%.

根据上述分析， 虽然TSEC算法在数据集PD和IS上的NMI值和ARI值略逊于LWEA和LWGP算法， 但效果相差较小. 此外， 由表3～表5可见， PTA算法在多个数据集上性能良好， 这可能是因为PTA算法通过连接可靠节点， 在图上根据概率轨迹随机游走获取全局结构信息， 有效提升了聚类性能. 因此， TSEC算法在3个指标上的聚类效果总体上相对较好.

综上所述， 针对当前集成聚类算法研究侧重于集成策略的设计， 在生成阶段默认使用K-means算法生成基聚类成员， 仅能确保多样性， 忽视了基聚类质量对最终聚类结果影响的问题， 本文提出了一种基于聚类质量的两阶段集成算法， 采用不同度量方法对集成聚类算法的两个阶段分别把控聚类质量， 得到一个精度和鲁棒性都更好的聚类结果. 将本文算法与7个先进的集成聚类算法在10个数据集上进行对比实验， 实验结果表明， 本文算法可有效提高聚类准确度， 并保持较好的鲁棒性.

参考文献

［1］ZOU Q， LIN G， JIANG X P， et al. Sequence Clustering in Bioinformatics： An Empirical Study ［J］. Briefings in Bioinformatics， 2020， 21（1）： 1-10.

［2］OTTO C， WANG D， JAIN A K. Clustering Millions of Faces by Identity [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2017， 40（2）： 289-303.

［3］AGHABOZORGI S， SHIRKHORSHIDI A S， WAH T Y. Time-Series Clustering： A Decade Review [J]. Information Systems， 2015， 53： 16-38.

［4］OYELADE J， ISEWON I， OLADIPUPO O， et al. Data Clustering： Algorithms and Its Applications ［C］//2019 19th International Conference on Computational Science and Its Applications. Piscataway， NJ： IEEE， 2019： 71-81.

［5］GAN G J， MA C Q， WU J H. Data Clustering： Theory， Algorithms， and Applications [M]. Philadelphia： Society for Industrial and Applied Mathematics， 2020： 1-448.

［6］ZHOU Z H. Ensemble Methods： Foundations and Algorithms ［M］. New York： CRC Press， 2012： 135-155.

［7］HUANG D， WANG C D， WU J S， et al. Ultra-Scalable Spectral Clustering and Ensemble Clustering ［J］. IEEE Transactions on Knowledge and Data Engineering， 2019， 32（6）： 1212-1226.

［8］白璐， 赵鑫， 孔钰婷， 等. 谱聚类算法研究综述 [J]. 计算机工程与应用， 2021， 57（14）： 15-26. （BAI L， ZHAO X， KONG Y T， et al. Survey of Spectral Clustering Algorithms [J]. Computer Engineering and Applications， 2021， 57（14）： 15-26.）

［9］尤坊州， 白亮. 關键节点选择的快速图聚类算法 ［J］. 计算机科学与探索， 2021， 15（10）： 1930-1937. （YOU F Z， BAI L. Fast Graph Clustering Algorithm Based on Selection of Key Nodes ［J］. Journal of Frontiers of Computer Science and Technology， 2021， 15（10）： 1930-1937.）

［10］薛红艳， 钱雪忠， 周世兵. 超簇加权的集成聚类算法 ［J］. 计算机科学与探索， 2021， 15（12）： 2362-2373. （XUE H Y， QIAN X Z， ZHOU S B. Ensemble Clustering Algorithm Based on Weighted Super Cluster ［J］. Journal of Frontiers of Computer Science and Technology， 2021， 15（12）： 2362-2373.）

［11］BREIMAN L. Random Forests ［J］. Machine Learning， 2001， 45（1）： 5-32.

［12］周志华， 陈世福. 神经网络集成 [J]. 计算机学报， 2002， 25（1）： 1-8. （ZHOU Z H， CHEN S F. Neural Network Ensemble ［J］. Chinese Journal of Computers， 2002， 25（1）： 1-8.）

［13］TUMER K， GHOSH J. Linear and Order Statistics Combiners for Neural Pattern Classifiers ［EB/OL］. （1999-03-20）［2022-02-01］. https：//arxiv.org/abs/cs/9905012.

［14］FRED A L N， JAIN A K. Combining Multiple Clusterings Using Evidence Accumulation ［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2005， 27（6）： 835-850.

［15］WANG X， YANG C Y， ZHOU J. Clustering Aggregation by Probability Accumulation ［J］. Pattern Recognition， 2009， 42（5）： 668-675.

［16］HUANG D， LAI J H， WANG C D. Combining Multiple Clusterings via Crowd Agreement Estimation and Multi-granularity Link Analysis ［J］. Neurocomputing， 2015， 170： 240-250.

［17］HUANG D， WANG C D， LAI J H. Locally Weighted Ensemble Clustering ［J］. IEEE Transactions on Cybernetics， 2017， 48（5）： 1460-1473.

［18］YI J F， YANG T B， JIN R， et al. Robust Ensemble Clustering by Matrix Completion ［C］//2012 IEEE 12th International Conference on Data Mining. Washington， D.C.： IEEE Computer Society， 2012： 1176-1181.

［19］ZHONG C M， HU L Y， YUE X D， et al. Ensemble Clustering Based on Evidence Extracted from the Co-association Matrix ［J］. Pattern Recognition， 2019， 92： 93-106.

［20］ZHOU J， ZHENG H C， PAN L L. Ensemble Clustering Based on Dense Representation ［J］. Neurocomputing， 2019， 357： 66-76.

［21］STREHL A， GHOSH J. Cluster Ensembles： A Knowledge Reuse Framework for Combining Multiple Partitions ［J］. Journal of Machine Learning Research， 2002， 3（12）： 583-617.

［22］FERN X Z， BRODLEY C E. Solving Cluster Ensemble Problems by Bipartite Graph Partitioning ［C］//Proceedings of the Twenty-First International Conference on Machine Learning. New York： Association for Computering Machinery， 2004： 36-1-36-8.

［23］HUANG D， LAI J H， WANG C D. Robust Ensemble Clustering Using Probability Trajectories ［J］. IEEE Transactions on Knowledge and Data Engineering， 2015， 28（5）： 1312-1326.

［24］LIU H F， LIU T L， WU J J， et al. Spectral Ensemble Clustering ［C］//Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： Association for Computering Machinery， 2015： 715-724.

［25］LIANG Y N， REN Z G， WU Z Z， et al. Scalable Spectral Ensemble Clustering via Building Representative Co-association Matrix ［J］. Neurocomputing， 2020， 390： 158-167.

（責任编辑： 韩 啸）

收稿日期： 2022-05-31.

第一作者简介： 闫 晨（1997—）， 女， 汉族， 硕士， 从事模式识别和数据挖掘分析的研究， E-mail： 2799702609@qq.com. 通信作者简介： 杨有龙（1967—）， 男， 汉族， 博士， 教授， 从事高维数据分析与应用的研究， E-mail： ylyang@mail.xidian.edu.cn.

基金项目： 陕西省自然科学基础研究计划项目（批准号： 2021JM-133）.