含缺陷压力管道极限承载能力分析

李招辉　王琪　陆晓峰　朱晓磊　顾付伟　王健

摘 要 提出一种含缺陷压力管道极限承载能力图像有限元分析方法，采用内压爆破实验进行验证。结果表明：重构模型与真实模型的几何结构参数最大误差不超过2.50%；数值模拟计算所得极限载荷与实验爆破压力的误差分别为0.559%、7.020%、5.710%，且数值计算结果略小于实验结果。

关键词 含缺陷压力管道 扩展有限元法 内压爆破实验 极限载荷 CT扫描 三维几何重构算法

中图分类号 TQ055.8   文献标识码 A   文章编号 0254?6094（2023）02?0140?08

压力管道广泛应用于石油化工、冶金、电力、核工业及海洋开发等领域，由于焊接、冲刷、腐蚀及机械损伤等原因，绝大多数管道会存在一定的缺陷，这极大地降低了管道的承载能力和安全性［1］，甚至会引起管道破裂从而引发严重的安全生产事故。因此，先进的无损检测技术以及含缺陷构件力学性能评价方法成为含缺陷压力管道长期、稳定、安全运行的重要保障［2，3］。

对含缺陷压力管道进行断裂力学评定和分析的一个重要内容就是结构极限分析。通过极限分析，可以确定压力管道在不同种类和损伤程度缺陷条件下对应的塑性极限载荷，从而评价其极限承载能力和安全性。针对含缺陷压力管道塑性极限载荷的求解方法主要有解析法［4］和有限元分析法［5，6］。然而在进行数值模拟时，裂纹的奇异特性对传统方法具有一定影响，故引入扩展有限元法（eXtended Finite Element Method，XFEM）以弥补传统方法的不足。目前，基于XFEM的含缺陷压力容器和管道的研究多以分析裂纹扩展规律为主［7，8］，不仅可以展示含缺陷压力管道的完整破坏过程，有效分析裂纹扩展，还可以准确预测含缺陷压力管道破裂压力［9～11］。实际上，管道缺陷具有随机性和复杂性，因此如何建立含真实缺陷形貌特征的几何模型成为影响该方法准确性的主要因素。

图像有限元法是一种CT扫描三维几何重构算法，可以获得含真实缺陷的压力管道几何模型，建立的数字化模型不仅能够真实、直观地反映出被检构件缺陷的分布形态和几何特征［12，13］，而且与CAE分析软件具有良好的兼容性和交互性，可以进行数值模拟与极限分析［14～16］。

笔者设计了一种基于CT扫描数据驱动的含缺陷压力管道极限承载能力图像有限元分析方法，通过对含缺陷压力管道进行CT扫描获得断层扫描图像，采用三维几何重构算法建立含真实缺陷的数字化几何模型，再基于XFEM方法對含缺陷压力管道的裂纹扩展过程进行仿真，最后用临界失稳扩展速率对含缺陷压力管道极限承载力进行判定，并将计算结果与实验结果进行对比。

1 实验

1.1 试样制备

实验用管道试样材料为304不锈钢，其力学性能如下：

弹性模量E 193 GPa

泊松比μ 0.29

屈服强度σs 215 MPa

抗拉强度σb 505 MPa

夏比冲击Akv 325 J

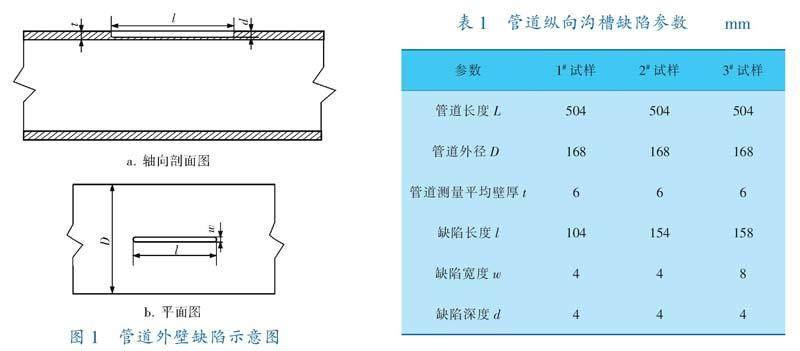
将压力管道的裂纹缺陷设计为轴向沟槽，采用车削加工方式预制缺陷（图1），缺陷参数见表1，含缺陷压力管道试样如图2所示。

采用工业CT扫描系统（GE Phoenix vltomelx 240）对含缺陷压力管道试样进行CT断层扫描实验。扫描参数具体如下：加速电压150 kV，电流250 μA，放大倍数14倍，投影数目1 000个，曝光时间19 min，积分时间1 000 ms，重建矩阵2048×2048。所得含缺陷压力管道CT扫描断层图像如图3所示（切片数量分别为1 100、1 700、1 700）。

1.3 内压爆破实验

全尺寸管道内压爆破实验是对含缺陷压力管道承压能力进行评价的最直接、有效的方法。设计工装夹具和应变片粘贴位置如图4所示。内压加载设备和数据采集系统如图5所示，内压加载设备为低流量柱塞泵，该泵配有一个压力表，可实时显示管道压力；数据采集系统为60通道的DH?3816N静态应变测试分析系统，用于采集加载过程中的管道表面应变值。

2 图像有限元分析方法

2.1 几何模型

用Avizo软件对含缺陷压力管道进行三维几何重构。

首先将断层扫描图像（图6a）导入软件，基于含缺陷压力管道的灰度特征，对其进行边缘锐化和二值化处理（图6b）；然后对二值化图像进行轮廓提取，并对表面进行重建，获得具有小平面特征的含缺陷压力管道曲面实体模型（图6c）；最后对小平面特征进行逆向工程，获得具有完整曲面特征的实体模型，并对曲面实体模型进行网格划分（图6d）。

2.2 边界条件

在扩展有限元分析过程中，将管道端部设置为固定约束边界条件，管道内壁面施加均布载荷P0。

2.3 网格划分

曲面实体模型整体网格划分均采用C3D8R连续实体单元。利用XFEM完成分析时，网格尺寸及初始载荷的大小对数值稳定性和计算精度有较大影响。根据文献［10］，可得到临界网格尺寸范围为：

式中 GC——相对临界能释放率，N/mm；

hm——裂纹扩展方向的临界网格尺寸，mm。

最终，得到1#、2#、3#试样的网格数分别为89 068、82 528、57 192。

2.4 扩展有限元前处理

选择Abaqus软件实现XFEM分析，其中有两个必要的前处理过程：

a. 选择模型中可能出现裂纹的区域，将其单元设置为具有扩展有限元性质的富集单元。所谓选择具有扩展有限元性质的富集区，即在软件的相互作用模块中直接设置，选择完整管道模型作为富集单元即可。

b. 选择合适的破坏准则，使单元达到条件时发生破坏，裂纹得以扩展。其中，破坏准则主要包括损伤起始准则和损伤演化准则。根据材料的力学性能，采用最大主应力准则为损伤起始准则；在损伤演化分析过程中选取基于能量、线性软化、混合模式的指数损伤演化规律，并采用B?K法则计算相对临界能释放率，因为裂纹扩展需要的能量由系统势能提供，裂纹扩展，裂纹表面积增加，系统势能下降，当裂纹扩展单位面积时，对应系统势能的下降量即为相对临界能释放率，并以此作为判断裂纹生成的边界条件，根据裂纹扩展区域的材料一致，取Ⅰ型裂纹、Ⅱ型裂纹、Ⅲ型裂纹具有相同临界能释放率，得到相对临界能释放率GⅠC=GⅡC=GⅢC=325 N/mm，能量系数α=1，损伤稳定系数为0.000 05。

3 结果与讨论

3.1 几何模型对比

为进一步验证含缺陷压力管道三维重建模型的可靠性，對重建模型的缺陷结构参数进行统计，结果列于表2。在表2可以看出，重构模型的几何尺寸与真实尺寸十分接近，外径最大误差为0.19%，壁厚最大误差为2.00%，缺陷长度最大误差为0.23%，缺陷深度最大误差为2.50%，缺陷宽度最大误差为2.25%。分析产生误差的主要原因是，试样在CT扫描过程中因缺陷部分厚度与无缺陷区域厚度有所差别，穿透缺陷狭缝产生干涉形成伪影，导致含缺陷三维重建模型与真实模型存在一定误差。

3.2 内压爆破实验结果分析

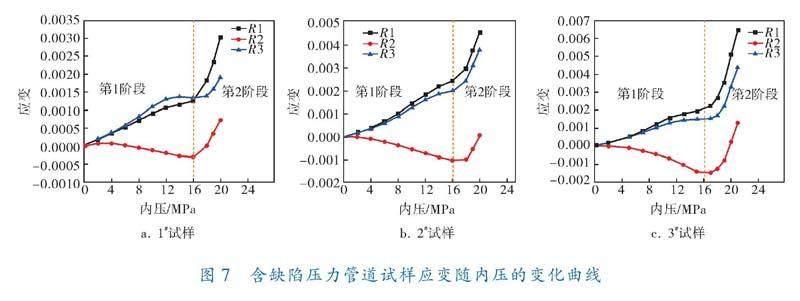
图7为含缺陷压力管道试样应变随内压的变化曲线，其中测点R1和R3用于测试缺陷前端的环向应变特征，测点R2用于测试缺陷中部的轴向应变特征。

由图7可以看出，含缺陷压力管道在内压载荷作用下，缺陷前端的应变特征主要分成两个阶段。第1阶段，随着内压载荷的增加，缺陷前端的环向应变逐渐增大，成线性关系。当内压载荷达到16 MPa时，随着内压载荷的继续增大，缺陷前端的环向应变特征进入第2阶段，应变随着内压载荷的增加急剧增大。这是因为内压载荷小于16 MPa时，测点R1和R3位置处于弹性变形阶段；当内压载荷大于16 MPa时，测点R1和R3进入塑性变形阶段，且塑性变形受缺陷影响较大。

测点R2的应变特征也呈现出明显的两个阶段。第1阶段，随着内压载荷的增加，测点R2处为压缩变形；这是因为在内压载荷的作用下管道发生径向膨胀，在材料破损效应的作用下，轴向发生压缩变形。当内压载荷达到16 MPa时，测点R2应变特征进入第2阶段，即随着内压载荷的增加，变形方式从压缩变形向拉伸变形转变；这是因为在缺陷的影响下，缺陷局部出现鼓胀，使得测点R2发生轴向拉伸变形。

含缺陷压力管道失效模式如图8所示，可以看出，3个试样的失效模式均为槽底断裂，且缺陷周围区域发生了明显的鼓胀变形。通过测试，含缺陷压力管道的爆破压力分别为20.05（1#试样）、20.98（2#试样）、22.78 MPa（3#试样）。

3.3 基于XFEM的极限承载力分析

采用基于CT扫描数据驱动的含缺陷压力管道极限承载能力图像有限元分析方法，分析内压载荷作用下不同含缺陷压力管道试样1#～3#的裂纹扩展过程，获得裂纹扩展速率与内压的关系如图9所示，第1阶段，裂纹扩展速率相对较快。原因是在内压载荷作用下槽底应力集中，根据最大主应力准则，当最大主应力超过505 MPa时萌生微裂纹，其裂纹扩展速率相对较快。该阶段最大主应力分布和裂纹扩展云图如图10所示。

图9中，第2阶段，随着内压载荷的增加，裂纹的扩展速率明显降低。这是因为随着内压载荷的增加，裂纹尖端发生塑性强化，导致裂纹扩展速率明显降低。

裂纹稳定扩展阶段的最大主应力分布和裂纹扩展云图如图11所示。

图9中，第3阶段为裂纹快速扩展阶段，即载荷超过某一临界值时，裂纹扩展速率极剧增加。这是因为当内压载荷达到裂纹扩展的临界失稳载荷时，管道剩余壁厚无法承受内压载荷，导致裂纹快速扩展，其最大主应力分布和裂纹扩展云图如图12所示。

由上述分析可见，含缺陷压力管道在内压载荷作用下，缺陷经历了裂纹萌生、稳定扩展和快速扩展3个阶段，裂纹达到快速扩展阶段所对应的内压载荷为含缺陷压力管道的极限承载内压。

基于上述方法，对含缺陷压力管道极限承载内压进行分析，并与实验结果进行对比，结果如图13所示。可以看出，3个试样的极限承载内压分别为19.938、19.508、21.480 MPa，与实验结果的误差分别为0.559%、7.020%、5.710%，且数值模拟结果略小于实验结果，具有一定的保守性，满足安全要求。

4 结论

4.1 基于CT扫描三维几何重构方法获得的含缺陷压力管道数字化模型，缺陷测量结果与试样测量结果相比，其几何特征尺寸误差最大不超过2.50%。

4.2 采用基于CT扫描数据驱动的含缺陷压力管道极限承载能力图像有限元分析方法，对含缺陷压力管道极限承载进行仿真分析，裂纹达到快速扩展所对应的内压载荷数值模拟值略低于实验结果，其误差分别为0.559%、7.020%、5.710%，满足工程使用要求。

参 考 文 献

［1］ 秦敬芳，陈定岳，陈文飞，等.含局部减薄缺陷压力管道的塑性极限载荷数值分析和安全评定研究［J］.化工设备与管道，2017，54（2）：74-77.

［2］ 侯文峰.无损检测技术在压力管道检验中的综合应用研究［J］.现代工业经济和信息化，2021，11（6）：142-144.

［3］ 肖思.弹塑性断裂及含缺陷脆性构件统一破坏准则研究［D］.北京：清华大学，2016.

［4］ AMAYA?GMEZ R，S?NCHEZ?SILVA M，BASTIDAS?ARTEAGA E，et al.Reliability assessments of corroded pipelines based on internal pressure—A review［J］.Engineering Failure Analysis，2019，98：190-214.

［5］   KIM N H，OH C S，KIM Y J，et al.Limit loads and fracture mechanics parameters for thick?walled pipes［J］.International Journal of Pressure Vessels & Piping，2011，88（10）：403-414.

［6］   KONG F T，WORDU A H.Burst strength analysis of pressurized steel pipelines with corrosion and gouge defects［J］.Engineering Failure Analysis，2020，108：104347.

［7］   陈星文.XFEM在高压管道裂纹扩展计算中的应用［J］.计算机辅助工程，2015，24（4）：56-60.

［8］   LIN M，AGBO S，CHENG J J R，et al.Application of the eXtended Finite Element Method （XFEM） to Simulate Crack Propagation in Pressurized Steel Pipes［C］//ASME 2017 Pressure Vessels and Piping Conference.2017.

［9］   LIU P F，ZHANG B J，ZHENG J Y.Finite Element Analysis of Plastic Collapse and Crack Behavior of Steel Pressure Vessels and Piping Using XFEM［J］.Journal of Failure Analysis and Prevention，2012，12（6）：707-718.

［10］   ZHA S X，LAN H Q.Fracture behavior of pre?cracked polyethylene gas pipe under foundation settlement by extended finite element method［J］.International Journal of Pressure Vessels and Piping，2021，189：104270.

［11］   OKODI A，LIN M，YOOSEF?GHODSI N，et al.Crack propagation and burst pressure of longitudinally cracked pipelines using extended finite element method［J］.International Journal of Pressure Vessels and Piping，2020，184：104115.

［12］   张文政，邱磊.基于CT三维重构的煤孔隙结构表征及分析［J］.煤炭技术，2018，37（12）：327-329.

［13］   CHATURVEDI A，BHATKAR S，SARKAR P S，et al.3D Geometric modeling of Aluminum based foam using micro Computed Tomography technique［J］.Materials Today：Proceedings，2019，18：4151-4156.

［14］   GENG L C，WU W W，SUN L J，et al. Damage char?acterizations and simulation of selective laser melting fabricated 3D re?entrant lattices based on in?situ CT testing and geometric reconstruction［J］.International Journal of Mechanical Sciences，2019，157-158：231-242.

［15］  LI Y Y，SUN B Z，GU B H.Impact shear damage characterizations of 3D braided composite with X?ray micro?computed tomography and numerical methodologies［J］.Composite Structures，2017，176：43-54.

［16］  RAM?REZ J F，CARDONA M，VELEZ J A，et al.Numerical modeling and simulation of uniaxial comp?ression of aluminum foams using FEM and 3D?CT images［J］.Procedia Materials Science，2014，4：227-231.

（收稿日期：2022-06-05，修回日期：2023-03-17）

Analysis of Ultimate Bearing Capacity of the Pressure Pipe with Defects

LI Zhao?hui1， WANG Qi2， LU Xiao?feng1， ZHU Xiao?lei1， GU Fu?wei1， WANG Jian1

（1. School of Mechanical and Power Engineering， Nanjing Tech University；

2. Special Equipment Safety Supervision Inspection Institute of Jiangsu Province）

Abstract   An image finite element analysis method for ultimate bearing capacity of the pressure pipe with defects was proposed. The results of internal pressure blasting test show that， the maximum error of the geometric structure parameter between the reconstructed model and the real model is less than 2.50%. The errors of the limit load calculated numerically and the experimental bursting pressure are 0.559%， 7.020% and 5.710% respectively， and the numerical calculation results are slightly smaller than the experimental results.

Key words   pressure pipe with defect， extended finite element method， internal pressure test， ultimate load， CT scan， 3D geometric reconstruction algorithm

作者简介：李招辉（1995-），硕士研究生，从事过程设备先进制造技术的研究，18851772938@163.com。

引用本文：李招辉，王琪，陆晓峰，等.含缺陷压力管道极限承载能力分析［J］.化工机械，2023，50（2）：140-147.