大学物理与高中物理光学部分的教学衔接研究

朱云龙　任永志　李玉祥

关键词 大学物理;中学物理;单缝衍射;半波带法;光程对称关系

高中物理对光学部分的教学和考察通常以几何光学为主、波动光学为辅，且在波动光学部分以定性了解为主、以定量分析为辅。以衍射为例，普通高中物理课程标准（2017年版2020年修订）选择性必修1中要求学生“观察光的干涉、衍射和偏振现象，了解这些现象产生的条件，知道其在生产生活中的应用”，但不要求学生定量分析衍射产生的明暗条纹位置[1]。

大学物理与中学物理不同，在光学部分重视波动光学，且以定量分析为主。由于普通高中物理课程标准对干涉部分的要求包括“会用双缝干涉实验测量光的波长”[1]，因此高中毕业生通常具有双缝干涉定量分析的基础;但从干涉向衍射的过渡涉及惠更斯菲涅耳原理的应用，具有一定的思维跨度，导致部分学生难以理解掌握衍射部分的授课内容。

帮助学生衔接高中物理知识并拓展其分析解决问题能力是大学物理教学的重要课题[2]。目前大学物理与高中物理光学部分的衔接已有相关研究发表[3]，然而其中教学衔接难度较大的衍射部分却未见具体的改进教学方案报导。本文以夫琅禾费单缝衍射的讲解为例，分析比对了目前大学物理中衍射的常见讲解方法，并利用光程对称关系对基于惠更斯菲涅耳原理的半波带法原理论证过程进行简化。这一教学方法课堂反馈良好，可以为大学物理教师以及有意拓展光学部分课外知识的中学物理教师提供参考。

1 夫琅禾费单缝衍射的常见讲解方法

夫琅禾费单缝衍射作为最基本的衍射模型，是衍射部分教学的要点。目前大学课堂教学通常采用的讲解方法包括惠更斯菲涅耳积分法、振幅矢量叠加法以及菲涅耳半波带法三种[4，5]。

惠更斯菲涅耳积分法是一种定量的分析方法，可以精确给出衍射光强表达式[6]。然而，通过积分推导明暗条纹位置的过程对于低年级本科生或课外拓展学习的高中生等授课对象而言难度较大，且物理图像不直观;此外，该方法讲解耗时较长，受限于授课时间安排，教师通常无法详细讲解积分过程。

振幅矢量叠加法的思想是将每个次波源所对应的光矢量首尾相接，当取的次波源尺寸趋近无穷小时，矢量首尾相接的曲线变为光滑的圆弧，计算合矢量振幅大小的极值即可准确获取明暗条纹位置[4，7-9]。该方法直观性上优于积分法，但推导的过程仍然较为复杂，且求解过程涉及超越方程，不适合高中生或低年级本科生的课堂授课。

与以上两种方法相比，菲涅耳半波带法更常见于衍射部分的授课过程中，因其物理模型与计算过程更为简洁、直观，也更易于被学生接受[10，11]。虽然菲涅耳半波带法的计算结果与惠更斯菲涅耳积分法之间存在一定的偏差[6，7]，但利用该方法却可在较短的时间内，使学生理解单缝衍射的基本原理，并掌握计算明纹与暗纹位置的方法。半波带法的主要不足之处为缺乏对于半波带模型合理性的定量剖析，可引起部分学生对于该方法科学性的质疑;若要剖析半波带法的原理，则只能引出授课时间较长、理解难度较大的惠更斯菲涅耳积分法或振幅矢量叠加法。下文将简要介绍夫琅禾费单缝衍射中半波带法的原理，并针对传统半波带法讲解过程中的不明晰之处给出一种新的教学思路。

2 夫琅禾费单缝衍射与半波带法

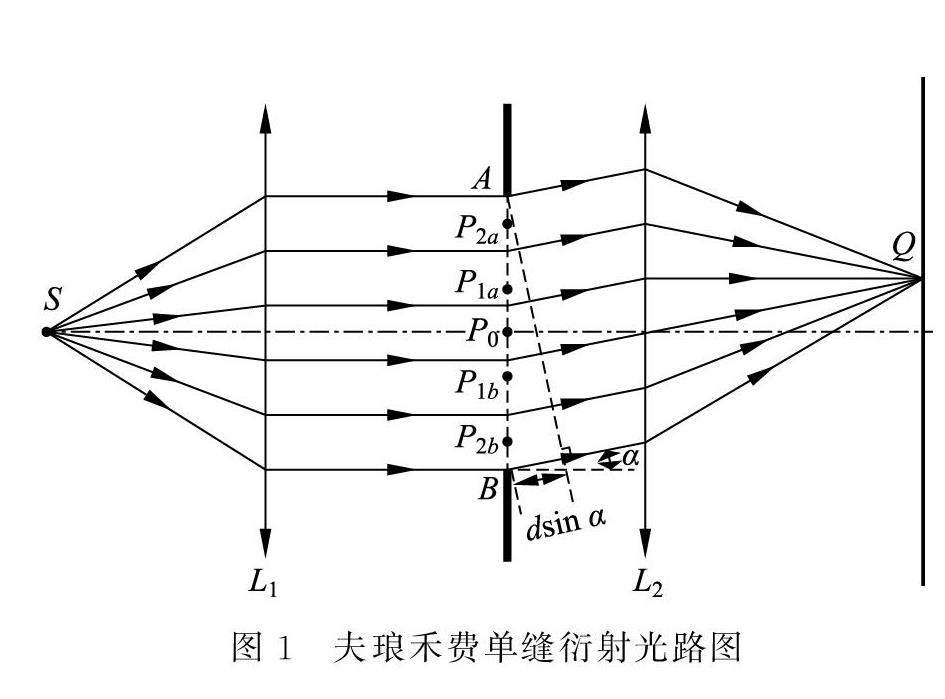
夫琅禾费单缝衍射的光路图如图1所示。点光源S 发出的单色相干光经凸透镜L1 扩束、准直后，经平行照射单缝AB。根据惠更斯菲涅耳原理，A 点与B 点之间的每个点都可视为次波的波源，且所有次波相干;入射光经过单缝后以水平方向夹角α 斜向上出射的部分经过透镜L2 汇聚于屏上Q 点，Q 点可发生相干增强或相干减弱，分别对应衍射明纹或暗纹。

设单缝AB 宽度为d，则B 点至Q 点的光程与A 点至Q 点的光程之间的差值δ 为

δ=dsina （1）

设入射光波长为λ，则当δ 为λ/2的奇数倍或0时，Q 点为相干增强的明条纹;当δ 为λ/2的偶数倍（不包括0）时，Q 点为相干减弱的暗条纹。该确定明暗条纹位置的方法，由于以半波长λ/2为参考因此被称为“半波带法”。半波带法虽然直观，但课堂上受限于学生基础与时间限制，一般只采用定性的解释，其原理剖析深度不足，会给学生对于该知识点的理解与记忆带来一定的困扰。

3 利用光程对称关系简化教学

对于低年级本科生或进行课外扩展学习的高中生而言，衍射的学习与理解通常具有较高难度，主要原因是理解衍射需引入高等数学中的微积分思想，将两个分量的干涉扩展为无数个子波源的干涉，因此普通高中物理课程标准只要求定性讲解衍射现象。

针对以上问题，为了高效完成从中学物理到大学物理关于夫琅禾费单缝衍射教学的衔接，本文基于半波带法，借鉴振幅矢量叠加法，根据光程对称关系提出一种新的教学方法。首先，将单缝处光场分解为无数振幅相等的子波源，根据惠更斯菲涅耳原理，可知所有子波源在屏上相干叠加形成衍射条纹。其次，围绕单缝中心点，根据光程对称关系，将每一对位置对称的子波源两两叠加，所获得光场相位均与单缝中心点子波源相位相同，但光场振幅均与特定数值相乘。最后，由于相位相同，屏上各子波源的相干叠加可转化为简单的数值叠加，根据所叠加数值的正负号特性，即可获得“当δ 为λ/2的奇数倍或0时，Q 点为相干增强的明条纹;当δ 为λ/2的偶数倍（不包括0）时，Q 点为相干减弱的暗条纹”这一定量结论，从而阐明半波带法的基本原理。

该讲解方法物理含义清晰，在大一年级大学物理教学的实践中获得了良好的效果;此外，该方法亦有助于学生快速理解后续教学内容中的光栅衍射缺级现象。该方法的具体原理如下文所述。

在图1中，假设单缝光强均匀，则单缝上任一微元的光场强度表达形式为

4 教学效果分析

本文所述的讲解方法从两个子波源之间的干涉入手，利用光程对称关系，结合三角函数和差化积公式或矢量相加性质，使微积分基础较弱的学生也能理解半波带法的原理与应用。在大学物理课堂实践中，只选取P₀，P_1a ，P_1b三點作为示例进行讲解，即可达到良好的教学效果。

2021年春季学期，在两个大一年级不同班级的大学物理线下授课实践中，采用板书的形式进行讲解，课堂反映良好。实际消耗时间约5分钟，对于课程进度的影响较小。此外，由于该方法将有宽度的单缝与宽度无穷小的单缝中心位置P0进行了等效处理，便于学生理解衍射光栅部分的缺级现象，故可在保证教学效果的同时，有效节约光栅部分的授课时间。

2022年春季学期，对两个大一年级不同班级进行大学物理线上授课，采用线上板书进行讲解，实际耗时同样约为5分钟。光学部分授课结束后，在学生群中发起无记名问卷，问卷覆盖了光学部分主要知识点的学习状况自评。收到学生填写完整的问卷共19份，其中与半波带法密切相关的为四道自我评分题，要求学生对于几个關键概念的掌握情况进行评分（根据掌握程度从低到高取0～10之间的整数），而且对于高中毕业时与学过大学物理光学部分后分别进行评分。针对相同学生、相同题目，将现阶段分数与高中阶段分数做差，可获得学生经过大学物理课堂学习后的进步分数。与半波带法密切相关的四道题目的问卷统计结果如表1所示。

提交的问卷中出现了个别问卷的个别题目进步分数为负的情况，可能由于学生填写时忙中出错造成。若将进步分数为负的题目作为异常数据排除，则可得到表1中“去除负数项平均”分数值;若考虑到学生填写问卷的认真程度，将包含负数项的整张答卷作为异常数据排除掉，则可得到表1中“去除负数答卷平均”分数值。由表1可知平均的进步分数约为3分，结合问卷填写耗时数据判断，出现负值大概率由于填写失误造成，因此“去除负数答卷平均”数据可靠性较高。

就“去除负数答卷平均”数据而言，可见学生对于自己的知识点掌握程度不满意，高中自评仅约1～2分，推测与高中物理中关于波动光学的讲解大多停留在定性层面、学生基础较为薄弱相关;学习过大学物理光学部分后，自评分数明显提升，但仅达到4～5分左右，推测与学生填写问卷时刚刚结束授课、复习尚未开始有关。“干涉的原理”与“衍射的原理”为半波带法的理论基础，而干涉的掌握情况略好于衍射，与高中物理干涉部分的讲解较为详细的实际情况相符。“光程/光程差的计算”为半波带法计算的数学基础，进步分数最高，推测与课堂上的重点讲授密切相关。“半波带法的理解”高中基础明显最为薄弱，但经过大学物理教学后获得了较为明显的提升，可见本文所述的教学方法有益于学生理解。“衍射的原理”部分进步分数高于“干涉的原理”，从侧面说明衍射部分的整体教学效果获得了一定提升。

5 结语

大学物理与中学物理有关光学部分的授课内容差异较大，主要体现为：中学物理侧重光学现象的定性解释、波动光学要求较低，而大学物理侧重光学现象的定量分析且波动光学要求较高。对于拓展课外知识、为学习大学课程做准备的高中生，或者微积分等数学工具运用不够熟练的本科生而言，大学物理光学部分具有较大的难度。大学物理教师授课时若忽视学生中学阶段较为薄弱的光学基础，则会使学生产生“断层”感，难以跟上学习进度;中学物理教师扩展光学部分内容时，若跨度太大，基本原理解释不清或不做解释，同样会使学生产生众多疑点。因此，教师应掌握并理解学生光学部分的水平，尤其是明确学生波动光学基础较为薄弱这一前提，进而设计适当的教学方法，逐步夯实基础，消除学生的疑点，实现大中衔接的平滑过渡。

在光学部分中，大学物理与中学物理对衍射的要求差异尤为明显，有必要设计一种既定量、又容易理解的讲解方式。本文以夫琅禾费单缝衍射为例，在学生对于光的干涉掌握情况较好、微积分基础较为薄弱的情况下，提出一种新的讲解方法，即：利用光程对称关系首先考虑子波源两两干涉的情况，从而在特定出射角将单缝等效为中心位置处宽度无穷小的窄缝，并建立光场叠加后的振幅与单缝宽度以及出射角之间关系，从而给出半波带法的物理解释。该方法讲解耗时较短、易于理解，且便于衔接光栅衍射等后续教学内容。在大学物理的线上以及线下教学实践中，该方法均获得了良好的教学效果。由此可见，物理教师应加强对于学生基础情况的了解，从而提出针对性更强的教学方法、提升课堂教学效果。