基于改进蚁群算法的全局船舶路径规划方法
黄国良,周毅,郑坤,李萌,蒙学昊
(中海油能源发展股份有限公司采油服务分公司,天津 300452)
路径规划算法性能的优劣将直接影响船舶航行的安全和效率。蚁群算法作为最常用的元启发式算法之一,在路径规划问题上取得了不错的效果,但仍然存在若干缺陷[1]:①容易陷入局部最优,且很难自主跳出;②初始信息素浓度分配方式和信息素更新规则没有针对性,不必要的探索会降低算法的收敛性。针对蚁群算法的两个主要问题,学者们提出了各种改进方法[2-8],但目前在船舶路径规划问题的求解中,普遍存在算法规划路径质量不高、收敛性与随机性无法保持平衡的问题。因此,考虑结合船舶路径规划的任务需求,采用启发式和融合式策略对蚁群算法进行改进。另外,将路径长度、安全性和平滑性约束函数融入至信息素更新规则,以保障船舶航行路径的安全。
1 蚁群算法数学模型
蚁群算法通过信息素浓度与距离启发函数计算蚂蚁选择路径的概率。假设蚁群中蚂蚁的数量为m,任意两路径点间的信息素数值相同。在n时刻,蚂蚁l=1,2,3,…,m从当前路径点i选择任意路径点j的概率为
(1)
式中:κ和λ分别是信息启发式因子和期望值启发式因子,Hij是距离启发函数,等于两路径点间欧式距离的倒数,Dl为路径点i下一时刻可选择的路径点集合。Iij为路径点i、j间的信息素数值。
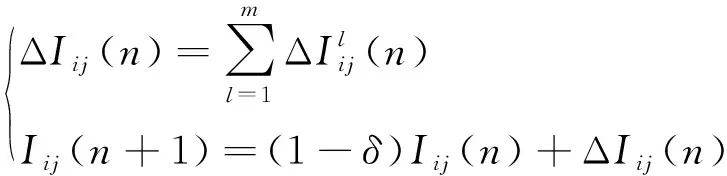
(2)

2 基于人工势场的改进蚁群算法
2.1 引入人工势场法
由于人工势场法具有初始导向性强、计算便捷和鲁棒性较强的特点,将人工势场法引入蚁群算法,提高蚁群算法的初始迭代速度。由于引力势场函数与本船到目的地的距离G的平方成正比,当G较大时会导致该点的引力值趋于无穷大,增加本船与碍航物发生碰撞的风险。为避免船舶与碍航物发生碰撞事故,设定引力势场函数影响分界线R。当G≤R时,使引力势场值与G的平方成正比;当G>R时,使引力势场值与G成正比,从而降低引力势场的影响范围。引力势场函数改进如下。
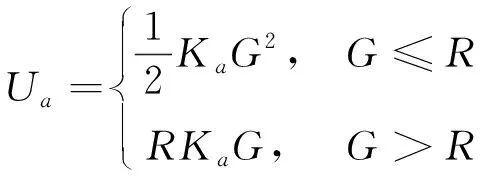
(3)
式中:Ka为引力势场系数。
2.2 伪随机状态选择概率的改进
传统蚁群算法以路径中信息素浓度和启发式信息函数的乘积作为路径选择概率。这种选择方式仅注重对新路径的搜索,常忽略对当前优秀路径的选择,易增加算法的时间复杂度。为此,引入随机数r与固定参数r0改进算法的选择概率。当r≤r0时,蚂蚁将启发式信息函数和信息素浓度乘积作为评价值,并选择使其数值最大的路径,即强化当前路径的选择;当r>r0时,选择基本蚁群算法的策略作为选择概率,即探索新路径。改进后的状态选择概率公式可使开发当前路径和探索新路径达到平衡,不仅能降低探索新路径产生的额外时间开销,还可避免过早的陷入局部最优。改进后的转移概率为
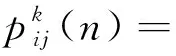
(4)
式中:r∈[0,1]为随机数;r0∈[0,1]为固定参数,r和r0的具体取值由人为设定。
2.3 信息素更新规则的改进
传统蚁群算法更新信息素时仅考虑了路径长度,而在解决实际船舶路径规划问题时,不仅要考虑路径长度,还要考虑路径安全性和路径平滑程度。因此,在信息素更新规则公式中加入路径的长度、安全性和平滑性目标约束,修改后的信息素公式更新为
(5)
式中:ω1、ω2、ω3是约束函数的权重系数;Il是蚂蚁l访问过的节点;Fl、Fs、Fm分别为路径长度、路径安全性和路径平滑度约束函数。
(6)
式中:t是路径上节点的总数量;d(i,i+1)为节点i到节点i+1的距离;Si,i+1为前节点与下一节点的路径安全性程度;θ(i,i+1)为节点i和节点i+1之间的转向角度。
Si,i+1=
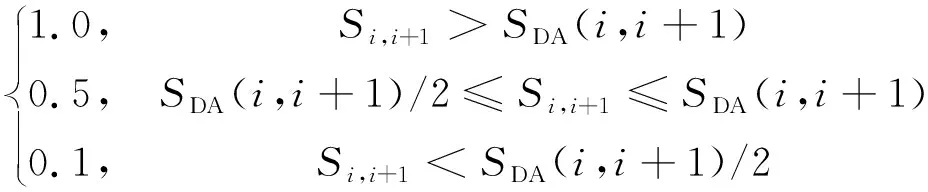
(7)
(8)
式中:SDA(i,i+1)为在路径点i和i+1之间的船舶安全会遇距离。
3 算法实现
3.1 静态路径规划算法的实现
本文提出的混合蚁群静态路径规划算法(hybrid ant colony static algorithm,HACSA)具体实施步骤如下。
1)步骤1,利用栅格法建立船舶航行环境模型,确定船舶起始点、目的地和碍航物位置。
2)步骤2,对混合蚁群算法中的参数设置初始值,比如,蚂蚁数量m,信息素挥发系数δ,初始信息素强度Q,引力势场系数Ka,人工势场影响系数R等。
3)步骤3,构建改进蚁群算法禁忌表并对其进行初始化设置。
4)步骤4,根据公式计算各路径点的信息素浓度。
5)步骤5,根据公式计算船舶所受合力的大小及方向,据公式计算当前位置的转移概率并确定下一步的移动位置j,并将该位置加入至禁忌表。
6)步骤6,更新完禁忌表后,判断蚂蚁是否到达目的地,若未抵达目的地则继续执行步骤5,反之,则记录该蚂蚁的路径长度和路径信息并进入到步骤7。
7)步骤7,令蚂蚁索引l=l+1,并判断l是否等于m,若不相等则返回步骤4,若相等则更新信息素浓度。船舶碰撞检测见图1。
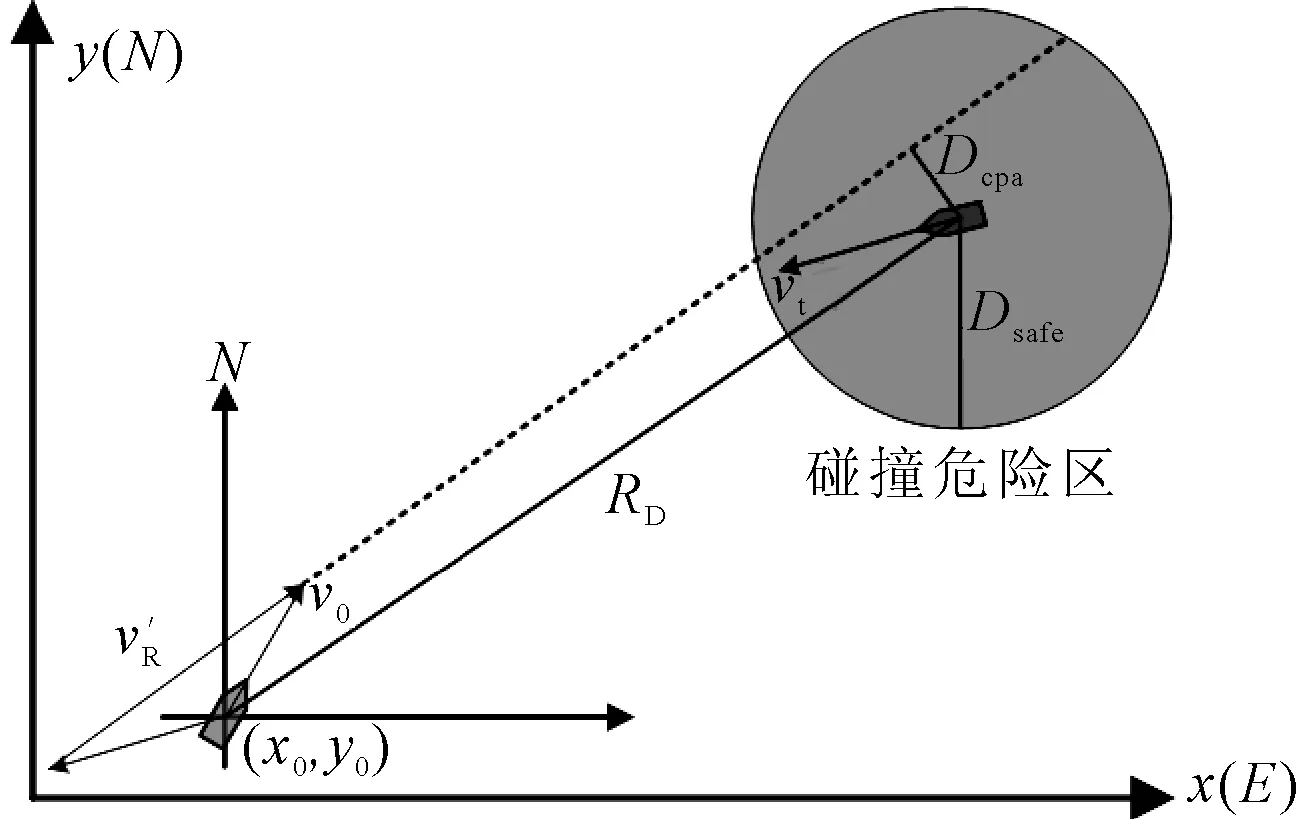
图1 船舶碰撞检测
3.2 动态路径规划算法的实现
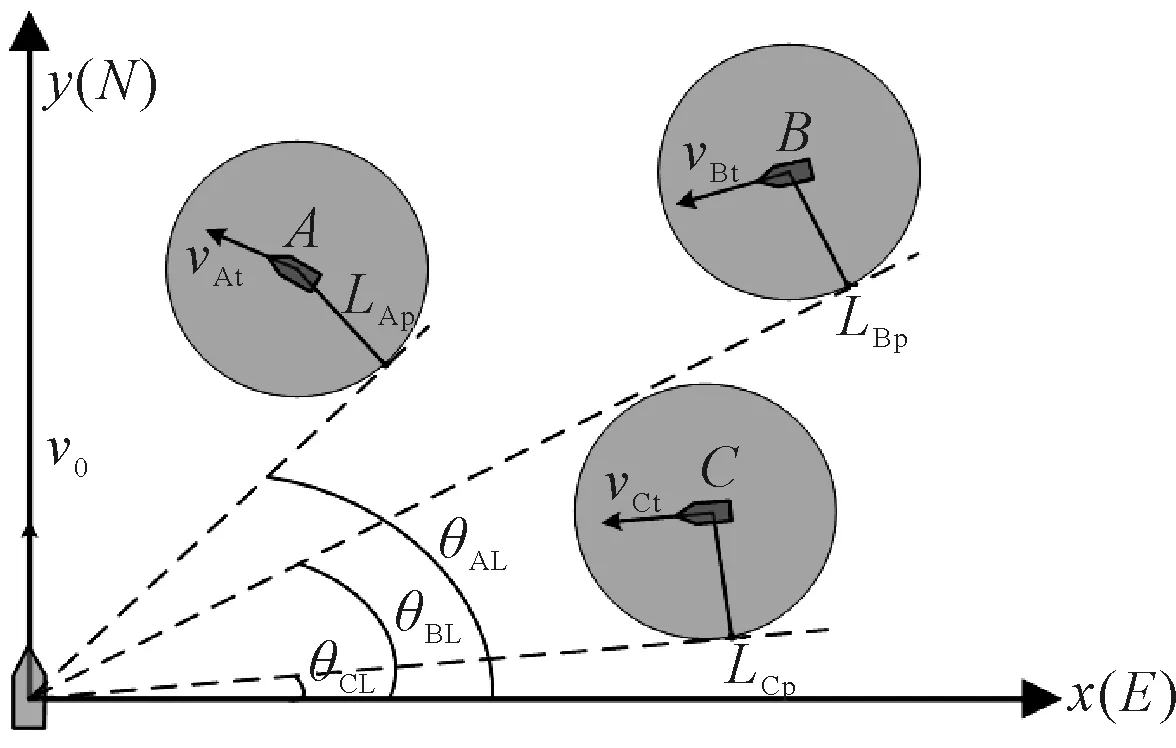
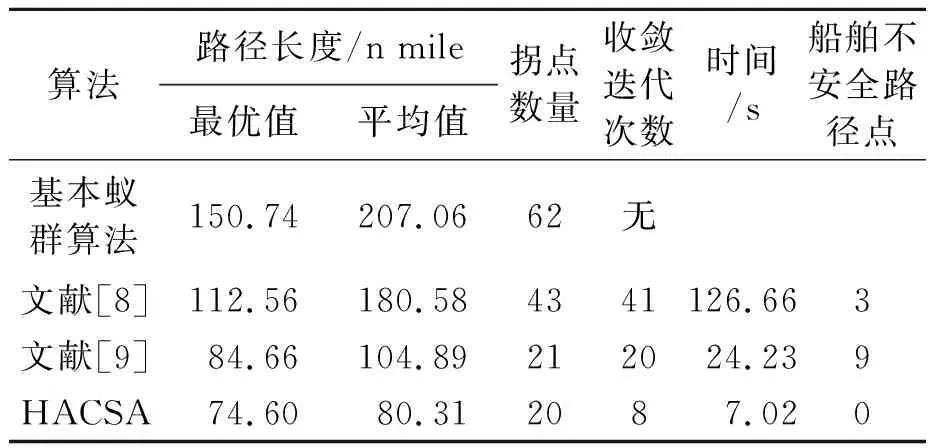
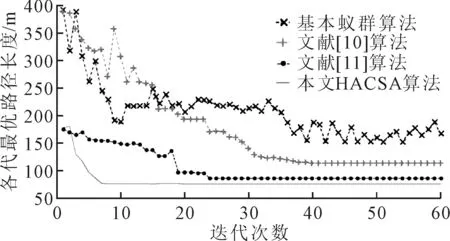
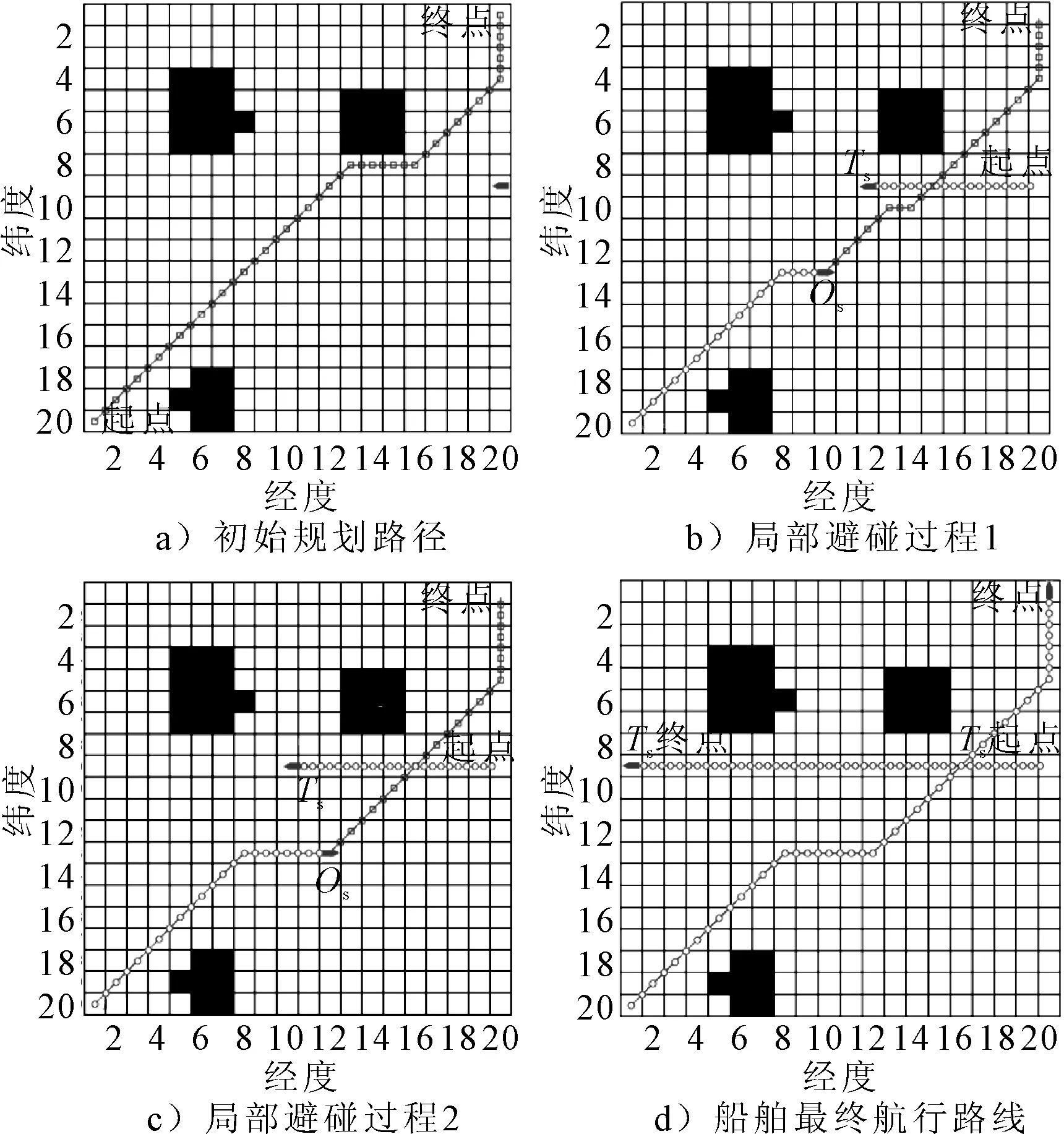
船舶动态路径规划算法在静态路径规划的基础上融入了碰撞危险计算、会遇态势识别和避碰行动采取。假设任意目标船与本船有个安全会遇半径Dsafe=SDA,若本船和目标船的船舶最近会遇距离Dcpa (9) 根据公式判断出本船与目标船之间的状态,如果有碰撞可能且具有避让责任时,本船应采取合适的避让措施。为简化运算,本文均采用右转向实现避让。在单船会遇情况下,已知本船与目标船的安全圆有2个切点,切点Rp(xRp,yRp)和切点Lp(xLp,yLp),见图2。 图2 船舶避让措施 本文将安全圆的左切点作为船舶避让导向点,左右切点按照式计算。 (10) (y-yt)(y-y0)=-(x-xt)(x-x0) (11) 式中:(x,y)为待求切点坐标;(x0,y0)为本船坐标;(xt,yt)为目标船坐标。 在多船会遇情况下,根据目标船个数分别计算出本船与目标船的左切点和右切点对应的角度。当前局面下存在3个目标船,见图3。 图3 多船避让措施 联立目标船安全圆公式和可求得本船与目标船的左右切点坐标,针对多目标船会遇局面,重复利用公式-计算出本船与各目标船的左切点角度分别为θAL、θBL、θCL。将选择目标船切点角度最小的左切点作为避让导向点,而切点角度θgoal的选择方法如式所示。 θgoal=min{θAL,θBL,θCL} (12) 基于上述分析,提出混合蚁群动态路径规划算法(hybrid ant colony dynamic algorithm,HACDA),算法具体实施步骤如下。 1)步骤1,采用HACSA规划出一条初始航行路径,船舶将沿初始路径航行。 2)步骤2,计算Tcpa、Dcpa和目标船相对运动方位θT。 3)步骤3,使用公式判断本船与目标船之间是否存在碰撞危险,若不存在,本船将沿初始路径继续航行;反之,则进入步骤5。 4)步骤4,依据θT值判断本船是否为让路船,若本船不是让路船,本船将沿初始路径继续航行,若本船为让路船,判断Dcpa≤Dsafe和Tcpa≤T是否同时成立。 5)步骤5,若Dcpa≤Dsafe和Tcpa≤T未同时成立,本船将沿初始路径继续航行。 6)步骤6,若Dcpa≤Dsafe和Tcpa≤T同时成立,则计算出本船与目标船的左切点角度θAL、θBL、θCL,利用公式求得θgoal,并在开始满足Dcpa≤Dsafe和Tcpa≤T时采取转向工作。 7)步骤7,本船转向避让后,实时重复步骤2~6判断本船是否应继续采取转向避让,直至本船到达目的地;若不需避让,则应用蚁群静态路径算法规划出从当前位置至目的地的航行路径,本船将沿新路径航行。 为验证HACSA在复杂航行环境中规划路径的稳定性,设定仿真环境为50×50(n mile),对比分析传统蚁群算法、文献[7]、文献[8]与HACSA的路径规划结果,见图4、5,表1。 表1 复杂环境下不同算法的仿真结果 由图4可知,除了传统蚁群算法,其他三种方法均可收敛得到各自的最优路径。在复杂环境下HACSA得到路径最短,距离为74.6 n mile。 图5中,HACSA的收敛速度最快。尽管船舶航行环境更复杂,HACSA仍在第8次迭代完成收敛,而文献[8]却在20次迭代以后才完成收敛,所以复杂环境几乎不会影响HACSA的运行效率。 图5 复杂环境下算法的迭代收敛 另外,文献[8]也加入了船舶安全性约束函数。由表1可知,相比于文献[8]中的方法,复杂环境几乎不会影响HACSA规划路径的安全性。所以无论是在复杂环境还是简单环境,HACSA均取得了相对最优的运行结果。 4.2.1 单目标船动态路径规划 为验证HACDA算法在静态障碍物和单一目标船环境下船舶动态路径规划的实用性,设计船舶航行区域为20×20(n mile),本船航行起点栅格序号为1,航行终点栅格序号为400。设定本船航向为45°、航速为20 kn,目标船的栅格起始序号为180、航向为180°、航速为16 kn。见图6。 图6 单目标船动态路径规划 由图6a)可知,在航行初始阶段,HACDA首先规划出一条自起点至终点的安全初始航行路径(避开静态和动态障碍物的初始位置),此后本船沿着初始路径航行。判断出两船之间存在碰撞危险,本船为让路船,且两船间的Dcpa和Tcpa值均小于规定值。避让过程中仍使用HACDA实时规划出自当前位置至目的地的局部新路径,见图6b)。一旦避碰过程结束,本船将沿局部新路径航行,若避碰过程未结束本船将继续进行避让。当本船航行到252号栅格时,本船与目标船的碰撞危险解除,见图6c)。此时本船将沿着更新后的局部新路径继续航行,最终抵达航行目的地。由图6(d)可知,在整个航行过程中,本船能识别动态障碍物并完成避让过程。 4.2.2 多目标船动态路径规划 为验证HACDA在静态障碍物和多运动目标船环境下船舶动态路径规划的稳定性,设计船舶航行区域大小为20×20(n mile),本船航行起点栅格序号为1,航行终点栅格序号为400,本船航向为45°、航速为20 kn;目标船1(TS1)起点栅格的序号为257、航向为180°、航速为16 kn;目标船2(TS2)起点栅格的序号为138,航向为225°,航速为10 kn;目标船3(TS3)起点栅格的序号为81,航向为315°,航速为10 kn。见图7。 图7 多目标船舶动态路径规划 首先采用HACDA规划一条初始路径,见图7a)。在图7b)中,当本船行驶至290号栅格时,可计算出本船与TS1的Dcpa值为0.94 n mile,θT值为18.65°,两船相距6.07 n mile,相对运动速度vR1为36 kn,Tcpa的值为10.4 min。由HACDA可判断出本船与TS1之间存在碰撞危险,且两船间的Dcpa和Tcpa值均小于约定值,本船右转实现以避让。 当本船行驶至274号栅格时,本船与TS1解除碰撞危险并将沿局部新路径向目的地航行,见图7b)。此时,由HACDA判断出本船与TS2之间存在碰撞危险,且两船间的Dcpa和Tcpa值均小于规定值,本船将采取右转向避让。随后本船与TS2结束对遇局面并将沿更新后的局部新路径驶向目的地,最终本船顺利抵达航行目的地。 为提高船舶路径规划的安全性与经济性,提出一种改进的蚁群算法用于船舶路径规划。针对蚁群算法迭代速度慢、易陷入局部最优等问题,通过在算法迭代初始阶段引入人工势场法,有效改善了算法的迭代速度和寻优能力。同时,为进一步使所规划路径符合实际情况,将路径长度、安全性、平滑性约束条件融入至信息素更新规则,并综合考虑航行规则约束。仿真实验证明,所提出算法的可行、有效。主要分析静态环境下的船舶路径规划,针对动态环境,仅实现了简单多船环境下船舶路径规划。然而,动态环境下的影响因素更多,如何实现更为复杂环境下的船舶动态路径规划是后续研究方向。
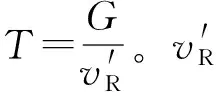

4 仿真实验
4.1 静态路径规划对比仿真实验
4.2 动态路径规划算法仿真实验

5 结论

