利用CND 法进行荔枝、龙眼叶片营养诊断研究的适宜性

朱永聪，罗东林，白翠华，姚丽贤

（华南农业大学资源环境学院，广东 广州 510642）

【研究意义】植物叶片营养诊断是进行作物养分管理的有力技术支持手段。对同种作物采用不同的叶片营养诊断方法进行诊断，结果往往不同，直接影响作物养分管理措施。因此，探究叶片营养诊断方法的优点和局限性，可为选择适用的诊断方法提供科学依据，提高诊断准确性。【前人研究进展】目前国际上采用的叶片营养诊断法主要有临界值法（Critical value approach，CVA）［1］、充足范围法（Sufficiency range approach，SRA）［2］、诊断施肥综合法（Diagnosis and recommendation integrated system，DRIS）［3］及引入干物质指数的M-DRIS 法［4-5］、组分营养诊断 法（Compositional nutrient diagnosis，CND）［6-8］、最优值百分比偏差法（Deviation from optimum percentage，DOP）［9-10］等。利用上述方法进行叶片营养诊断研究时，如何确定高产水平是关键。除CND 外，其他方法均由研究人员根据经验确定或利用生产中认可的高产水平进行诊断。如CVA 法通常将拟合模型最高理论产量的90%～95%水平作为高产值［11］。M-DRIS 法的高产水平来自作物前期调查数据，根据产量和品质确定高产群体和低产群体［12］。Walworth 等［4］提出利用养分元素的方差比例判别高产和低产群体，但未提出具体计算方式。CND 法首先建立产量与叶片每种养分累积方差比例函数关系模型，通过模型计算出每种养分的产量拐点值（Inflection point），保留作物实际产量范围内最高的拐点值作为高产临界值（Cutoff value），以此作为划分高产群体的依据［13］。CND 法被认为具有扎实数理统计基础、考虑养分间交互作用［14］，且注重样本产量代表性，及降低经验法人为因素干扰的优点［13,15］。CND 法已应用于马铃薯［7,15-16］、黄胡椒［17］、豇豆［18］、玉米［13,19-20］、枣［21］、葡萄［22］、芒果［23］、橙［24-25］和苹果［26］等诊断研究。【本研究切入点】本研究团队前期利用CND 法开展华南荔枝和龙眼叶片营养诊断研究，发现该法在确定荔枝、龙眼高产临界值时，存在养分拐点值往往超出实际产量范围、或为负数、或部分离散程度大的极值显著影响养分拐点值、或无法确定合适高产临界值等问题。然而，目前利用CND法建立叶片营养诊断指标的报道中，往往将CND法作为一种工具，忽略其在确定高产临界值时出现的问题，导致建立的诊断指标可能缺乏科学依据和实用价值。曾有少量研究对CND 法的养分产量拐点值模型拟合度提出质疑。如Hernández 等［24］指出，三阶多项式可能不是拟合叶片养分与产量关系的最好模型，而是提出一个sigmoid 模型（玻尔兹曼方程）代替三阶多项式的，并应用于香蕉［27］、橙［24］和仙桃仙人掌［28］的营养诊断。【拟解决的关键问题】本研究利用CND 法拟合荔枝、龙眼各种养分含量累积方差函数-产量模型，分析产量模型中异常值产生原因及对产量模型影响，考察养分拐点值随产量模型的变化及对高产临界值选取的影响，探讨高产群体的代表性和实用性，总结CND 法划分荔枝、龙眼高产水平的不足，明确该法在多年生大型木本果树叶片营养诊断研究的局限性。

1 材料与方法

1.1 试验地概况

2016—2017 年选择22 个（广东7 个、广西7 个、海南6 个、云南1 个、福建1 个）管理相对较好的成年妃子笑荔枝果园，果园地理坐标为19°21′～25°19′N、109°32′～117°27′E。每个果园选择约10 株树体大小接近、树冠相对独立完整的试验树，共193 株。试验地树龄为10～20 年，种植密度270～630 株/hm2。

2017—2019 年选择管理相对较好的8 个（广东茂名5 个、广西北海2 个、玉林1 个）储良龙眼园，果园地理坐标为21°35′～22°15N′、109°13′～110°57′E。每个果园选择约10 株树体大小接近、树冠相对独立完整的试验树，共82株。试验树树龄20～25 年，种植密度为75～270株/hm2。

1.2 叶片样本采集及果实产量记录

于2016 年妃子笑果实膨大期（4 月中旬到5月中旬）、末次梢老熟期（10 月中旬到11 月下旬）和2017 年妃子笑果实膨大期（4 月下旬到5月下旬）采集荔枝叶片样本。于2017 年龙眼末次梢老熟期（2017 年12 月中旬至2018 年1 月上旬）和2018 年果实膨大期（5 月中旬至6 月上旬）、2018 年龙眼末次梢老熟期（2018 年12 月中旬至2019 年1 月上旬）和2019 年果实膨大期（5 月中旬至6 月中旬）采集龙眼叶片样本。叶片样本具体采集方法见前期研究［29-30］。由于气候对荔枝、龙眼成花坐果影响大，导致不同年份间可采样及正常挂果的试验树数量变化较大。因此，荔枝在2016 年以193 株片样本养分含量与产量数据、2017 年以159 株的数据进行叶片营养诊断研究。龙眼在2017—2018 年以82 株树、2018—2019 年以52 株树进行研究。

1.3 叶片样本处理与测试

叶片样本经洗涤、烘干、制样后，部分样本用H2SO4-H2O2消解，采用凯氏定氮仪测定N 含量；部分用HNO3-HClO4消解，采用ICP-OES（710-ES，VARIAN，USA）法测定P、K、Ca、Mg、S、Fe、Mn、Cu、Zn、B 含量。用标准物质（GBW07603和GSV-2）控制测试质量。

1.4 计算荔枝、龙眼高产临界值

参考Parent 等［13］方法，计算荔枝、龙眼高产拐点值。

式中，R为引入值；N、P、K…为养分元素，是叶片中养分元素含量的百分数；Vx为观测群体的分析参数；d为诊断元素个数；n为所有果树株数；n1为每次循环中产量最高的株数；n2为每次循环中剩余株数；n=n1+n2；S2Vxn1为n1的参数Vx的方差；S2Vxn2为n2的参数Vx的方差；在第一次循环计算中，n1取2 株，n2=n-n1；以后每次循环中n1增加1 株，n2相应减少1 株，直到最后剩下2 个最低产的果树组成n2，但始终保持n=n1+n2；FCi（Vx）为分析参数；方程（5）中分子表示n1-1 个分析参数fi（Vx）之和，分母表示所有分析参数fi（Vx）之和；方程（6）为各养分累积方差函数参数FCi（Vx）与产量（Y）之间关系；对方程（6）2 次求导得到方程（7）。

1.5 数据处理与统计

试验数据利用Excel 2011 整理，制作养分累积方差比例函数与产量的散点图，并模拟方程，用SPSS 检验方程拟合度的显著性。

2 结果与分析

荔枝、龙眼不同年份果实产量及不同生育期叶片养分含量情况见本团队前期研究［28-29］。

2.1 荔枝、龙眼叶片养分含量累积方差比例函数与果实产量关系模型中的异常值

由于同一果园不同试验果树的株产差异较大［29-30］，本研究将每株试验果树作为独立的采样单元，以单株株产乘以种植密度的方式计算产量，并拟合荔枝、龙眼产量与不同生育期叶片养分含量累积方差比例函数（以下简称比例函数）的关系模型（图1～图7）。本文仅展示出现异常点的图。

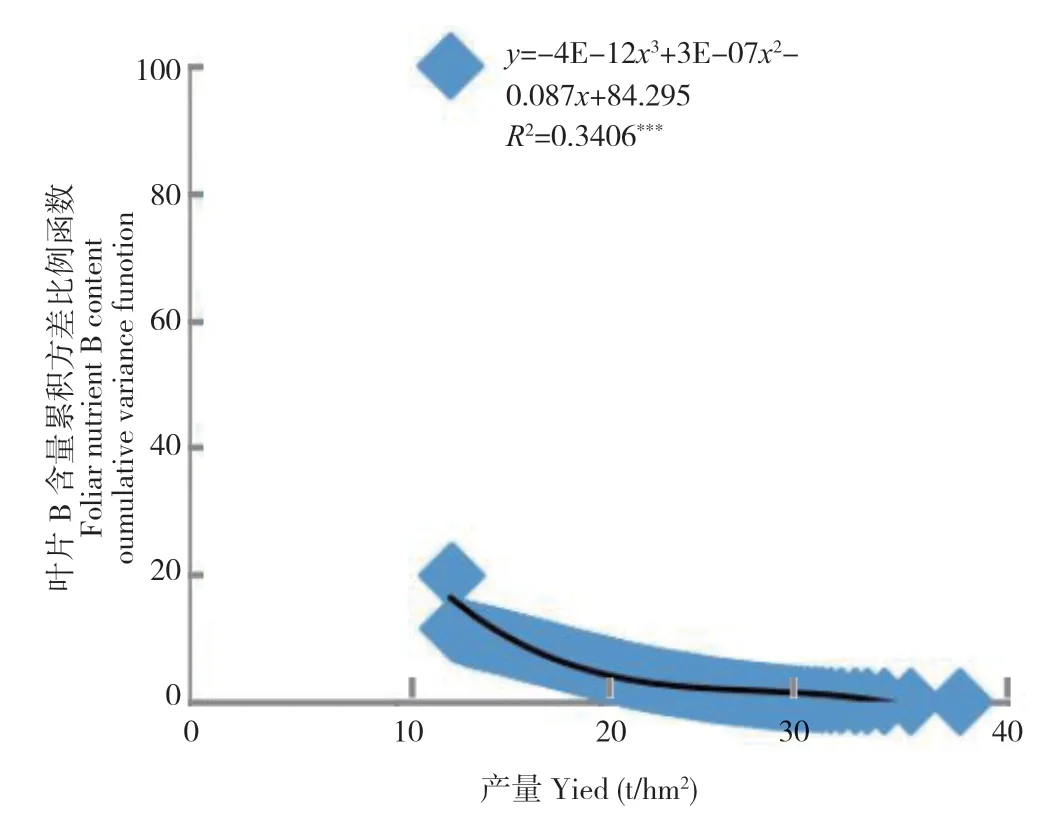
图1 2016 年荔枝果实膨大期叶片养分含量累积方差比例函数与2016 年产量之间的关系（n=193）Fig.1 Relation between the cumulative variance function of foliar nutrient in litchi at FSS of 2016 and fruit yield of 2016 (n=193)

从图1～图7 可以看出，荔枝、龙眼果实产量与不同生育期叶片养分含量比例函数的关系模型中，均出现某些叶片养分含量比例函数的极端值对模型影响显著的现象。如图1 叶片的B 含量，图2 叶片的P 和Ca 含量，图3 的叶片P 和Zn 含量，图4 叶片的K、Ca、S、Fe 和Mn 含量，图5叶片的P、Ca、Mg、Zn 和B 含量，图6 叶片的N、P、K、Ca、S、Fe、Mn、Zn 和B 含量及图7 的几乎所有叶片养分含量的比例函数均出现明显偏离绝大部分比例函数值的异常高值或低值。

本研究将叶片养分含量比例函数与总体函数偏差大的函数分为两种类型。一种为出现异常高值。如图1 叶片的B 含量，图2 叶片的P 含量，图3 叶片的P 含量，图4 叶片的K、Fe 和Mn 含量，图5 叶片的P、Ca、Zn 和B 含量，图6 叶片的P、K、Ca 和Fe 含量和图7 叶片的K、Ca、Mn、Cu 含量的比例函数；另一种为出现异常低值。如图2 叶片的Ca 含量，图3 叶片的Zn 含量，图4 叶片的Ca 和S 含量，图5 叶片的Mg 含量，图6 叶片的N、S、Mn、Zn 和B 含量和图7 叶片的N、P、Mg、S、Fe 和B 含量的比例函数。

图2 2016 年荔枝末次梢老熟期叶片养分含量累积方差比例函数与2017 年产量之间的关系（n=159）Fig.2 Relation between the cumulative variance function of foliar nutrient in litchi at TSMS of 2016 and fruit yield of 2017 (n=159)

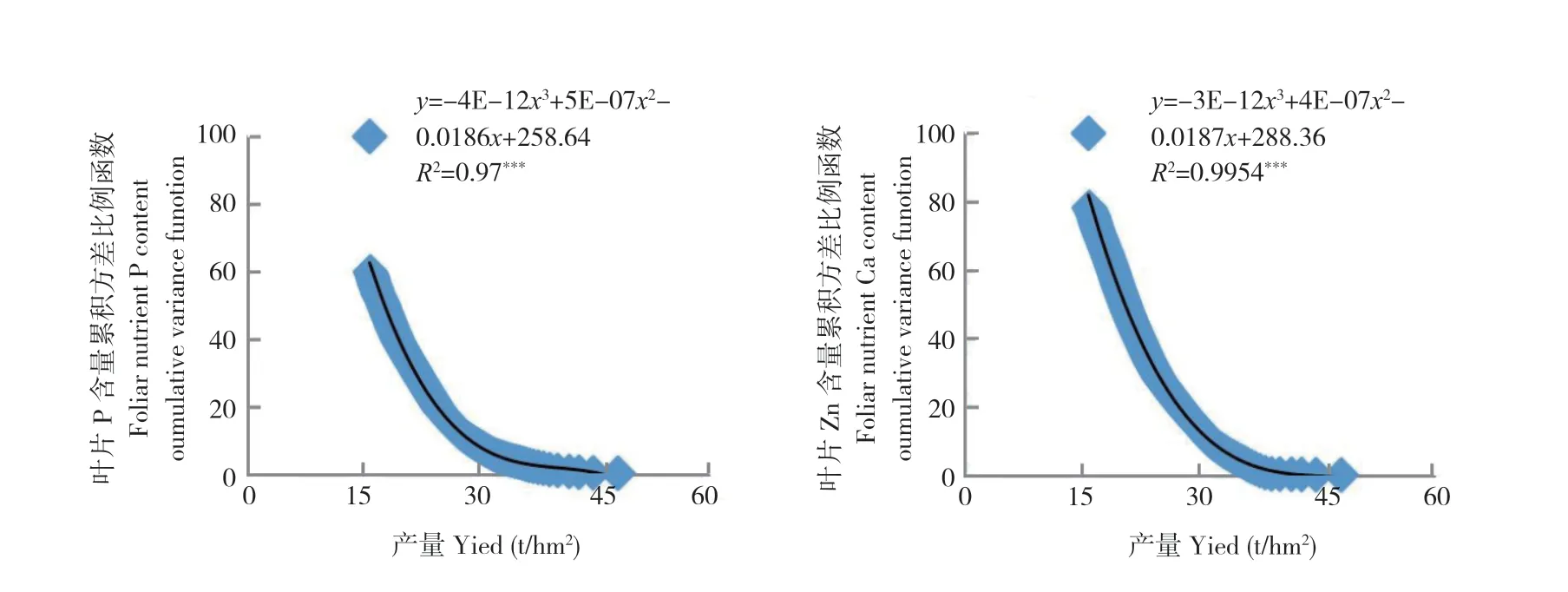
图3 2017 年荔枝果实膨大期叶片养分含量累积方差比例函数与2017 年产量之间的关系（n=159）Fig.3 Relation between the cumulative variance function of foliar nutrient in litchi at FSS of 2017 and fruit yield of 2017 (n=159)

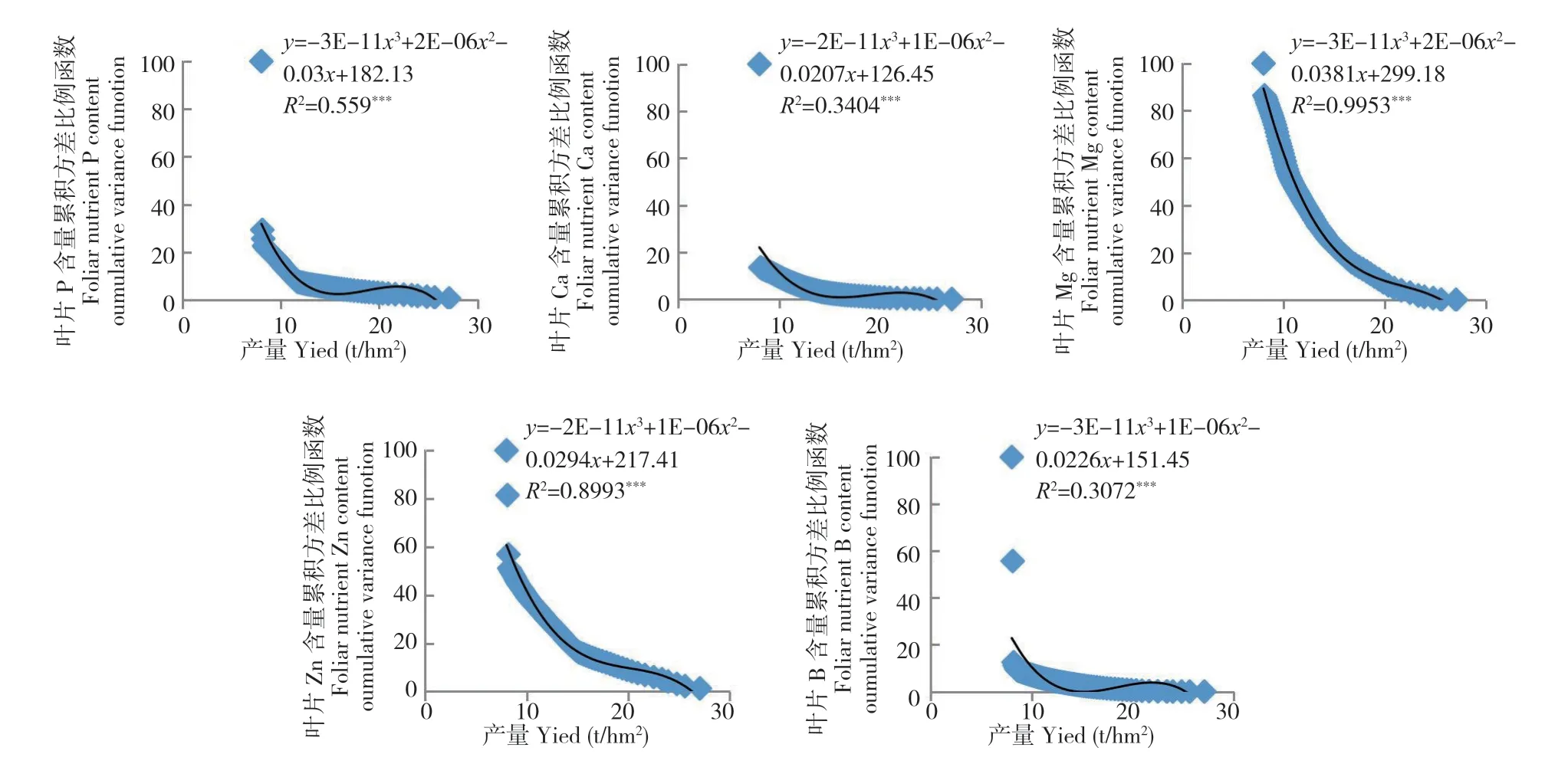
图5 2018 年龙眼果实膨大期叶片养分含量累积方差比例函数与2018 年产量之间的关系（n=82）Fig.5 Relation between the cumulative variance function of foliar nutrient in longan at FSS of 2018 and fruit yield of 2018 (n=82)

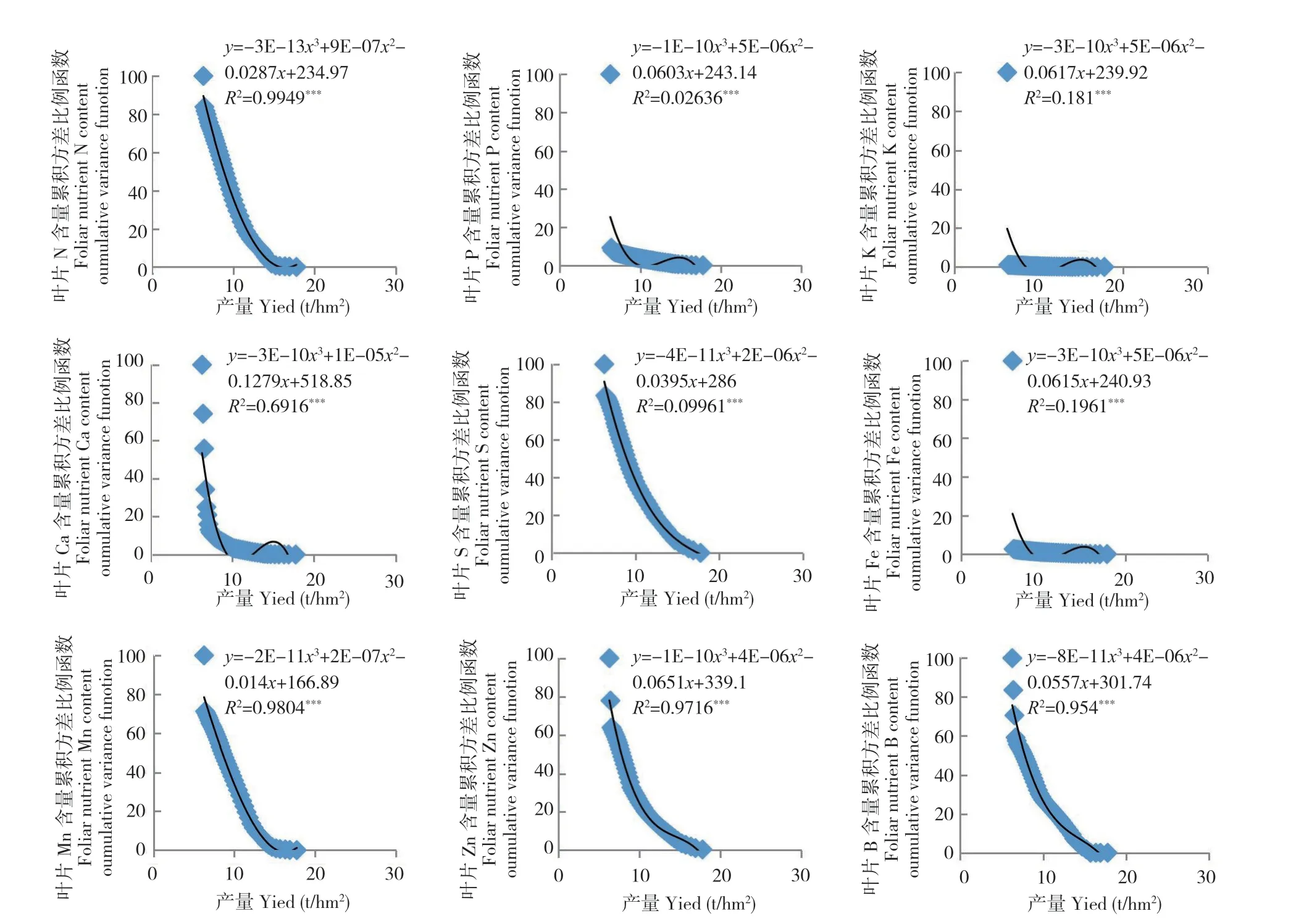
图6 2018 年龙眼末次梢老熟期叶片养分含量累积方差比例函数与2019 年产量之间的关系（n=49）Fig.6 Relation between the cumulative variance function of foliar nutrient in longan at TSMS of 2017 and fruit yield of 2018 (n=49)

在计算荔枝龙眼叶片养分含量比例函数参数时发现，当从最低产样本开始计算时，如果不同样本差异大，将导致分析参数Vxn的方差S2Vxn的变化也较大。若从最低产样本算起的第n个（n≥2）与第n+1 个分析参数方差S2Vxn2（n2≥2）的差异过大时，如在荔枝的变异系数为72.7%～112.2%及龙眼的变异系数为45.6%～ 138.0%，会出现图1～图7 中部分叶片养分含量比例函数的数值明显高于或偏离绝大部分函数值的现象。由于方差S2Vxn1（n1=n-n2，n2≥2）和S2Vxn1-1是由所有样本观测值计算所得，数值变化不大，故分析参数fi（Vx）=S2Vxn1/S2Vxn2（n1=n-n2,n2≥2）和fi-1（Vx）=S2Vxn1-1/S2Vxn2+1之间的差异主要取决于S2Vxn2（n2≥2）和S2Vxn2+1之间的差异。本研究中，正常情况下荔枝分析参数fi=n-3(Vx)（i=1，2，3……n-3）和fi-1=n-4(Vx)的差值在0.4～4.4，龙眼的差值为0.7～ 8.9。出现异常高值的荔枝分析参数差值可达到40.1～ 80.1，为正常情况下的10 倍以上，而龙眼的差值为18.5～98.8，为正常情况下的数倍以上。存在异常低值的龙眼分析参数差值为8.8～ 28.8。上述分析参数的较大差异，导致FCi(Vx)出现异常值，从而明显降低FCi（Vx）=AY3+BY2+CY+D 的拟合度。表明在养分累积方差函数FCi(Vx)与产量关系模型中，当y轴上的值接近100%时，即使拟合显著，个别异常值对模型的影响较大。

2.2 异常值对荔枝龙眼叶片养分含量产量拐点值的影响

根据图1～图7 的拟合模型，计算获得荔枝、龙眼不同生育期叶片不同养分对应的产量拐点值（表1）。将各图中出现的极值剔除后，重新拟合模型（具体模型略）计算获得的拐点值，见表1 括号内数值。

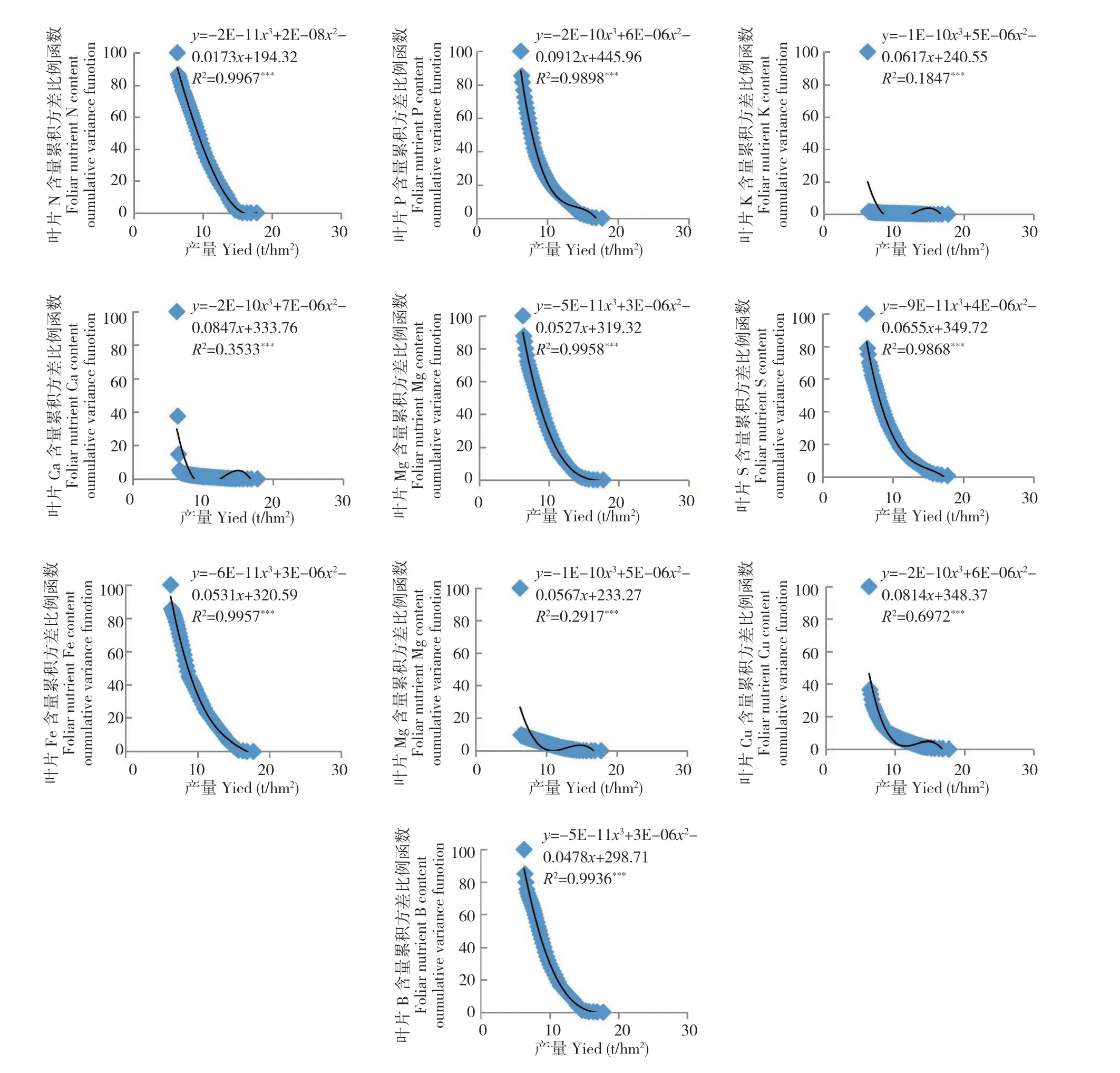
图7 2019 年龙眼果实膨大期叶片养分含量累积方差比例函数与2019 年产量之间的关系（n=49）Fig.7 Relation between the cumulative variance function of foliar nutrient in longan at FSS of 2019 and fruit yield of 2019 (n=49)

由表1 可知，发现剔除极值后，根据重新拟合的关系模型计算获得的拐点值，与原拐点值相比，存在3 种情况：（1）前后拐点值相同。如2016 荔枝末次梢老熟期叶片的Ca 含量，2018 年龙眼末次梢老熟期叶片的P、K、S 和Fe 含量的拐点值等；（2）前后拐点值接近。如2016 年荔枝果实膨大期叶片的B 含量，2019 年果实膨大期叶片的P、K、S、Fe 和Cu 含量的拐点值等；（3）前后拐点值差异显著。如2017 年荔枝果实膨大期叶片的Zn 含量，2017 年龙眼末次梢老熟期叶片的K、Ca 和Fe 含量，2019 年龙眼果实膨大期叶片的N、Ca、Mg、Mn 和Zn 含量的拐点值等。表明剔除极值对理论高产水平计算结果有不同影响，但影响缺乏规律性。此外，在剔除极值前后，样本量和计数量纲也随之发生改变，表明CND 法应用Cate-Nelson 循环计算养分拐点值时也会受到样本量和计数量纲的限制。

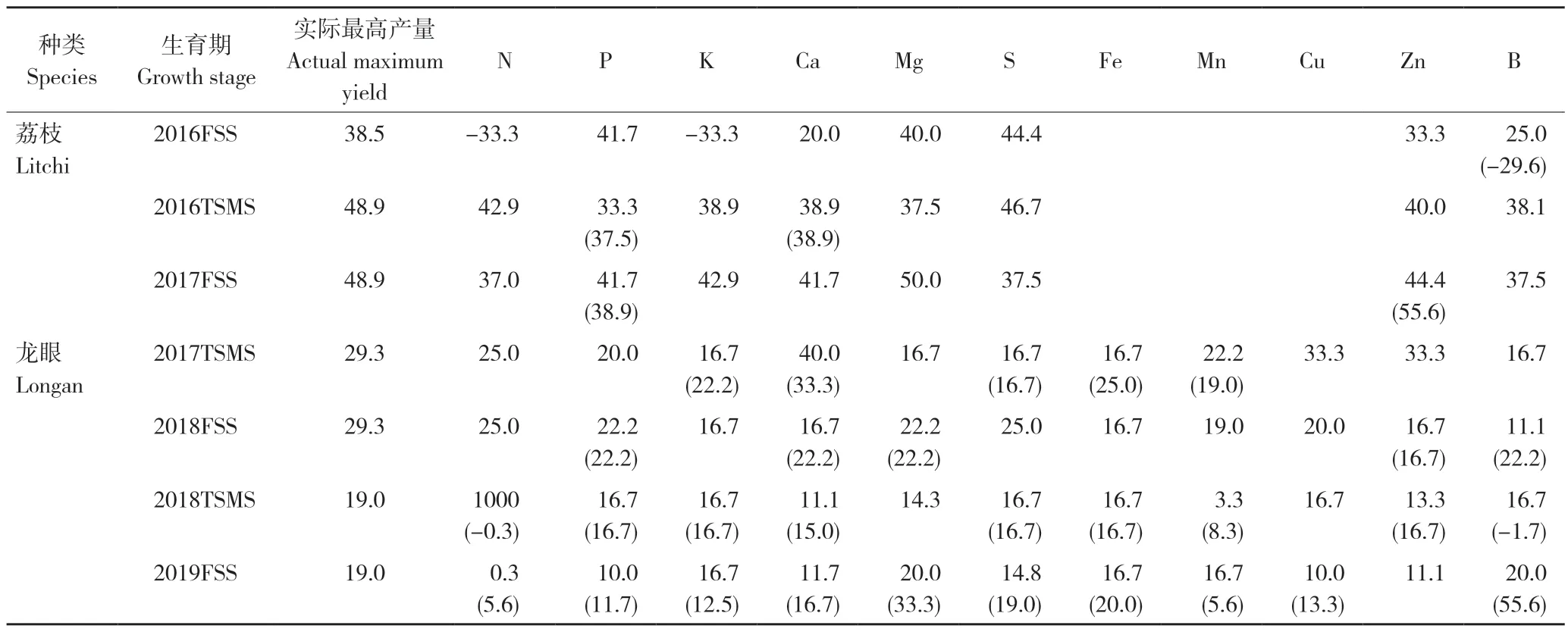
表1 2016—2019 年荔枝、龙眼不同生育期叶片养分的产量拐点值（t/hm2）Table 1 Inflection points of fruit yield for foliar nutrients of litchi and longan at different growth stages during 2016-2019 (t/hm2)

此外，剔除极值前后获得的高产拐点值与荔枝龙眼实际最高产量进行比较，存在3 种情况：（1）剔除极值前后的拐点值均超出实际最高产量。如2016 年荔枝果实膨大期P、Mg 和S 含量的拐点值等；（2）剔除极值后的拐点值超出实际最高产量。如2017 年荔枝果实膨大期Mg 和Zn 含量的拐点值与2019 年龙眼果实膨大期Fe 含量的拐点值等；（3）剔除极值前后的拐点值均在实际产量范围内。表明是否剔除极值对某些元素的拐点值是否高于实际最高产量、进而成为备选高产临界值没有明确一致的影响。

2.3 荔枝、龙眼高产临界值的确定

目前，在划分作物高产群体时，国际上往往将低于实际最高产量的最高拐点值［13,18］、最低拐点值［31］或各养分拐点值的平均值［21,32］作为作物高产临界值选择标准。在多数研究中，一般选择低于实际最高产量的最高拐点值作为高产临界值。有研究将低于实际最高产量且高产群体比例≥12%的最高拐点值作为高产临界值［25-26］，但这种指定高产群体比例的作法缺乏数理依据。按照上述研究［13,18］，仅说明应选择低于实际最高产量的最高拐点值作为高产临界值。国外研究在应用CND 法划分作物高产群体时，高产群体一般占总体样本的10%～40%［24,33］。本研究将低于实际最高产量且高产群体比例为10%～40%的拐点值作为荔枝龙眼选择高产临界值的原则，获得荔枝、龙眼3 类高产临界值及其高产群体（表2）。

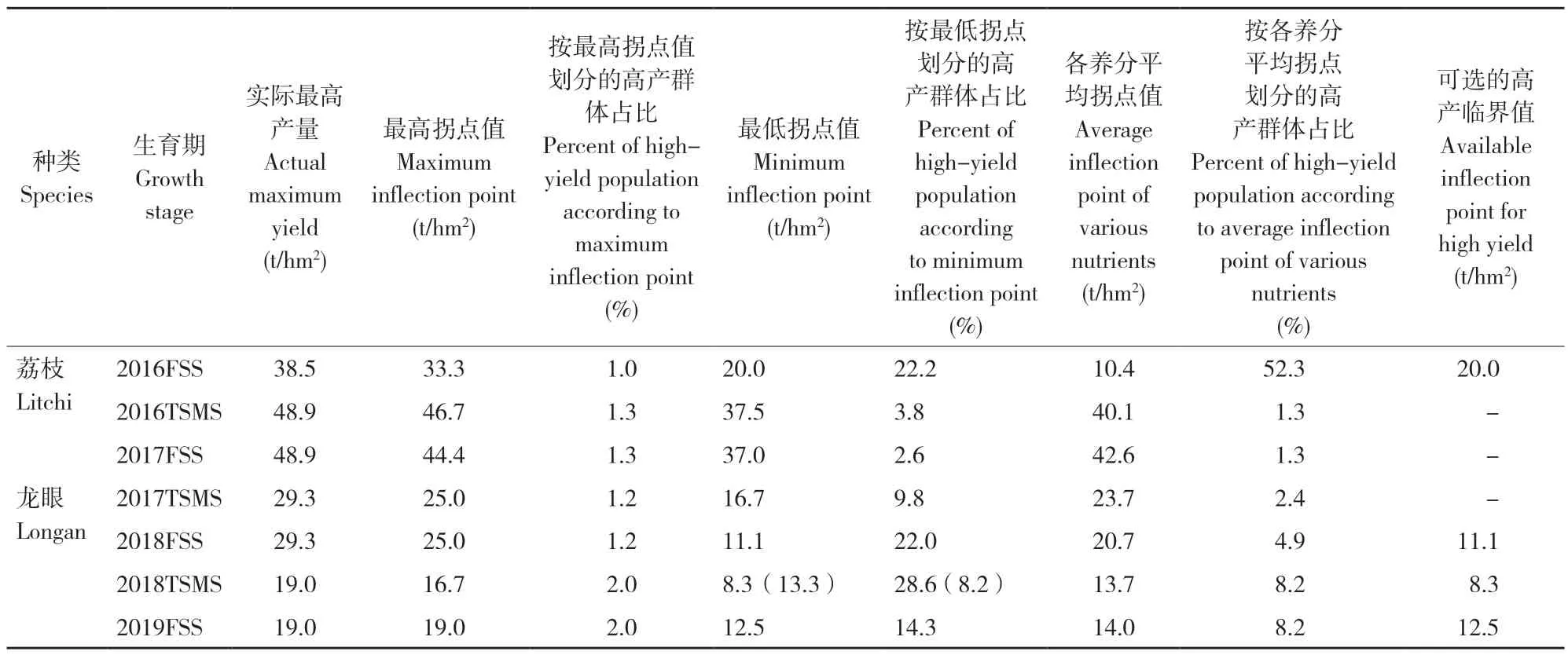
表2 2016—2019 年荔枝、龙眼不同生育期高产临界值情况Table 2 Cutoff values of high yield for litchi and longan at different growth stages during 2016-2019

如选择低于实际最高产量的最高拐点值作为高产临界值，两种果树不同年份不同生育期的高产群体仅占1.0%～2.0%，实际可用样本量不超过两个，诊断结果缺乏代表性。考虑到高产群体的样本量，部分研究者选择实际产量范围内的最低养分拐点值划分高产群体［31］。荔枝2016 年末次梢老熟期、2017 年果实膨大期和龙眼2017 年末次梢老熟期3 个时期备选的高产临界值即使选择最低的产量拐点值，高产群体仅分别占3.8%（4个）、2.6%（4 个）和9.8%（7 个），也存在样本量太少、结果缺乏代表性的问题。龙眼2018 年末次梢老熟期如选用最低的拐点值（8.3 t/hm2）作为临界值，则高产群体占28.6%，但此高产水平远低于生产中认可的高产水平（至少为15 t/hm2以上），严重低估龙眼的产量潜力，诊断结果缺乏实际指导意义。如选用次低的拐点值（13.3 t/hm2）作为临界值，则高产群体仅占8.2%，数量不足。同样问题也出现在龙眼2018、2019 年的果实膨大期。

为避免这种问题，研究人员将各养分平均拐点值作为高产临界值。如Labaied 等［21］将枣树叶片11 种养分拐点值的均值作为高产临界值。在本研究中，如选择各养分拐点值的均值作为高产临界值，除荔枝2016 年果实膨大期外，荔枝、龙眼两年不同生育期的高产群体占总体样本的1.2%～8.2%，样本量仅为1～4 个，仍然出现样本量太少、结果缺乏代表性的现象。

此外，荔枝2016 年果实膨大期如选用各养分拐点值的平均值（10.4 t/hm2）作为高产临界值，则高产群体占52.3%，但此临界值也明显低于生产中认为的高产水平（15 t/hm2以上）。仅选用2016 年荔枝果实膨大期的最低拐点值（20.0 t/hm2）作为临界值时，才与生产上认为的高产水平较为接近且高产样本数量适合（表2）。

对于荔枝、龙眼可选的高产临界值，荔枝仅有2016 年果实膨大期的高产临界值可选；龙眼2017 年末次梢老熟期缺乏可选的高产临界值；龙眼2018 年果实膨大期、2018 年末次梢老熟期和2019 年果实膨大期可选的高产临界值也均明显低于生产中认可的高产水平。以上结果表明，利用CND 法确定的龙眼高产水平，存在忽视龙眼产量潜力的问题。

3 讨论

在国际上研究人员利用CND 法确定高产临界值时，常出现拐点值异常的情况［18-19，24，26，28，32］（表3）。本研究中荔枝、龙眼某些拐点值也出现异常。拐点值异常体现为：拐点值超出实际产量范围、接近实际产量的最低产量，甚至拐点值为负值。

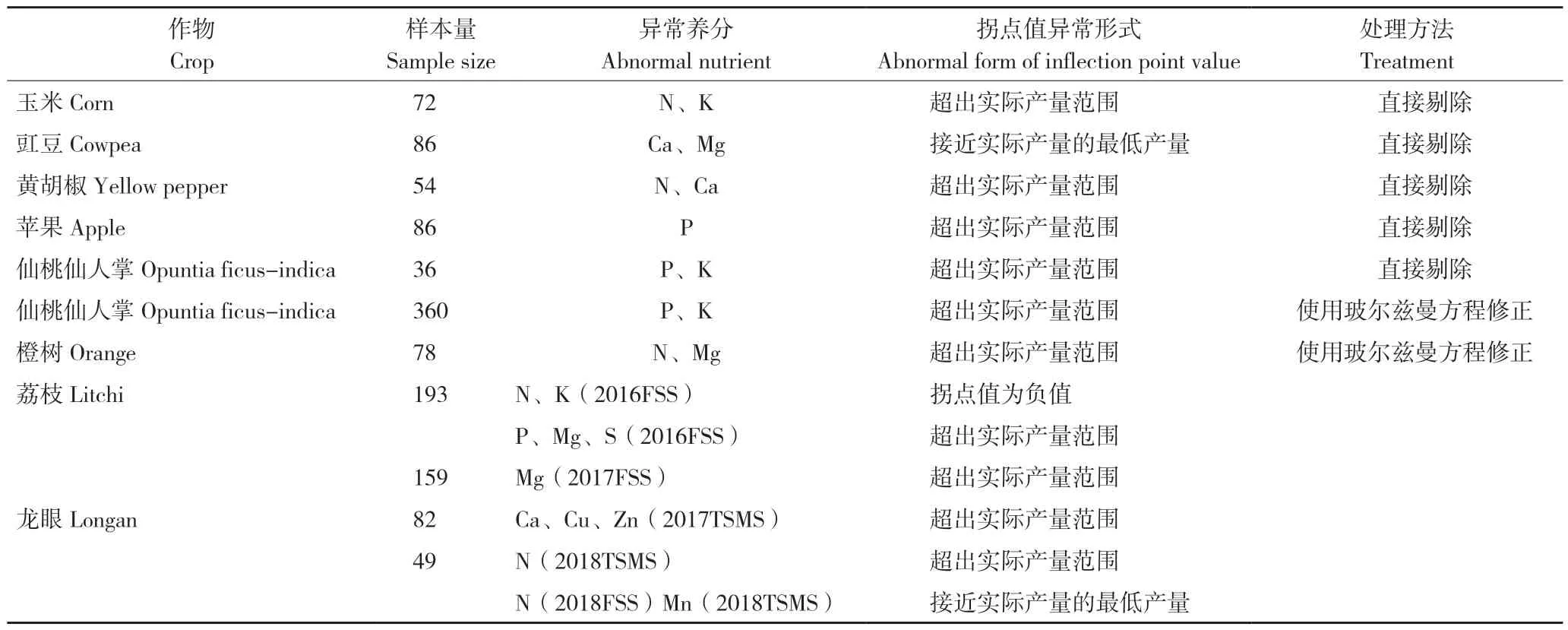
表3 不同作物的异常拐点值及处理方法Table 3 Abnormal inflection point values in different crops and corresponding treatments

当某养分拐点值出现上述3 种情况，研究人员一般直接将其剔除。这不仅导致计算效率降低，还忽略拐点值异常的成因，而这些被剔除的拐点值可能在修正后被确定为高产临界值。这是由于拐点值受模型拟合程度影响大，使用拟合度更佳的玻尔兹曼方程作为替代模型，对养分拐点值进行修正，可能会使异常拐点值成为高产临界值备选值之一［24,28］。但采用玻尔兹曼方程修正养分拐点值时，也可能出现偏离实际产量的问题。如Hernández 等［24］划分78 株橙树（93.25～196.65 kg/株）的高产群体时，使用CND 法三次多项式方程计算获得的高产拐点值为164.95～280.17 kg/株，应用玻尔兹曼方程获得的为34.57～114.10 kg/株，两种方法计算结果差异显著。

若将低于实际最高产量的最高拐点值作为高产临界值，则使用三次多项式方程获得的高产临界值接近实际产量的最高值，而应用玻尔兹曼方程获得的高产水平接近实际产量的最低值。因此，在多年生木本果树上应用玻尔兹曼方程虽可使模型拟合度更优，但高产临界值可能明显下降，甚至与生产上的低产水平相当，这意味着用玻尔兹曼方程代替三次多项式方程未必适合。不同作物利用不同方程计算获得的高产临界值差异明显，意味着不同作物需用不同的方程，如样本个体差异大的果树更适宜应用三次多项式方程，而玻尔兹曼方程可能更适于样本差异不大的大田作物。然而，目前国际上此类研究主要为评估不同方程对同一作物拟合模型的适宜性，缺乏不同方程对不同类型作物适宜性的评估，故可能出现玻尔兹曼方程适用于香蕉［27］和仙桃仙人掌［28］，但应用在橙树［24］上并不优于三次多项式方程的情况。因此，未来仍需更优的方程用于拟合产量与养分含量累积方差比例函数，并进行评估不同方程对不同类型作物拟合模型的适宜性。

若采用最低拐点值划分高产群体，负的拐点值应剔除。同时，最低拐点值接近实际产量的最低产量，划分的高产群体虽样本量大，但明显低于实际生产水平。然而，即使剔除该异常拐点值，次低拐点值划分的高产群体仍面临样本量大却缺乏实际指导意义或样本量太少而缺乏代表性等问题。

若将各养分拐点值的平均值作为作物高产临界值，则上述拐点值的3 种异常情况均会显著影响其平均值，进而影响高产群体的划分。如在荔枝2016 年果实膨大期，最高拐点值为44.4 t/hm2，最低正拐点值为20.0 t/hm2，由于存在负拐点值，平均拐点值仅为10.4 t/hm2，明显低于荔枝生产中认为的高产水平15 t/hm2。在仙桃仙人掌研究中，Magallanes 等［32］考虑到P 和K 对应的拐点值超出实际产量范围，认为有效平均拐点值的计算不能包括P 和K。因此，在出现异常拐点值的情况下，计算各养分拐点值平均值时不能兼顾养分间的平衡。

通过以上分析，结合荔枝龙眼叶片养分含量的状况［29-30,34-35］，我们认为，研究样本量、计数量纲和作物叶片养分含量状况均可能影响养分拐点值。目前国际上尚没有广泛认可的异常拐点值的处理方法，不同研究人员的处理方法不一，主观性较强，影响对高产临界值的选择。同时，国际上也缺乏严谨的高产临界值选定原则，确定高产临界值也存在较强主观性。若选择低于实际最高产量的最高拐点值作为高产临界值，则缺乏考虑不同养分对产量的贡献不同，与CND 法考虑养分交互作用的优点相驳。然而，将各养分拐点值平均值作为高产临界值，虽然平均值看似是综合考虑所有养分，但仍然缺乏理论依据。另外，利用最低拐点值划分高产群体，虽高产群体样本量大，但往往因忽略作物产量潜力而缺乏实际生产应用价值。这说明，CND 法划分高产水平存在较强的主观因素，并不优于依靠经验划分高产群体。

与产量较为稳定的小型木本果树（如柑橘和葡萄等）相比，荔枝、龙眼产量波动很大。本研究中用于试验的荔枝、龙眼果树个体产量及年际产量变异大，尤其是在接近最低和最高产量时，样本密度变得很低。若选择低于实际最高产量的最高拐点值作为高产临界值，会出现荔枝、龙眼高产临界值接近实际最高产量，但高产群体样本量太少、结果缺乏代表性的现象。

另外，根据上述3 种原则确定的荔枝、龙眼高产临界值，也存在年份间的明显差异。表明利用CND 法获得的高产水平年际稳定性差，用当年获得的高产水平对荔枝、龙眼叶片营养状况进行诊断，诊断结果并不能应用于第二年的生产指导，诊断研究的意义有限。因此，CND 法在产量波动大的多年生大型木本果树上的应用具有较大局限性。

4 结论

本研究进行荔枝、龙眼叶片营养诊断时，应用CND 法计算两种果树不同年份不同生育期各养分拐点值，并进一步确定，利用高产临界值来划分高产群体的过程中，对养分拐点值异常值的处理和高产临界值的取舍均存在较大主观性。研究的样本量、计数量纲和作物叶片养分含量状况均可能影响养分拐点值，导致产生异常值。根据不同高产临界值选定原则确定荔枝、龙眼高产临界值时，均可能出现因高产群体样本量不足而缺乏代表性，或高产临界值明显低于实际生产的高产水平而缺乏实际生产应用价值等问题，具有较大局限性。另外，CND 法获得的荔枝、龙眼年际间高产水平差异大、稳定性差，当年营养诊断结果难以用于指导翌年荔枝龙眼生产。建议在产量波动大的多年生木本果树上谨慎应用CND 法进行叶片营养诊断。