随机变量及其分布单元测试卷(A 卷)
■河南省濮阳市第一高级中学 梁文强
■河南省濮阳市教育局 张献伟
一、选择题(本题共12 小题,每小题5分,共60分,在每小题给出的四个选项中只有一项是符合题目要求的。)
1.从只有2张有奖的8张彩票中不放回地随机逐张抽取,设X表示直到抽到中奖彩票时的次数,则P(X=3)=( )。
2.已知随机变量X的分布列如表1,若E(X)=1,D(2X-1)=2,则m=( )。

表1
3.现有语文、数学课本共7本(其中语文课本不少于2本),从中任取2本,至多有1本语文课本的概率为,则语文课本有( )。
A.2本 B.3本
C.4本 D.5本
4.某水稻种植研究所调查某地水稻的株高,发现株高(单位:cm)服从正态分布,其密度函数为(-∞,+∞),则下列说法正确的是( )。
A.该地水稻株高在120 cm 以上的数量和株高在80 cm 以下的数量一样多
B.该地水稻的平均株高为200 cm
C.随机测量一株水稻,其株高在区间(80,90)和在区间(100,110)的概率一样大
D.该地水稻株高的方差为10
5.某企业生产的12个产品中有10个一等品,2个二等品,现从这批产品中任意取4个,则其中恰好有1 个二等品的概率为( )。
6.已知随机变量ξ和η满足2ξ+η=8,若ξ~B(10,0.4),则E(η),D(η)分别是( )。
A.0和9.6 B.4和2.4
C.0和2.4 D.4和9.6
7.将3颗骰子各掷一次,记事件A表示“三个点数都不同”,事件B表示“至少出现一个1点”,则条件概率P(B|A)为( )。
8.有甲、乙、丙三个工厂生产同一个型号的产品,甲厂生产的次品率为10%,乙厂生产的次品率为20%,丙厂生产的次品率为30%,生产出来的产品混放在一起,已知甲、乙、丙三个工厂生产的产品数分别占总数的50%、30%、20%,任取一件产品,则取得的产品为次品的概率是( )。
A.0.83 B.0.79
C.0.21 D.0.17
9.将一枚质地均匀的硬币重复抛掷10次,则正面朝上出现的频率在[0.4,0.6]内的概率为( )。
10.甲、乙两地举行数学联考,统计发现:甲地学生的成绩X~;乙 地学生的成绩Y~N(μ2,,图1 是 甲、乙两地学生的数学成绩正态曲线,则( )。
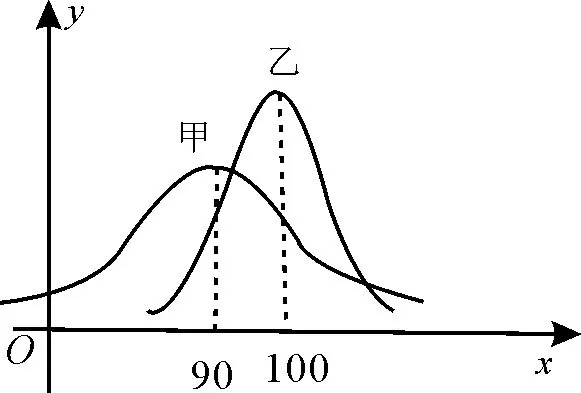
图1
附:若随机变量X~N(μ,σ2)(σ>0),P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3)。
A.甲地学生的数学平均分比乙地学生的高
B.甲地学生的数学成绩的离散程度比乙地小
C.若σ2=8,则P(92≤Y≤124)≈0.84
D.若σ1=4,则P(90≤X≤94)>P(82≤X≤90)
11.随着社会经济的不断发展,电子商务平台使人们购物更加方便快捷,假设电商平台的市场占有率和产品优质率的信息如表2。

表2
用A1,A2,A3分别表示某网民使用甲,乙,其他电商平台购物,B表示买到优质产品。若该网民在市场中随机选择一个电商平台,则下列说法中错误的是( )。
A.P1=P5
B.P1>P5
D.P0,P1,P2,…,P6中的最大值为P4
二、填空题(本题共4小题,每小题5分,共计20分。)
13.若随机变量X服从两点分布,P(X=1)=2P(X=0),则P(X=0)=_____。
14.随机变量X服从正态分布N(2,σ2),若P(2<X≤3)=0.36,则P(X>3)=____。
15.随机变量X服从以下分布表(表3)。
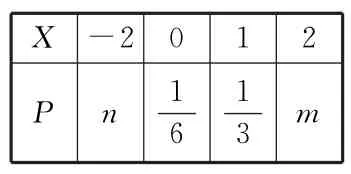
表3
若E(X)=0,则D(3X-1)=_____。
16.图2是一块高尔顿板示意图,在一木块上钉着若干排互相平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃。将小球从顶端放入,小球在下落的过程中,每次碰到小木钉后都等可能地向左或向右落下,最后落入底部的格子中,格子从左到右分别编写为1,2,3,4,5,用X表示小球落入格子的号码,则下列说法中正确序号为_____。

图2
三、解答题(本大题共6小题,第17题10分,其他题每题12分,共计70分。解答时应写出必要的文字说明、证明过程及演算步骤。)
17.(本小题10 分)假设有两箱零件,第一个箱内装有10 个,其中有2 件次品;第二个箱子内装有20个,其中有3件次品。现从两箱中随机挑选一箱,然后从该箱中随机取1个零件。
(1)求取出的零件是次品的概率;
(2) 已知取出的是次品,求它是从第一个箱子内取出的概率。
18.(本小题12 分)甲、乙两个选手进行围棋比赛,如果每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,随机变量Y表示冠军需要的比赛局数。
(1)求P(Y=2)的值;
(2) 那么采用3局2胜制还是采用5局3胜制对甲有利?
19.(本小题12分)如图3所示,小明家住C小区,在D学校学习。从家到学校有两条路线可供小明选择,L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为;L2路线上有B1,B2两个路口,各路口遇到红灯的概率分别为

图3
(1)若小明走L1路线,求最多遇到1 次红灯的概率;
(2)若小明走L2路线,求遇到红灯次数Y的数学期望;
(3)按照“平均遇到红灯次数最少”的要求,请你帮助小明从上述两条路线中选择一条最好的上学路线,并说明理由。
20.(本小题12分)某单位为了激发党员学习党史的积极性,现利用“学习强国”APP中特有的“四人赛”答题活动进行比赛,活动规则如下:一天内参与“四人赛”活动,仅前两局比赛可获得积分,第一局获胜得3分,第二局获胜得2 分,失败均得1 分。小张周一到周五每天都参加了两局“四人赛”活动,已知小张第一局和第二局比赛获胜的概率分别为,且各局比赛互不影响。
(2)设小张在这5 天内的“四人赛”活动中,恰好3天每天得分不低于4分的概率为f(p),求当p为何值时,f(p)取得最大值。
21.(本小题12 分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:g),质量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图4所示。

图4
(1)根据频率分布直方图,求质量超过505g的产品数量;
(2)在上述抽取的40 件产品中任取2件,设X为质量超过505 g的产品数量,求X的分布列;
(3)从该流水线上任取2件产品,设Y为质量超过505 g的产品数量,求Y的分布列。
22.(本小题12分)为了宣传航空科普知识,学校组织了航空知识竞赛活动,活动规定初赛需要从8道备选题中随机抽取4道题进行解答。假设在8 道备选题中,小明正确完成每道题的概率都是,且每道题正确完成与否互不影响;小宇能正确完成其中6道题,且另外2道题不能完成。
(1)求小明至少正确完成其中3 道题的概率;
(2) 设随机变量X表示小宇正确完成题目个数,求X的分布列及数学期望;
(3) 现规定至少完成其中3道题才能进入决赛,请你根据所学概率知识,判断小明和小宇两人中选择谁去参加市级比赛(比赛规则不变)会更好,并说明理由。

