基于Xgboost优化的KELM滑坡预报模型研究

李 璐，徐根祺，杨 倩，王艳娥，赵正健

(1.西安思源学院 理工学院，西安 710038；2.西安交通工程学院 机械与电气工程学院，西安 710030)

0 引言

滑坡灾害的发生是在自然演变或人为因素的影响下，一种复杂的非线性动力学演化过程[1]。滑坡灾害由于它本身高频发生、分布区域广泛及破坏力极强，对山区人民生命、财产有极大的威胁，对防灾减灾工作提出严峻的考验[2]。近年来国家相关部门和单位陆续出台相关政策，滑坡等地质灾害的课题也成为热门课题，相关学者对其研究也取得不错的成效。滑坡早期预报可以有效减少灾害的损失，影响滑坡发生的主要条件[3-4]：岩土条件、地质构造及地面地形的条件。近年来对滑坡的研究主要包括：1)通过地面调查结合遥感技术观察并分析滑坡全域地形地貌，分析成灾机理[5]；2)对滑坡易发区域地质构造分析滑坡形成的特征及成因，对滑坡滑动面失稳、变形及位移建模[6-7]；3)地面外界因素如暴雨、坡体、地震等综合影响，进行滑坡灾害的分析及建模[8-9]。

随着机器学习理论的发展，非线性模型被广泛应用在滑坡灾害预测的理论中[10]，赵晓萌[11]等从降雨量特征结合机器学习相关知识进行预测模型的建立；赵彬如[12]等从水文、气象阈值进行滑坡预测的研究，预测效果较好，但只适用于降雨型的滑坡灾害预测；胡欣等[13]将SVM-BP模型应用于降雨型的滑坡灾害安全评价的模型研究中，随后马娟、杨宗佶等[14-15]将多参数预警模式应用于滑坡预测中，同时李丽敏等[16-17]也将多影响因子作为滑坡位移预测模型的输入，针对滑坡灾害建模预报灾害的发生。针对滑坡体灾害概率预测及预警的相关研究目前存在以下不足[18]：地域成灾机理复杂，成灾因子单一，导致预测预警准确率低；预测模型容易陷入局部最优及模型本身的稳定性及适应性不足。本文针对这些问题分析滑坡全域地形地貌成灾机理并筛选因子，构造滑坡灾害预测模型，引入核极限学习机(KELM，kernel extreme learning machine)应用于滑坡预测预报中，改善极限学习机(ELM，extreme learning machine)奇点容易产生及隐含层数量确定问题，增加模型本身的稳定性及适用性，并使用高斯核函数(RBF，radical basis function)作为核函数进行模型建立。以研究区山阳县山区6种影响因子作为滑坡预测模型的输入，通过极限梯度提升树算法Xgboost(Xtreme gradient boosting)确定KELM模型中的参数惩罚系数及宽度参数，解决梯度决策树算法容易局部最优的问题，提高滑坡预测的精度。最后通过与其他预测算法进行比对，AUC均值、Precision、Accuracy及Recall都明显提升，体现出超参数优化后的模型在滑坡预测中较高的预测能力，给地质灾害研究带来活力及新思路。

1 Xgboost-KELM模型建立

1.1 KELM模型

ELM是一种单隐层的前馈神经网络，对于线性问题计算速度快且拟合能力也较好，但由于其隐藏节点存在随机映射特点，所以训练的模型稳定性和泛化性能力较差[19-20]。KELM在其基础上将核函数引入解决随机映射问题。针对于组不同的样本，ELM隐含层节点数用表示，激励函数用g(·)表示：

Hβ=U

(1)

(2)

H为隐含层的输出矩阵，β为输出权值矩阵，U为目标输出矩阵。

ELM学习过程中为提升稳定性及泛化能力，引入正则化系数C利用最小二乘法求解最优值[21]。

(3)

H+为H的广义逆。针对ELM解决多分类问题，依据KKT优化拉格朗日函数得到求解方案。当特征映射h(x)未知的情况得出ELM的输出函数：

(4)

对角矩阵用I表示，正则化系数用C表示，输出向量用U表示。依据Mercer’s条件，用核矩阵ΩELM代替随机矩阵HHT得出：

K(xi，xj)=h(xi)h(xj)=ΩELM(i，j)

(5)

得到KELM的输出模型为：

(6)

KELM中核函数会直接影响模型本身的性能。图1为RBF高斯核函数曲线图，x为分布中心偏移程度，sigma为分布的宽窄程度，当样本值接近分布中心x，对核函数值影响较大，反而影响较小，这与内积原理相似，可以通过距离衡量样本的相似性，高斯径向基核函数因其是局部核函数，所以局部学习能力强且只受相离较近样本点的影响，所以其对于一定范围内距离的样本可以在特征空间种线性分离预测较准确。文中选取RBF为核函数：

(7)

图1 RBF高斯核函数

核极限学习机在ELM的基础上引入了核函数，通过非线性映射到高维特征空间的方式将线性不可分的问题进行划分，进而提高了ELM性能。但由于核函数的引入，使得KELM算法对参数的选择非常敏感，所以引入Xgboost算法对KELM正则化系数C和核函数进行寻优，减少人为调参的复杂度，提高模型的准确性。

1.2 Xgboost优化算法

Xgboost[22-23]优化了梯度提升决策树，将原来针对错误样本分类中权值分配的不断迭代，改变为贪心策略，训练最佳方向是损失函数梯度下降的方向，最后通过加权求和的方法得出。并使用增加正则化优化了损失函数求解的方法，模型复杂度得到一定降低并防止了过拟合现象，模型精度得到一定程度的提升。

损失函数增加正则化，求解最优模型使用结构风险最小的思想[24]设置目标函数来寻优迭代模型，如公式(8)：

(8)

i为样本索引符号，I为样本总量，l为决策树的叶子节点数目，Yi为训练样本实际值。根据残差公式fn(Xi)=fn-1(Xi)+hn(Xi)，可得出fN(Xi)决策树训练(N=1，2，…，N)积累的残差及Ω(hn(X))针对Ω(h(X))在n次训练叶子节点得分，叶子节点得分ω用L2正则化的表示：

(9)

使用泰勒展开公式进行求解得到二次项，如式(10)：

(10)

并规定：

pi= ∂fn-1 (Xi )l(yi，fn-1(Xi))

(11)

最终得出目标函数如(12)所示：

(12)

用该目标函数进行模型最优解的求解，可以自己定义损失函数，对于模型构建的灵活性有极大的提升。由于Xgboost基于思想通过不断最小化目标函数迭代生成决策树，其预测偏差得到不断降低，综合两方面因素，Xgboost泛化误差得到整体降低，模型精度势必得到一定程度的提升。

2 模型应用

2.1 预测总流程

本文选取裂缝位移ΔX、岸坡水文地质条件H、土壤含水率D、土压力ΔF、斜坡倾角θ、及降雨量R6个滑坡诱发条件作为滑坡预测影响因子，监测数据通过数据预处理作为模型输入数据，通过Xgboost优化超参数C和并训练出 Xgboost-KELM模型，分别与GA及GC优化的KELM模型比对，最后通过验证集验证模型预测的结果。文中具体预测路线如图2所示。

2.2 样本数据选取

样本数据使用陕西省山阳县2018年3月到2020年3月的10个监测点数据作为数据集，样本集分为80%测试集和20%的两个验证集。模型输入数据：裂缝位移ΔX、岸坡水文地质条件H、土壤含水率D、土压力ΔF、斜坡倾角θ、及降雨量R6个滑坡体影响因子。预报模型训练及验证数集总共1 280组数据集。

表1 监测数据

2.3 数据预处理

监测数据来源于不同的采集传感器，由于环境的影响会出现一些缺失、离群或维度不统一的数据，对于模型的建立有极大的消极影响，因此需要对监测数据进行预处理。

2.3.1 异常值处理

监测数据中存在一部分偏离传感器本身范围的值或者偏离观测值较大的值，如果不处理会影响数据本身预测的准确性，如果距离达到5倍或者相距均值距离≥3倍标准差的数据为离群点。

2.3.2 缺失值的处理

监测数据通过多传感器传输，传输过程中经常会出现遗漏或者离群点情况，会损失有效信息，导致属性值确实。按照属性因素方法进行统计得出缺失率q，本文划分两种类别数据的缺失值，如表2所示。

表2 数据缺失值

2.3.3 数据归一化

采集的监测数据种类及数量都较大，多传感器数据量纲不同有较大的差异，原始数据直接建模对于预测的准确性影响极大，归一化处理公式如下：

(13)

式中，R为某因素归一化处理后的数据Rmin，和Rmax为某因素数据中最小值及最大值。图3为选取4个传感器中部分监测数据数据归一化前后的数据分布图，图中可以看出归一化前的数据跨度分布比较大，归一化后的数据在[0～1]量纲内，避免了数据本身量纲问题对预测模型的影响。

图3 监测数据归一化分布

2.4 Xgboost寻优的KELM模型

选取高斯径向基RBF 核函数，根据(6)和(7)两式可知需要优化的参数有正则化系数C和高斯径向基RBF 核函数中的核参数σ，其中C∈(0，a]，σ∈(0，b]。正则化系数C对模型方差、偏差、训练误差及测试误差都有较大的影响，具体影响如表3所示。核参数σ主要影响模型的拟合程度，当σ>0且较小时容易出现过拟合，相反σ>0较大时容易出现欠拟合。Xgboost优化的核极限学习机就是利用 Xgboost优化算法对 KELM 中的参数进行择优选取，从而提升 KELM 的性能，提高分类准确度，限制模型复杂度，缓解模型过拟合问题。为了避免多次枚举造成运算量过大，采用贪心算法寻求最优数结构，当Gain信息增益达到树的深度限制或Gain<0数停止分割，防止过拟合的前提下达到速度快拟合效果好。

表3 正则化参数C对模型指标影响

寻优具体流程如下：

STEP 1：数据标准化处理，划分训练样本；

STEP 2：初始化Xgboost算法参数；

STEP 3：Xgboost损失函数使用KELM模型中均方误差(MSE，mean-square error)代替，选择Xgboost目标函数下降最大点作为最佳切分点，对RBF 核函数参数σ及正则化系数C进行初始化；

STEP 4：将样本特征顺序排列，列出所有划分特征、特征值及score分值，根据TOP1分裂子树，同时计算分割的叶子节点的权重向量及信息增益；

STEP 5：判断是否达到数的深度限值或增益小于0，更新并保存最终叶子节点的权重值与增益值；

STEP 6：判断最大迭代次数的条件是否达到，如果满足条件则确定此时的σ及C参数为最优参数，基于最优参数构建Xgboost-KELM最优模型；不满足条件则返回执行STEP 4。

Xgboost参数设置：

1)通用参数

booster基学习器：gbtree(树模型)；

多线程：nthread；

迭代次数nround：1 000。

2)Booster 初始参数

eta：0.1，通过调整学习率调整模型最佳收敛速度；

min_child_weight：0，设置最小叶子节点样本的权重和避免出现过拟合现象；

max_depth：8，通过改变树的最大深度控制子节点分裂，避免出现过拟合现象；

gamma：节点分裂的依据，后损失函数下降值大于该值分裂；

subsample：0.7，对树随机行比例划分采样控制；

n_estimator：120，控制最大树的数量，防止数量大过拟合，数量小欠拟合；

lambda：1，L2正则化项；

Alpha：1，L1正则化项。

3)目标参数

objective：multi：softmax多分类问题；

eval_metric：[error，auc，mse]，回归模型。

2.5 仿真验证及结果分析

使用训练集进行训练Xgboost模型，当Xgboost找寻最优的分裂节点时，可以基于KELM损失函数迭代确定Xgboost最佳参数。图4为模型筛选最佳参数过程曲线图，a、b表示最大树数量与分类准确率关系，a为整个范围最大树数量分类过程，最大树数量n_estimator范围[1～1 000]，变化曲线先逐渐增加，增加至92棵树时上升缓慢，之后提升不明显渐渐趋于稳定；b为90～150棵树分类过程，随之n_estimator数量增加，会存在不到1%的下降趋势，当数量达到102棵树时分类准确率达到最高86.34%，取该数量为模型n_estimator最佳参数。c为树最大深度分类变化过程，max_depth范围为[1～10]，迭代过程可以看出深度为6时分类准确度最高达86.42%，max_depth最佳参数值取6；d为最小叶子权重变化过程，叶子节点的权重小于min_child_weight则停止拆分树，min_child_weight范围为[0～10]，曲线变化过程可以得出权重为2时分类准确率达到最高88.25%，min_child_weight最佳值取2。根据训练集训练结果得出Xgboost最终参数如表4所示。

图4 不同参数分类准确率

表4 Xgboost模型最终参数

为了获取KELM最优核参数σ及正则化C参数最佳组合，将测试集随机分为4组作为训练样本建立模型，参数的选值先从一个比较大的区间范围进行搜索，4组测试集验证后得出小范围[500，1 000]×[0.2，0.3]，之后进行多次迭代训练，当均方误差达到最小值时，取此时参数核参数σ及正则化C为最佳组合参数。图5为4组测试集训练过程的均方误差迭代曲线，数据集4收敛速度最慢，数据集2、3均方误差较低但收敛速度在迭代次数12出现饱和，而数据集3均方误差及收敛速度相比其他数据集表现最佳，均方误差最低达到并稳定于1.187×10-3。且在7次迭代收敛饱和。所以选取数据集3训练参数为模型最佳参数，σ=0.262 4，C=703.24。

图5 不同测试集的均方误差

为验证模型的稳定性及适应能力，通过模型在新样本集中的适应度、准确性及方差偏差验证。方差表示模型每次预期结果与实际结果的误差的稳定情况；偏差值表示每次预期结果与实际结果的偏差。模型误差包括方差、偏差及其他无法避免误差，图6为偏差及方差示意图。预测模型最佳选择顺序：1)方差小，偏差小；2)方差小，偏差大；3)方差大，偏差小；4)方差大，偏差大。

图6 偏差及方差示意图

精确率：在预期的正样本中实际结果也为正样本的占比。

precision=TP/(TP+FP)

(14)

准确率：准确率表示所有的预测样本中，预测正确的占比。

Accuracy=(TP+TN)/(TP+FP+FN+TN)

(15)

召回率：预测结果准确的正样本占所有正样本的比例。

recall=TP/(TP+FN)

(16)

AUC：通过计算ROC曲线与坐标轴围成的面积得到，介于[0.5，～1]之间，预测的真实性取决与AUC值接近1的程度，靠近1真实性高反之则反。

(17)

真正率：预期正样本数/实际正样本数。

(18)

假正率：预期为正的负样本数/实际负样本数。

(19)

实验采用KELM作为滑坡灾害预测模型，并用Xgboost优化算法中的超参数寻优。使用同一个验证集验证GC及GA优化KELM模型预测效果比对。表5为在验证集1中128个数据中各模型输入相同数据得出的预测结果的混淆矩阵对比表。

表5 不同模型混淆矩阵对比表

图7为3种模型同一评价指标的对比图，柱状图的差异可以对比得出各个预测模型对应评价指标的好坏，从而反映预测模型性能的优劣。4个评估参数中，Xgboost优化KELM均明显优于GA和GC优化的模型。本文的Xgboost-KELM模型AUC均值为0.985，相比GC优化高约3个百分点，比GA优化高6个百分点。其他指标Precision、Accuracy及Recall高于另外两个模型百分比[1.7～7]范围之间。实验结果说明Xgboost-KELM模型具有较好的预测效果，在滑坡灾害预测中有较好的预测能力。

图7 评价指标对比图

图8为验证集2中打乱随机抽取的128个监测数据使用Xgboost优化KELM模型后的实际发生概率与预测发生概率比对图。图中实际值与预测值基本吻合，拟合情况较好。极限的几个数据27、38、89及111发生概率存在一些差异，但是对应风险等级都属于同等级风险。准确率达到98%。引入Xgboost对KELM参数值进行优化，实际预测精度较为理想。并使用验证集2进行各模型稳定性计算，Xgboost-KELM有较小的方差且偏差也较小，属于最稳定的“方差小、偏差小”模型，稳定性能最强，而GC-KELM介于“方差大、偏差小”与“方差大、偏差大”之间，模型不稳定，GA-KELM属于“方差大、偏差大”，模型最不稳定。

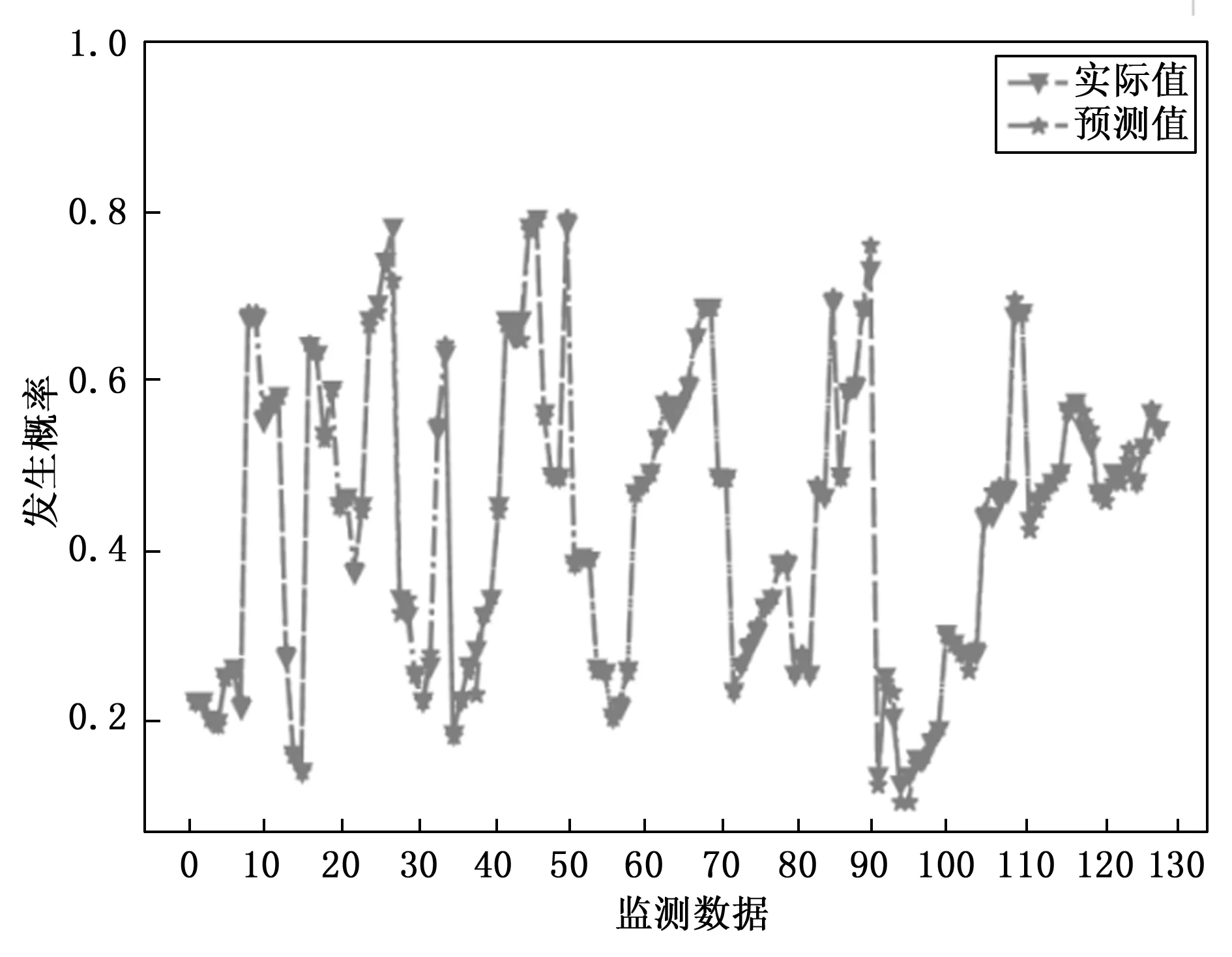
图8 Xgboost优化模型预测结果

3 结束语

本文针对山阳县研究区域的数据使用基于Xgboost优化KELM模型建立滑坡灾害预测模型，通过仿真研究分析滑坡影响因子与发生概率之间关系，并与GA-KELM及GC-KELM建模结果进行比较。

1)选用RBF高斯核函数的极限学习机模型较好地解决了ELM适用性及稳定性不佳的问题；

2)使用KELM模型中均方误差MSE作为损失函数，训练模型并选择目标函数下降最大点作为最佳切分点，确定最佳参数；并使用Xgboost寻优算法对核函数中的正则化系数C和核函数σ寻优，通过4组测试集的均方误差迭代曲线得出最佳超参数，建立Xgboost-KELM模型，并与GA及GC优化KELM建模进行比较；

3)通过几种模型的样本集1对比验证，结果表明Xgboost-KELM具有较高的Precision、Accuracy及Recall和AUC值，同时使用新样本集2验证稳定性及泛化能力，结果表明该模型稳定性较好，进一步证明该模型的应用能有效提高滑坡灾害的预报概率，对滑坡灾害提前预警，降低自然灾害造成的损失具有重要意义。