空间几何体中最值问题的常用求法
■廖子宜
立体几何中的最值问题主要与空间图形的距离、角、面积、体积有关,是高考命题的热点。此类问题涉及知识面较广,灵活性较大,常用的求法有:二次函数性质法、基本不等式法、射影法、两点之间线段最短法、垂线段最短法、三角函数性质法等。
一、二次函数性质法
例1如图1,一个圆锥的底面半径为2cm,高为6cm,其中有一个高为xcm 的内接圆柱。当x取何值时,圆柱的侧面积最大?等式逆用为:a,b∈R+,当且仅当a=b时等号成立。
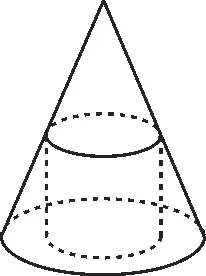
图1

三、射影法
例3如图2,棱长为1 的正方体ABCD-A1B1C1D1中,若G,E分 别 是BB1,C1D1的中点,点F是正方形ADD1A1的中心,则四边形BGEF在正方体侧面及底面共6 个面内的射影图形的面积的最大值是
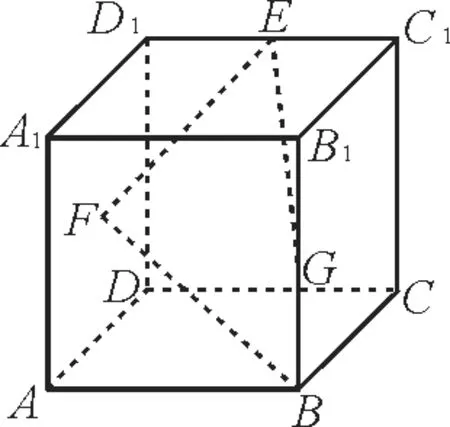
图2
____。
解:显然,四边形BGEF在前后侧面上的射影图形的面积相等。易知点E在前面平面上的射影是A1B1的中点E1,点F在前面平面上的射影是AA1的中点F1,可得四边形BGE1F1的面积为。同理可得,四边形BGEF在左右侧面上的射影图形的面积相等且等于;在上下底面上的射影图形的面积相等且等于。故四边形BGEF在前后侧面上的射影图形的面积最大,其最大值为。
评注:解题的关键是找到四边形BGEF四个顶点在各个面上的射影点的位置,再根据正方体的性质计算其面积。
四、两点之间线段最短法
例4如图3 所示,已知圆柱的高为80cm,底面半径为10cm,轴截面上有P,Q两点,且PA=40cm,B1Q=30cm,若一只蚂蚁沿着侧面从P点爬到Q点,则蚂蚁爬过的最短路径长为_____。
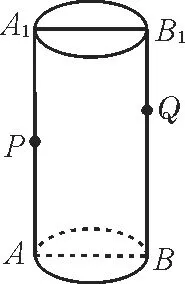
图3
解:将圆柱侧面沿母线AA1展开,得到如图4所示的矩形。
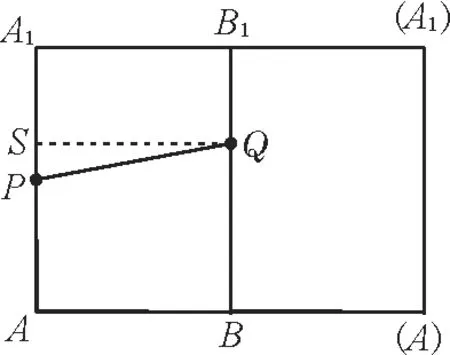
图4
易得A1B1=10π。过点Q作QS⊥AA1于点S,在Rt△PQS中,PS=80-40-30=10,QS=A1B1= 10π,所 以PQ=,即蚂蚁爬过的最短路径长是cm。
评注:求几何体表面上两点间的最小距离,可将几何体沿着某棱(母线)剪开后展开,画出其侧面展开图,把求曲线长问题转化为求平面上的线段长问题。
五、垂线段最短法
例5如图5,在棱长为2 的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,则点P到直线CC1的距离的最小值为______。
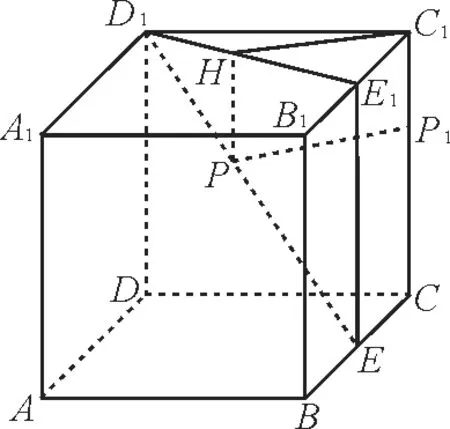
图5
解:过E作EE1⊥底 面A1B1C1D1交B1C1于E1,过P作PH⊥D1E1于H。连接C1H,作PP1⊥CC1于P1。
易知四边形PP1C1H是矩形,点P在线段ED1上运动,点P到直线CC1的距离是C1H。当C1H为 Rt △C1D1E1的 底 边D1E1上的高时,C1H最小,记高为h。

评注:当点P在D1E上移动时(不含端点),四边形PP1C1H一定是矩形;当点P与D1或E重合时,点P到直线CC1的距离的最小值为C1D1或CE,此时显然不是最小值。
六、三角函数性质法
例6如图6 所示,边长AC=3,BC=4,AB=5 的三角形简易遮阳棚,其A,B是地面上南北方向两个定点,正西方向射出的太阳光线与地面成30°角,当遮阳棚ABC与地面的夹角等于____时,才能保证所遮影面ABD的面积最大。
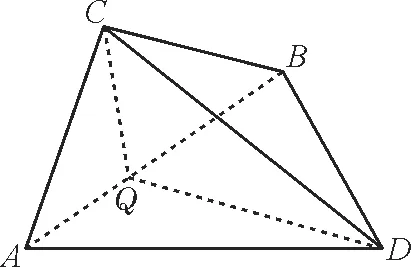
图6
解:易知△ABC为直角三角形。在平面ABC内,由C向AB引 垂 线,垂 足 为Q,则DQ为CD在地面上的射影,且AB⊥平面CQD。因为太阳光与地面成30°角,所以∠CDQ=30°。


