一种改进的粒子群算法在交通分配上的应用

李晓君,赵晓蕾,赵洪銮,3,宿梦梦,邹 炜

(1.山东建筑大学 计算机科学与技术学院,山东 济南 250101;2.山东建筑大学 建筑城规学院,山东 济南 250101;3.天津城建大学 理学院,天津 300384)

0 引 言

交通拥堵加剧导致的出行成本大幅提高、交通事故增加、环境污染和能源消耗等问题愈发严重,缓解交通拥堵成为当下亟待解决的难题。目前缓解交通拥堵的有效途径是结合智能交通系统(ITS)智能技术和动态交通分配(DTA)模型对交通流量进行合理管理和分配。

动态交通分配模型是ITS的核心,交通分配是动态交通分配的基础,其求解常用粒子群算法。粒子群优化算法(PSO)是Eberhart和Kennedy[1]基于鸟类的觅食行为提出的一种随机搜索算法,是基于群体的启发式优化算法。粒子群算法在具有原理简单、没有变异等复杂操作且能应用于大多数优化问题的求解等优点的同时,也存在迭代后期收敛速度慢、精度低和易陷入局部最优等问题。针对这些问题,研究者设计了不同的改进策略。Wang等[2]将自适应学习策略引入粒子群算法,同时加入潜在预测策略来预测候选粒子在各个维度引导种群的能力,以此提高算法的收敛速度;张晓莉等[3]使用神经网络中神经元的非线性作用函数作为权重建立模型,提高了算法的稳定性及收敛速度;杨红[4]将天牛须搜索算法与粒子群优化算法结合,并利用Logistic混沌映射对粒子速度及位置进行初始化,有效提高了算法的精度;李荣雨[5]将布谷鸟算法中的莱维飞行策略引入到粒子群算法,利用莱维飞行进一步更新个体的位置,有效提高了算法的优化性能;梁田等[6]将基于相似度及聚集度分析的莱维飞行引入粒子群算法,能够有效帮助粒子逃离局部最优。

该文使用舍弃速度项的简化粒子群算法对用户最优的交通分配模型进行求解,简化的粒子群算法可以有效避免迭代后期速度过于发散导致的收敛速度慢等问题;同时,使用自适应线性惯性权重来消除粒子惯性分量的不良影响;此外,为了避免迭代后期陷入局部最优的问题,通过莱维飞行机制来改变粒子位置,帮助粒子脱离局部最优,以此提高算法精度。

1 粒子群算法

1.1 标准粒子群算法

标准粒子群算法的核心是速度和位置更新公式,如式(1)、式(2)所示。

(1)

(2)

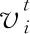
Shi等[7]在粒子的速度更新公式中加入惯性因子ω,更改后的公式如式(3)所示。

(3)

随后,Shi等[8]又更改固定权重为线性递减惯性权重,其给出的惯性权重公式如式(4)所示。

(4)

式中,ωmax和ωmin分别表示最大和最小加权系数,经实验确定,惯性权重取值在[0.4,0.9]上时算法性能较好,故ωmax一般取0.9,ωmin一般取0.4;tmax表示最大迭代次数,t表示当前迭代数。

标准粒子群算法的步骤如下所述:

Step1:初始化。随机初始化粒子速度和位置。

Step3:更新。根据公式(1)和(2)更新粒子的位置和速度。

Step5:将各个粒子的适应度值与全局最优位置gbest的适应度值进行比较,若有比当前最优位置gbest好的粒子,即有粒子的适应度值要优于gbest的适应度值,则存储该粒子位置,并将该粒子的位置作为新的gbest。

Step6:判断粒子是否达到最优或是否达到最大迭代次数,若达到条件,则终止迭代,否则执行Step3。

1.2 简化的粒子群算法

胡旺等[9]提出了简化的粒子群算法,算法舍弃了粒子群的速度项,仅以粒子的位置项来控制粒子进化方向,可以有效避免迭代后期粒子速度过大时出现的粒子过于发散的问题,且通过实验证明,简化的粒子群算法更加高效。

式(2)和式(3)简化合并后可得到简化粒子群算法的位置更新公式,也是该算法的核心公式:

(5)

该文使用简化的粒子群算法,同时引入自适应的线性惯性权重,以此减弱权重份量对算法求解质量的影响。此外,为了提高粒子群在迭代后期的搜索能力、有效改善或避免粒子群陷入局部最优,引入莱维飞行策略,通过莱维飞行来改变粒子位置。具体的改进策略将在下面的章节进行介绍。

2 粒子群算法改进

2.1 自适应惯性权重

在算法迭代前期,惯性权重应取较大值,粒子可以在更大范围内进行搜索,以快速确定全局最优位置所在区域;在算法迭代后期,惯性权重应取较小值,通过小范围内的搜索来获取精度更高的解。因此,权重呈现在迭代前期保持较大数值、迭代中期可以迅速递减且在迭代后期保持较小,即呈“倒S”形变化,是一种比较理想的惯性权重选取方案。

Sigmoid函数常被用作神经网络的激活函数,其定义为:

(6)

Sigmoid函数是一种典型的S型函数,其图像如图1所示。

图1 Sigmoid函数

文献[10-11]使用的非线性动态递减的惯性权重和联合进化离散度的非线性动态自适应惯性权重因子如式(7)、式(8)所示:

(7)

式中,rand为[0,1]间的随机数。

ω=ωmax+(ωmin-ωmax)·

(8)

式中,b表示阻尼因子,一般取值为[0,1],k(t)为种群进化离散度参数。

根据式(7)、式(8)和Sigmoid函数对权重公式进行改进,改进后的公式如式(9)所示:

(9)

式中的系数通过多次实验所得,当系数分别为10和5时,权重ω的变化如图2所示,满足对系数呈现先大后小的预期。

迭代2 000次时,权重ω的变化如图2所示。

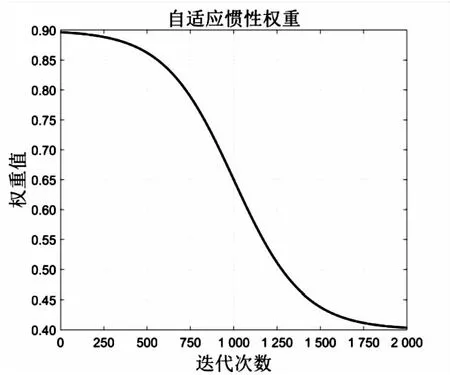
图2 自适应惯性权重变化曲线

2.2 莱维飞行

莱维飞行是一种服从重尾分布的随机游走的过程,它可以用更短的距离和更少的步数来搜索更大的面积。莱维飞行在优化领域应用广泛,当算法陷入局部最优时,可以用莱维飞行的公式重新调整粒子的位置来逃离局部最优。

莱维飞行轨迹如图3所示。

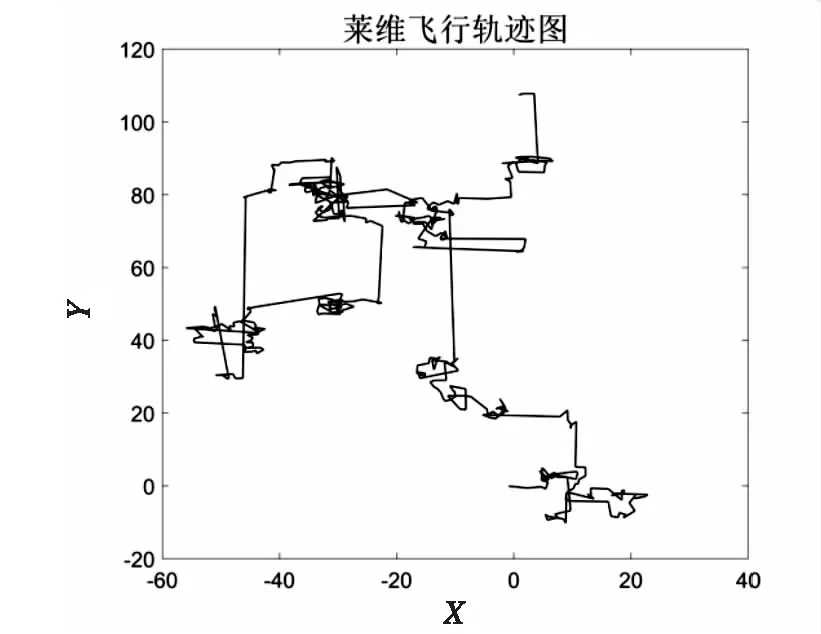
图3 莱维飞行轨迹

基于莱维飞行策略的位置更新公式如式(10)所示。

(10)

式中,a表示步长因子,其值大于0;⊗表示点对点乘法。

目前生成服从莱维分布随机数常用的方法是Mantegna方法,其生成随机步长s的方法如式(11)所示。

(11)

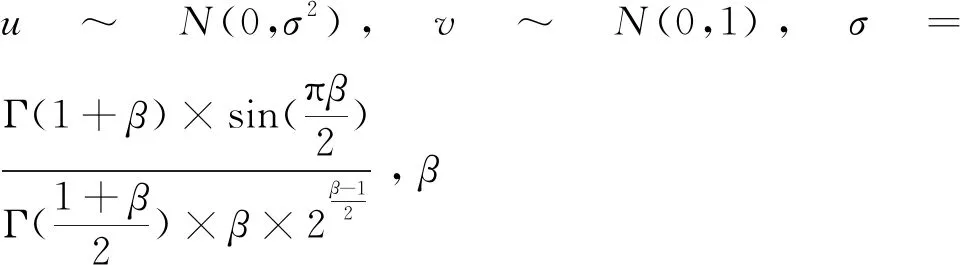
2.3 仿真实验

为了验证改进算法的性能,选择Sphere、Rastrigin、Griewank和Ackley四个测试函数对改进的算法(SNL-PSO)与权重固定的粒子群算法、标准粒子群算法和使用非线性随机性权重并引入莱维飞行的粒子群算法进行对比,函数的取值范围、理论最优解和定义如表1所示。

表1 测试函数取值范围、最优值及定义

c1和c2均设置为2,固定权重的粒子群算法的权重值设置为0.9,维度D设置为30,粒子种群数N设置为80,迭代次数G设置为1 000,仿真实验结果如表2～表5所示。

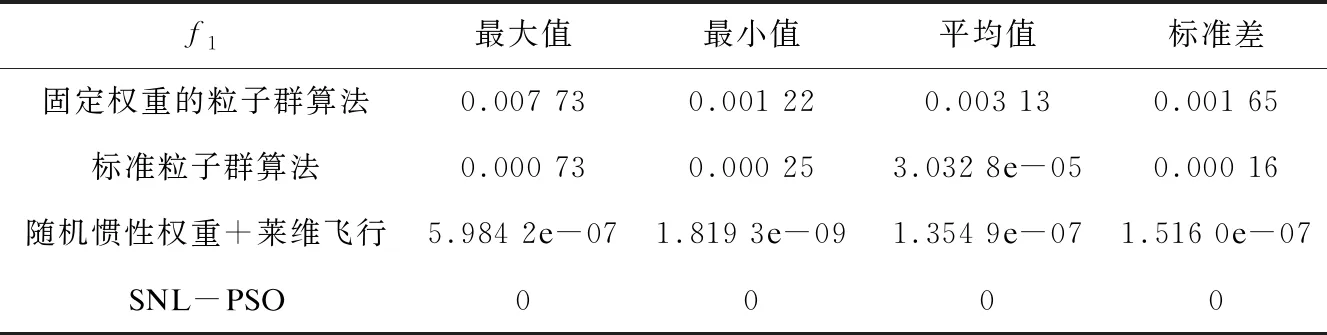
表2 Sphere函数仿真结果

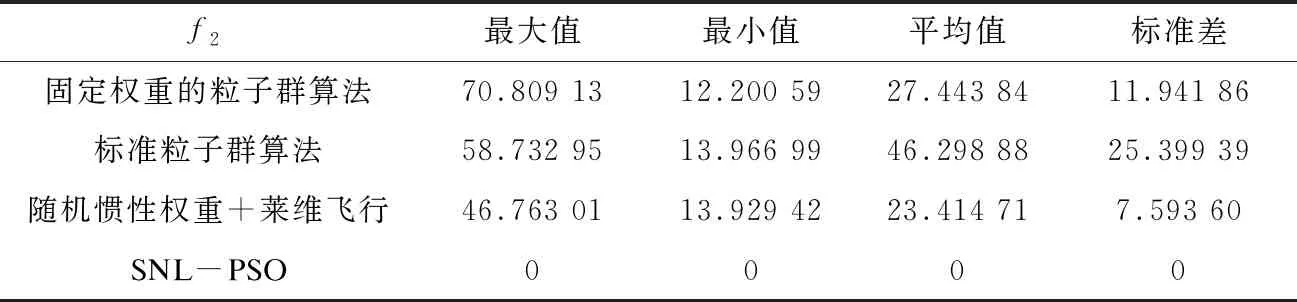
表3 Rastrigin函数仿真结果

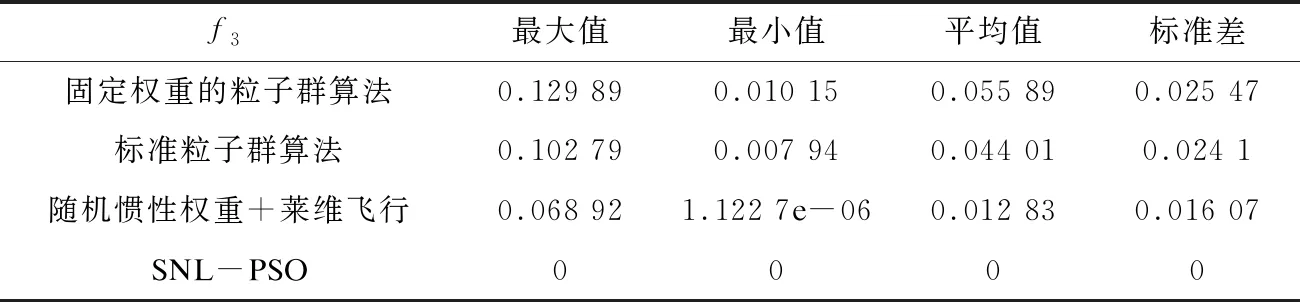
表4 Griewank函数仿真结果

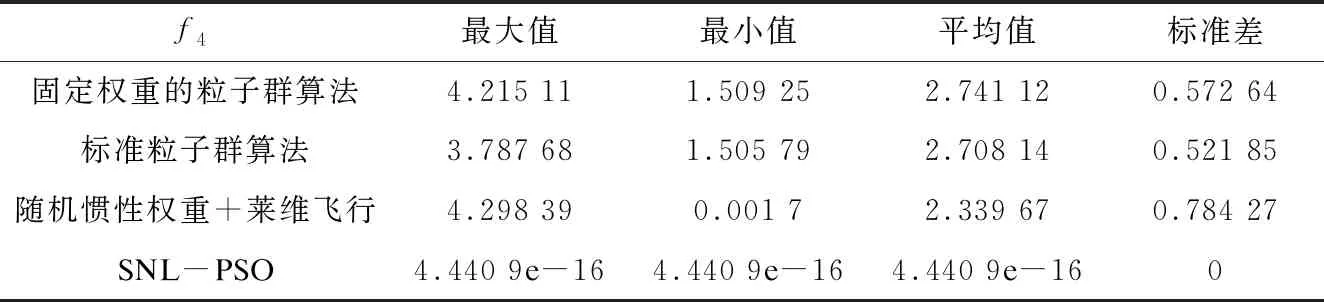
表5 Ackley函数仿真结果

四个测试函数的仿真结果曲线如图4所示。

(a)Sphere函数 (b)Rastrigin函数

从Sphere、Rastrigin、Griewank和Ackley四个标准测试函数的仿真结果中可以看出,使用带有随机性惯性权重并引入莱维飞行机制的粒子群算法精度有所提升,但收敛度和稳定性改动不大,而在此基础上舍弃速度项的粒子算法精度有明显提升。同时,从四个标准测试函数的仿真结果曲线中也不难看出,改进后算法的收敛度和稳定性也明显优于其他两种算法。

3 交通分配

3.1 用户最优交通分配模型

基于最优控制理论的交通分配模型,根据交通流量分配目标的不同可以分为用户最优模型和系统最优模型,前者以出行者的出行成本最小为目标,后者以系统总成本最小为目标,由于前者更能反映当下出行者择路行为,该文建立并求解用户最优模型。

用户最优模型数学表示如式(12)所示:

(12)

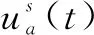
3.2 仿真实验

3.2.1 仿真案例路网图

文献[12-16]分别使用了不同改进策略的粒子群算法求解动态交通分配问题,实验结果证明相比传统的数值算法,粒子群算法有更优越的求解性能。该文使用上述的改进粒子群算法对图5所示的算例进行仿真实验。

图5 算例模型

图中仅有(1,12)一个OD对,共十条路径,路段上的数字表示车流量为0时在该路段的运行时间,路径的集合可用如下的矩阵表示:

(13)

使用经典BPR阻抗函数作为路段阻抗函数,其公式如下:

(14)

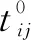
3.2.2 仿真结果

当总交通流量为2 000时,分别使用标准粒子群算法和改进后算法进行交通分配得到的各个路径上的分配结果如表6所示。

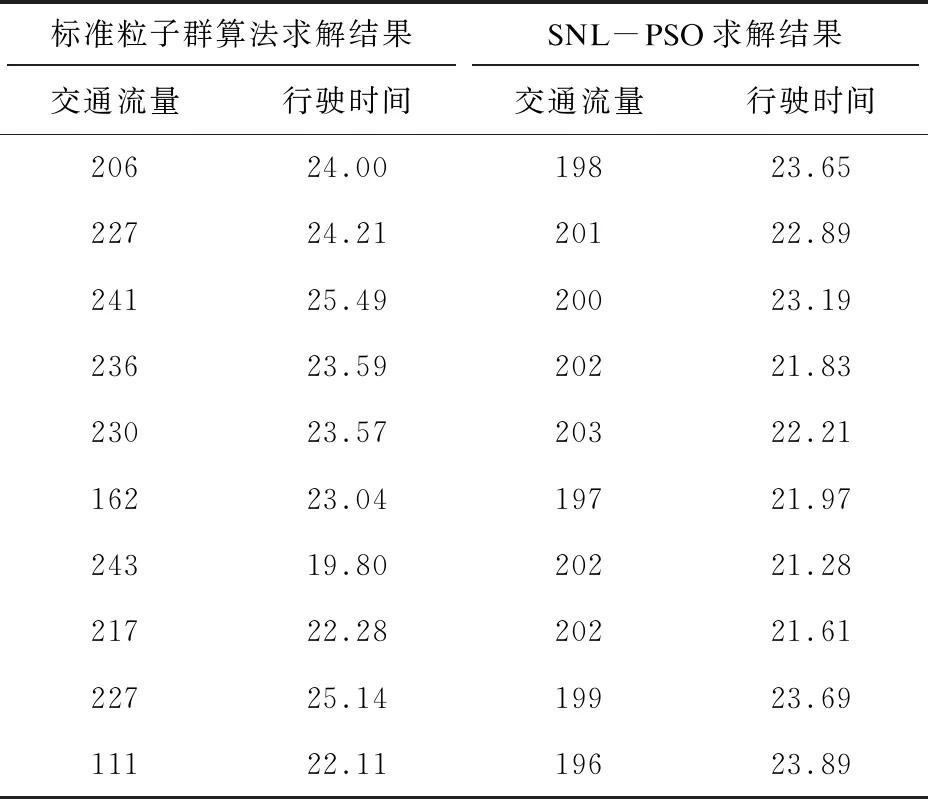
表6 交通量分配结果

分配后得到的各个路径上的阻抗时间如图6所示。

图6 各个路径上的阻抗时间

由图6可以看出,改进后的粒子群算法的分配曲线波动更小,更加平缓,且多数路径上的阻抗时间都有所降低。

由表6可得,相对于标准的粒子群算法,改进后的粒子群算法对各个路径上的车辆分配更加均衡,且各个路径上的时间波动相比较于标准的粒子群算法更加稳定,可以有效避免某个路径上车辆过多而导致车辆拥堵现象的发生。实验结果验证了改进后的算法在交通分配上的可行性和有效性。

4 结束语

简单介绍了标准粒子群算法和简化的粒子群算法,并在简化粒子群算法中引入了整体呈现下降趋势的带有随机性的惯性权重和莱维飞行策略,以此来提高算法精度和提高算法的收敛性。通过测试函数模拟发现,改进后的算法收敛速度更快且解的精度更高。

而后,将改进后的算法应用于单一OD对多路径路网的用户最优模型的求解上。对于算法中其他参数初始值的设置对算法性能的影响、莱维飞行概率的调整以及将算法更好地应用于大规模路网上的动态交通分配模型求解上仍需要做进一步研究。