基于新型多可信度代理模型的多目标优化方法

赵欢，高正红，夏露

西北工业大学 航空学院，西安 710072

现代飞行器外形设计需要考虑复杂的飞行条件/作战环境、多个飞行状态和高的性能表现，设计要求越来越多且更加苛刻，已成为典型的多目标复杂约束优化问题。比如高速旋翼翼型优化不仅要考虑前飞、悬停和机动等多个状态下升阻特性和力矩特性等10 余项设计指标要求；同时随着飞行速度提高，要考虑的状态范围更宽（Ma=0.2～0.9），设计要求变高，各个指标间的矛盾更加突出，设计空间也更加复杂，因此，需要采用复杂多目标优化模型。此外，随着多学科协同设计开始广泛应用于飞行器设计，如战斗机气动/结构/隐身/音爆等各个学科的设计要求以及单个学科内亚、跨、超声速多个状态点的设计要求，会使得设计目标和设计约束进一步增多，面临高维多目标设计难题。目前以NSGA-Ⅲ为代表的经典多目标优化算法仅对2～3 个目标具有良好的搜索能力[1］，过多的目标会导致算法的收敛性和多样性急剧下降。这是因为首先随着目标个数m的增加，近似整个Pareto 前缘点的个数呈指数增加（m-1 维超曲面），巨大数量的Pareto 解导致高的计算花费。其次非支配解比例指数增加（非支配解比例为1-2/2m），几乎所有的粒子都变成非支配的，过高的非支配解比例会使得目前的多目标进化算法很难选择具有优势的个体，种群的进化压力下降，甚至变为随机搜索算法，收敛性严重变差，而随着目标个数增加，种群数增大，使得进化算法选择非支配解和保持多样性的计算复杂度剧烈增加[2］。最后，大于3 个目标的Pareto 前缘可视化问题也给设计决策者带来了极大困难，选择折衷解需要更多的时间。这类问题也被统称为高维多目标优化问题。目前流行的多目标算法对于3 个及3 个以上目标问题的扩展性降低，即便是对于简单的Pareto 面。

自从2003 年进化多目标国际会议[3］召开后，许多研究者对高维多目标问题进行了深入研究，并提出了一系列可行的解决策略。针对第1 类问题，即高维多目标导致现有基于Pareto 支配的多目标进化算法搜索能力下降，收敛特性变差的问题，可以通过以下方法解决：① 修改Pareto 支配方式以减少非支配解的数量[4］；② 使用不同的排序方法选择非支配解[5-6］；③ 新的适应值评价机理，而不是传统的Pareto 支配[7］；④ 评价指标方法的使用，比如超体积评价指标[7］，但随着目标增加，计算复杂度指数增加；⑤ 将多目标问题转化为大量的标量化函数优化问题，例如使用权重总和方法、切比雪夫度量和法向边界交叉（NBI），以及使用分解基于多目标优化算法（Multi-Objective Evolutionary Algorithm Based on Decomposition， MOEA/D）等将多目标问题转化为多个单目标优化问题[8-10］，然而生成真实Pareto前缘均匀分布或偏好分布点的权重向量却很难选择。针对第2 类问题，即Pareto 前缘解集数量指数增加的难题，可以通过以下方法解决：① 引入偏好信息，使多目标搜索集中在Pareto 前缘的一个小区域[11］；② 目标降维方法，通过分析目标之间的相关性，去掉冗余目标，仅优化目标中最冲突的1 组以使其产生和原始问题相同的Pareto前缘解。目前流行的一些目标降维方法如下：① 支配关系守恒方法，即移除某个目标后支配关系保持不变[12］；② 无监督特征选择方法[13］，通过测量目标之间的相关性，将距离更远的目标列为更冲突的一些；③ 主成分分析方法[14］，通过线性主 成 分 分 析（Principal Components Analysis， PCA）降维去掉冗余的目标；④ Pareto 角搜索进化[15］算法和几何投影法等。目标降维方法不仅能解决以上2 类问题，还能解决可视化难题，因此是目前高维多目标问题的主要解决途径。

尽管上述许多算法已经在试图解决高维多目标优化问题，但有许多缺乏在实际工程问题中的验证。其中，结合PCA 降维分析和多目标进化算法已经得到了许多设计者的使用，并取得了良好的效果，比如超临界翼型、旋翼翼型以及飞翼翼型多学科多目标优化设计等[16-17］。然而，目标降维方法仅当目标中存在较强相关性的目标，即多个冗余目标时，才能起作用。并且一些线性降维方法如PCA 主要针对二阶及二阶以下相关性的目标维数减少，缺少对更高阶以及一般问题的适应性。Saxena 等[18］引入了PCA 和非线性主成分分析（Nonlinear Principal Component Analysis，NPCA）结合的降维方法，在一些测试函数上，相对于支配关系守恒降维方法，计算复杂度更低。可见，高维多目标优化问题，即如何高效地找出高维空间中真实Pareto 最优解，依然困扰着设计者，尤其对于包含很少甚至不含冗余目标或相关性强的目标集合，困难更大。

1 刚性共轴双旋翼直升机桨叶翼型高维多目标优化难题

直升机需要兼顾前飞、悬停和机动等各种性能要求。对单旋翼直升机而言，前行桨叶和后行桨叶需要同时提供拉力并使其合力作用于转轴处，以维持直升机机身平衡，因此需要旋翼翼型兼顾低速高升力和高速低阻力特性。而对于刚性共轴双旋翼直升机，在飞行时存在2 幅旋翼的对转运动，桨盘两侧同时存在前行桨叶，合力自然作用于转轴处，前行桨叶的高动压保证了足够的拉力，后行桨叶可不用提供拉力；在直升机高速前飞时，可将后行桨叶卸载以避免大范围反流区引起的阻力、噪声激增等问题，因此此类直升机可以大幅提高前飞速度。前飞速度的提高，使桨叶外侧段翼型需要保持更高的阻力发散马赫数和高速低阻特性，相对于单旋翼翼型，设计要求更加严苛。根据需求，此类高速旋翼翼型桨尖（0.9R～1.0R 处，R 为桨叶半径）性能要求如下：

1）高速前行时，桨尖翼型工作状态马赫数超过0.87，波阻急剧增加，前飞需用功率增加，设计翼型应具有高的零升阻力发散马赫数，尽可能低的零升阻力系数，以及维持低的零升俯仰力矩系数。桨尖载荷要求可适当降低。

2） 在 跨 声 速 状 态 范 围 内(0.8 ≤Ma ≤Madd0，Madd0为零升阻力发散马赫数)，激波位置和强度随马赫数等状态变化非常敏感，设计翼型在此范围内应该具有稳健的气动表现。

3）悬停状态下，要求翼型在中等马赫数下提供高升阻比以减小需用功率。例如在设计马赫数范围内(Ma=0.4～0.6)，要求具有高的升阻比。

4）机动飞行时需要高的载荷系数，尤其是后行桨叶一侧，在大迎角范围内极容易出现失速颤振现象以及升力特性的突然下跌，致使力矩变大，飞行包线减小。因此，在低马赫数范围内(Ma=0.2～0.4），应具有高的最大升力系数和最大升阻比，以提高其机动性能。

5）在所有马赫数范围或整个飞行包线范围内，各剖面设计翼型应具有极低的俯仰力矩系数以减小桨叶扭转及控制系统的操纵载荷。

6）一些研究表明，在桨叶表面近似0.45R～1.00R 区域内，层流区能稳定存在，并且可以显著提高升阻比。因此，这个区域内翼型可以使用自然层流超临界翼型设计。

以上这些指标要求达10 余项之多，并通常是相互矛盾和制约的，面临高维多目标和复杂约束优化难题。因此，发展高效的高维多目标设计模型和设计方法，并设计满足严苛设计要求的刚性共轴双旋翼直升机翼型非常重要。

高维多目标优化问题可以数学定义为

式中：定义了m 个目标{ f1(X)，f2(X)，…，fm(X) }，p 个不等式约束gi(X)以及q 个等式约束hj(X)的优化问题。代表n维设计变量。XL和XU分别为设计变量下边界和上边界。实际优化中等式约束hj总可以转化为不等式约束，即

式（2）为仅考虑设计点气动特性的确定性优化设计模型，无法兼顾非设计点的气动特性，如来流马赫数变化时的气动特性。

如果考虑飞行状态等各种不确定源对翼型气动特性的影响，将式（2）模型直接修改为

式中：Ξ=[ ξ1，ξ2，…，ξi]表示各种可能的不确定源，如马赫数和升力系数。本文假设所有的不确定源ξi为独立的连续概率分布变量。很显然，由于Ξ 为满足一定概率分布的不确定变量，对式（3）模型直接优化很难获得在Ξ 可能的各种变化值后仍然保持稳健气动特性的翼型。因此，式（3）模型很难考虑各种不确定源的影响，也无法满足工程使用需求。为了使刚性共轴双旋翼直升机翼型在高速状态下保持稳健的气动特性[19-21］，基于连续概率理论，将式（3）模型转变为稳健多目标优化模型，即

式中：μfi(X，Ξ)和σfi(X，Ξ)分别代表目标fi(i=1，2，…，m)基于不确定变量Ξ 影响的均值和方差；μgi(X，Ξ) 和σgi(X，Ξ) 分 别 代 约 束gi(i=1，2，…，p)基于不确定变量Ξ 影响的均值和标准差；μhj(X，Ξ)则代表约束hj( j=1，2，…，q)基于不确定变量Ξ 影响的均值；参数k 取值越大则约束可靠性越强，反之亦然。式（4）模型为确定性优化模型式（2）在考虑多源不确定性影响后建立的稳健优化设计模型。在得到连续随机变量Ξ的概率密度函数ρ(Ξ)后，可以通过积分方式得到目标函数和约束函数的统计特性，目标函数fi的均值和方差为

式中：ΞU和ΞL分别代表随机变量Ξ 的变化上限和下限。

相对于传统的确定性多目标优化，稳健多目标优化引入了各个目标表现和稳健性，以及各个约束的可行稳健性测量。因而目标个数成倍增加，优化可行域变窄且更加复杂，函数评估数量增加。目前一些经典的多目标算法如NSGA-Ⅲ等对于高维多目标（目标个数超过3 个）问题，其搜索和收敛能力均下降，尤其一些冗余的目标会影响算法的收敛效率和真实表现。因此，通过有效的目标降维方法结合目前经典的多目标算法，将能有效解决高维多目标难题。同时，基于前期发展的多可信度代理建模技术（Adaptive Multi-Fidelity Polynomial Chaos-Kriging， AMF-PCK），本文提出了高效的高维多目标稳健优化平台，以满足工程使用。

2 自适应多可信度多项式混沌-Kriging 代理模型

相 对 于Universal Kriging、Blind Kriging 和Dynamic Kriging， LAR-PC-Kriging （Least Angle Regression -Polynomial Chaos Expansion -Kriging）不仅具有更好的自适应基函数选择策略，同时由于多项式混沌展开提供了完备的正交基，理论上多项式混沌对不同的问题能提供更好的近似能力和更强的适应性。然而，由于目前自适应基函数选择方法受样本数的影响[22］，当有限甚至非常少的样本可利用时，LAR-PC-Kriging模型不能正确选择一组最优的多项式基函数，导致其近似能力可能比Universal Kriging 更差[23］。结合多可信度建模技术，本文提出了一种更加高效的代理建模途径，即自适应多可信度多项式混沌-Kriging （AMF-PCK）代理模型[24］。

AMF-PCK 在任意点X 的预测值为

式中：α0为缩放因子；yc(X)是对低可信度多项式混沌展开（Polynomial Chaos Expansion， PCE）矫正修正项；C(X)为定义的第2 个高斯过程；zh(X )为零均值的静态高斯随机过程，其协方差为θh=[ θh1， θh2，…，θhn]T为 高 斯过 程 zh(X )的 模 型超参数。空间相关函数R(X(i)，X(j)；θh)为超参数θh和qh以及高可信度训练样本Sh的函数。yc(X)的表达式为

其中：αci和Ac分别表示校正展开多项式项系数和相应的多项式项索引集合；ŷl(X)为低可信度多项式混沌-Kriging（PC-Kriging）模型预测器；zl(X )为低可信度PC-Kriging 模型yl(X)的静态高斯随机过程；ψi(X)和ψci(X)分别为yl(X)的多项式混沌项和矫正展开多项式混沌项；βi为低可信度多项式混沌项系数。多项式混沌矫正项集合Ac的势应该小于低可信度稀疏多项式集合A 的势，即Ac⊂A，其中A={i1，i2，…，iM}为低可信度PCKriging 模型yl(X)中多项式项索引集合。通过使用低可信度样本构建基于集合Ac的势应该小于低可信度稀疏多项式集合A 的势，即Ac⊂A。

通过使用基于最小角回归的留一交叉验证（Leave One Out Cross-Validation-based Least Angle Regression， LOOCV-LAR）自 适 应 基 函数选择方法得到M 个最重要的基函数后，再使用一般高斯过程回归分析可以得到低可信度PC-Kriging 预测器为[25］

式中：βij为基函数ψij(X)对应的系数；rl、Rl、Ψ以及β分别为低可信度PC-Kriging 模型中自相关函数向量、样本相关函数矩阵、多项式基函数矩阵以及多项式系数向量；Yl为低可信度响应向量。通过代入式（8）～式（10）得

其中：α0以及{αci}是需要被精确训练的缩放因子。子集Ac应该通过一个合适的标准进行选择。

本文利用LOOCV-LAR 算法选择最相关的稀疏多项式基函数作为PC-Kriging 模型的趋势函数，即PC-Kriging 模型中基函数已经按照重要性进行排序。越靠前的多项式项对输出贡献越大也最重要。因此，通过利用非常少的高可信度样本仅仅矫正排序靠前的多项式系数，就能获得对低可信度PC-Kriging 的有效矫正。为此，本文设计了一种新的基于LOOCV 的自适应基函数选择方法，即在选择最相关的M项低可信度多项式项之后，再选择最优的矫正展开项集 合{ψi1(X)，ψi2(X)，…，ψiMc(X) }(Mc≤M)，以建立最优的AMF-PCK 模型，这个算法被定义为基 于 嵌 套 LOOCV 的 LAR 算 法（Nested LOOCV-LAR），可参考图1 和文献[24］。其中图1 为自适应选择最相关的低可信度多项式集合和最优的矫正多项式集合图中：ML为候选低可信度多项式基函数项数；M*和M*c分别为选择的最优低可信度多项式项数和矫正多项式项数。

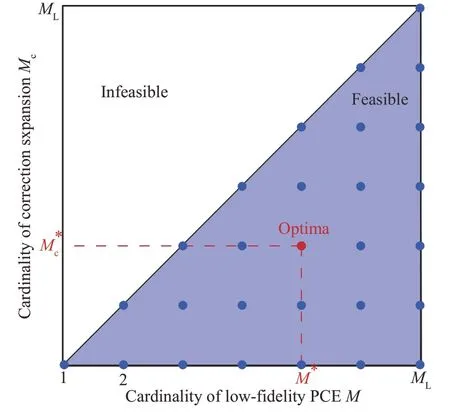
图1 自适应选择最相关的低可信度多项式集合和最优的矫正多项式集合Fig.1 Adaptive selection of the most relevant lowfidelity polynomial set and optimal correction polynomial set

在式（11）中的各项被确定后，通过标准Universal Kriging 拟合过程即可得到AMF-PCK 在未知点的预测模型。同Universal Kriging 模型一样，AMF-PCK 满足最小化均方误差和无偏估计假设（Best Linear Unbiased Predictor，BLUP）。AMF-PCK 预测模型在未知点X的预测值为

式中：Mc(Mc≤M)表示校正展开项中多项式项数量。

缩放因子以及校正展开多项式系数向量α=[α0，αc1，αc2，αcMc]T可通过广义最小 二乘方 法估计得到，即

式中：矩阵F中第1 列和其他列是通过顺序代入高可信度观测点集合Sh到(X)和ψci(X) (i=1，2，…，Mc)中计算得到。相关函数Rh中未知超参数θh和qh通过最大化似然函数得到。而AMF-PCK 预测模型在测试点X的估计均方误差（Mean-Squared Error， MSE）为

式（14）提供了一个非常有用的MSE 估计，同Kriging（或高斯过程）模型本身的优势一样，合理的MSE 估计能帮助AMF-PCK 代理模型自适应地修订预测精度以及有利于基于（多可信度）期望改进（Expected Improvement， EI）的全局优化。本文使用粒子群算法与基于梯度的稀疏非线性优化器（Sparse Nonlinear Optimizer， SNOPT）相结合，以得到全局最优的超参数θl、 ql、 θh和qh。其中θl、ql代表低可信度PC-Kriging 模型的超参数。优化过程中优化范围定义为[10-4θini，104θini]，θini是超参数初始值。首先使用粒子群优化算法搜索全部设计空间找出可能的全局最优所在区域，然后使用基于梯度的SNOPT 利用粒子群优化方法提供的初值进行第2次搜索直至收敛。

3 基于新型AMF-PCK 模型的多目标优化方法

3.1 非线性目标降维策略

以主成分分析（Principal Component Analysis， PCA）（ 本 征 正 交 分 解、奇 异 值 分 解、Karhunen-Loève 转换等）为代表的线性目标降维方法通过投影当前高维数据到相关矩阵的特征向量方向，以找到数据的本质结构或主方向。PCA移除了当前数据的二阶相关性。然而对于更加复杂的相关结构，如多峰高斯分布或非高斯分布等，PCA 难以找到最重要的主特征方向，使得降维失败。一些文献已经提到了类似问题[1，26］，并通过引入非线性降维途径试图解决，比如Correntropy-PCA（C-PCA）、最大方差展开（Maximum Variance Unfolding， MVU）等。本文引入基于MVU的非线性目标降维方法[27］，以处理一般的工程问题。MVU 学习高维数据的相似性，在映射前后保持与临近点局部欧式距离以及角度相等，进而能有效学习高维数据中的低维流形，反映流形的维数。MVU 可视为自动训练核矩阵K 的核主成分 分 析（Kernel Principal Component Analysis， KPCA）的一种，然而相对于KPCA，MVU 不包含待训练参数以及能保持映射前后的邻接关系不变。基于MVU 的目标降维算法为

1）首先通过经典的多目标进化算法（Multi-Objective Evolutionary Algorithms， MOEAs），如基于分解的多目标进化算法对高维问题进行优化搜索一些代数后得到近似Pareto 解集。假设每代种群数量为Np，目标个数为M，得到的搜索多目标结果集合为F=[ f1，f2，…，fNp]，其中列向量fi=[ fi1，fi2，…，fiM]T∈RM表示这一代第i 个粒子各个目标的适应值。

式中：ωij表示fi与fj是否是ϱ-近邻，如果是，则为1，否则为0。ϱ 代表最近邻居的个数，文献[28］指 出 ϱ 通 常 取 为近 邻 矩 阵Ω=首先通过输入数据计算得出。上述优化约束保证了高维空间数据映射到低维空间时近邻的欧式距离不变。上述优化问题通常非常耗时，且不容易得到最优解。通过学习KPCA 方法，引入核矩阵，则上述优化问题可转化为

上述凸半正定优化问题可通过SeDuMi[29］求解。如果使用PCA 线性降维，则可直接计算协方差矩阵为

3）对得到的核矩阵K 或者R 进行特征分解，即K=VΛVT。 其 中V 为 特 征 向 量 矩 阵V=[v1，v2，…，vM]，vi=[vi1，vi2，…，viM]T和相应的特征 值 Λ=diag(λ1，λ2，…，λM) (λ1≥λ2≥…≥λM≥0)。

5）定义降维后的初始目标集合F=∅，对于 第1 个 重 大 方 向vj(j=1，2，…，m)：① 如 果fi(i=1，2，…，M)目标对v1方向的贡献中存在符号相反的一些，则选择最正和最负贡献对应的2 个目标进入集合F；② 如果fi(i=1，2，…，M)目标对vj(j≥2)方向的贡献中存在符号相反的一些，记最正贡献为vpj以及最负贡献为vnj，如果|vnj|≥vpj≥θt|vnj|则 选 择vpj和vnj对 应 的2 个 方 向均进入F，如果vpj＜θt|vnj|则选择vnj对应的方向进入F，如果vpj≥|vnj|≥θtvpj则选择vpj和vnj对应的2 个方向均进入F，如果|vnj|＜θtvpj则选择vpj对应的方向进入F，本文取系数θt=0.8；③ 如果所有fi(i=1，2，…，M)对vj方向的贡献符号相同，则选择贡献最大的2 个目标进入集合F，F 应该满足F ⊆F，记mv=Card(F )。

6）使用相关性分析对F 中的相关目标（贡献等同的）进一步识别和缩减。将入选F 中的目标按列按顺序放在矩阵H 中，然后计算相关矩阵R=HHT/M。对于fi∈F 以及fj∈F，如果满足sign(Rik)=sign(Rjk) (k=1，2，…，M)以及Rij≥Rθ，则说明fi与fj的贡献方向相同，则选择其中对主导方向贡献更大的一个，即如果ci≥cj则选择fi，从F 中 剔 除fj，反 之 亦 然。其 中Rij表示R的 元素。Rθ的选择与目标间的冗余度有关，目标越冗余Rθ越大，反之越小。文献[28］使用Rθ=1.0-e1(1.0-M0.954/M)，其中M0.954指前M0.954个主成分占据了0.954 的总能量。

7）用新得到的集合F 替换旧集合F，重复步骤2～步骤6 直到连续2 次得到的集合F 一样，则停止迭代，输出降维目标集合F*。

8）使用MOEAs 算法对新目标集合F*选择的目标进行搜索，得到Pareto 最优解集合，折衷选择最合适的设计，进行评估分析。

3.2 变可信度伪期望改进矩阵并行样本填充方法

在外循环中，每次多目标优化迭代结束后，需要选择新的样本填充点。设计变量作为优化粒子在不断进化，新样本的设计变量值X应该平衡全局探索与局部搜索的计算花费，如多目标期望改进（EI）准则，即多目标高效全局优化（Efficieng Global Optimization， EGO）。同时，每次迭代中，为了提高多可信度AMF-PCK 模型在特定空间内的预测精度，新加点的可信度水平也需要同时被确定。多目标EGO 准则虽然从很早开始已经获得了广泛研究，比如基于欧式距离改进的EI准则[30］，基于最大最小距离改进的EI[31］，基于超体积改进的EI[32］，基于切比雪夫度量改进的EI[33］等。然而，这些方法应用到高维多目标(m≥3)加点时，多目标EI的计算是一个典型的高维积分问题，计算花费随目标个数增多剧烈增加。并且其每次只能添加1个样本，面对高维多目标问题(m≥3)时，其有效性仍待验证[34］。Keane[30］提出使用蒙特卡洛模拟（MCS）近似高维积分，计算准确性与所使用样本数密切相关，其计算花费仍然难以承担。Singh 等[15］提出了一种快速计算基于超体积改进EI和基于欧式距离改进EI的方法，在较低维度时，其计算花费有明显降低。因此，针对以上问题，提出了一种变可信度伪期望改进矩阵（Variable-Fidelity Pseudo Expected Improvement Matrix， VF-PEIM）并行样本填充方法。期望改进矩阵（Expected Improvement Matrix， EIM）标 准 是 由Zhan 等[34］提 出 的一种高效多目标EI 填充方法，其通过将上述传统的多目标高维EI函数积分问题转化为多个一维EI积分之和，每个EI函数即EIji代表针对第j个Pareto前缘点，第i个目标的期望改进。二维EIM 如图2所示。本文提出使用VF-EI定义EIji为

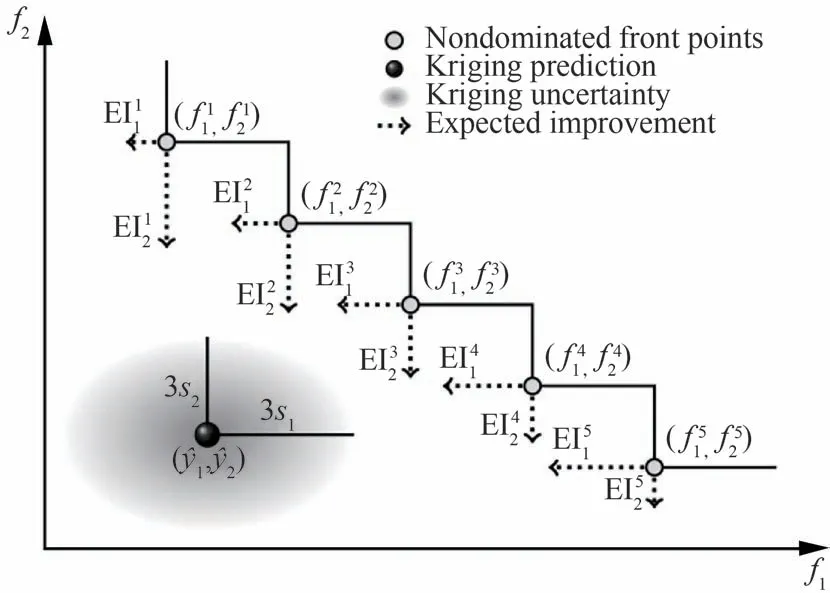
图2 二维EIMFig.2 Two-dimensional expected improvement matrix

式中：l 代表可信度水平。在定义了式（17）后，可将欧式距离改进准则[30］中的高维积分问题转化为多个一维积分求和，即

通过对式（19）单目标优化搜索可获得1 个最有潜力改进点位置，即

然而，式（20）每次只能添加1 个样本点，这对于多目标优化问题通常是非常低效的。为此，引入伪期望改进矩阵（Pseudo Expected Improvement Matrix， PEIM）填充准则[35］，在每个加点阶段，通过迭代优化选取若干个样本点。其中，第1 个加点位置通过式（20）得到，记为{ X1，l1}。然后，计算PEI 准则为

第Nc个样本点位置为

式（21）～式（24）的优化均是单目标优化问题，因而相对多目标优化效率很高。VF-PEIM 通过定义每个修订周期合适的加点数，即可有效地获得全局最优解，从而兼顾了多目标优化效率和搜索能力。

3.3 高维多目标优化框架

针对式（4）的多目标稳健优化设计模型，每个目标在进化迭代过程中均需要进行稳健性σfi(X)和平均表现μfi(X)评估，这通常是非常耗时的。同时，因为有的目标通常在不同的设计状态（针对同一设计状态的阻力值和力矩值只需要1 次评估，而不同状态下的阻力值则需要分别评估），也许会卷入不同的不确定因素，因此会包含多个样本设计，即需要建立针对多个目标和约束的多个代理模型。为此，本文基于AMF-PCK 模型建立同时考虑设计变量与随机变量的联合代理模型。利用3.1 节引入的非线性目标降维策略[36］，建立了针对复杂工程优化问题的高维多目标稳健优化框架，其流程如图3 所示。其包含4 个主要步骤：① 针对式（4）的优化模型定义设计变量和随机变量，通过有效的抽样方法获取一定的样本并评估其表现，建立针对不同目标的代理模型；② 使用MOEA/D 多目标优化算法对初始包含多个目标的设计问题进行优化设计，并获得收敛解；③ 使用降维方法对多目标进行降维分析，获得降维后的目标集合；③ 对降维后的目标集合进行重新优化搜索，获得收敛解；④ 分析Pareto 解，并利用提出的变可信度伪期望改进矩阵（VFPEIM）并行样本填充策略填充新的样本，构建新的代理模型，重复步骤②～步骤④，直到收敛。

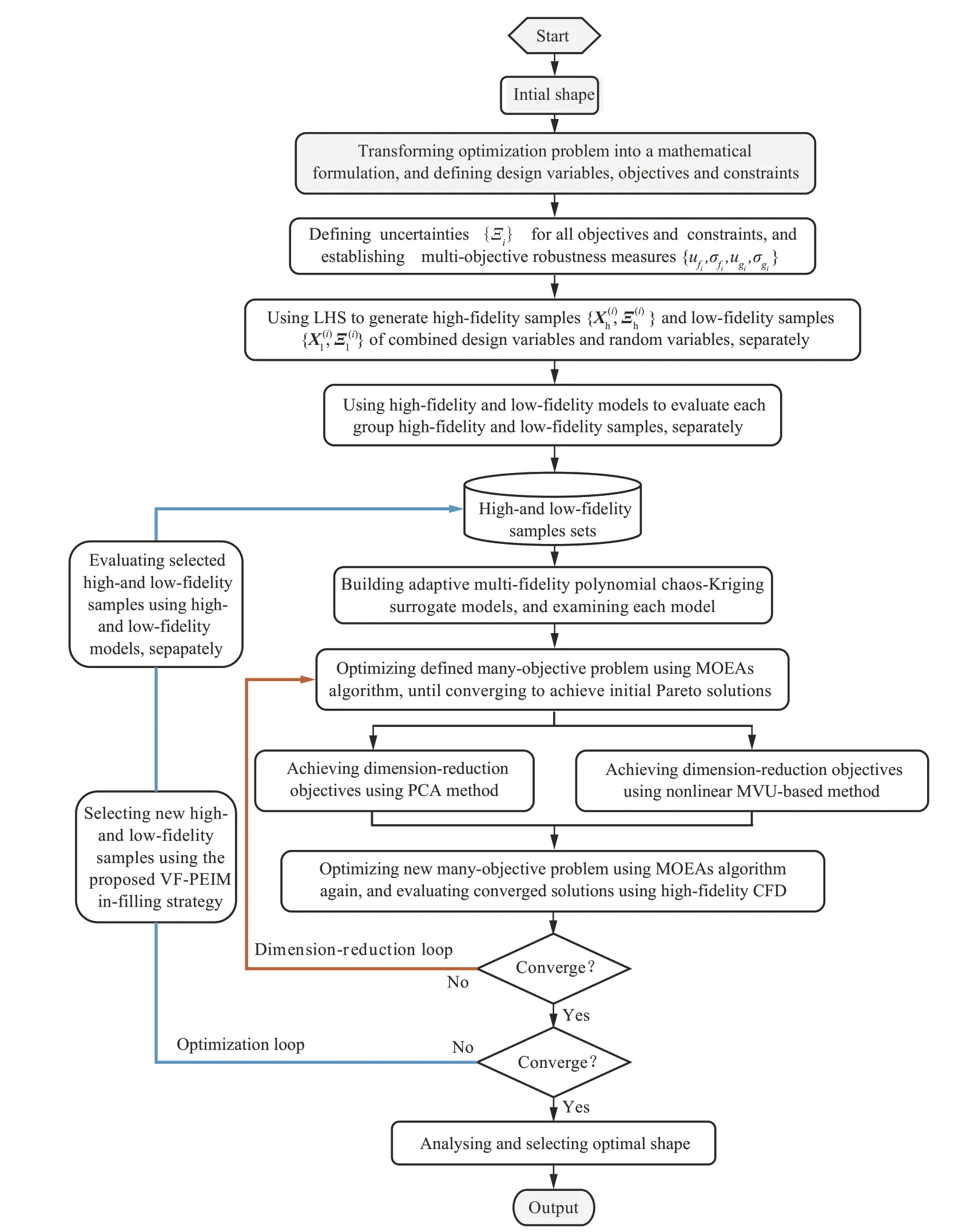
图3 基于AMF-PCK 的多目标优化流程Fig.3 Many-objective optimization flow chart based on AMF-PCK

3.4 数值算例测试

采用经典的DTLZ5 函数测试所提出方法的优化效果，具体函数表达式可参考文献[1，26］。测试算例均使用2 层可信度函数构建AMF-PCK 代理模型，即l=1。多目标优化算法均使用基于分解的多目标进化算法即MOEA/D，均使用基于惩罚的边界交叉（Penalty-based boundary Intersection， PBI）聚合方法，邻居个数均为20，粒子数均为300，进化代数均为500。在并行加点子优化中，均使用单目标加强学习粒子群优化（Comprehensive Learning Particle Swarm Optimizer， CLPSO）算法搜索新的加点位置。针对VF-PEIM 方法，使用拉丁超立方抽样（LHS）方法在设计空间[0，1]D内产生3D个初始高可信度样本以及40D个初始低可信度样本，D为设计变量个数。而针对PEIM 方法，使用Kriging 模型进行代理以及使用LHS 方法选择10D个高可信度点作为初始样本。选择转世代距离（Generational Distance， GD）和反转世代距离（Inverted Generational Distance， IGD）指标评价2 种方法得到的非支配解集的收敛性和分布性，其中参考解是在真实的Pareto前缘上均匀地选取10 000个离散点得到。

图4 为使用基于PEIM 和VF-PEIM 加点优化方法分别执行。在10 次迭代后，结果对比如图4 （a）所示，基于AMF-PCK 代理模型的VFPEIM 加点方法在同样的迭代次数下获得更低的IGD 值，即Pareto 解集更好的均匀性和收敛性。并且基于VF-PEIM 方法到10 次迭代时，IGD 值已经基本收敛，而PEIM 方法收敛较慢。比如在10 次迭代后，针对3 目标DTLZ5 函数，PEIM 加点方法得到的IGD 值为0.047 104，而基于VFPEIM 方法得到的IGD 值为0.020 379。可见，相对于经典PEIM 策略，提出的VF-PEIM 加点策略优化效果和效率得到显著改善。在10 次迭代后，2 种方法收敛的Pareto 解集与真实Pareto 解集对比如图4（b）所示。可以看出，相对于经典的PEIM方法，基于VF-PEIM 方法获得了与真实Pareto 解更贴近和分布范围更广的解集。原因之一在于，在相同迭代次数下，AMF-PCK 能提供更准确的预测精度，因而MOEA/D 方法能有效地搜索最优Pareto 解集。结果验证了基于AMF-PCK 的VFPEIM 并行加点优化方法的有效性和可靠性。

图4 使用基于PEIM 和VF-PEIM 加点优化方法分别执行10 次迭代IGD 和得到的Pareto 解集对比（DTLZ5 函数）Fig.4 Comparison of IGD and Pareto solution set using infilling-based PEIM and VF-PEIM methods respectively based on 10 iterations （DTLZ5 function）

为了进一步验证提出的方法在更多目标优化问题中的适应性，使用目标个数M={3，4，5，6，7，8，9，10 }的DTLZ5 函 数 进 行 分 析。基于PEIM 和VF-PEIM 的2 种方法所有设置同上，均执行10 次加点迭代。基于PEIM 和VFPEIM 这2 种方法得到的结果对比如表1 所示。从表1 可以看出，随着目标个数增加，基于PEIM和VF-PEIM 加点优化方法得到的GD 和IGD 值在M≥5 后均迅速增加，即Pareto 解集的收敛性和均匀性迅速变差。基于VF-PEIM 的加点优化方法表现要优于基于PEIM 加点优化方法，即各个目标下更低的GD 和IGD 值。

为了解决目标个数M≥5 后收敛性和多样性迅速变差的问题，在迭代优化过程中引入基于MVU 的非线性目标降维策略，详细过程如3.1 节所述，记为VF-PEIM- MVU 方法。该方法先使用基于VF-PEIM 加点优化方法收敛后，对得到的高维多目标（M≥5）Pareto 解集使用目标降维方法筛掉冗余目标，然后对降维后的目标集合使用基于VE-PEIM 加点优化方法进行再次优化。如图3 所示执行迭代优化直至降维目标集合和Pareto 解集收敛。从表1 可以看出，基于VFPEIM-MUV 方法在高维多目标优化问题下得到的Pareto 解集GD 和IGD 指标均有所改善，即Pareto 解集具有更好的收敛性和分布性，并明显好于基于VF-PEIM 和PEIM 优化加点方法得到的结果。从而验证了提出的方法在高维多目标优化问题中的适应性和有效性，以及其相对于经典的PEIM 多目标加点优化方法产生的显著改进。

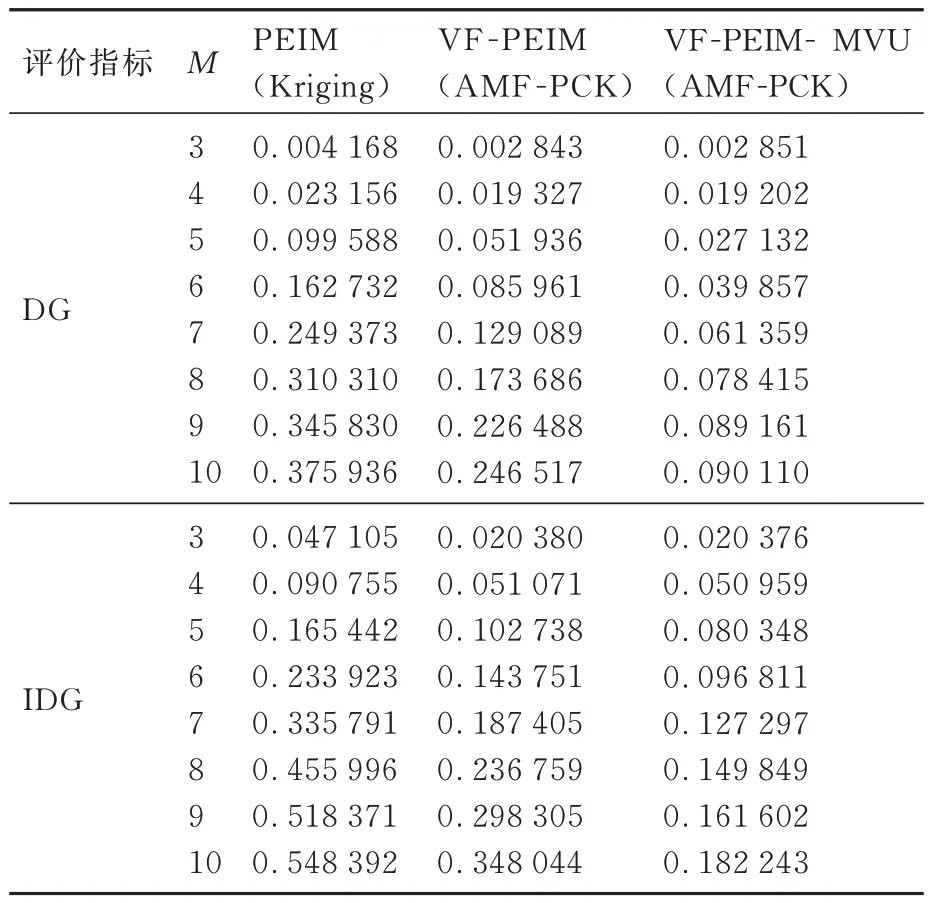
表1 不同代理优化算法的Pareto 解集的评价指标对比（DTLZ5 函数）Table 1 Comparison of evaluation indexes for Pareto solution set of different surrogate-based optimization algorithms （DTLZ5 function）

从图3 也可以看出，相对于PEIM 和VFPEIM 方法，VF-PEIM-MVU 方法多了降维分析-多目标再次优化循环过程，可能带来额外的计算花费。但实际上由于降维分析过程非常快，而且基于降维后的目标再次进行多目标优化的计算花费显著低于高维多目标直接优化，因而图3 所示的过程多出来的这一步（降维分析-多目标再次优化）并不会带来计算花费的显著增加，反而加速了整个高维多目标优化问题的收敛，以及缩短了搜索到相同Pareto 解集所需要的时间。

4 高速旋翼翼型高维多目标优化设计

7%厚度旋翼翼型位于桨叶桨尖剖面，前飞时前行马赫数非常高，激波强度和激波位置随马赫数变化非常敏感。据此，建立了考虑高速马赫数不确定性的多目标稳健优化模型，即

式中：μ((Ma))和σ((Ma))分别代表马赫数Ma服从均匀分布U( )0.85， 8.87 ，升 力 系 数Cl=0 时的均值和方差；ω1和ω2为强调性能表现和稳健性的权值，ω1越大则越强调性能表现，ω2越大则越强调稳健性，反之亦然；t和t0分别代表候选翼型最大厚度和最大厚度约束值，本文中取t0=7%；Re和Alpha 分别为流场雷诺数和翼型迎角。高速旋翼翼型要求尽可能低的俯仰力矩系数，以降低配平阻力。因此本文在式（25）中将一段范围内（Ma∈[0.85， 8.87]）的力矩系数绝对值最大值作为目标进行设计分析，以研究力矩系数与阻力系数等其他气动特性的相关性，为寻找最优的多目标稳健设计翼型提供参考[37-38］。

基于图3所示优化流程，首先采用LHS抽样方法在设计空间内产生4n个初始高可信度样本以及50n个初始低可信度样本，n为设计变量数目。计算分析方法采用验证的基于剪切应力输运（Shear Stress Transfer， SST）的数值转捩模拟程序，计算雷诺数为Re=Ma×7.2×106，来流湍流度为0.5%。参数化方法为类函数/形函数（CST）方法，设计变量为d=24 个。依然采用第2 节提出的层流翼型网格生成方法分别生成不同网格量的数值网格，其中高、低可信度计算使用的网格量分别为126 360 和19 200。2 种网格近场分布如图5 所示，x和z分别为翼型在流场中沿来流和垂直于来流方向的坐标，c为弦长。

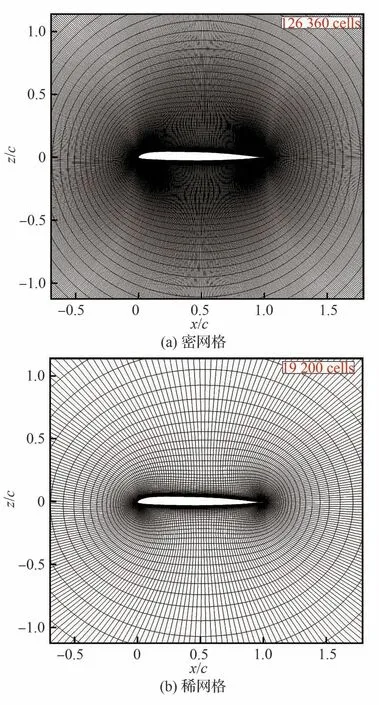
图5 高、低可信度CFD 数值模拟所使用的密网格和稀网格近场分布Fig.5 Distributions of fine and coarse grids used in highfidelity and low-fidelity CFD simulation

对这7 个目标使用基于分解的多目标进化（MOEA/D）算法的VF-PEIM 并行加点准则进行优化。MOEA/D 算法使用边界交叉聚合方法，邻居个数为20，粒子数为2 100，进化代数为800。在加点子优化中，均使用单目标加强学习粒子群（CLPSO）算法搜索新的加点位置，粒子数为设计变量个数，算法停止标准为连续搜索到的加点距离变化小于10-8。其中每个子迭代中基于优化的Pareto 解均选择10 个新的高可信度样本点添加到样本库中，即Nc=10 后停止子优化过程。加点优化迭代50次后，进行评估获得476个初步收敛的非支配解。详细流程如图3所示。对获得的收敛解通过3.1 节陈述的降维方法进行目标降维分析，获得核矩阵K∈R7×7的特征值和特征向量。对特征值按照降序的顺序进行排列，如表2 所示。可以发现特征值从e1到e7迅速衰减。本文按照θ=95%能量贡献准则进行截断选择，保留前3 个重大特征值及主特征向量，其中对应于前3 个特征值的主特征向量（列向量）按顺序被放在表3，即V1～V3。在表格中，第1个列向量即最重要的主特征向量V1中第1个元素和第5 个元素分别为最负和最正的元素，其对应的第1个和第5个最矛盾的目标，且对主特征向量贡献最大，因此第1个和第5个目标进入降维目标集合F={f1，f5}。第1个目标优化高速阻力及阻力发散特性，要求翼型具有更低的弯度和靠后的最大厚度位置，而第5个目标提高低速升力及升阻比特性，要求翼型具有更大的弯度以及更大的前缘半径，因此其存在天然的矛盾。在第2个主特征向量V2中，第4个元素vp2和第6个元素vn2为分别为最正和最负的值，且满足|vn2|＜0.8vp2，因此选择vp2对应的目标f4进入目标集合F={f1，f5，f4}。在第3 个主特征向量V3中，第2个元素vn3和第6个元素vp3分别对应最负和最正的值，且满足vp3＜0.8|vn3|，因此选择vn3对应的目标f2进入目标集合F={f1，f5，f4，f2}。至此，通过降维分析成功选取了4个目标进入降维目标集合，略去了3个冗余目标。

表2 核矩阵特征值Table 2 Eigenvalues of kernel matrix

在获得以上降维目标集合F 后，对降维目标集合F 中的目标对应的目标向量H={f1，f5，f4，f2}进行相关性分析，计算目标相关矩阵R。从表3 中可以看出这4 个目标贡献方向互不相同，其中Rθ=0.639 916，因此不再剔除任何目标，如表4 所示。通过对这4 个目标分析可以发现，第2 个目标为力矩特性要求，第5 个目标为降低中等升力系数下的阻力即提高其升阻比，在无激波状态下其优化潜力很小。因此通过将第2、第5 个目标，以及冗余目标变为约束，使原始7 目标优化问题转化为如下双目标优化模型：

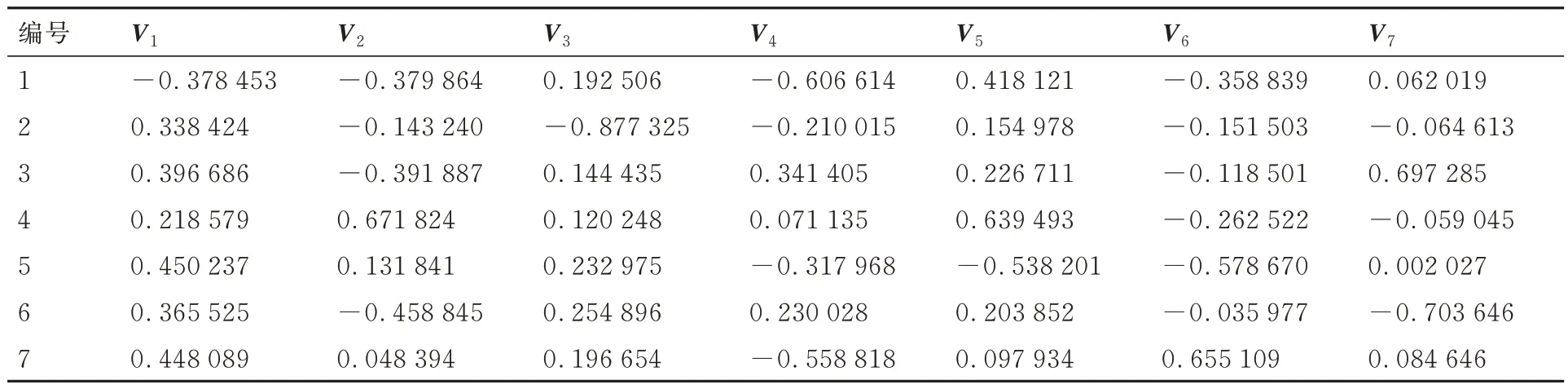
表3 对应于特征值顺序的特征向量（列向量）Table 3 Eigenvectors （column vector） for corresponding eigenvalues

表4 降维后目标相关性分析Table 4 Correlation analysis of reduced objectives

式中：μ((Ma))和σ((Ma))分别代表马赫数Ma服从均匀分布U( )0.85， 8.87 ，升力系数Cl=0 时的均值和方差；ω1和ω2为强调性能表现和稳健性的权值参数，ω1越大则越强调性能表现，ω2越大则越强调稳健性，反之亦然；ω3为第2 个目标的权值系数；t和t0分别代表候选翼型最大厚度和最大厚度约束值，本文中取t0=7%。Cd0、Cd1、Cd2和Cd3分 别 代 表原 始 翼 型 在 设 计 状态：①Ma=0.6，Cl=0.6，Alpha=4o；②Ma=0.5，Cl=0.6，Alpha=5o； ③Ma=0.4，Cl=0.9，Alpha=8o；④Ma=0.5，Cl=0.8，Alpha=6o下的阻力系数，而Cm0代表原始翼型在Ma∈[0.85， 8.87]范围内，Cl=0 时最大力矩系数的绝对值。通过将这5 个非主要冲突目标转变为有效约束，可有效缩减翼型设计空间和引导搜索方向，进而提升多目标优化效率。

对以上两目标优化问题，目前许多流行的多目标优化算法均能取得良好的优化效果。首先由LHS 方法产生4d个初始高可信度样本以及50d个初始低可信度样本，构建AMF-PCK 代理模型。其中d为设计变量个数。本文使用经典的MOEA/D 算法进行优化搜索，种群大小为200 并更新1 000 代，在每次搜索结束后采用提出的VF-PEIM 并行样本填充策略选择Nc=5 个新的高可信度样本到样本库中。高、低可信度CFD 数值分析所使用的计算网格近场分布如图5 所示。迭代60 次后收敛，进行评估得到1 组收敛的Pareto 解 集，如 图6 所 示，目 标1（Obj1）和 目 标2（Obj2）。图7 给出了多目标加点优化过程中每次搜索完成加点时预测平均阻力系数绝对误差（Absolute Error）随迭代次数（Iteration Number）的变化。可以看出，阻力系数预测误差从最初的接近10×10-4（10 counts）到第40 次迭代时已经小于2 counts，代理模型预测精度基本收敛。

图6 多目标优化得到的Pareto 前缘Fig.6 Pareto solutions obtained from multi-objective optimization

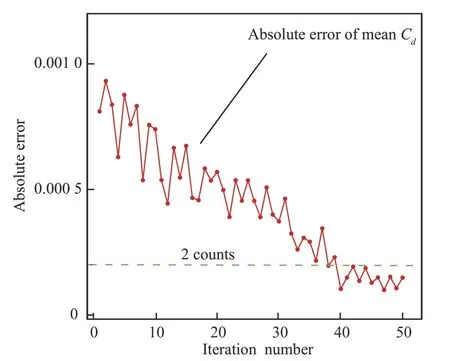
图7 优化过程中阻力均值绝对误差Fig.7 Absolute errors of mean values of drag coefficients in optimization process

为了比较优化效果，从收敛的Pareto 前缘中选择3个有代表性的翼型进行对比，如图8所示，分别 记 为OPT0701、OPT0702 和OPT0703 翼 型。其中OPT0701 翼型是一种高速与低速特性比较均衡的外形。而OPT0702 和OPT0703 翼型更侧重于高速特性，降低高速下的激波阻力并集中提高阻力发散马赫数，以满足高速旋翼翼型特殊设计需求。选择的3 个翼型外形和经典的OA407 外形对比如图8 所示。可以看出，优化的3 个翼型相对于OA407，弯度均有所降低，其中OPT0702 和OPT0703 弯度下降较多。OPT0701 相对于OA407 前缘半径略有减少，最大相对厚度位置后移。OPT0702翼型前缘半径以及前缘厚度相对于OPT0703 翼型变大，而OPT0703 翼型最大相对厚度位置相对于OPT0703和OA407均后移。

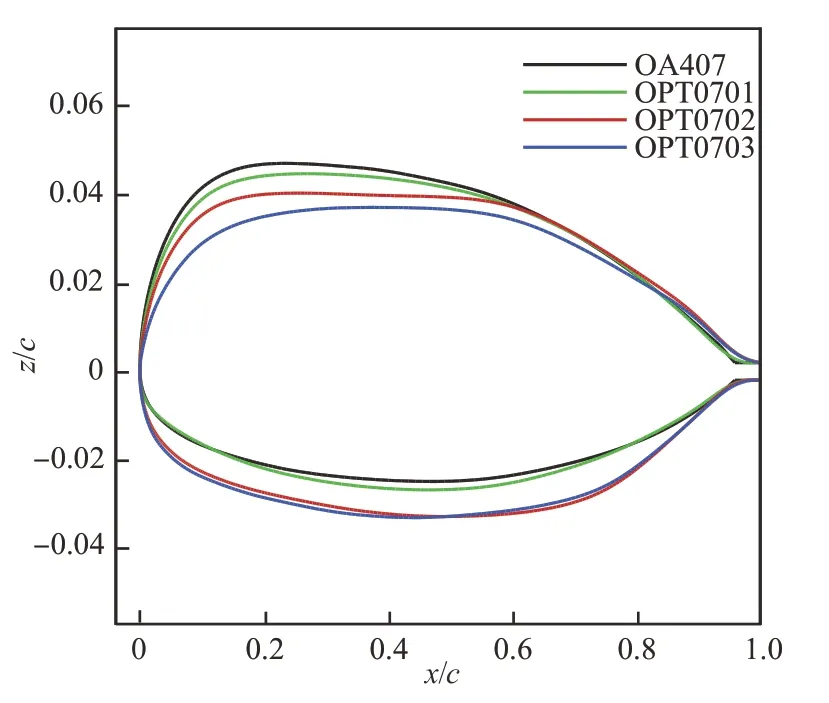
图8 优化翼型与对比翼型外形对比Fig.8 Comparison between optimized airfoils and comparative airfoil

图9给出了零升状态4个翼型压力分布（Cp）曲线对比。OA407 上下表面均出现一道强激波，而OPT0701、OPT0702 以及OPT0703 翼型上表面均由双弱激波代替，并且其下表面也出现了比OA407 更弱的一道激波。尤其OPT0703 翼型在上下表面的激波强度均要弱于OPT0702 和OPT0701翼型。零升阻力发散特性曲线如图10所示，Cm表示俯仰力矩系数。OPT0701、OPT0702和OPT0703 翼型阻力发散马赫数分别为0.861、0.869 和0.875，相对于OA407 翼型的0.854 阻力发散马赫数，设计翼型阻力发散马赫数分别提高了0.007、0.015 和 0.021。 并 且 OPT0702 和OPT0703 翼型零升阻力系数也显著低于OA407翼型。在Ma=0.87 下，3 个设计翼型相对于OA407翼型阻力系数均降低超过20 counts。力矩特性曲线显示设计翼型OPT0702 和OPT0703 力矩系数绝对值在马赫数0.80～0.87 范围内均小于0.02，并明显好于OA407 翼型的力矩特性，而OA407翼型力矩特性随阻力发散后急剧变差。

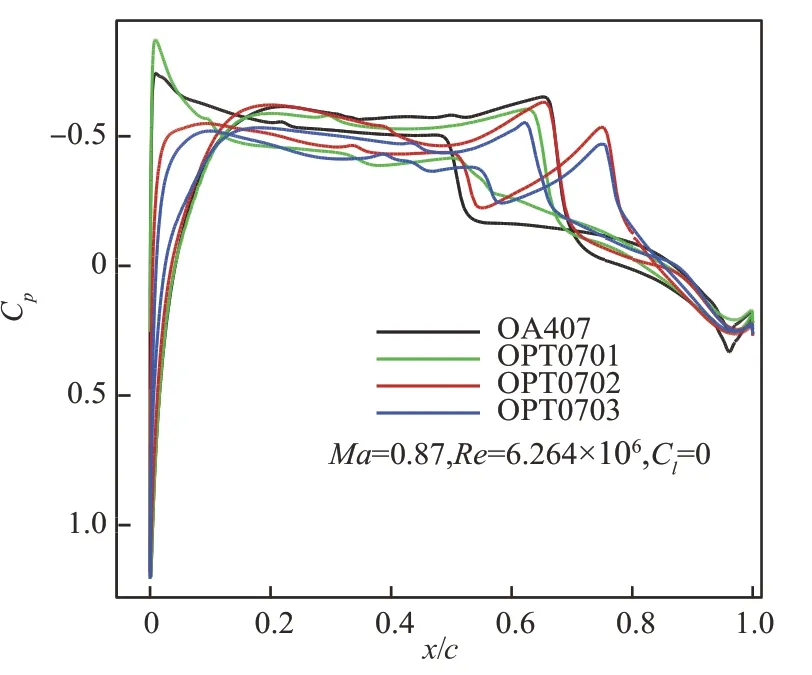
图9 零升状态压力分布对比Fig.9 Comparison of pressure distributions at Cl=0

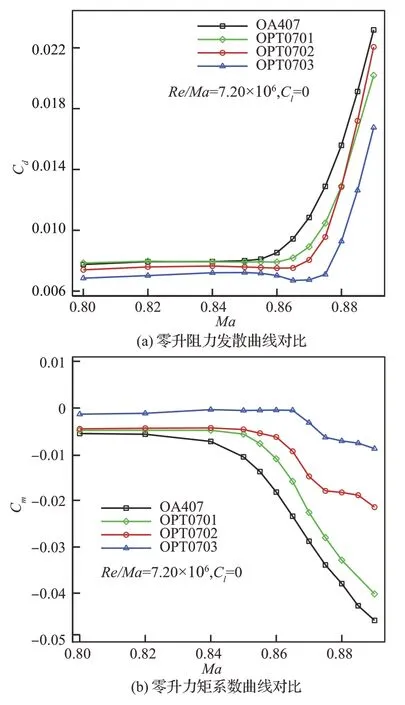
图10 气动力特性曲线对比Fig.10 Comparison of aerodynamic characteristics curves

7%厚度翼型位于桨叶尖部，（共轴双旋翼直升机）高速前转时马赫数超过0.87，上下表面均非常容易出现强激波，因此提高其阻力发散马赫数以及降低基础阻力对减少飞行阻力具有重要价值。同时在机动以及悬停时，巡航马赫数降低，为了配合桨叶其他部分产生收益，希望其能提供较大的最大升力系数以及一定的升阻比。当然，由于其位于桨尖部分较小的一段，因此其所能提供的载荷也非常有限。图11～图14 分别给出了设计翼型与OA407 翼型在Ma=0.3、Ma=0.4、Ma=0.5、Ma=0.6 下升力系数（Cl）随迎角（Alpha）变化曲线，以及升阻比（K）随升力系数（Cl）变化曲线对比。可以看出，设计的OPT0701翼型在Ma=0.3～0.6 范围内相比于OA407 翼型最大升力系数和最大升阻比均有不同程度提高。2 个高速翼型OPT0702 和OPT0703 在Ma=0.3～0.4 下升力特性和升阻比均相对于OA407有所降低，其中OPT0703 翼型相对于OPT0702翼型低速最大升力系数要低。到Ma=0.5～0.6时，OPT0702 翼型升力和升阻比特性基本与OA407 相 当，OPT0703 翼 型 在Ma=0.6 下 也 提供了和OA407 翼型接近的升力和升阻比特性。因为要协调旋翼翼型的多个气动特性，提高翼型高速阻力发散特性，翼型弯度降低，最大厚度位置后移，其低速特性（包括最大升力系数和最大升阻比）将会有所损失。并且为了维持稳健的高速阻力发散特性，使得OPT0702 和OPT0703 翼型上表面较为平坦，大迎角时非常容易出现强激波或者分离流，导致阻力增加。综合来看，OPT0701 翼型较OA407 翼型气动特性得到全面提升，包括高、低速特性，但高速特性提升有限；而OPT0703 翼型更强调高速特性，低速特性损失较大；OPT0702 翼型在保持一定高速特性的同时，低速特性损失较小。可见设计翼型要维持良好的低速特性（不差于OA407 翼型），高速特性将难以显著提高，进而难以满足高速直升机特殊的设计需求。

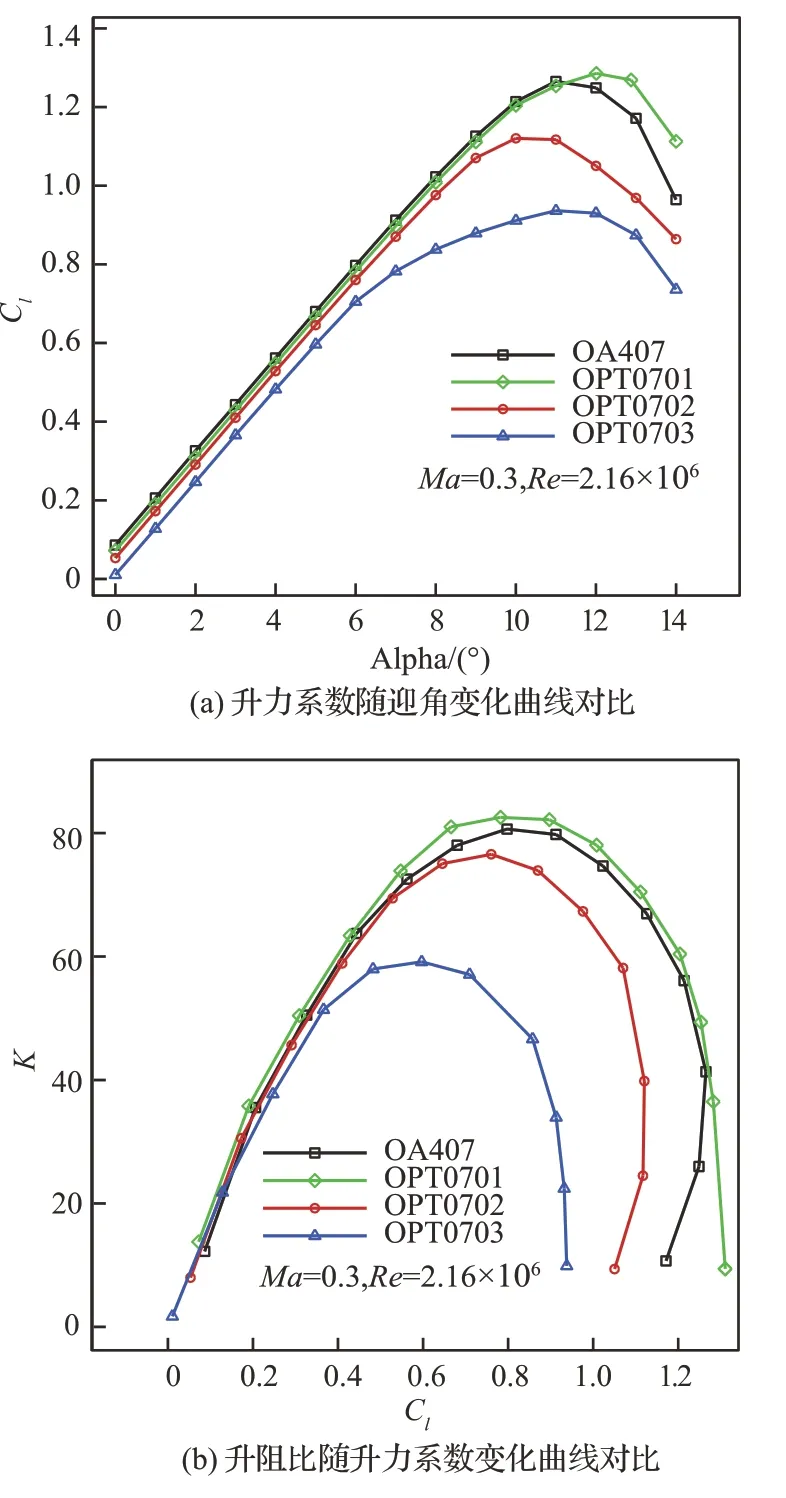
图11 Ma=0.3 下气动特性曲线对比Fig.11 Comparison of aerodynamic characteristics curves at Ma=0.3

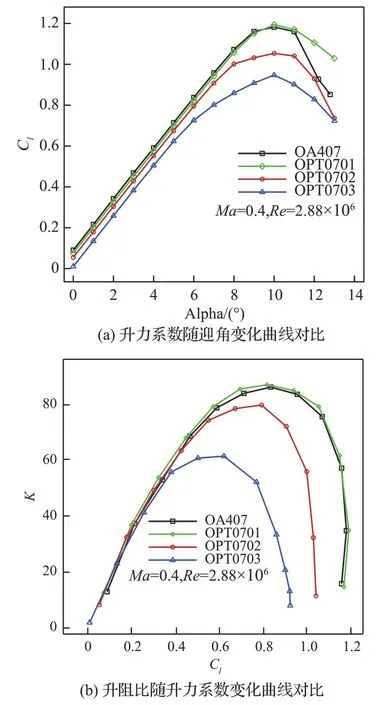
图12 Ma=0.4 下气动特性曲线对比Fig.12 Comparison of aerodynamic characteristics curves at Ma=0.4

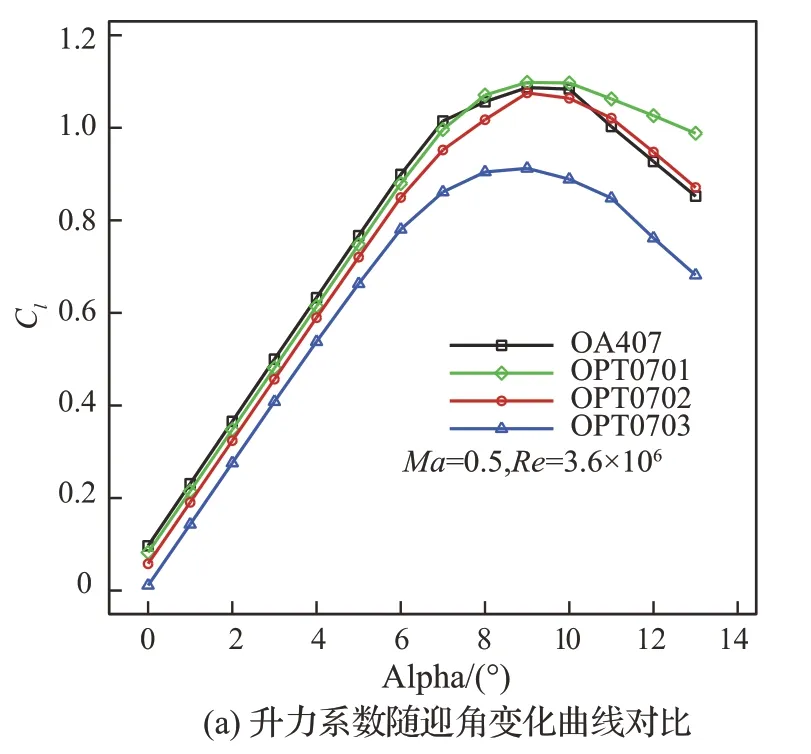
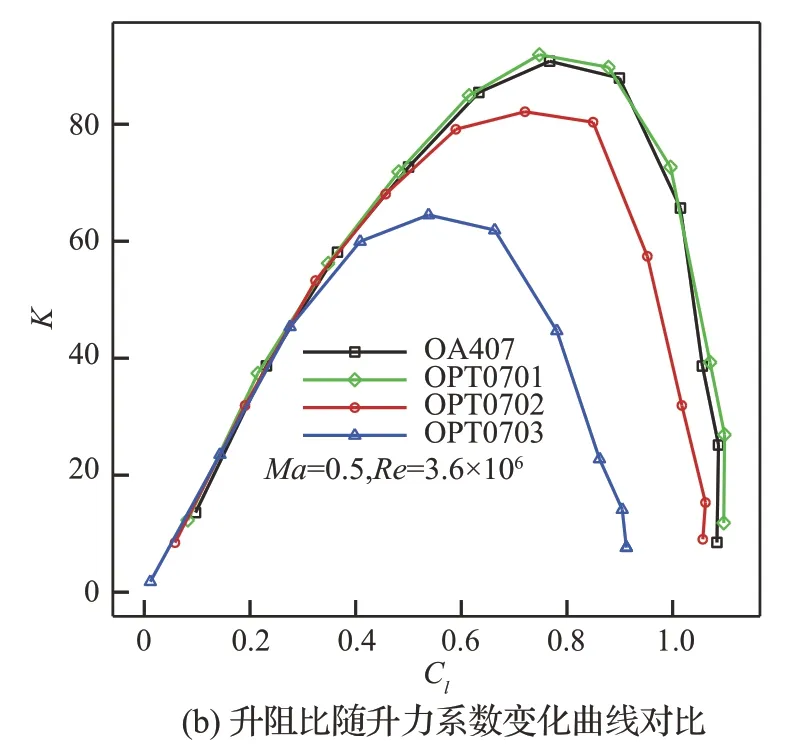
图13 Ma=0.5 下气动特性曲线对比Fig.13 Comparison of aerodynamic characteristics curves at Ma=0.5

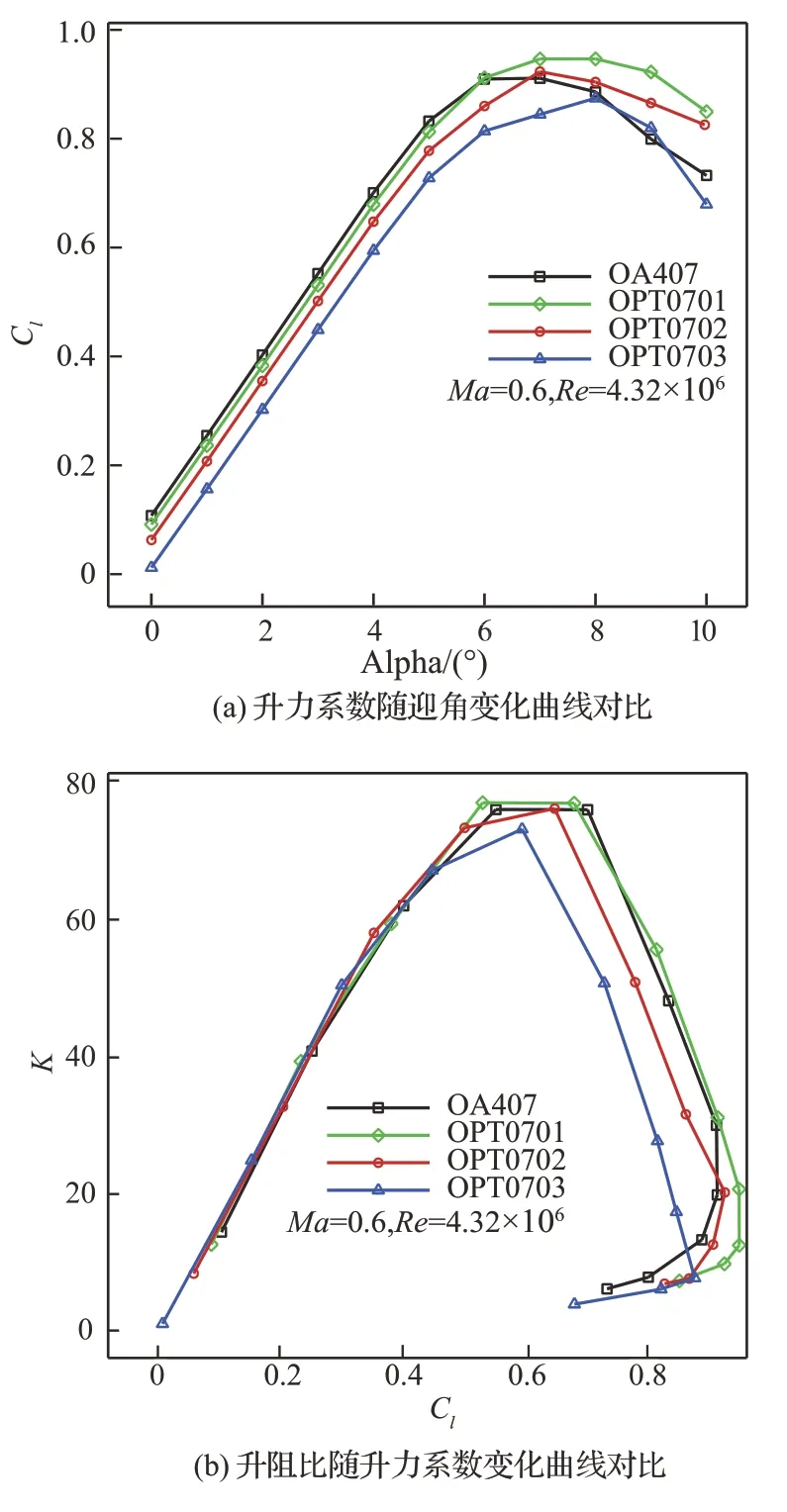
图14 Ma=0.6 下气动特性曲线对比Fig.14 Comparison of aerodynamic characteristics curves at Ma=0.6

高速直升机桨尖翼型几乎不承担载荷，设计翼型OPT0702 和OPT0703 的主要目的在于提高阻力发散马赫数和减小激波阻力，以满足桨尖翼型设计需求。结果也表明，此类翼型高速阻力发散特性与Ma=0.3～0.4 下升力特性矛盾性要强于Ma=0.5～0.6 下升力特性，这与上述目标降维分析结果一致。一些典型的气动特性对比如表5 所示。其中：Madd0表示零升阻力发散马赫数；Cd0表示零升阻力系数；Cm0表示零升力矩系数；Clmax表示最大升力系数；Kmax表示最大升阻比。可以看出，OPT0701 翼型所有指标均较OA407 翼型有不同程度提高，而OPT0702 和OPT0703 翼 型 均 相 对 于OA407 翼型高速特性指标提升明显，而低速特性指标有所损失。

表5 7%厚度翼型气动特性对比Table 5 Aerodynamic characteristics of 7% airfoils

5 结 论

随着刚性共轴双旋翼直升机飞行速度的提升，对高速旋翼翼型提出了更高的要求，包括更高的零升阻力发散马赫数和更低的基础零升阻力，中等速度高升阻比，低速高升力特性以及所有状态下更好的力矩特性，由此引发了高维多目标和复杂约束优化的难题。

本文针对这一难题，建立了多目标稳健优化方法，并发展了有效的多目标降维策略，以获得满足指标要求的最优解。同时建立了基于多可信度代理模型AMF-PCK 的高效多目标稳健优化方法，以及多目标优化加点方法使设计效率进一步提高。利用所建立的高效多目标稳健优化方法对7%厚度高速旋翼翼型进行了优化设计，设计翼型的气动表现与经典的OA407 翼型在高、中、低马赫数下进行了全面比较。

结果表明，相对于经典的OA407 翼型，设计的OPT0701 翼型较OA407 翼型高、中、低速气动特性指标全面提升，但高速特性提升非常有限；而OPT0702 和OPT0703 翼型在低速特性损失不大的情况下，高速特性提升显著且更加稳健。3 个设计翼型所有状态下的力矩特性也均好于OA407 翼型。设计结果再次说明了旋翼翼型各个目标特性强烈的矛盾性。考虑到刚性共轴双旋翼直升机翼型特殊的设计要求，设计翼型相对于经典的OA 系列翼型展示了显著的优势。设计结果验证了提出的高维多目标优化方法的有效性和可靠性。