光滑神经网络解决一类线性约束的非Lipschitz优化问题

喻 昕,舒浩帆,林植良,黄晓燕

(广西大学 计算机与电子信息学院,南宁 530004)(广西多媒体通信与网络技术重点实验室,南宁 530004) E-mail：enigma_hf@qq.com

1 引 言

近年来,在科学研究和工程应用中使用神经网络解决带约束的优化问题受到诸多学者的关注.1986年,Tank和Hopfield[1]提出了Hopfield神经网络用于解决线性规划问题,这启发了许多研究者使用神经网络的思想去解决优化问题.1988年,Kennedy和Chua[2]提出一种解决非线性规划的神经网络,该网络能够通过硬件实现从而解决实时问题.随后为了解决非光滑优化问题,Forti在文献[3]中,基于微分包含的思想,提出了一种使用了次梯度方法的神经网络解决非光滑凸优化问题.随着优化理论发展和深入,非凸优化的重要性逐渐得到重视.Liu[4]等人为了解决带盒约束和线性等式约束的非光滑伪凸问题,设计了一种使用罚函数方法的递归神经网络,Hu和Wang在文献[5]中提出一种解决不等式约束伪凸优化问题的投影神经网络,但这两种方法的有效性依赖于精确的罚因子.为了避免计算精确的罚因子,文献[6-8]分别提出不需要罚因子的神经网络来解决优化问题.而Bian[9]等人基于光滑化原理,提出了一种非自治的光滑神经网络来解决非光滑伪凸优化问题,但该模型的初始点必须在等式可行域内.

以上研究的非光滑问题,都必须满足Lipschitz连续性来定义Clarke稳定点[10],所以往往无法用来解决在现实世界中广泛存在着的非Lipschitz连续优化问题,例如稀疏表示、图像复原、信号恢复、变量选择等问题[11-15].在这些问题中,l2-lp问题得到广泛关注,当p=1时,它是l2-l0问题的最佳凸近似,而当p∈(0, 1)时,它被发现在许多稀疏恢复问题中拥有比p=1时更好的表现[16-18].但由于p∈(0,1)时的非Lipschitz性,找到l2-lp问题的全局最小点被证明是强NP难的[19].Bian和Chen[18]为了解决一类带有盒约束的l2-lp问题提出了一种光滑神经网络.Li和Bian在文献[20]中定义了一种非Lipschitz的广义平稳点,并提出了一种基于光滑化的投影神经网络去解决一类带有线性不等式约束的非Lipschitz问题,但是线性不等式约束的投影算子往往难以计算.Yu[21]等人提出一种基于罚函数的光滑神经网络,不再需要投影算子,可惜仍然依赖精确罚参数. Zhao[22]等人提出一种平滑惯性神经动力学方法构建的神经网络来解决lp范数最小化问题,但模型只适用于线性等式约束的优化问题,具有一定局限性.

在诸多学者先前工作的基础上,本文提出一种基于光滑化和微分包含理论的神经网络,用以解决一类具有线性不等式约束的非Lipschitz优化问题.与现有的解决此类问题的神经网络相比,本文提出的神经网络模型具有以下优势：

1)模型不需要提前计算精确的罚参数.

2)无需限制神经网络的初始点选取.

3)神经网络结构简单,没有复杂的投影算子.

2 问题描述与预备知识

2.1 问题描述

本文研究的非Lipschitz优化问题如式(1)所示：

(1)

其中f：n→+是连续可微函数,在可行域内有下界;φ：+→+在++上连续可微函数,且在+上全局Lipschitz连续,其Lipschitz常数为lφ;A∈r×n,b∈r,p∈(0,1).记D=(d1,d2,…,dn)∈n×m,di是D的第i列,+表示非负实数的集合,++表示正实数的集合.

这里给出一个全文假设：

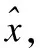
2.2 预备知识

这里为了方便读者理解,在这部分给出与本文相关的一些知识和定义.关于局部Lipschitz连续、Clarke广义梯度和法锥的定义参考文献[10],在此不再赘述.

定义1[20].对于x*∈S,如果x*满足：

定义2[23].令h：n→是一个连续函数,如果满足下列条件,那么称n·++→是h的一个光滑函数：

1)对于任意给定的μ∈是连续可微函数,对于任意给定的x∈在μ∈++上是可微函数;

2)对于任意给定的x∈

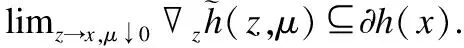
在提出神经网络模型之前先需要对目标问题进行光滑化处理.对任意s∈,μ>0,定义|s|的光滑函数为：

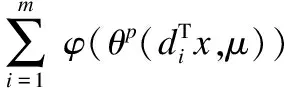
(2)

接下来引入光滑函数的一些性质.

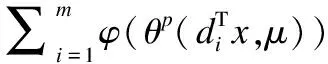
1)对于∀x∈

2)对于∀x∈≤mlφμp;

4)如果φ′在++上全局(局部)Lipschitz连续,那么对于任意给定的μ>0,有关于x全局(局部)Lipschitz连续.

3 神经网络的提出

首先构建惩罚函数如下：

(3)

其中gi(x)=Aix-bi,Ai表示A的第i行.易知式(3)是凸函数,且S={x∈n：G(x)≤0}.对于任意x∈n,都存在∂G(x),有：

(4)

其中,I0={i∈{1,2,3,…,r}：gi(x)=0},I+={i∈{1,2,3,…,r}：gi(x)>0}.

基于上文罚函数的定义,本文提出如下神经网络模型：

(5)

表1 与现有神经网络相比Table 1 Compared with existing neural networks

如表1所示,神经网络(5)与现有模型相比,约束条件更加宽松,没有限制初始点选取范围,不需要计算精确罚参数和投影算子,具有一定优势.

4 主要定理和证明

4.1 全局解的存在性

接下来给出需要用到的部分引理以保证证明的连贯性.

引理2[10].如果V：n→在x处是正则函数,x：→n在t处是可微函数,且是Lipschitz连续的,那么有：

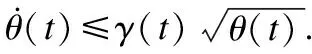
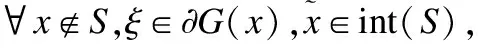
定理1.若假设P成立,对于任意的初始点x0∈n,神经网络(5)存在全局解.并且对于任何状态解x(t),存在一个足够大的R使得

证明：因为∂G(x)是非空紧凸的上半连续集值映射,神经网络的右边是一个非空紧凸的上半连续集值映射,所以对于任意的初始点x0∈n,存在一个时间T和一个连续函数x：[0,T]→n,使得x(t)是神经网络的一个局部解,其中[0,T)表示解的最大存在区间[26].

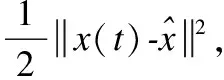
(6)

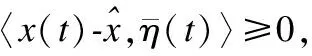
(7)

结合引理3得：

(8)

显然式(8)表明x(t)在[0,T)上有界.根据解的可拓展性,可知神经网络(5)的状态解全局存在.

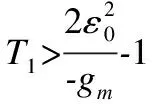
(9)

(10)

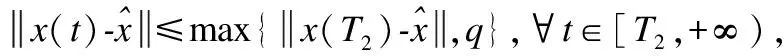
4.2 有限时间内收敛到可行域S

定理2.若假设P成立,对于任意初始点x0∈n,神经网络(5)的轨迹将会在有限时间内进入到可行域且不再离开.

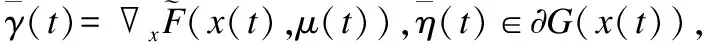
(11)

根据引理4和定理1,可以得到：

(12)

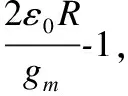
(13)

对式(13)的两侧求从T3到t的积分：

(14)

所以存在一个时间T4≥T3,使得G(x(T4))≤0,对于任意初始点x0∈n,神经网络(5)的轨迹在有限时间T4进入到可行域S.

接下来需要证明x(t)在t>T4时,神经网络(5)的轨迹进入可行域后,便不再离开.

假设存在t2>t1>T4,使得x(t1)∈S,并且x(t)∉S,∀t∈(t1,t2].

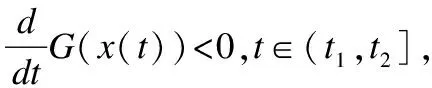
值得一提的是,本文提出的神经网络模型与有些需要初始点在可行域内的神经网络不同,它能够任意选取初始点,保证其在有限时间内进入可行域并永驻其中,也就是说不需要额外的操作来选取合适的初始点.

4.3 神经网络收敛到广义稳定点

引理5[27].对于任意的x∈S,在x处的法锥可以表示为NS(x)={ATγ：γ≥0 and(Ax-b)Tγ=0}.

定理3.若假设P成立,对于任意初始点x0∈n,神经网络(5)的解有以下性质：

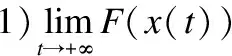
2)x(t)的任何聚点是原始问题(1)的广义稳定点.

3)如果原始问题(1)的聚点是孤立的,那么x(t)收敛到问题(1)的一个广义稳定点.

证明：

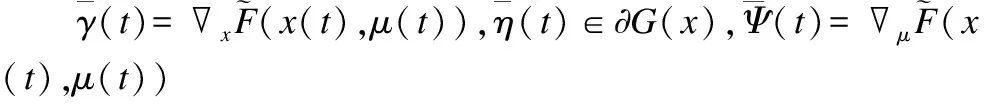
(15)

由G(x(t))=0,∀x(t)∈S和引理2可知：

(16)

又由式(15)、式(16)和引理1得：

(17)

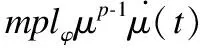
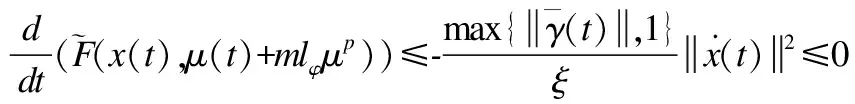
(18)

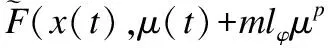
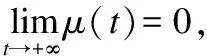
(19)

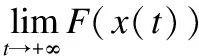
再对式(18)两边积分,得到：

(20)

从而有：

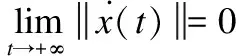
(21)

2)由可行域S的有界性可知,x(t)存在至少一个聚点.设x*是x(t)的任意一个聚点,存在一个时间序列t∈{tk}(k→+∞,tk→+∞),使得：

(22)

更进一步,根据神经网络微分包含式(5)得到：

(23)

由式(4)和引理5可知,存在ζ∈n,使得当x*∈S时：

(24)

此处ζ满足ζi∈{i：Aix-b<0}=0,ζi∈{i：Aix-b=0}≥0.

又根据定义1和式(2),有：

(25)

联立式(23)～式(25)得到：

(26)

所以x*是优化问题(1)的一个广义稳定点.

3)如果优化问题(1)的广义稳定点是唯一的,那么显然结论成立.如果优化问题(1)的广义稳定点是孤立但不是唯一的,可以使用反证法证明.

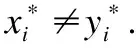
5 仿真实验

本节在MATLAB R2018b平台上进行3个仿真实验,来展示神经网络(5)解决目标问题的良好表现.

5.1 盒式约束的数值实验

考虑如下优化问题：

s.t.x∈S：={x∈S：xi∈[l,u],i={1,2,3,4,5}}

(27)

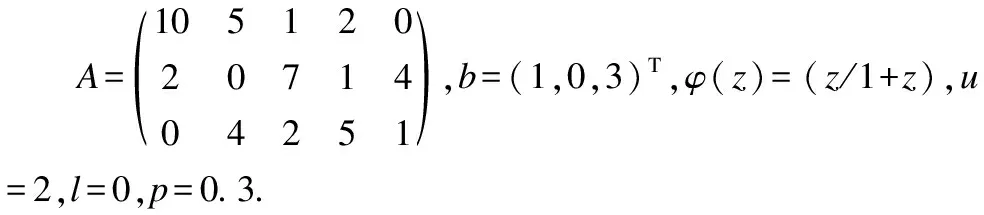
问题(27)是一个具有盒式约束的非光滑非Lipschitz优化问题,有着广泛的应用场景,但由于其具有非Lipschitz性,导致此类问题的求解较为困难.本文所提出的神经网络(5)对于解决此类问题有着不错的效果,如图1所示,实验选取ε0=μ0=1,任意选取5个未必在可行域内的点作为初始点,状态向量都收敛到点x*=(0,0,0,0.5645,0)T.

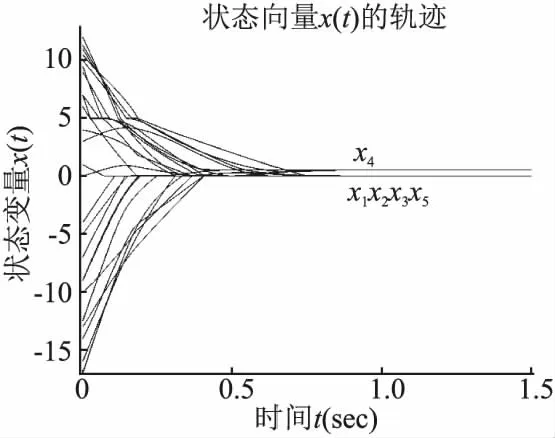
图1 神经网络(5)在不同初始点的状态轨迹Fig.1 State trajectories of neural network(5)at different initial points

另外使用神经网络(5)与文献[18]所提出的光滑神经网络(SNN)进行对比实验.设置两个神经网络模型的初始点为x0=(-17,10,9,4,-5)T,实验结果如图2所示,可以看到神经网络(5)具有与SNN相似的收敛效果.

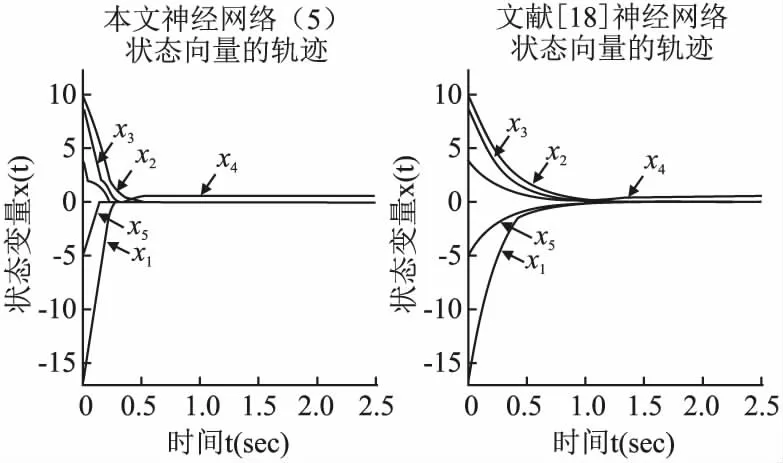
图2 神经网络(5)与文献[18]神经网络状态轨迹对比Fig.2 Comparison between neural network (5) and state trajectories of neural network in reference[18]

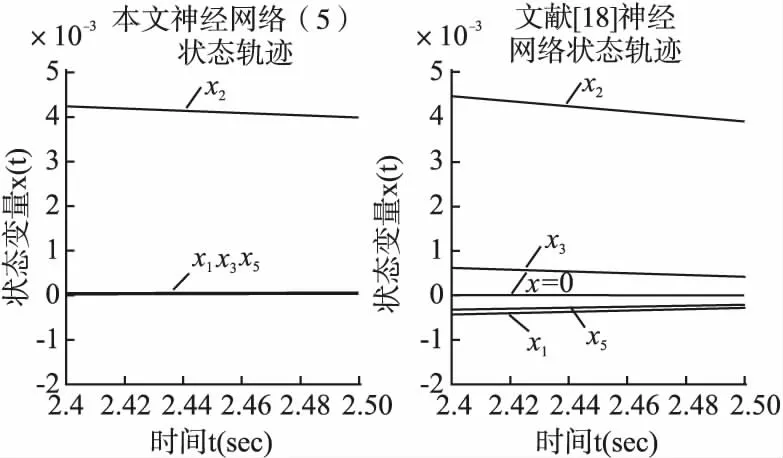
图3 状态解局部轨迹对比Fig.3 Comparison of local trajectories of state solutions

由上述的实验结果可以看出,神经网络(5)能够有效解决此类具有盒式约束的非Lipschitz优化问题,并且有能够任意选取初始点的优势.

5.2 线性不等式约束的数值实验

考虑如下优化问题：

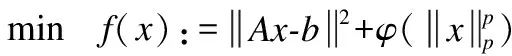
s.t.x∈S：={x∈S：Bx≤c}

(28)

其中：

b=(1,0,3)T,c=(1,1,1,1,1,0,1,1,1)T,φ(z)=(z/1+z),p=0.3.

问题(28)是一个非光滑非Lipschitz优化问题,该问题具有线性不等式约束,用一般方法较难处理这类问题,而本文所提出的神经网络(5)能够较好地解决这类问题.

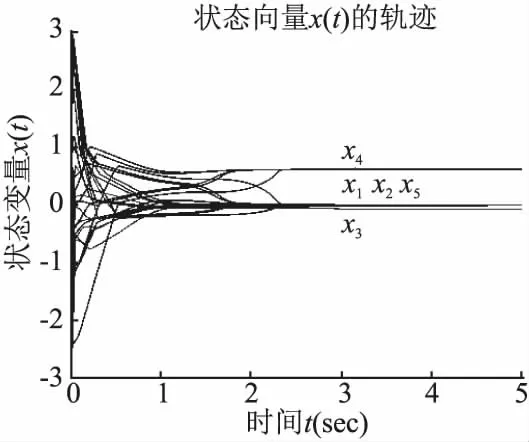
图4 神经网络(5)在不同初始点的状态轨迹Fig.4 State trajectories of neural network(5) at different initial points

实验中选取ε0=μ0=1,随机在xi∈[-3,3]范围内任意选取5个未必在可行域范围内的初始点,由图4可知,无论初始点如何选取,最终状态向量x(t)的轨迹都收敛到(0,0,-0.0790,0.6147,0)T.

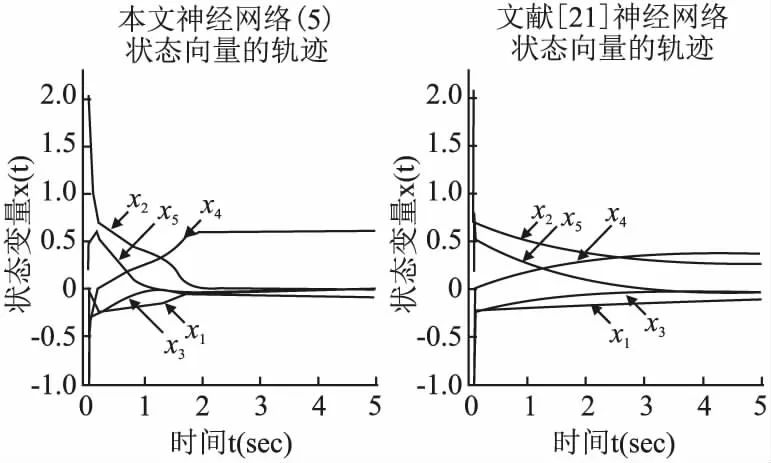
图5 神经网络(5)与文献[21]神经网络状态轨迹对比

为了验证神经网络(5)的有效性和优势,选取文献[21]中的神经网络模型与本文模型对比.值得说明的是,文献[20]中的投影神经网络(PNN)在解决这类问题时,较难计算线性不等式可行域的投影算子,并且同实验5.1中的SNN一样,无法任意选取初始点.

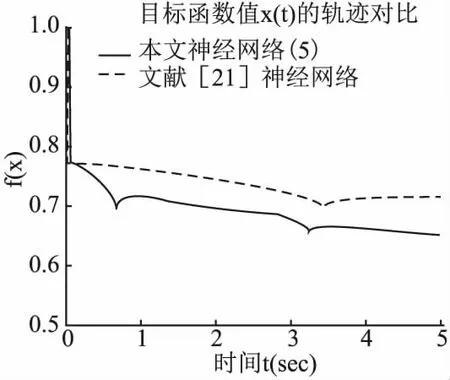
图6 神经网络(5)与文献[21]神经网络目标函数值对比Fig.6 Comparison between the objective fuction value of neural network(5)and neural network in reference [21]

对比实验选取(-1,2,-1,-1,0.2)T作为初始点,两类神经网络的状态解收敛轨迹如图5所示,能够看出文献[21]中的神经网络状态解收敛到与本文神经网络(5)的状态解不一样的位置.而通过图 6中显示出的两类神经网络状态解的目标函数值f(x)的变化轨迹,能够看出神经网络(5)的显然小于文献[21]的神经网络.也就是说,在解决这类问题时,本文神经网络(5)具有良好表现,而且并不需要计算罚参数来保证神经网络的收敛,具有一定的优越性.

5.3 图像恢复实验

在实验中,通过对64×64像素的退化观测图像进行复原验证神经网络(5).图7中的(a)和(b)分别展示了原始图像和退化的观测图像,观测图像的退化是由于模糊和随机噪声导致,其中模糊核由7×7尺寸的二维高斯函数h(i,j)=e-2(i/3)2-2(j/3)2构造,随机噪声由零均值、0.05标准差的高斯噪声组成.退化后图像的PSNR为15.57dB.

图7 原始图像和观测图像Fig.7 Original image and observed image

将上述图像复原问题建模为如下优化问题：

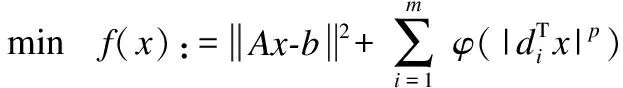
(29)

其中,n=642,A∈n×n是由模糊核构造的模糊矩阵,b∈n是观测图像,n表示图像的一阶微分算子矩阵D的第i列.矩阵A和D分别由文献[28]和文献[12]中的方法构造.

图8 复原图象Fig.8 Restored images

在该实验中,令μ0=1,x0=b,使用神经网络(5)分别在p=0.3和p=0.5的情况下进行复原,复原效果如图8所示.在图 9中给出了神经网络(5)的PSNR变化轨迹,可以看出当p=0.3时,具有更好的效果.

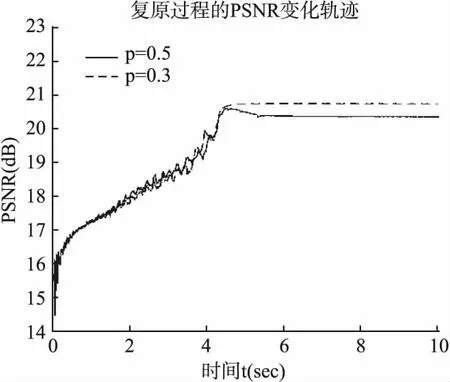
图9 p=0.3和p=0.5时PSNR的变化轨迹Fig.9 Trajectories of PSNRs with p=0.3 and p=0.5

与文献[12]中的GNC算法和文献[17]中的SPG算法的PSNR对比如表 2所示,显然神经网络(5)在处理问题(29)时更具优势,证明了本文的神经网络模型在处理这类图像复原问题时具有良好表现.

表2 PSNR与其他算法的PSNR对比Table 2 Comparison of PSNR with other algorithms

6 结 论

本文为了解决稀疏优化领域中常见的一类非光滑非Lipschitz问题,提出一种新型的光滑神经网络模型,在文中证明了所提神经网络的状态解全局存在,并能够在一个有限时间进入可行域内不再离开,还证明了神经网络的任意聚点都是目标问题的广义稳定点.与现有神经网络相比,该模型不需要计算投影算子和额外的罚参数,结构简单,任意选取初始点,具有一定的优越性.最后,通过数值仿真实验展示了所提神经网络对目标问题的有效性,并且通过图像恢复实验展示了它应用在实际问题中的良好表现.