基于CIPP评价模型的高中数学教师教学反思评价体系构建研究

杨 凡 (北京市通州区通运小学 101100)

康玥媛 (天津师范大学教育学部 300387)

1 引言

近年来,教师专业发展已成为国际教师教育界的热门话题,教学反思作为教师专业发展和自我成长的核心因素,在各国教师注册和专业标准中被多次提及．“全美专业教学标准委员会”(NBPTS)制定的教师评价指标体系,强调教师应“系统地进行反思,并从经验中学习”．加拿大BC省于2019年颁布了《不列颠哥伦比亚省教育者专业标准》,要求“教师要参加专业学习、教学实践和教学反思,以支持自身的专业化发展”．

在我国,教育部2012年颁布了《中学教师专业标准(试行)》,要求教师“坚持实践、反思、再实践、再反思,不断提高专业能力”[1]．2017年,教育部办公厅印发了《中小学幼儿园教师培训课程指导标准(义务教育语文学科教学)》等3个文件,分别在实践课程、教学研究与改进等专题强调了教学反思的重要性．2022年,教育部等八部门印发了《新时代基础教育强师计划》,提到要服务教育高质量发展要求,加强高质量教师队伍建设．可见,教学反思作为教师的专业能力之一,对教师的专业化成长及教师队伍建设起着重要作用．

就已有研究来看,有依据范梅南(Van Manen)对反思水平的划分构建的教师课后反思评价指标体系[2],有从课程的构成要素出发构建的视频分析框架支持下的中小学教师教学反思维度[3],再有结合“互联网+”时代背景构建的乡村教师教学反思能力检核模型[4]．但就已有的教学反思评价体系来看,存在缺少学科和学段划分的有效凸显、评价标准表述不明确等问题,故需进一步研制具有明确指向性的高中数学教师教学反思评价指标体系．

本研究在已有文献的基础上,聚焦数学学科,以高中学段为例,进行教师教学反思评价指标体系的构建研究,从而进一步丰富研究内容,提升教师教学反思评价的科学性．

2 概念界定与理论基础

2.1 概念界定

从词源的角度看,《现代汉语词典》将“反思”解释为“思考过去的事情,从中总结经验教训”．《柯林斯英汉双解大词典》中reflect或rethink都解释为“反思”,前缀re-代表再一次,可以看出“反思”是再一次思考、回顾的意思．

从心理学的角度看,教师对教学实践的反思是一种内隐的元认知过程,使教师能够针对教学实践及时进行评价、反馈教学活动中的有关信息及结果,从而发现问题,进行改正．

在学术界,国内外许多学者都对反思的概念进行了探索和研究．杜威(Dewey)最早提出了反思概念,即“个体在头脑中对问题进行反复、严肃、执着的沉思”[5]．我国学者赵明仁将教学后反思分为“回顾”“研究”“再理论化”三类[6]．

与教师在教学活动中内隐的反思相比,教学后反思更具有外显性、可测量性与可操作性．故本研究关注教后反思,以教学设计中最后的教学反思模块为研究主体,选取教师的“回顾”维度,概括出教学反思的概念,即教师积极主动对已结束的教学活动进行评价、回顾并产生新理解的认知过程．

2.2 理论基础

科学地评估高中数学教师教学反思离不开好的评价模型,研究选取CIPP评价模型作为理论基础．

CIPP评价模型由美国学者斯塔弗尔比姆(D.L.Stufflebeam)提出(图1)．三个同心圆描绘了模型的基本元素,内圈代表核心价值．围绕价值观的圆环分为四个评价焦点:目标、计划、行动和结果．外圆环表示服务于四个评价焦点的评价类型:背景评价(context evaluation)、输入评价(input evaluation)、过程评价(process evaluation)和结果评价(product evaluation),双向箭头揭示了特定评价焦点和评价类型之间的关系[7]．总之,CIPP评价模型符合教学反思评价的要求及目标,为构建高中数学教师教学反思评价体系提供了一个框架．

图1 CIPP评价模型

3 基于CIPP评价模型的高中数学教师教学反思评价体系构建

3.1 理论分析下评价体系的初步构建

通过对已有指标体系的梳理,遵循评价指标体系设计的系统性、科学性、导向性与可行性原则[8],以CIPP评价模型的四维度为框架,将高中数学教师教学反思评价体系的一级指标初步确定为:教学背景、教学准备、教学过程、教学成效．

以基于背景评价的教学背景为前提,对一节课的定位、背景和对象进行诊断性评价,将“教学背景”维度细化为课标要求、教材内容、学生情况3个二级指标．以基于输入评价的教学准备为出发点,对教学方案的可行性与有效性进行评价,将“教学准备”维度细化为教学目标、重点难点、资源配置3个二级指标．以基于过程评价的教学过程为核心,根据教学活动的构成主体,对课堂中教师的教与学生的学进行形成性评价,将“教学过程”维度分解为教师教学、学生学习2个二级指标．以基于成果评价的教学成效为关键,根据课程的构成要素,对教学活动中的教师与学生的收获、体验,教学的效率与成果等进行总结性评价,将“教学成效”维度分解为教师发展、学生发展、教学效率和课堂文化4个二级指标．

基于理论分析初步拟定的高中数学教师教学反思评价体系由4个一级指标、12个二级指标构成(图2)．

图2 高中数学教师教学反思评价指标

3.2 德尔菲法下评价体系的修订完善

3.2.1专家组成

为了保证指标体系的科学性,采用德尔菲法向相关领域专家进行意见征询,专家数量在10～50位为宜[9-10],专家的选取遵循以下要求:充分理解所调查的内容;在数学教育领域有所建树,具有丰富的数学教育类理论或数学教学实践经验;具有作答和反馈时间．最终确定17位征询专家,基本情况如表1．

表1 专家基本情况

3.2.2专家评价

采用Excel和SPSS软件,计算专家的积极系数、专家的权威程度系数及专家意见的肯德尔协调系数,以保证德尔菲法运用的科学性与有效性．

(1)专家的积极系数．专家的积极系数用问卷的回收率来表示,第一轮运用德尔菲法向17位专家发放问卷,回收了14份有效数据,回收率为82.35%．第二轮发放了17份问卷,回收了14份有效数据,回收率为82.35%．在两次意见征询中,专家积极系数均大于70%,表明专家的参与度较高．

(2)专家的权威程度系数．专家对研究内容的熟悉程度(CS)及判断依据(Ca),共同决定了专家的权威程度系数(Cr)．依据统计学的要求,Cr≥0.70时数据具有较高的可信度[11]．其中,熟悉程度系数与判断依据系数的量化值见表2．

表2 熟悉程度与判断依据的量化值

第一轮德尔菲法应用中,熟悉程度为0.74,表明专家对调查内容较为熟悉,判断依据为0.88,体现判断依据对专家的影响较大,第一轮的专家权威程度系数为0.81(>0.70),故专家对指标的评价具有较高的可信度．在第二轮德尔菲法的应用中,专家的熟悉程度为0.72,判断依据为0.88,第二轮专家权威程度系数为0.80(>0.70),可见专家对指标的评价具有较高的可信度．

3.2.3第一轮结果分析

专家对各指标的合理性意见可以通过肯德尔协调系数每个指标的均值、标准差、变异系数和满分频率进行考察．意见表采用李克特四点量表对指标的合理性进行划分．通过SPSS 13.0软件对第一轮回收的数据进行分析,专家对一级指标设定合理性的意见均值为3.64,一级指标合理性较高．通过对二级指标意见的数据进行分析发现,资源配置、教学效率、课堂文化3个指标均值低于3.50,标准差大于0.5,变异系数大于0.2,较不合理,需要结合专家意见修订．

修订后,一级维度不变,删除“资源配置”与“教学效率”两个二级指标,将“教材内容”改为“教材理解”,在教学准备维度下加入“流程设计”,将“课堂文化”指标调至“教学过程”维度下．修订后的体系由4个一级指标、11个二级指标构成．

3.2.4第二轮结果分析

将修改后的评价体系再次以电子邮件形式向专家发放问卷,得到第二轮数据结果．经统计,一级指标合理性的均值为3.71,标准差为0.47,变异系数为0.12,小于0.2,满分数量多于一半以上,综合两轮调查判断一级指标的设定合理．第二轮二级指标的分析结果如表3所示,各个指标的均值均大于3,标准差均小于1,变异系均数小于0.2,符合统计学要求．

表3 第一轮德尔菲法二级指标合理性的结果分析

第二轮意见征询中,结合专家意见对“教学目标”“课堂文化”的评价标准进行了完善,最终形成了由4个一级指标、11个二级指标及指标评价标准所构成的评价指标体系(见附录)．

3.3 文本分析法下评价体系的检验

3.3.1反思文本的选取

为保证教学反思样本的可分析性,以《普通高中数学课程标准(2017年版)》作为指导的三本出版物和在中国知网(CNKI)已公开发表的教学课例文章为载体,选取教学设计中的教学反思(或称教学后记、教学感悟)部分作为编码对象．所取样本含盖必修课程中预备知识、函数、几何与代数、概率与统计四大主题,选择性必修课程中函数、几何与代数、概率与统计三大主题．在课程类型上,囊括了章引言课、概念课、命题课、复习课与探究课五种课型,覆盖面广,具有很好的代表性,样本来源及数量见表4．

表4 教学反思样本的选取

3.3.2编码过程与结果

借助NVivo11软件对73篇高中数学教学反思文本编码的基本流程为:文本导入→文本编码→编码检验→汇总结果[12]．

编码过程中形成了一个多层级树状结构,其中一级节点对应评价体系的一级宏观指标,二级节点是在其基础上的细化,为体系中的二级指标,三级节点则是从教学反思样本中所提取的原始信息．在完成编码后,利用预留的8篇样本进行饱和度检验,未发现新的维度,验证了编码结果的严谨性和解释力．此外,研究由两位编码人员独立进行编码,经计算编码一致性均在80%以上(表5),符合编码要求．

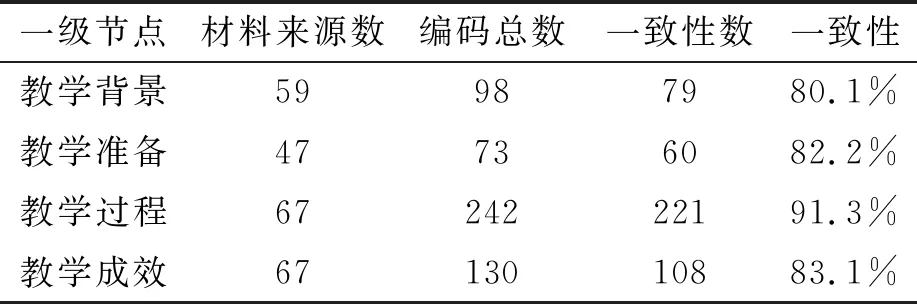
表5 教学反思文本编码的一致性检验

4 基于层次分析法的高中数学教师教学反思评价模型构建

4.1 评价模型的构建

指标权重的计算是评价模型构建的一部分,研究选择层次分析法进行权重的计算．以评价体系作为框架,将各级指标进行两两比较,编订《高中数学教师教学反思评价指标权重问卷》,采取电子邮件的形式向高校中研究方向为数学教育(教师教育)的教授及副教授、有高级及以上职称的高中数学教师共14位专家发放问卷,收回13份有效问卷,回收率为92.9%,计算流程如图3．

图3 基于层次分析法计算指标权重流程图

选取其中一个原始矩阵(表6)详细介绍一级指标权重的计算过程[13]．

表6 专家W的一级指标判断矩阵

第4步 进行一致性检验.

这说明该判断矩阵相对合理,结果一致性较好,由专家W所确定的一级指标权重依次为0.072 1,0.072 1,0.392 0,0.463 8．根据以上方法,将所有专家的数据转化为判断矩阵进行计算和检验,最后将专家对每一个指标归一化后的权重进行相加再除以专家总人数,得到相应指标的对应权重值．

为了保证计算结果的准确性,利用yaahp软件加以验证,如果某个判断矩阵出现不一致的情况时,该软件可以在最大限度保留专家决策数据的前提下标注需要修正的判断矩阵,从而进一步进行自动修正,在一定程度上避免人工调整判断矩阵的盲目性．根据计算后的一级、二级指标的权重值建立具有层级关系的评价模型(图4)．根据加权平均法,得到高中数学教师教学反思评价模型S=0.033 8B1+0.029 1B2+0.046 2B3+0.055 5B4+0.043 3B5+0.048 4B6+0.137 7B7+0.163 1B8+0.068 5B9+0.162 0B10+0.212 4B11．

图4 层析分析法下高中数学教师教学反思评价结构模型

4.2 评价模型的检验

通过评分者一致系数对该评价指标体系的信度进行检验[14]．将以上数据依次输进SPSS软件中,通过非参数检验计算肯德尔协调系数,结果为0.760(p=0.022<0.05),具体结果见表7,说明评分者一致性可以达到95%以上,一致性良好,具有良好的可信性,这代表《高中数学教师教学反思评价指标体系》信度合理．

表7 《基本不等式》教学反思指标评价结果统计

在此基础上对内容效度进行检验．内容效度是指一个量表实际测到的内容与所要测量的内容之间的吻合程度[11],研究选择通过计算量表的条目水平内容效度指数(I-CVI)和整个量表水平的内容效度指数(S-CVI),来进行指标体系内容效度的评估．

研究参照Lynn给出的I-CVI的判断标准,当专家人数等于5人时,I-CVI的数值权威达到1.00,才认为这个条目的内容效度较好．考虑到存在随机性的原因,根据不同专家人数下的I-CVI值估计表进行随机一致性校正[9],得到指标模型内容效度的整体结果(表8)．

由表8可知,进行随机一致性校正后,K*为0.760(>0.740),所测内容与欲测量内容之间有较好的相关性,内容效度优秀,因而该高中数学教师教学反思评价模型可靠．

表8 评价模型内容效度整体结果

5 结语

综上,高中数学教师教学反思评价体系与评价模型的构建,不仅可以作为衡量教学反思现状的工具,也可以作为教师教学反思能力发展的标尺．通过合理使用该工具,能较为客观地评价和考核教学反思的现状和发展趋势,进而研究和把握高中数学教师教学反思发展的微观特征与宏观趋势,借助结果反馈,推动教师的“思”“行”统一,促进专业发展．