HPM视角下基于“大概念”的高中函数概念教学探索*
张海波 (广东省惠州市惠东县惠东中学 广东省谭光友名师工作室 516300)
数学学科大概念(big idea)是指能反映数学学科本质及其特殊性的、构成学科框架的原理、思想和方法的理念.作为“三新”(新课标、新教材、新高考)背景下落实学科核心素养的关键,“大概念”既为关键性概念提供认识论和方法论的意义,又统摄和包含了大量学科知识,能够体现主题内容与思想方法的整体性、系统性和联系性.因此“大概念”能有效加强学生对数学整体性的理解和对数学思想的体会,进而有效发展核心素养.HPM(数学史与数学教育关系)视角下,遵循知识的历史发生、发展规律,在教学过程中,不仅突出知识的本质属性,而且渗透了知识产生过程中所包含的思想、方法和逻辑思维.因此HPM的融入,不仅能突出知识背后的思想、方法等,而且还能有效防止知识的碎片化,体现主题内容的整体性、联系性.在“大概念”的指引下,融入HPM,使得主线、主题、章节、课时间的核心概念、基本知识等产生了内在必然的联系,不仅能够增强学生对数学知识整体性的理解,也能起到发展学生核心素养的目的.
因此,HPM视角下基于“大概念”的教学理念,能帮助学生整体理解数学知识,领悟其中的数学思想、方法,从而为核心素养的发展提供一个逻辑贯通且具有可操作性的途径.
1 “研、设、问、探、评”的设计策略
首先,“研”是深入研究课程标准、新教材,并提炼出该主题的“大概念”.“大概念”是指能反映数学本质,构成学科整体性框架、思想和方法的上位知识.新课标是实施教学的准则,课程专家在制定、编写课程标准和教材时,必会融入其在数学思想、方法、学科本质、学科框架等方面的见解,这些见解就是学科专家概括出的“大概念”,而学科大概念能够将数学的关键思想方法和相关核心概念联系起来,从数学学科的本质特征上整体把握每一课时的教学.因此,研究新课标、新教材等是提炼“大概念”的理论基础.其次,“设”是指教师要在HPM和大概念理念的引领下创设一个蕴含数学本质的情境,将待解决的问题蕴含在情境问题中,学生在对问题进行分析、类比和归纳概括的过程中抽象出核心概念.再次,“问”是指教师要基于情境与核心概念,设计出指向核心概念生成的“问题串”,以此引导学生摒弃概念中的非本质属性,保留数学的本质属性,领悟其中的数学思想,发展核心素养.接着,“探”是通过数学中的具体情境或实际生活中的问题,探究利用概念解决问题的过程,以加深学生对概念本质属性的理解.最后,“评”是评价学生迁移、应用知识的情况.
2 教学探索——以函数概念的五个维度为例
2.1 研:研究新课标、新教材,以提炼“大概念”
“研”是研究课程标准、教材,并提炼函数主题的“大概念”.“大概念”是从知识的本质内涵出发,基于数学整体性的思想、方法、知识结构、逻辑等角度凝练而来.
那么,函数主题的“大概念”内涵是什么呢?带着这个问题统览新课标及教材有关“函数”的内容,从函数主题的学科整体性思维,学科研究框架,整体性思想、方法和发展核心素养等角度入手,凝练如下:
新课标对函数内涵的定位:函数是描述客观世界中变量关系和规律的最基本的数学语言和模型[1].
整个主题的教学结构是:学生理解一般函数的概念—研究一般函数性质—掌握一些具体的基本初等函数模型—知识的应用和迁移.通过函数主题的学习,渗透和运用其包含的思想方法:运动变化、数形结合、运算思想等.提升的数学学科素养包括:数学抽象、数学建模、数学运算、直观想象、逻辑推理[2].
基于新课标、教材的整体性分析,为更好凝练“大概念”的内涵,在教学前需要思考以下问题:(1)函数概念的本质属性是什么?(2)它与本单元、主题、主线的其他内容有什么联系?(3)函数概念教学蕴含什么数学思想方法?能发展学生什么核心素养?(4)本单元整体的研究框架、研究思路和手段是什么?(5)在HPM视角下,函数概念是如何产生的?如何通过数学史体现函数的研究思想和本质属性?(6)对培养学生的价值观有什么作用?思考这些问题有利于从数学知识的整体结构、核心内容、重要思想上凝练出学科“大概念”.
本主题整体的研究框架:创设情境—抽象概念—研究性质—迁移应用.
整体研究思路:(1)从一般到特殊(从一般函数到基本初等函数、从连续函数到离散函数);(2)从具体到抽象(从典型丰富的具体情境抽象出概念);(3)从定性到定量(从直观表述到精确的定量描述).
核心素养发展视角下的概念教学:提供典型丰富的情境(数学建模)—数学分析、类比(数学抽象、直观想象)—归纳共同属性(逻辑推理)—抽象概括出概念(数学抽象).通过建模、抽象、推理、运算等手段,体现出概念教学的一般过程和手段.
概念教学的研究路径:情境问题的分析—共性归纳—保留数学本质—下定义—概念辨析—数学问题或实际问题中的应用.
除了这些明线以外,本单元还隐藏一条暗线:情境—方法—方法论—数学学科本质.基于具体情境问题,通过分析、归纳、抽象等方式研究函数,得到一种研究方法,从本主题整体分析,进而形成研究的方法论,最后借助这种研究方法认识函数的本质,加强数学学科的本质观念[2].
在数学思想方法方面:从认识函数概念的不同角度,渗透数形结合、运动变化等数学思想.例如,从函数解析式认识函数或在坐标系中将函数看成由点组成的“图形”,从几何和代数这两种认识函数的角度,有效承载了数形结合的数学思想.从数学知识的关联性分析,后续研究函数的性质也是利用数和形的结合展开的.
在核心素养渗透方面:本单元从情境到概念的研究过程,发展了学生数学建模、数学抽象、直观想象、逻辑推理等核心素养.
核心价值方面:从HPM视角看,伟大的数学家在某一阶段也出现了函数就是解析式这一认知障碍,这能够增强学生信心,让学生感受到数学的发展也是有温度的;数学家们在认知上的障碍,也是现在学生容易出错的点,这能有效促进学生自我反思;历史上数学家通过不同角度认识函数概念,而函数描述运动变化的属性没有改变,这也能培养学生的辩证唯物主义思想.
以上几大方面都是“大概念”理念的集中体现,也是本课时教学中应该突出的关键点.
2.2 设:创设情境,抽象核心概念
在以上“大概念”的指引下,为了凸显概念的发生、发展过程,突出其数学本质,首先创设一个数学情境——函数发展的历史过程.以历史发展为背景,在函数历史发展过程中感悟函数的本质属性.首先课前让学生了解函数的五个发展阶段:
(1)16世纪,随着解析几何的发展,阿波罗尼奥斯等数学家运用曲线上一个点相关的量,形成了早期的函数思想萌芽.
(2)17世纪,莱布尼兹首先使用“函数”一词,函数的概念从几何形态走向代数形态.欧拉等伟大的数学家认为,函数就是一个解析式.
(3)18世纪,狄利克雷、傅里叶认为函数的概念应该突破解析式的限制,用变量对应说定义函数.
(4)19世纪,康托集合理论诞生,布尔巴基学派用集合对应关系说来定义函数,这就是现在高中学习的函数概念.
(5)为了进一步符号化和抽象化,现代函数的概念用两个集合的笛卡尔积来定义,因过于抽象,将在大学课程中介绍.
从函数的历史发展进程可以感悟出,函数概念发展的本质就是一个不断抽象的过程!通过不断去掉非本质属性,保留其数学本质特征,得到蕴含数学本质属性的函数概念,让学生体会抽象是数学概念发展必不可少的步骤.
HPM的融入,让学生体会到数学并不死板和是一成不变的,它是不断发展的,每一个概念的产生都蕴含着几代伟大数学家的心血,数学的每一次前进都是不断探索和进步的结果,让学生体会到数学的温度,凸显数学人文的一面.与此同时强调数学的发展是永无止境的,当然函数概念也会随之继续扩展,激发学生进一步探索的欲望.通过历史知识的融入,学生很容易发现:初中的函数概念处在第(3)阶段,而高中学习的函数处在第(4)阶段.为何高中要进一步发展函数概念?如何得到高中函数的概念呢?
为了解决以上疑惑,需要创设具体的情境问题:正方形周长为l,边长为u,则l=4u和正比例函数y=4x相同吗?解析式不同的两个函数f(x)=1与f(x)=sin2x+cos2x是否相同呢?显然初中函数概念无法解决,因此强调进一步拓展函数概念是非常必要的.
那么,如何得到高中函数的概念呢?需要创设四个情境(直接使用教材例子),通过分析、归纳和概括问题情境中的共性,抽象出函数概念的本质属性.
情境1 “复兴号”高铁运行问题.
情境2 某公司维修工人工资问题.
情境3 北京某天空气质量指数变化图.
情境4 我国某镇居民十年恩格尔系数情况变化数据表格.
为了抽象出函数的概念,在“大概念”的指引下,本主题概念教学的通用思路为:感性具体—理性具体—理性一般.针对以上四个感性具体的情境,首先是由感性具体到理性具体的抽象思路,即分别对每个情境问题进行首次抽象(用更加规范、准确的数学语言来描述每一个具体的情境问题),用“集合间的单值对应”来描述每一个具体问题,以此凸显概念的本质属性.例如,情境1、情境2突出了定义域属性的重要性;情境3、情境4凸显函数对应关系属性的核心意义,也隐含了值域可以是集合B的子集这一属性.经过以上思路抽象以后再让学生分析、类比,归纳概括出四个情境中的共同特征,进而得出一般函数的概念,这就是理性具体到理性一般的研究思路!
另外,从整体性的角度出发,本单元其他核心概念的形成也遵循该研究思路,它起到一个统领本单元的作用.例如,函数单调性的概念,通过具体函数f(x)=x2的问题情境,先从图象得到感性具体描述,经过首次抽象,用精确的数学符号语言描述,即理性具体,再用两个具体函数进行同样操作,通过归纳、概括它们的共同特征,抽象出一般函数单调性的概念,即理性一般.因此在“大概念”教学理念的指引下,不仅能构建融数学知识、思想、方法为一体的数学体系,还能更好地帮助学生领悟数学的思维.
2.3 问:设置问题串,发展核心素养
通过对情境的分析,设置启发学生思考的问题串,引导学生舍去非数学的属性,感悟概念的数学本质,同时发展数学抽象、数学建模、逻辑推理等核心素养.
为了指引学生在概念抽象过程中能顺利舍去非本质属性,需要设置指引性的问题串.例如,针对情境1,可以设计问题串:从初中函数概念的角度分析,s是t的函数吗?能说1 h后,列车前进350 km吗?你能回答1 h后前进的距离吗?t的范围是什么?s的变化范围?如何更加精确描述s和t之间的关系?通过问题串,让学生不自觉地关注其本质属性,感悟其中蕴含的数学思想,发展数学抽象的素养.如法炮制,用类似的问题串分析情境2.通过问题串的解决,发现情境1和情境2解析式相同、定义域不同,它们是两个不同的函数.问题串的设置能帮学生明确自变量的取值范围这一属性的重要性,同时发展学生数学抽象、数学建模的素养.
对于情境3、情境4,除了设置类似问题串外,再追加提问:你打算用什么样的方式来表达该函数?以此引导学生思考:把情境3、情境4中的图象或表格照搬过来表达函数不太现实,突出引进抽象符号f(x)的必要性.另外,就图象和表格中因(自)变量范围不易观察,提出问题:你觉得该如何处理?通过问题串强调引入抽象符号f和扩大集合B的必要性,为获得函数概念做进一步的准备.
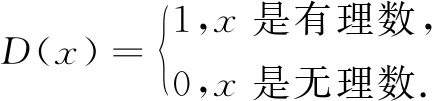
2.4 探:经历活动探究,理解概念本质
在概念教学中,千万不要着急进入机械的解题训练,应让学生经过探究、交流讨论等活动,进一步理解概念的本质.
探究活动1 对应关系f的本质内涵及引进抽象符号y=f(x)的必要性.
通过对高中函数概念的理解,各小组内相互讨论、交流,并辨析汇总.
(1)f(1)=3是什么意思?
(2)f(x)=x2+2x+1,则f(a),f(x+1)怎么理解?试用函数的概念解释.
(3)f(x)=x2与y=x2是否相同?为什么?
(4)你能确定函数y=ax2-a2x+1中谁是自变量吗?
(5)函数f(x)=ax2-a2x+1与f(a)=ax2-a2x+1相同吗?
(6)通过以上问题的讨论,你能说出为什么要使用符号y=f(x)表示函数吗?
点评通过以上问题的探究,学生能够更好地理解对应关系f的含义、抽象符号y=f(x)的内涵及其引入的必要性,理解函数概念为何要符号化[3].
探究活动2 何为同一函数?
各小组从函数概念的本质属性出发,小组内相互交流、讨论以下探究问题:
(1)有三个函数:y=x2,x∈[0,+∞);m=n2,n∈(0,+∞);x=y2,y∈R.它们相同吗?
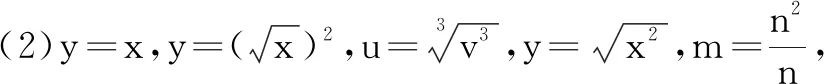
点评以上问题的交流、探究,让学生领悟同一函数的内涵就是函数的本质属性的体现,即定义域、对应关系f、值域要一样,强化概念本质属性的理解.
2.5 评:评价核心概念,促进知识的迁移和应用
在“大概念”教学理念的指引下,评价活动强调知识的迁移和应用,真正起到发展核心素养的作用.因此在教学过程中,评价活动既要关注学生数学知识技能的掌握和应用,还要关注学生核心素养的落实.通过评价帮助学生掌握概念的数学本质,体会数学思想,以此更好地迁移和应用知识,并提升素养.本节设置了两个评价活动,重点评价概念的迁移和应用.
评价活动1 判断下列两组函数是否为同一函数:①f(x)=1,g(x)=x0;②表示炮弹飞行的高度h与时间t关系的函数h=100t-4t2,二次函数y=100x-4x.
点评高中函数概念是一个符号化、抽象度高的概念,知识应用和迁移需要牢牢抓住其本质属性:①虽然对应关系和值域相同,但两者的定义域不同,故不是同一函数;②需要注意现实中的问题,其定义域根据实际情况确定,虽然两个函数的对应关系f相同,但定义域不同,故不为同一函数.该评价活动的关键是理解函数概念的数学本质,有效评价学生对函数本质的理解和应用,发展逻辑推理、数学抽象等核心素养.
评价活动2 若函数f(x)=x2+4x+2a,且f(bx)=16x2-8x+9,则函数y=f(ax+b)的值域为.
点评学生的一般思路:先用待定系数法求出参数a,b,然后求出y=f(ax+b)的解析式,再求值域.若对函数的本质属性理解透彻,就能观察到:函数y=f(ax+b)中,其定义域与题干中的函数相比,没有变化,仍是R,对应关系f也没有发生变化.因此题目中的三个函数的本质属性完全相同,故f(bx)=16x2-8x+9的值域就是所求值域.通过对函数的本质属性的深刻理解,发现它们的定义域和对应关系f都相同,因此值域就很好解决.该问题能够有效评价学生对函数概念本质属性的迁移和应用,同时发展学生数学抽象、逻辑推理等素养.
3 教学反思
HPM视角下基于学科“大概念”的教学探索,以“大概念”为引领,以HPM为情境化的内隐指导.最后从教学理念、HPM融入、数学分析三方面反思.
(1)教师应从数学的整体性角度思考,以新课标和新教材为蓝本,做好单元概念的层次分析,梳理知识间的关系,提炼出隐藏于知识背后的思想、方法、数学本质等[4],体现学科“大概念”的整体性、关联性和系统性.
(2)HPM为概念的情境化提供了内隐指导,从HPM角度出发,创设支撑概念发生、发展的情境问题,以问题串为依托引导学生思考,帮助学生领悟概念的数学本质,体会其蕴含的思想方法,进而发展核心素养.另外,数学史的融入也让数学的发生、发展变得自然,更有温度,数学也更具有人文价值.
(3)从数学角度分析.把握概念的数学本质特征,不仅是知识迁移应用的前提保障,而且也影响着本单元其他核心概念的学习.例如,函数概念中承载的数形结合的思想,也是研究函数性质的一般思想.另外,高中函数明确了定义域这一属性,不同函数可以通过四则运算得到新的函数,还可在定义域或其子区间上研究函数的性质,这为后续其他内容的研究提供了必要的保障.

