灵活应用平行四边形的性质与判定
刘丹丹



沈阳市博才初级中学邵爱平老师的直播课《平行四边形性质与判定综合应用》选自辽宁教育学院“学到汇”公众服务平台“辽宁省初中数学学科周末名师公益课堂”,旨在贯彻落实国家“双减”政策,帮助广大师生自主学习和个性化提升。
邵爱平老师的直播课,从知识梳理、典型例题、变式训练、中考链接四个方面展开,帮助同学们结合图形理解、总结平行四边形的性质及判定方法,引导同学们多角度思考,发现最优方法. 平行四边形是初中数学“图形与几何”领域的重要图形之一. 它既是平行线、全等三角形等知识的后续应用,又是进一步理解特殊平行四边形(矩形、菱形、正方形)的必要基础,为研究两条直线平行、线段相等及角相等提供了新的方法和依据.
典例探究
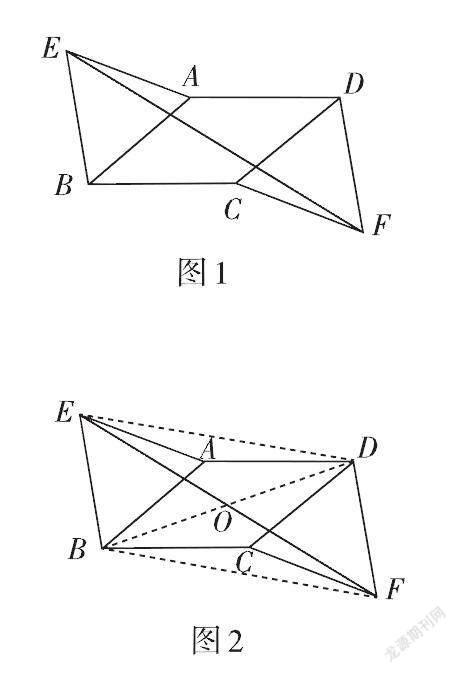
例 如图1,在▱ABCD中,以AB,CD为边在▱ABCD外侧作等边三角形AEB和等边三角形CFD.求证:四边形EBFD是平行四边形.
学法指导1:从边的角度证明平行四边形,兼顾边的数量和位置关系,根据“一组对边平行且相等的四边形是平行四边形”求证结论.
证法1:如图2,连接ED,BF,BD,BD与EF交于点O,
∵四边形ABCD为平行四边形,
∴AB = CD,AB[⫽]CD,∴∠ABD = ∠CDB.
∵△AEB,△CFD均为等边三角形,
∴BE = AB = CD = DF,∠EBA = ∠CDF = 60°,
∴∠ABD + ∠EBA = ∠CDB + ∠CDF,即∠EBO = ∠FDO,
∴BE[⫽]DF.
∵BE[⫽]DF,BE = DF,∴四边形EBFD是平行四边形.
学法指导2:从边的角度证明平行四边形,如果只考虑边的数量关系,需要根据“两组对边分别相等”求证结论.
证法2:如图3,设AB,CD与EF分别交于点G,H,连接ED,BF,
∵四边形ABCD为平行四边形,
∴AB[⫽]CD,AB = CD,∴∠AGH = ∠CHG.
∵∠BGE = ∠AGH,∠DHF = ∠CHG,
∴∠BGE = ∠DHF.
∵△AEB,△CFD均為等边三角形,
∴BE = AB = CD = DF,∠EBA = ∠CDF = 60°.
∵∠BEG = 180° - ∠EBA - ∠BGE,∠DFH = 180° - ∠CDF - ∠DHF,
∴∠BEG = ∠DFH,∴BE[⫽]DF.
∵BE = DF,∴四边形EBFD是平行四边形.
学法指导3:从边的角度证明平行四边形,如果只考虑边的位置关系,需要根据“两组对边分别平行”来证明.
证法3:连接DE,BF,
∵四边形ABCD为平行四边形,
∴AD = BC,AD[⫽]BC,∠BAD = ∠BCD.
∵△AEB,△CFD均为等边三角形,
∴BE = AE = AB = CD = CF = DF,∠EAB = ∠DCF = 60°.
∵∠EAD = 360° - ∠EAB - ∠BAD,∠FCB = 360° - ∠DCF - ∠BCD,
∴∠EAD = ∠FCB.
∵AE = CF,AD = BC,∴△ADE ≌ △CBF,∴DE = BF.
∵BE = DF,DE = BF,∴四边形EBFD是平行四边形.
学法指导4:从特殊线的角度证明平行四边形,需要根据“对角线互相平分的四边形是平行四边形”来证明.
思考:你能类比上面的推理思路和过程,得到其他证法吗?你认为哪种证明思路更简捷?
分层作业
难度系数:★★★ 解题时间:4分钟
四边形ABCD为平行四边形,连接AC,点E,F在AC上,且AE = CF,求证:四边形DEBF为平行四边形.(请同学们从多角度思考,答案略)
〔作者单位:辽宁省实验中学(初中部)〕

